A Mechanikai Energia Fogalma: Átfogó Értelmezés és Alkalmazások

A mechanikai energia alapvető fogalom a fizikában és a mérnöki tudományokban, amely egy test vagy rendszer azon képességét írja le, hogy munkát végezzen a mozgásának vagy a helyzetének köszönhetően. Ez az energiaforma szorosan kapcsolódik a makroszkopikus objektumok mozgásához és kölcsönhatásaihoz, szemben például a termikus vagy elektromágneses energiával, amelyek a mikroszkopikus részecskék viselkedésével függnek össze. A mechanikai energia megértése kulcsfontosságú a fizikai jelenségek széles körének magyarázatához, a legegyszerűbb mozgásoktól kezdve a komplex gépek működéséig.

A Mechanikai Energia Két Fő Típusa

A mechanikai energiát alapvetően két fő összetevőre bonthatjuk: a kinetikus energiára és a potenciális energiára. Ezek az energiaformák szorosan összefüggenek, és egy mechanikai rendszer teljes energiája gyakran e kettő összegéből adódik.

A Kinetikus Energia: A Mozgás Energiája

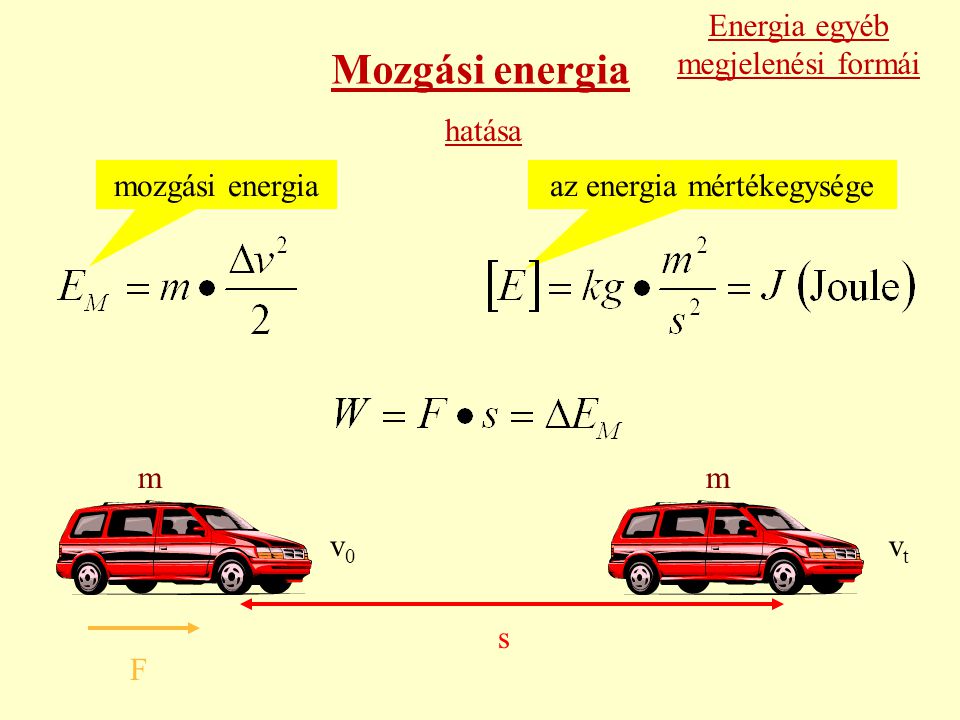
A kinetikus energia egy test mozgásából származó energia. Minél nagyobb egy test tömege és minél nagyobb a sebessége, annál nagyobb a kinetikus energiája. Matematikailag a kinetikus energia ($E_k$) a következőképpen fejezhető ki:

$$\mathbf{E_k = \frac{1}{2}mv^2}$$

ahol $m$ a test tömege, $v$ pedig a sebessége.

Példák a Kinetikus Energiára a Mindennapi Életben

• Egy száguldó autó jelentős kinetikus energiával rendelkezik.
• Egy repülő labda szintén kinetikus energiával bír.
• A szél, mint mozgó levegő, képes munkát végezni a kinetikus energiájának köszönhetően (pl. szélmalmok forgatása).
• Egy folyó víz kinetikus energiája vízierőművekben hasznosítható.

A Kinetikus Energia Szerepe a Technikában

A kinetikus energia számos technológiai alkalmazás alapját képezi. Például a turbinák forgása, a járművek mozgása, és a különféle gépek működése mind a kinetikus energián alapulnak. A mérnökök gyakran törekednek a kinetikus energia hatékony átalakítására más energiaformákká, vagy éppen a mozgás létrehozására más energiaformákból.

A Potenciális Energia: A Helyzetből vagy Konfigurációból Származó Energia

A potenciális energia egy test vagy rendszer azon energiája, amely a helyzetéből vagy a konfigurációjából adódik. Számos formája létezik, attól függően, hogy milyen erőhatás áll a háttérben. A leggyakrabban említett típusok a gravitációs potenciális energia és a rugalmas potenciális energia.

Gravitációs Potenciális Energia

A gravitációs potenciális energia egy test azon energiája, amely a gravitációs térben elfoglalt helyzetéből adódik. Egy $h$ magasságban lévő, $m$ tömegű test gravitációs potenciális energiája ($E_p$) a következőképpen számítható ki a Föld felszínéhez képest:

$$\mathbf{E_p = mgh}$$

ahol $g$ a gravitációs gyorsulás.

Példák a Gravitációs Potenciális Energiára

• Egy hegy tetején lévő kő nagyobb gravitációs potenciális energiával rendelkezik, mint egy a völgyben lévő.
• Egy megfeszített íjban lévő nyíl rendelkezik gravitációs potenciális energiával, ha függőlegesen tartjuk.
• A víztározókban felgyülemlett víz jelentős gravitációs potenciális energiával rendelkezik, amelyet vízierőművek hasznosítanak.

Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmasan deformált testben tárolt energia. Ha egy rugót megnyújtunk vagy összenyomunk, munkát végzünk rajta, és ez a munka rugalmas potenciális energia formájában tárolódik. A rugalmas potenciális energia ($E_{rug}$) egy $x$-szel megnyújtott vagy összenyomott ideális rugó esetén a következőképpen adható meg:

$$\mathbf{E_{rug} = \frac{1}{2}kx^2}$$

ahol $k$ a rugóállandó, $x$ pedig a rugó egyensúlyi helyzetétől való elmozdulása.

Példák a Rugalmas Potenciális Energiára

• Egy összenyomott rugó rugalmas potenciális energiával rendelkezik.
• Egy megfeszített gumiszalagban szintén rugalmas potenciális energia tárolódik.
• A trambulinra ugró ember a trambulin rugalmas deformációja révén rugalmas potenciális energiát halmoz fel.

Egyéb Formái a Potenciális Energiának

Bár a gravitációs és a rugalmas potenciális energia a leggyakrabban tárgyaltak, léteznek más formái is, mint például az elektromos potenciális energia (két elektromos töltés relatív helyzetéből adódó energia) és a mágneses potenciális energia (mágneses mezőben lévő mágneses dipólus energiája).

A Mechanikai Energia Megmaradásának Törvénye

A mechanikai energia megmaradásának törvénye az egyik legalapvetőbb elv a fizikában. Kimondja, hogy egy izolált rendszerben, ahol csak konzervatív erők (mint a gravitációs erő és az ideális rugóerő) hatnak, a mechanikai energia (a kinetikus és a potenciális energia összege) állandó marad. Matematikailag:

$$\mathbf{E_{mechanikai} = E_k + E_p = állandó}$$

Konzervatív és Nemkonzervatív Erők

A mechanikai energia megmaradása csak akkor érvényes, ha a rendszerben csak konzervatív erők hatnak. Egy erő akkor konzervatív, ha az általa végzett munka nem függ a megtett úttól, csak a kezdeti és a végső ponttól. A gravitációs erő és az ideális rugóerő példák konzervatív erőkre. Ezzel szemben a súrlódási erő egy nemkonzervatív erő, mert az általa végzett munka függ a megtett úttól, és a mechanikai energia egy része hővé alakul.

Példák a Mechanikai Energia Megmaradására

• Egy ingamozgása során a potenciális energia folyamatosan kinetikus energiává alakul át a legalacsonyabb ponton, majd vissza potenciális energiává a szélső pontokon. Ideális esetben (súrlódás nélkül) a teljes mechanikai energia megmarad.
• Egy leeső test gravitációs potenciális energiája fokozatosan kinetikus energiává alakul át, miközben a teljes mechanikai energia állandó marad (légellenállástól eltekintve).
• Egy rugóra akasztott test oszcillációja során a rugalmas potenciális energia és a kinetikus energia periodikusan átalakulnak egymásba, miközben a rendszer teljes mechanikai energiája megmarad.

A Mechanikai Energia Átalakulásai

A valóságban ritkán találkozunk tökéletesen izolált rendszerekkel, és gyakran nemkonzervatív erők is hatnak. Ilyen esetekben a mechanikai energia nem marad meg teljesen, hanem más energiaformákká alakulhat át, például hővé (a súrlódás miatt). Azonban az energia megmaradásának általános törvénye továbbra is érvényes: az energia nem vész el és nem keletkezik a semmiből, csak átalakul egyik formából a másikba.

Példák a Mechanikai Energia Átalakulására

• Egy fékező autóban a kinetikus energia a fékek súrlódása révén hővé alakul.
• Egy vízierőműben a víz gravitációs potenciális energiája először kinetikus energiává alakul a turbinák forgatásával, majd ez a kinetikus energia elektromos energiává alakul a generátorban.
• Egy égő gyufa kémiai energiát alakít át hővé és fényenergiává, de a súrlódással meggyújtott gyufa esetében a mozgás kinetikus energiája hővé alakul, ami beindítja a kémiai reakciót.

A Mechanikai Energia Szerepe a Technikában és a Mérnökségben

A mechanikai energia megértése és alkalmazása központi szerepet játszik a mérnöki tervezésben és a technológiai fejlesztésekben. Számos gép és eszköz működése a mechanikai energia különböző formáinak átalakításán és hasznosításán alapul.

Gépészet és Mechanikai Energia

A gépészet egyik fő területe a gépek tervezése, gyártása és működtetése, amelyek gyakran a mechanikai energiát használják fel munka végzésére. Ide tartoznak a motorok (amelyek kémiai vagy elektromos energiát alakítanak át mechanikai energiává), a hajtóművek (amelyek a mechanikai energia átvitelét és módosítását végzik), és a különféle munkagépek (amelyek a mechanikai energiát valamilyen hasznos feladatra fordítják).

Építőmérnökség és Mechanikai Energia

Az építőmérnököknek is figyelembe kell venniük a mechanikai energiával kapcsolatos jelenségeket, például a szél terhelését az épületekre (ami kinetikus energiával függ össze), vagy a földrengések hatásait (amelyek a föld mozgásából származó mechanikai energiát jelentik).

Energiatermelés és Mechanikai Energia

Számos energiatermelési módszer a mechanikai energia valamilyen formájának elektromos energiává alakításán alapul. A vízierőművek a víz gravitációs potenciális energiáját és kinetikus energiáját hasznosítják, a szélenergia a szél kinetikus energiáját, a hőerőművek pedig a gőz kinetikus energiáját forgatják meg a turbinákat.

Összefoglalás: A Mechanikai Energia Jelentősége

A mechanikai energia a fizika és a mérnöki tudományok egyik alapvető fogalma, amely a testek mozgásával és helyzetével kapcsolatos munkavégző képességét írja le. Két fő formája a kinetikus energia (a mozgás energiája) és a potenciális energia (a helyzetből vagy konfigurációból származó energia). A mechanikai energia megmaradásának törvénye alapvető elv a zárt rendszerekben, ahol csak konzervatív erők hatnak. A valóságban az energia gyakran átalakul más formákká, de az energia megmaradásának általános törvénye mindig érvényesül. A mechanikai energia megértése és alkalmazása nélkülözhetetlen a technológia és a mérnökség számos területén.

További Kapcsolódó Fogalmak

• Munka
• Teljesítmény
• Energiaátalakítás
• Hatásfok

Reméljük, hogy ez az átfogó cikk segített megérteni a mechanikai energia fogalmát és annak jelentőségét a természeti és a technikai világban. Ha további kérdései vannak, ne habozzon felvenni velünk a kapcsolatot!