A Mechanikai Energia Megmaradásának Törvénye: A Fizika Egyik Alapköve

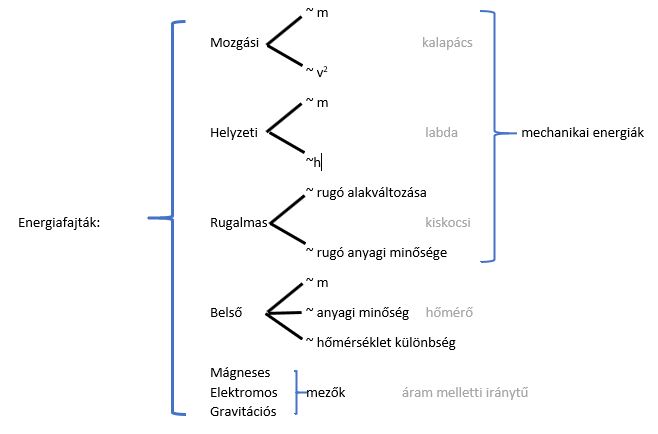
A mechanikai energia megmaradásának törvénye a fizika egyik legfontosabb és legszélesebb körben alkalmazható alapelve. Kimondja, hogy egy izolált rendszerben, ahol csak konzervatív erők (mint például a gravitációs erő vagy a rugalmas erő) hatnak, a mechanikai energia – vagyis a kinetikus energia és a potenciális energia összege – időben állandó marad. Ez azt jelenti, hogy az energia nem vész el, hanem csak átalakul egyik formájából a másikba. Ebben a részletes cikkben mélyrehatóan megvizsgáljuk ezt a fundamentális törvényt, feltárjuk a mögötte rejlő elveket, szemléletes példákon keresztül mutatjuk be alkalmazásait, és megvitatjuk a nem konzervatív erők hatását is.

A Mechanikai Energia Definíciója és Összetevői

A mechanikai energia egy rendszer azon képessége, hogy munkát végezzen a mozgása vagy a helyzete miatt. Két fő összetevője van: a kinetikus energia és a potenciális energia. Ahhoz, hogy teljes mértékben megértsük a mechanikai energia megmaradásának törvényét, elengedhetetlen, hogy tisztában legyünk ezen összetevők definíciójával és jelentésével.

A Kinetikus Energia: A Mozgás Energiája

A kinetikus energia egy test mozgásából származó energia. Minél nagyobb egy test tömege és minél gyorsabban mozog, annál nagyobb a kinetikus energiája. Matematikailag a kinetikus energia (E\_k) a következőképpen fejezhető ki:

\\mathbf\{E\_k \= \\frac\{1\}\{2\}mv^2\}

ahol \\mathbf\{m\} a test tömege, \\mathbf\{v\} pedig a sebessége. Ebből az egyenletből is látható, hogy a kinetikus energia négyzetesen függ a sebességtől, ami azt jelenti, hogy a sebesség kétszeresére növelése négyszeresére növeli a kinetikus energiát. A tömeggel pedig egyenesen arányos, tehát kétszer akkora tömeg kétszer akkora kinetikus energiát jelent azonos sebesség mellett.

Gondoljunk csak egy guruló labdára, egy repülő repülőgépre vagy egy futó emberre. Mindegyik rendelkezik kinetikus energiával a mozgásuk miatt. Minél gyorsabban mozognak, annál nagyobb ez az energia. A kinetikus energia kulcsszerepet játszik számos fizikai jelenség megértésében, a mikroszkopikus részecskék mozgásától kezdve a bolygók pályájáig.

A Potenciális Energia: A Helyzetből Származó Energia

A potenciális energia egy test helyzetéből vagy konfigurációjából származó tárolt energia. Többféle formája létezik, attól függően, hogy milyen erőhatás eredményezi ezt az energiát. A mechanikában leggyakrabban a gravitációs potenciális energiával és a rugalmas potenciális energiával találkozunk.

Gravitációs Potenciális Energia

A gravitációs potenciális energia egy testnek a gravitációs térben elfoglalt helyzetéből adódik. A Föld felszínén, egy \\mathbf\{h\} magasságban lévő \\mathbf\{m\} tömegű test gravitációs potenciális energiája (E\_p) a következőképpen számítható ki:

\\mathbf\{E\_p \= mgh\}

ahol \\mathbf\{g\} a gravitációs gyorsulás (a Földön megközelítőleg 9\.81 \\, m/s^2). Ebből az egyenletből láthatjuk, hogy minél magasabbra emelünk egy testet, annál nagyobb lesz a gravitációs potenciális energiája. Ez az energia akkor szabadul fel, amikor a test leesik, és a potenciális energia kinetikus energiává alakul át.

Például egy hegy tetején álló kő nagyobb gravitációs potenciális energiával rendelkezik, mint egy a völgyben fekvő kő. Amikor a kő legurul a hegyről, ez a potenciális energia fokozatosan kinetikus energiává alakul át, miközben a magassága csökken.

Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmasan deformálható testben (például egy megnyújtott rugóban vagy egy meghajlított íjban) tárolt energia. Ha egy rugót \\mathbf\{x\} távolsággal megnyújtunk vagy összenyomunk a nyugalmi helyzetéhez képest, a benne tárolt rugalmas potenciális energia (E\_\{pr\}) a következőképpen adható meg:

\\mathbf\{E\_\{pr\} \= \\frac\{1\}\{2\}kx^2\}

ahol \\mathbf\{k\} a rugóállandó, amely a rugó merevségét jellemzi. Minél nagyobb a rugóállandó vagy a deformáció mértéke, annál nagyobb a tárolt rugalmas potenciális energia.

Egy megfeszített íjban tárolt rugalmas potenciális energia például arra használható fel, hogy egy nyilat nagy sebességgel kilőjön. Amikor az íj elengedik, a rugalmas potenciális energia kinetikus energiává alakul át, ami a nyilat repíti.

A Mechanikai Energia Megmaradásának Törvénye: A Kimondás és Magyarázat

Most, hogy megértettük a kinetikus és a potenciális energia fogalmát, rátérhetünk a mechanikai energia megmaradásának törvényére. Ahogy korábban említettük, ez a törvény azt állítja, hogy egy olyan izolált rendszerben, amelyre csak konzervatív erők hatnak, a mechanikai energia (a kinetikus és potenciális energia összege) állandó marad.

Matematikailag ezt a következőképpen fejezhetjük ki:

\\mathbf\{E\_\{mech\} \= E\_k \+ E\_p \= állandó\}

Vagyis, ha egy rendszer kezdeti állapotában a kinetikus energia E\_\{k1\} és a potenciális energia E\_\{p1\}, a mechanikai energia E\_\{mech1\} \= E\_\{k1\} \+ E\_\{p1\}. Egy későbbi időpontban, ha a kinetikus energia E\_\{k2\} és a potenciális energia E\_\{p2\}, akkor a mechanikai energia E\_\{mech2\} \= E\_\{k2\} \+ E\_\{p2\}. A megmaradás törvénye szerint:

\\mathbf\{E\_\{mech1\} \= E\_\{mech2\}\}

\\mathbf\{E\_\{k1\} \+ E\_\{p1\} \= E\_\{k2\} \+ E\_\{p2\}\}

Ez az egyenlet rendkívül hasznos problémák megoldásában, ahol energiatranszformációk történnek, de nincsenek nem konzervatív erők, amelyek energiát vonhatnak el a rendszerből (például súrlódás vagy légellenállás).

Konzervatív Erők vs. Nem Konzervatív Erők

A mechanikai energia megmaradásának törvénye szigorúan csak olyan rendszerekre érvényes, ahol a ható erők konzervatívak. Fontos megérteni a különbséget a konzervatív és a nem konzervatív erők között.

Konzervatív Erők

Egy erő akkor konzervatív, ha az általa végzett munka egy zárt úton nulla, vagy ha a két pont közötti munka független az úttól. A mechanikában a leggyakoribb konzervatív erők a gravitációs erő és a rugalmas erő. Amikor egy konzervatív erő munkát végez egy rendszeren, az energia potenciális energiaként tárolódik, és később visszanyerhető kinetikus energiaként (vagy más formában).

• Gravitációs erő: A gravitációs erő által végzett munka egy test felemelésekor megegyezik a gravitációs potenciális energia növekedésével. Amikor a test leesik, ez a potenciális energia kinetikus energiává alakul vissza.
• Rugalmas erő: Egy rugó megnyújtásakor vagy összenyomásakor a rugalmas erő munkát végez, amely rugalmas potenciális energiaként tárolódik. Amikor a rugó visszatér nyugalmi helyzetébe, ez az energia kinetikus energiává alakulhat.

Nem Konzervatív Erők

Egy erő akkor nem konzervatív, ha az általa végzett munka függ az úttól, és nem nulla egy zárt úton. A mechanikában a leggyakoribb nem konzervatív erők a súrlódási erő és a légellenállás. Amikor egy nem konzervatív erő munkát végez, az energia általában hővé alakul, és nem tér vissza a rendszer mechanikai energiájába.

• Súrlódási erő: Ha egy test egy felületen csúszik, a súrlódási erő munkát végez, amely hővé alakítja a mechanikai energiát (mind a test, mind a felület felmelegszik). Ez az energia nem nyerhető vissza mechanikai munkaként a rendszerben.
• Légellenállás: Egy levegőben mozgó testre ható légellenállási erő szintén nem konzervatív. Munkája hővé alakítja a mechanikai energiát és a levegő áramlásának energiájává.

A mechanikai energia megmaradásának törvénye csak akkor alkalmazható közvetlenül, ha a rendszerben ható összes erő konzervatív. Ha nem konzervatív erők is jelen vannak, akkor a rendszer teljes energiája (beleértve a hőenergiát is) marad meg, de a mechanikai energia önmagában nem feltétlenül állandó.

Példák a Mechanikai Energia Megmaradására

Számos klasszikus példa illusztrálja a mechanikai energia megmaradásának törvényét a gyakorlatban. Nézzünk meg néhányat részletesen:

Egy Szabadon Eső Test

Képzeljünk el egy \\mathbf\{m\} tömegű testet, amelyet egy \\mathbf\{h\} magasságból elejtünk. Kezdetben a test nyugalomban van, így a kinetikus energiája nulla (E\_\{k1\} \= 0), a potenciális energiája pedig E\_\{p1\} \= mgh. Tehát a kezdeti mechanikai energia E\_\{mech1\} \= 0 \+ mgh \= mgh.

Amint a test esni kezd, a gravitációs erő munkát végez rajta, és a potenciális energiája csökken, miközben a sebessége és ezzel együtt a kinetikus energiája nő. Egy tetszőleges \\mathbf\{y\} magasságban (ahol 0 \\le y \\le h), a potenciális energia E\_\{p2\} \= mgy. A sebességet ebben a pontban a következőképpen számíthatjuk ki a mozgásegyenletekből:

v^2 \= v\_0^2 \+ 2a\(h\-y\)

Mivel a kezdeti sebesség v\_0 \= 0 és a gyorsulás a \= g, ezért:

v^2 \= 2g\(h\-y\)

Így a kinetikus energia ebben a pontban:

E\_\{k2\} \= \\frac\{1\}\{2\}mv^2 \= \\frac\{1\}\{2\}m\(2g\(h\-y\)\) \= mg\(h\-y\)

A mechanikai energia ezen a ponton tehát:

E\_\{mech2\} \= E\_\{k2\} \+ E\_\{p2\} \= mg\(h\-y\) \+ mgy \= mgh

Láthatjuk, hogy E\_\{mech1\} \= E\_\{mech2\} \= mgh, ami azt bizonyítja, hogy a mechanikai energia megmarad a szabadesés során (feltételezve, hogy a légellenállás elhanyagolható).

A földetérés pillanatában (y \= 0), a potenciális energia nulla (E\_\{p3\} \= 0), a kinetikus energia pedig:

E\_\{k3\} \= mg\(h\-0\) \= mgh

Így a mechanikai energia ekkor is E\_\{mech3\} \= mgh \+ 0 \= mgh. Az egész folyamat során a gravitációs potenciális energia folyamatosan kinetikus energiává alakul át, de a kettő összege (a mechanikai energia) állandó marad.

Egy Ideális Ingamozgása

Tekintsünk egy ideális ingát, amely egy \\mathbf\{L\} hosszúságú, súlytalan fonálon függő \\mathbf\{m\} tömegű testből áll, és súrlódás nélkül leng. Amikor az inga a legmagasabb pontján van (valamelyik szélső helyzetben), pillanatnyi sebessége nulla, így a kinetikus energiája is nulla. Ebben a pontban a gravitációs potenciális energiája maximális, a legalacsonyabb ponthoz (egyensúlyi helyzethez) viszonyít