Az Ellenállás Mértékegysége: Átfogó Leitfaden az Ohm Világában

Az elektromosság világában az ellenállás alapvető fogalom, amely meghatározza, hogy egy anyag mennyire akadályozza az elektromos áram áramlását. Ennek a tulajdonságnak a számszerűsítésére egy speciális mértékegységet használunk, az ohmot. Ebben a részletes útmutatóban mélyrehatóan feltárjuk az ohm jelentőségét, történetét, definícióit és gyakorlati alkalmazásait, hogy Ön teljes mértékben megértse ezt a kulcsfontosságú fizikai mennyiséget.

Az Ohm Története: Georg Simon Ohm Öröksége

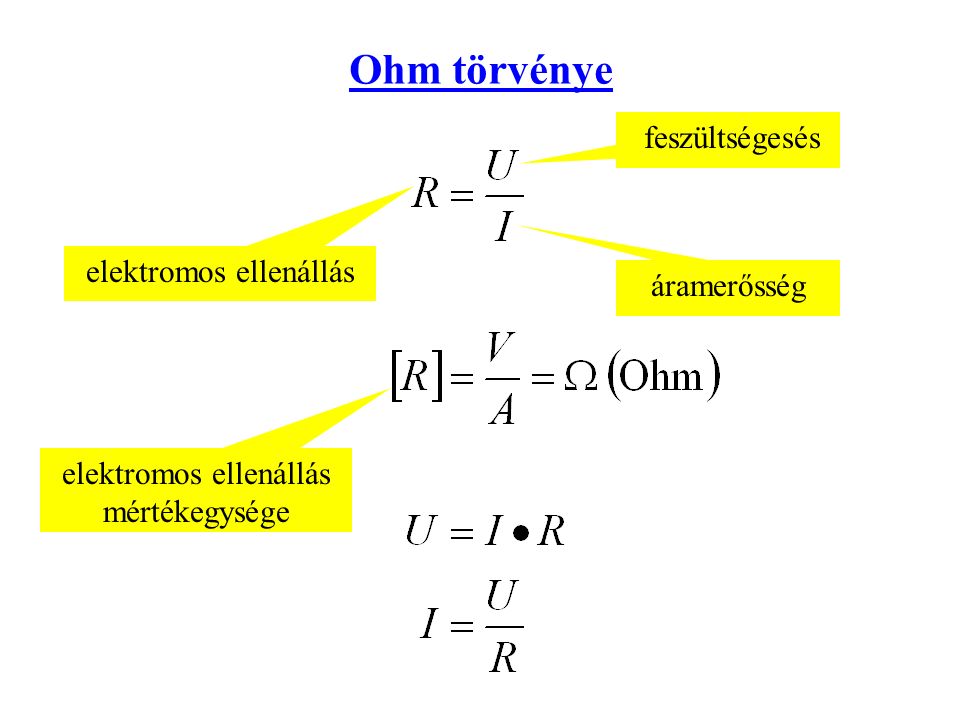
Az ellenállás mértékegysége a német fizikus, Georg Simon Ohm tiszteletére kapta a nevét. Ohm a 19. század elején végzett úttörő kísérleteket az elektromos áram és a feszültség közötti kapcsolatra vonatkozóan. 1827-ben publikálta híres törvényét, az Ohm törvényét, amely kimondja, hogy egy vezetőn átfolyó áram egyenesen arányos a vezető két vége közötti feszültséggel, és fordítottan arányos a vezető ellenállásával. Ez a felfedezés forradalmasította az elektromosság megértését, és megalapozta az elektromos áramkörök tervezését és analízisét.

Georg Simon Ohm Élete és Munkássága

Georg Simon Ohm 1789-ben született Erlangenben. Matematikai és fizikai tanulmányai után különböző tanári állásokat töltött be. Kísérleteit kezdetben saját maga által készített egyszerű eszközökkel végezte. Gondos mérései és analízisei vezettek az Ohm törvényének megfogalmazásához, amely először nem aratott osztatlan sikert a tudományos közösségben. Azonban munkájának jelentőségét később elismerték, és az ő tiszteletére nevezték el az ellenállás mértékegységét ohm-nak.

Az Ohm Törvényének Megszületése

Ohm kísérletei során különböző anyagokból készült vezetőkön vizsgálta az áram és a feszültség közötti kapcsolatot. Megállapította, hogy bizonyos anyagok esetében ez a kapcsolat lineáris, ami azt jelenti, hogy ha megduplázzuk a feszültséget, az áram is megduplázódik. Ezt a lineáris kapcsolatot fejezi ki az Ohm törvénye, amelynek matematikai formája a következő:

$$\mathbf{V = IR}$$

ahol:

• $\mathbf{V}$ a feszültség (voltokban mérve)
• $\mathbf{I}$ az áram (amperben mérve)
• $\mathbf{R}$ az ellenállás (ohmban mérve)

Ez az egyszerű, de rendkívül hatékony egyenlet az elektromos áramkörök alapköve lett.

Az Ohm Definíciója és Jelölése

Az ohm az elektromos ellenállás SI-mértékegysége. A definíció szerint egy ohm az az ellenállás, amelyen egy volt feszültség hatására egy amper áram folyik keresztül.

Az Ohm Szimbóluma

Az ohm mértékegység szimbóluma a görög nagy omega betű: $\mathbf{\Omega}$. Tehát, ha azt látjuk, hogy egy alkatrész ellenállása 10 $\Omega$, az azt jelenti, hogy az adott alkatrész 10 ohm ellenállást fejt ki az árammal szemben.

Az Ohm Nemzetközi Definíciója

A Nemzetközi Mértékegységrendszer (SI) pontosan definiálja az ohmot a többi alapvető mértékegységgel való kapcsolatán keresztül. Bár a korábbi definíciók fizikai megvalósításokon alapultak, a jelenlegi definíció a kvantummechanikai hatásokon, nevezetesen a kvantált Hall-ellenálláson alapul, ami rendkívül pontos és reprodukálható mértékegységet biztosít.

Az Ellenállás Fogalmának Mélyebb Értelmezése

Az ellenállás egy anyagnak az a tulajdonsága, hogy gátolja az elektromos áram áramlását. Ezt a gátlást az anyag atomjainak és molekuláinak belső szerkezete okozza. Amikor elektromos mező hatására a töltött részecskék (általában elektronok) mozogni kezdenek egy anyagban, ütköznek az anyag atomjaival. Ezek az ütközések energiát disszipálnak, ami hő formájában jelentkezik, és egyben csökkentik az elektronok sebességét, ezáltal létrehozva az ellenállást.

Vezetők, Szigetelők és Félvezetők Ellenállása

Az anyagok elektromos vezetőképességük szempontjából három fő csoportba sorolhatók:

• Vezetők: Ezek az anyagok, mint például a réz és az alumínium, alacsony ellenállással rendelkeznek, ami azt jelenti, hogy könnyen áram folyik át rajtuk. Belső szerkezetükben sok szabad elektron található, amelyek könnyen mozoghatnak.
• Szigetelők: Az olyan anyagok, mint a gumi és az üveg, nagyon magas ellenállással rendelkeznek, ami megakadályozza az áram áramlását. Kevés szabad elektronjuk van, és az elektronok erősen kötődnek az atommagokhoz.
• Félvezetők: Ezek az anyagok, mint például a szilícium és a germánium, vezetőképessége a vezetők és a szigetelők között van. Vezetőképességük külső tényezőkkel, például hőmérséklettel vagy szennyezéssel (doppingolással) szabályozható.

Az Ellenállást Befolyásoló Tényezők

Egy adott vezető ellenállását több tényező is befolyásolja:

• Az anyag fajtája: Különböző anyagok különböző atomi szerkezettel rendelkeznek, ami eltérő mértékű ellenállást eredményez. Ezt a tulajdonságot fajlagos ellenállásnak ($\mathbf{\rho}$) nevezzük, amely az anyagra jellemző állandó.
• A vezető hossza (l): Minél hosszabb egy vezető, annál nagyobb az ellenállása, mivel az elektronoknak hosszabb utat kell megtenniük, és így több atommal ütköznek. Az ellenállás egyenesen arányos a hosszal.
• A vezető keresztmetszete (A): Minél nagyobb a vezető keresztmetszete, annál kisebb az ellenállása, mivel több hely áll rendelkezésre az elektronok áramlásához. Az ellenállás fordítottan arányos a keresztmetszettel.

• A hőmérséklet (T): A legtöbb fém esetében a hőmérséklet növekedésével az ellenállás is nő, mivel a megnövekedett hőmozgás több ütközést okoz az elektronok és az atomok között. Félvezetők esetében a helyzet bonyolultabb lehet.

Az Ellenállás Kiszámítása

Egy homogén anyagból készült, egyenletes keresztmetszetű vezető ellenállása a következőképpen számítható ki:

$$\mathbf{R = \rho \frac{l}{A}}$$

ahol:

• $\mathbf{R}$ az ellenállás (ohmban)
• $\mathbf{\rho}$ az anyag fajlagos ellenállása (ohm-méterben, $\Omega \cdot m$)
• $\mathbf{l}$ a vezető hossza (méterben, $m$)
• $\mathbf{A}$ a vezető keresztmetszete (négyzetméterben, $m^2$)

Ez az egyenlet alapvető fontosságú az elektromos áramkörök tervezésénél és az anyagok elektromos tulajdonságainak megértésénél.

Az Ohm Gyakorlati Alkalmazásai

Az ohm, mint az ellenállás mértékegysége, számtalan gyakorlati alkalmazással bír az elektromosság és az elektronika területén.

Ellenállások az Elektronikai Áramkörökben

Az ellenállások olyan elektronikai alkatrészek, amelyek meghatározott ellenállással rendelkeznek. Ezeket széles körben használják áramkörökben különböző célokra:

• Áramkorlátozás: Az ellenállásokkal beállítható az áram erőssége egy adott áramkörben.
• Feszültségosztás: Több ellenállás soros kapcsolásával a feszültség meghatározott arányban felosztható.
• Hőtermelés: Bizonyos alkalmazásokban az ellenállásokat hő előállítására használják (pl. fűtőelemek).
• Jelformálás: Az ellenállások kondenzátorokkal vagy induktorokkal kombinálva időállandókat hozhatnak létre, amelyek befolyásolják a jelek viselkedését.

Különböző Típusú Ellenállások

Számos különböző típusú ellenállás létezik, amelyek különböző alkalmazásokhoz készülnek:

• Szénréteg ellenállások: Olcsók és széles körben használatosak általános célokra.
• Fémréteg ellenállások: Pontosabbak és stabilabbak, mint a szénréteg ellenállások.
• Huzalellenállások: Nagyobb teljesítmény elviselésére alkalmasak.
• Potenciométerek: Változtatható ellenállású alkatrészek, amelyeket gyakran használnak hangerőszabályozásra vagy érzékelőként.
• Trimmerek: Kis méretű, beállítható ellenállások, amelyeket áramkörök finomhangolására használnak.

Az Ellenállás Mérése

Az ellenállás értékének mérésére különböző eszközök állnak rendelkezésre:

• Ohm-mérő: Egy olyan műszer, amelyet kifejezetten az ellenállás mérésére terveztek.
• Multiméter: Egy sokoldalú mérőműszer, amely képes feszültség, áram és ellenállás mérésére is.

Az ellenállás mérése gyakran az Ohm törvényén alapul: ha ismerjük a vezetőn átfolyó áramot és a rajta eső feszültséget, akkor az ellenállás kiszámítható a $\mathbf{R = V/I}$ képlettel.

Az Ellenállás és a Hőmérséklet Kapcsolata Részletesen

Mint korábban említettük, a hőmérséklet jelentős hatással lehet az anyagok ellenállására. A legtöbb fém esetében a hőmérséklet emelkedésével az ellenállás nő. Ennek oka, hogy a magasabb hőmérséklet fokozza az atomok rezgését a kristályrácsban. A szabad elektronok, miközben áthaladnak a vezetőn, gyakrabban ütköznek ezekkel a rezgő atomokkal, ami növeli az árammal szembeni akadályozást, vagyis az ellenállást.

A Hőmérsékleti Együttható

Az anyagok ellenállásának hőmérsékletfüggőségét a hőmérsékleti együtthatóval ($\mathbf{\alpha}$) fejezzük ki. Ez a tényező megadja, hogy az ellenállás egységnyi hőmérséklet-változás hatására mennyivel változik az eredeti ellenálláshoz képest. A hőmérséklet és az ellenállás közötti kapcsolat lineáris közelítésben a következőképpen írható le:

$$\mathbf{R(T) = R_0 [1 + \alpha (T – T_0)]}$$

ahol:

• $\mathbf{R(T)}$ az ellenállás $T$ hőmérsékleten
• $\mathbf{R_0}$ az ellenállás egy referencia hőmérsékleten ($T_0$, gyakran 20 °C)
• $\mathbf{\alpha}$ az anyag hőmérsékleti együtthatója (°C$^{ -1}$-ben vagy K$^{ -1}$-ben)
• $\mathbf{T}$ az aktuális hőmérséklet
• $\mathbf{T_0}$ a referencia hőmérséklet

Különböző anyagoknak eltérő a hőmérsékleti együtthatójuk. A fémek általában pozitív hőmérsékleti együtthatóval rendelkeznek (ellenállásuk nő a hőmérséklettel), míg egyes félvezetőknek negatív (ellenállásuk csökken a hőmérséklettel).

A Hőmérséklet Hatása a Félvezetőkre

A félvezetők esetében a hőmérséklet hatása bonyolultabb, mint a fémeknél. Alacsony hőmérsékleten a félvezetők szigetelőként viselkednek, mivel kevés szabad töltéshordozójuk van. A hőmérséklet növekedésével azonban egyre több elektron jut elegendő energiához ahhoz, hogy leküzdje a sávszélességet és vezetővé váljon. Ezért a félvezetők ellenállása általában csökken a hőmérséklet növekedésével, ami negatív hőmérsékleti együtthatót eredményez.

A Szupervezetés Jelensége

Bizonyos anyagok rendkívül alacsony hőmérsékleten elveszítik minden elektromos ellenállásukat. Ezt a jelenséget szupervezetésnek nevezzük. A szupervezetőkben az áram veszteség nélkül áramolhat. A szupervezetésnek számos potenciális alkalmazása van, például nagy hatékonyságú elektromos energiaátvitel, erős elektromágnesek és gyors elektronikai eszközök.

Az Ellenállás Kapcsolásai: Soros és Párhuzamos Kapcsolások

Az elektronikai áramkörökben az ellenállásokat gyakran kombinálják sorosan vagy párhuzamosan a kívánt eredő ellenállás elérése érdekében.

Soros Kapcsolás

Soros kapcsolás esetén az ellenállások egymás után vannak kötve, így az áramnak mindegyiken keresztül kell áthaladnia. A sorosan kapcsolt ellenállások eredő ellenállása ($\mathbf{R_{eredő}}$) az egyes ellenállások értékének összege:

$$\mathbf{R_{eredő} = R_1 + R_2 + R_3 + \dots + R_n}$$

Soros kapcsolásban az áram minden ellenálláson azonos, míg a feszültség az egyes ellenállásokon az értékükkel arányosan oszlik meg.

Párhuzamos Kapcsolás

Párhuzamos kapcsolás esetén az ellenállások egymás mellé