Ellenállás Bekötése: A Részletes Útmutató a Sikeres Áramkörökhöz

Az elektronika világában az ellenállások alapvető fontosságú alkatrészek, amelyek az áram folyását korlátozzák. Megfelelő bekötésük elengedhetetlen a biztonságos és hatékony áramkörök létrehozásához. Ebben a részletes útmutatóban lépésről lépésre végigvezetjük Önt az ellenállások különböző bekötési módjain, a színkódok értelmezésén, valamint gyakorlati tanácsokat adunk a sikeres áramkörök tervezéséhez és megépítéséhez.

Az Ellenállások Alapjai és Fontossága

Mielőtt belemerülnénk az ellenállások bekötésének rejtelmeibe, érdemes tisztáznunk, hogy mi is pontosan az ellenállás és miért olyan kulcsfontosságú az elektronikai áramkörökben. Az ellenállás egy olyan elektromos alkatrész, amely akadályozza az elektromos áram áramlását. Ezt az akadályozást ohmban ($\Omega$) mérjük. Az ellenállások nélkülözhetetlenek számos funkció ellátásához, beleértve az áram korlátozását, a feszültség osztását és a hőtermelést.

Miért Nélkülözhetetlenek az Ellenállások?

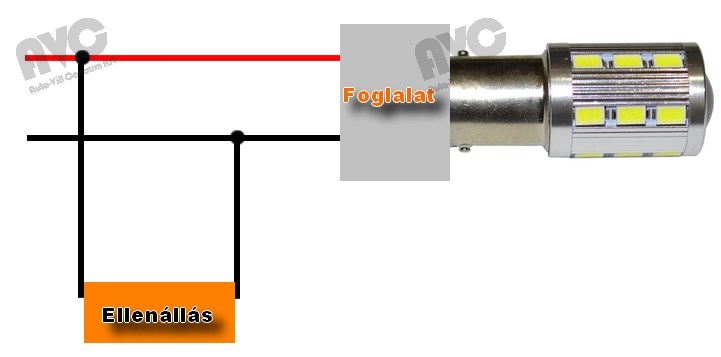
• Áramkorlátozás: Megvédik az érzékeny alkatrészeket a túlzott áramtól, ami károsodáshoz vezethet. Például egy LED elé kötött ellenállás megakadályozza, hogy a LED tönkremenjen a túl nagy áram miatt.
• Feszültségosztás: Lehetővé teszik, hogy egy adott feszültséget kisebb, meghatározott értékekre osszunk fel. Ez különösen hasznos olyan áramkörökben, ahol különböző feszültségszintekre van szükség.
• Jelgenerálás és -formálás: Bizonyos áramkörökben az ellenállások más alkatrészekkel (például kondenzátorokkal) kombinálva időzítő áramköröket vagy szűrőket hoznak létre.
• Hőtermelés: Egyes speciális esetekben az ellenállásokat szándékosan használják hőtermelésre, például fűtőelemekben.

Az Ellenállások Főbb Típusai

Számos különböző típusú ellenállás létezik, amelyek eltérő tulajdonságokkal és alkalmazási területekkel rendelkeznek. A leggyakoribb típusok közé tartoznak a szénréteg ellenállások, a fémréteg ellenállások és a huzaltekercselt ellenállások.

Szénréteg Ellenállások

A szénréteg ellenállások vékony szénrétegből készülnek egy kerámia vagy üvegrúdra felhordva. Általában olcsók és széles körben elterjedtek az általános célú alkalmazásokban. Toleranciájuk általában 5% vagy 10% körül van.

Fémréteg Ellenállások

A fémréteg ellenállások vékony fémrétegből (például nikkel-króm) készülnek. Pontosabbak, mint a szénréteg ellenállások, tipikusan 1% vagy 2% toleranciával rendelkeznek, és jobb a hőmérsékleti stabilitásuk. Ezért precízebb alkalmazásokhoz ideálisak.

Huzaltekercselt Ellenállások

A huzaltekercselt ellenállások egy szigetelő anyagra (például kerámiára) feltekercselt fémhuzalból állnak. Nagyobb teljesítmény leadására képesek, és alacsony az ellenállásuk. Főként tápegységekben és nagy áramú áramkörökben használják őket.

Egyéb Ellenállás Típusok

• SMD Ellenállások: Felületszerelt alkatrészek, amelyek kis méretük miatt modern elektronikai eszközökben elterjedtek.
• Potenciométerek: Változtatható ellenállású alkatrészek, amelyekkel az áramkör ellenállását manuálisan lehet állítani.
• Trimmerek: Kisebb, általában beállításra használt változtatható ellenállások.
• Termisztorok: Olyan ellenállások, amelyek ellenállása a hőmérséklettel változik.
• Varisztorok: Feszültségfüggő ellenállások, amelyek túlfeszültség elleni védelemre szolgálnak.

Az Ellenállások Értékének Meghatározása a Színkód Segítségével

A legtöbb hagyományos (nem SMD) ellenálláson színes sávok jelzik az ellenállás értékét, a toleranciáját és néha a hőmérsékleti együtthatóját. A színkód ismerete elengedhetetlen az ellenállások azonosításához.

A Négy Sávos Színkód

A leggyakoribb a négy sávos színkód. Az első két sáv az ellenállás értékének két szignifikáns számjegyét jelöli, a harmadik sáv a szorzót (tízes hatványát), a negyedik sáv pedig a toleranciát.

Szín	Érték	Szorzó	Tolerancia
Fekete	0	$10^0 = 1$	–
Barna	1	$10^1 = 10$	±1%
Vörös	2	$10^2 = 100$	±2%
Narancs	3	$10^3 = 1000$	–
Sárga	4	$10^4 = 10000$	–
Zöld	5	$10^5 = 100000$	±0.5%
Kék	6	$10^6 = 1000000$	±0.25%
Ibolya	7	$10^7 = 10000000$	±0.1%
Szürke	8	$10^8 = 100000000$	±0.05%
Fehér	9	$10^9 = 1000000000$	–
Arany	–	$10^{ -1} = 0.1$	±5%
Ezüst	–	$10^{ -2} = 0.01$	±10%

Példa: Egy ellenálláson a következő színek láthatók: barna, fekete, piros, arany.

• Barna (első sáv): 1
• Fekete (második sáv): 0
• Piros (harmadik sáv – szorzó): $10^2 = 100$
• Arany (negyedik sáv – tolerancia): ±5%

Az ellenállás értéke tehát $10 \times 100 = 1000 \Omega = 1 k\Omega$, ±5% tűréssel.

Az Öt Sávos Színkód

A precízebb ellenállásokon gyakran öt színes sáv található. Az első három sáv az ellenállás értékének három szignifikáns számjegyét jelöli, a negyedik sáv a szorzó, az ötödik sáv pedig a toleranciát.

Példa: Egy ellenálláson a következő színek láthatók: barna, fekete, fekete, piros, barna.

• Barna (első sáv): 1
• Fekete (második sáv): 0
• Fekete (harmadik sáv): 0
• Piros (negyedik sáv – szorzó): $10^2 = 100$
• Barna (ötödik sáv – tolerancia): ±1%

Az ellenállás értéke tehát $100 \times 100 = 10000 \Omega = 10 k\Omega$, ±1% tűréssel.

A Hat Sávos Színkód

A hat sávos színkód megegyezik az öt sávossal, de egy hatodik sávot is tartalmaz, amely a hőmérsékleti együtthatót jelöli ppm/K-ben (parts per million per Kelvin).

Szín	Hőmérsékleti Együttható (ppm/K)
Fekete	–
Barna	±100
Vörös	±50
Narancs	±15
Sárga	±25
Zöld	±20
Kék	±10
Ibolya	±5

Az Ellenállások Bekötésének Módjai

Az ellenállásokat többféleképpen lehet bekötni egy áramkörbe. A két alapvető mód a soros kapcsolás és a párhuzamos kapcsolás. Léteznek ezek kombinációi is.

Soros Kapcsolás

Soros kapcsolásban az ellenállások egymás után vannak kötve, így az áramnak ugyanazon az úton kell áthaladnia mindegyiken. A sorosan kötött ellenállások eredő ellenállása az egyes ellenállások értékeinek összege:

$$\mathbf{R_{eredő} = R_1 + R_2 + R_3 + … + R_n}$$

A Soros Kapcsolás Jellemzői

• Az áram minden ellenálláson azonos.
• A feszültség megoszlik az ellenállások között. Az egyes ellenállásokon eső feszültség arányos az ellenállás értékével (feszültségosztás).
• Az eredő ellenállás mindig nagyobb, mint a legnagyobb egyedi ellenállás értéke.

Példa Soros Kapcsolásra

Két ellenállást ($R_1 = 100 \Omega$ és $R_2 = 200 \Omega$) sorosan kötünk. Az eredő ellenállás:

$$R_{eredő} = 100 \Omega + 200 \Omega = 300 \Omega$$

Párhuzamos Kapcsolás

Párhuzamos kapcsolásban az ellenállások úgy vannak kötve, hogy mindegyikre ugyanaz a feszültség jut, de az áram megoszlik közöttük. A párhuzamosan kötött ellenállások eredő ellenállásának reciproka az egyes ellenállások reciprokösszege:

$$\mathbf{\frac{1}{R_{eredő}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + … + \frac{1}{R_n}}$$

Két ellenállás esetén a képlet egyszerűsíthető:

$$\mathbf{R_{eredő} = \frac{R_1 \times R_2}{R_1 + R_2}}$$

A Párhuzamos Kapcsolás Jellemzői

• A feszültség minden ellenálláson azonos.
• Az áram megoszlik az ellenállások között. Az egyes ellenállásokon átfolyó áram fordítottan arányos az ellenállás értékével (áramosztás).
• Az eredő ellenállás mindig kisebb, mint a legkisebb egyedi ellenállás értéke.

Példa Párhuzamos Kapcsolásra

Két ellenállást ($R_1 = 100 \Omega$ és $R_2 = 200 \Omega$) párhuzamosan kötünk. Az eredő ellenállás:

$$R_{eredő} = \frac{100 \Omega \times 200 \Omega}{100 \Omega + 200 \Omega} = \frac{20000}{300} \Omega \approx 66.67 \Omega$$

Kombinált Kapcsolások

Sok áramkörben az ellenállások soros és párhuzamos kapcsolások kombinációjaként vannak elrendezve. Az ilyen kombinált kapcsolások elemzéséhez először az egyszerűbb soros vagy párhuzamos részeket kell redukálni, amíg egyetlen eredő ellenállást nem kapunk.

Példa Kombinált Kapcsolásra

Tegyük fel, hogy van egy $R_1 = 50 \Omega$ ellenállás, amely sorosan van kötve egy párhuzamosan kapcsolt $R_2 = 100 \Omega$ és $R_3 = 150 \Omega$ ellenállás-párossal.

Először számítsuk ki a párhuzamos rész eredő ellenállását ($R_{23}$):

$$R_{23} = \frac{100 \Omega \times 150 \Omega}{100 \Omega + 150 \Omega} = \frac{15000}{250} \Omega = 60 \Omega$$

Most ez az eredő ellenállás ($R_{23}$) sorosan van kötve $R_1$-gyel, így a teljes eredő ellenállás ($R_{összes}$):

$$R_{összes} = R_1 + R_{23} = 50 \Omega + 60 \Omega = 110 \Omega$$

Gyakorlati Tudnivalók az Ellenállások Bekötéséhez

Az ellenállások fizikai bekötése során néhány fontos szempontot é