Ellenallas Ertekek
Az Ellenállás Értékek Részletes Világa: Útmutató Mérnököknek és Hobbi Elektronikusoknak
Az elektronika világában az ellenállás az egyik legalapvetőbb és legfontosabb passzív alkatrész. Az áramkörök működésének megértéséhez és tervezéséhez elengedhetetlen az ellenállás értékek ismerete és helyes alkalmazása. Ebben a részletes útmutatóban mélyrehatóan feltárjuk az ellenállásokkal kapcsolatos minden lényeges tudnivalót, a színkódok értelmezésétől a különböző kapcsolási módokon át a gyakorlati alkalmazásokig.
Az Ellenállás Fogalma és Jelentősége
Az ellenállás egy elektromos alkatrész azon tulajdonsága, amely akadályozza az elektromos áram áramlását. Mértékegysége az ohm ($\Omega$), amelyet Georg Simon Ohm német fizikus tiszteletére neveztek el. Az ellenállások kulcsszerepet játszanak az elektronikus áramkörökben az áram korlátozásában, a feszültség osztásában és a hő termelésében. Nélkülük a modern elektronika elképzelhetetlen lenne.
Az Ellenállás Szimbóluma az Áramkörökben
Az áramkörök sematikus rajzain az ellenállást általában egy cikk-cakk vonallal (amerikai szabvány) vagy egy téglalappal (európai szabvány) jelölik. Ez a szimbólum segít az áramkör felépítésének vizualizálásában és az egyes alkatrészek funkciójának megértésében.
Az Ellenállás Alapvető Funkciói
- Áramkorlátozás: Az ellenállások segítségével beállíthatjuk az áram erősségét egy adott áramkörben, megvédve ezzel más alkatrészeket a károsodástól.
- Feszültségosztás: Több ellenállás soros kapcsolásával a bemeneti feszültség arányosan osztható meg az egyes ellenállások között.
- Hőtermelés: Az áram áthaladásakor az ellenállások hőt termelnek (Joule-hő). Ezt a tulajdonságot fűtőelemekben és más hőtermelő eszközökben használják ki.
- Jelformálás: Bizonyos áramkörökben az ellenállások kondenzátorokkal vagy induktorokkal kombinálva időzítési állandók létrehozására és jelek formálására használhatók.
Az Ellenállás Értékének Meghatározása: A Színkódok Rendszere
A legtöbb hagyományos, kis teljesítményű ellenálláson színes sávok jelzik az ellenállás értékét és a tűrését. Ez a színkódos rendszer egy nemzetközileg elfogadott szabvány, amely lehetővé teszi az ellenállás értékének gyors és egyszerű azonosítását.

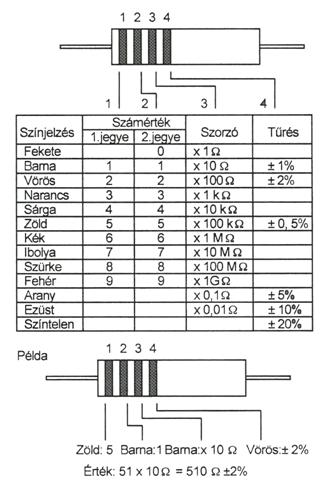
A Négy Sávos Színkód
A leggyakoribb típus a négy sávos ellenállás. A sávok jelentése a következő:
- Első sáv: Az ellenállás értékének első szignifikáns számjegye.
- Második sáv: Az ellenállás értékének második szignifikáns számjegye.
- Harmadik sáv: A szorzó, amely megmutatja, hogy az első két számjegyet hány tíz hatványával kell megszorozni.
- Negyedik sáv: A tűrés, amely az ellenállás névleges értékétől való maximális megengedett százalékos eltérést jelzi.
A Színkódok Táblázata
| Szín | Érték (1. & 2. sáv) | Szorzó (3. sáv) | Tűrés (4. sáv) |
|---|---|---|---|
| Fekete | 0 | $10^0 = 1$ | – |
| Barna | 1 | $10^1 = 10$ | ±1% |
| Vörös | 2 | $10^2 = 100$ | ±2% |
| Narancs | 3 | $10^3 = 1000$ | – |
| Sárga | 4 | $10^4 = 10000$ | – |
| Zöld | 5 | $10^5 = 100000$ | ±0.5% |
| Kék | 6 | $10^6 = 1000000$ | ±0.25% |
| Ibolya | 7 | $10^7 = 10000000$ | ±0.1% |
| Szürke | 8 | $10^8 = 100000000$ | ±0.05% |
| Fehér | 9 | $10^9 = 1000000000$ | – |
| Arany | – | $10^{ -1} = 0.1$ | ±5% |
| Ezüst | – | $10^{ -2} = 0.01$ | ±10% |
| Nincs szín | – | – | ±20% |
Például, ha egy ellenálláson a sávok sorrendje barna, fekete, piros és arany, akkor az értéke a következőképpen számítható ki:
- Barna (első sáv): 1
- Fekete (második sáv): 0
- Piros (harmadik sáv, szorzó): $10^2 = 100$
- Arany (negyedik sáv, tűrés): ±5%
Tehát az ellenállás értéke $10 \times 100 = 1000 \Omega = 1 k\Omega$, ±5% tűréssel.
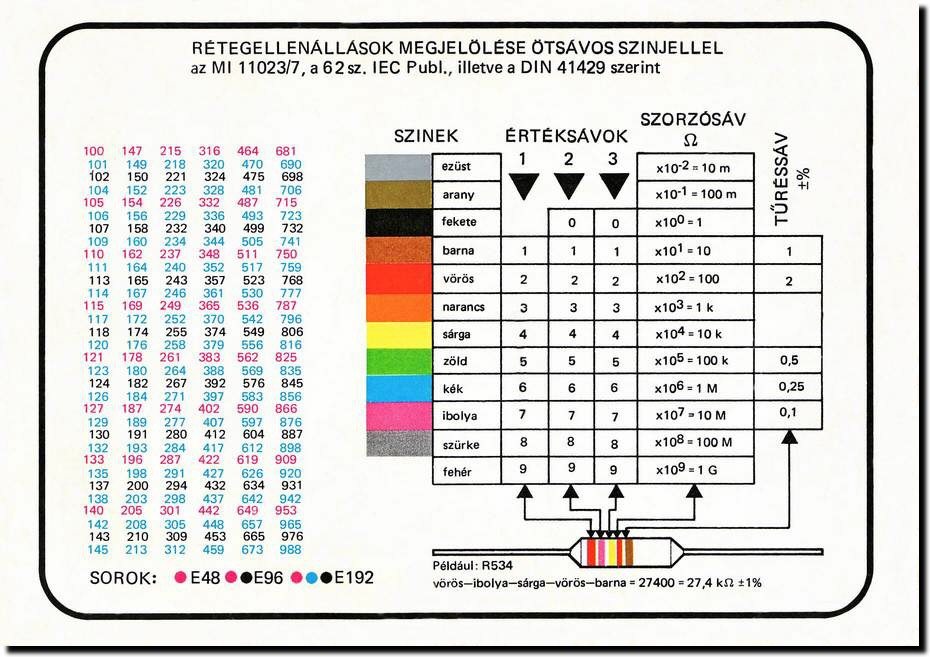
Az Öt Sávos Színkód
Nagyobb pontosságú ellenállásoknál gyakran öt színkódot alkalmaznak. Az öt sáv jelentése:
- Első sáv: Az ellenállás értékének első szignifikáns számjegye.
- Második sáv: Az ellenállás értékének második szignifikáns számjegye.
- Harmadik sáv: Az ellenállás értékének harmadik szignifikáns számjegye.
- Negyedik sáv: A szorzó.
- Ötödik sáv: A tűrés.
Például, ha egy ellenálláson a sávok sorrendje barna, fekete, fekete, barna és barna, akkor az értéke a következőképpen számítható ki:
- Barna (első sáv): 1
- Fekete (második sáv): 0
- Fekete (harmadik sáv): 0
- Barna (negyedik sáv, szorzó): $10^1 = 10$
- Barna (ötödik sáv, tűrés): ±1%
Tehát az ellenállás értéke $100 \times 10 = 1000 \Omega = 1 k\Omega$, ±1% tűréssel.
A Hat Sávos Színkód
Néhány speciális ellenálláson hat színkód található. Az első öt sáv jelentése megegyezik az öt sávos ellenálláséval, a hatodik sáv pedig általában a hőmérsékleti együtthatót jelöli (PPM/K – parts per million per Kelvin).
A Hatodik Sáv Színkódja és Jelentése
| Szín | Hőmérsékleti Együttható (PPM/K) |
|---|---|
| Fekete | – |
| Barna | ±100 |
| Vörös | ±50 |
| Narancs | ±15 |
| Sárga | ±25 |
| Zöld | – |
| Kék | ±10 |
| Ibolya | ±5 |
| Szürke | – |
| Fehér | – |
Az Ellenállások Típusai
Számos különböző típusú ellenállás létezik, amelyeket a felhasználás célja és a gyártási technológia különböztet meg.
Szénréteg Ellenállások
A szénréteg ellenállások vékony szénrétegből készülnek egy kerámia vagy üvegrúdra felvitelezve. Jellemzőjük az alacsony költség és a széleskörű elérhetőség. Általános célú alkalmazásokhoz ideálisak.
Fémréteg Ellenállások
A fémréteg ellenállások vékony fémötvözet rétegből készülnek. Pontosabbak és stabilabbak, mint a szénréteg ellenállások, ezért precízebb alkalmazásokhoz ajánlottak.
Huzaltekercselt Ellenállások
A huzaltekercselt ellenállások egy szigetelt huzal feltekercselésével készülnek egy nem vezető magra. Nagyobb teljesítmény leadására képesek, ezért tápegységekben és teljesítményelektronikai áramkörökben gyakoriak.
SMD Ellenállások (Surface Mount Devices)
Az SMD ellenállások felületszerelt alkatrészek, amelyek nagyon kicsik és közvetlenül a nyomtatott áramköri lap felületére forraszthatók. Méretüket és értéküket általában egy numerikus vagy alfanumerikus kód jelöli.
Az SMD Ellenállások Kódolása
Az SMD ellenállások értékét gyakran egy három- vagy négyjegyű kód jelzi. Az első néhány számjegy a szignifikáns számjegyeket jelöli, az utolsó számjegy pedig a szorzót (a tíz hatványát).
- Például a “103” kód egy $10 \times 10^3 = 10000 \Omega = 10 k\Omega$-os ellenállást jelent.
- A “4R7” kód egy $4.7 \Omega$-os ellenállást jelent (az ‘R’ a tizedesvessző helyett).
Potenciométerek és Trimmerek
A potenciométerek és a trimmerek olyan változtatható ellenállások, amelyek lehetővé teszik az ellenállás értékének manuális beállítását. A potenciométereket általában felhasználói interfészekben (pl. hangerőszabályozók) használják, míg a trimmereket áramkörök finomhangolására alkalmazzák.
Az Ellenállások Kapcsolása: Soros és Párhuzamos Kapcsolások
Az áramkörökben az ellenállásokat különböző módokon lehet összekapcsolni, amelyek befolyásolják az eredő ellenállást.
Soros Kapcsolás
Soros kapcsolás esetén az ellenállások egymás után vannak kötve, így az áramnak mindegyiken át kell folynia. A sorosan kapcsolt ellenállások eredő ellenállása az egyes ellenállások értékeinek összege:
$$\Large R_{eredő} = R_1 + R_2 + R_3 + \dots + R_n$$
Párhuzamos Kapcsolás
Párhuzamos kapcsolás esetén az ellenállások párhuzamosan vannak kötve, így az áram több úton folyhat. A párhuzamosan kapcsolt ellenállások eredő ellenállásának reciproka az egyes ellenállások reciprokértékeinek összege:
$$\Large \frac{1}{R_{eredő}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}$$
Két ellenállás párhuzamos kapcsolása esetén az eredő ellenállás egyszerűbben számítható:
$$\Large R_{eredő} = \frac{R_1 \times R_2}{R_1 + R_2}$$

Kombinált Kapcsolások
A valóságos áramkörökben gyakran találkozhatunk soros és párhuzamos kapcsolások kombinációival is. Az eredő ellenállás meghatározásához ilyenkor lépésről lépésre kell egyszerűsíteni az áramkört.
Az Ohm Törvénye és az Ellenállás Kapcsolata a Feszültséggel és az Árammal
Az Ohm törvénye az egyik legalapvetőbb összefüggés az elektromosságban, amely megadja a feszültség (U), az áram (I) és az ellenállás (R) közötti kapcsolatot:
$$\Large U = I \times R$$
Ebből az egyenletből kifejezhető az áram és az ellenállás is:
$$\Large I = \frac{U}{R}$$
$$\Large R = \frac{U}{I}$$
Az Ohm törvényének ismerete elengedhetetlen az áramkörök elemzéséhez és tervezéséhez. Segítségével kiszámíthatjuk az áramot egy adott feszültség és ellenállás mellett, vagy meghatározhatjuk a szükséges ellenállás értékét egy adott áram és feszültség eléréséhez.
Az Ellenállások Teljesítménye
Az ellenállások nem csak az áramot korlátozzák, hanem hőt is termelnek, amikor áram fol