A Fuzzy Logika Mélyreható Tanulmányozása: Elmélet, Alkalmazások és a Jövő Horizontja

A fuzzy logika, más néven homályos logika, egy olyan matematikai megközelítés, amely a bizonytalanság és a pontatlanság modellezésére és kezelésére szolgál. Eltér a klasszikus, Boole-féle logikától, amely csak a két igazságértéket (igaz vagy hamis) fogadja el. A fuzzy logika lehetővé teszi, hogy egy állítás részlegesen igaz vagy hamis legyen, egy 0 és 1 közötti fokozattal kifejezve az igazságtartalmat. Ez a képesség rendkívül hasznossá teszi olyan komplex rendszerek modellezésében, ahol a határvonalak nem élesek, és a nyelvi kifejezések gyakran homályosak.

A Fuzzy Logika Alapjai: A Halmazelmélet Kiterjesztése

A fuzzy logika gyökerei Lotfi A. Zadeh 1965-ös úttörő munkájához nyúlnak vissza, aki bevezette a fuzzy halmazok fogalmát. A klasszikus halmazelméletben egy elem vagy teljes mértékben tagja egy halmaznak, vagy egyáltalán nem. Ezzel szemben a fuzzy halmazelmélet lehetővé teszi, hogy egy elemnek egy tagsági foka legyen egy adott halmazhoz, amelyet egy 0 és 1 közötti értékkel fejezünk ki. Például, a “magas emberek” halmazában egy 185 cm magas ember tagsági foka magasabb lehet, mint egy 175 cm magas emberé, de mindketten valamilyen fokig tagjai lehetnek a halmaznak.

A Tagsági Függvény: A Homályosság Kvantifikálása

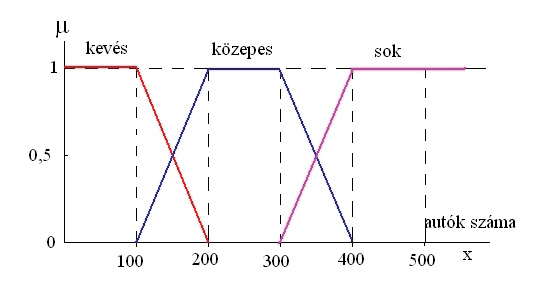
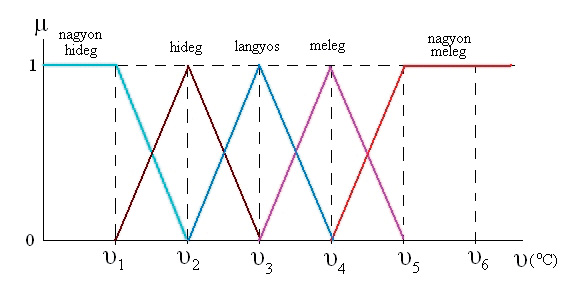
A fuzzy halmazokat a tagsági függvények írják le, amelyek minden egyes elemhez egy 0 és 1 közötti tagsági értéket rendelnek. A tagsági függvény alakja tetszőleges lehet, de a leggyakrabban használt formák közé tartoznak a háromszög, a trapéz, a Gauss-görbe és az S-görbe. A tagsági függvény megválasztása az adott probléma kontextusától és a szakértői tudástól függ. Például, a “meleg” hőmérséklet fuzzy halmazához egy olyan tagsági függvényt lehetne definiálni, amely alacsony hőmérsékleten 0-hoz közeli értéket ad, egy bizonyos tartományban növekszik 1-ig, majd magasabb hőmérsékleten ismét csökken.

Fuzzy Logikai Műveletek: A Következtetés Szabályai

A fuzzy logika kiterjeszti a klasszikus logikai műveleteket (ÉS, VAGY, NEM) a fuzzy halmazokra. A leggyakrabban használt fuzzy logikai operátorok a következők:

• Fuzzy ÉS (T-norma): Számos T-norma létezik, a leggyakoribb a minimum operátor ($\mu_{A \cap B}(x) = \min(\mu_A(x), \mu_B(x))$) és a szorzás operátor ($\mu_{A \cap B}(x) = \mu_A(x) \cdot \mu_B(x)$).

• Fuzzy VAGY (S-norma): A leggyakoribb S-norma a maximum operátor ($\mu_{A \cup B}(x) = \max(\mu_A(x), \mu_B(x))$) és az algebrai összeg operátor ($\mu_{A \cup B}(x) = \mu_A(x) + \mu_B(x) – \mu_A(x) \cdot \mu_B(x)$).
• Fuzzy NEM (Negáció): A standard negáció $\mu_{\neg A}(x) = 1 – \mu_A(x)$.

Ezek az operátorok lehetővé teszik komplex fuzzy állítások kiértékelését és a fuzzy következtetési rendszerek felépítését.

A Fuzzy Következtetési Rendszerek: Tudás Reprezentációja és Döntéshozatal

A fuzzy következtetési rendszerek (FIS), más néven fuzzy szabályalapú rendszerek, a fuzzy logika elveit alkalmazzák a tudás reprezentálására és a döntéshozatalra. Egy tipikus FIS három fő komponensből áll:

1. Fuzzifikációs egység: A bemeneti változók (amelyek általában valós számok) fuzzy halmazokká alakítása a megfelelő tagsági függvények segítségével.
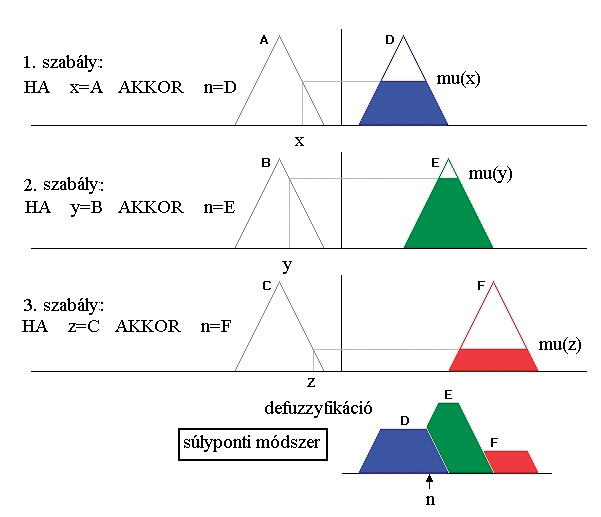
2. Szabálybázis: “HA (feltétel) AKKOR (következmény)” formátumú fuzzy szabályok gyűjteménye. A feltétel rész fuzzy állításokat tartalmaz a bemeneti változókról, a következmény rész pedig fuzzy állításokat a kimeneti változókról.
3. Következtetési mechanizmus: A szabálybázisban lévő szabályok alkalmazása a fuzzifikált bemenetekre a fuzzy kimenetek generálásához.
4. Defuzzifikációs egység: A fuzzy kimenetek visszaalakítása egyetlen, éles (crisp) kimeneti értékké, amelyet a gyakorlatban fel lehet használni. Számos defuzzifikációs módszer létezik, például a centroid (súlypont) módszer, a magasság módszer és a közép-maximum módszer.

A Mamdani és a Takagi-Sugeno-Kang Típusú FIS

Két elterjedt típusa létezik a fuzzy következtetési rendszereknek:

• Mamdani FIS: Ebben a típusban mind a szabályok feltétel, mind a következmény része fuzzy halmazokat tartalmaz. A kimenet egy fuzzy halmaz, amelyet defuzzifikálni kell a végső éles érték előállításához. A Mamdani modell intuitív és jól alkalmazható szakértői tudás alapján történő rendszerépítésre.
• Takagi-Sugeno-Kang (TSK) FIS: Ebben a típusban a szabályok következmény része nem fuzzy halmaz, hanem a bemeneti változók lineáris kombinációja (vagy egy konstans). A TSK modell gyakran simább kimeneti felületet eredményez, és matematikai szempontból könnyebben elemezhető. A végső kimenet a szabályok kimeneteinek súlyozott átlaga.

A Fuzzy Logika Széleskörű Alkalmazásai

A fuzzy logika sokféle területen bizonyította már a hatékonyságát, különösen olyan komplex rendszerek irányításában és modellezésében, ahol a hagyományos matematikai megközelítések nehézségekbe ütköznek a bizonytalanság és a pontatlanság kezelése miatt.

Irányításelmélet: Intelligens Vezérlők tervezése

A fuzzy logika sikeresen alkalmazható irányítási rendszerek tervezéséhez. A fuzzy vezérlők képesek emberi szakértői tudást beépíteni a vezérlési algoritmusokba nyelvi szabályok formájában. Például, egy fuzzy légkondicionáló rendszer a “ha a hőmérséklet magas ÉS a páratartalom magas, akkor növeld a hűtést erősen” típusú szabályokat használhat a hűtőteljesítmény beállításához. A fuzzy vezérlők robusztusak, jól alkalmazkodnak a nemlineáris rendszerekhez, és gyakran könnyebben megtervezhetők, mint a hagyományos PID vezérlők, különösen akkor, ha a rendszer modellje nehezen állítható fel pontosan.

Döntéstámogatás: Komplex döntések meghozatala bizonytalan információk alapján

A fuzzy logika értékes eszköz a döntéstámogató rendszerekben. Lehetővé teszi a bizonytalan vagy hiányos információk kezelését és a döntések meghozatalát nyelvi kifejezések és szakértői vélemények alapján. Például, egy orvosi diagnosztikai rendszer fuzzy szabályokat használhat a tünetek és a lehetséges betegségek közötti kapcsolat modellezésére, figyelembe véve a tünetek súlyosságának fokozatait.

Mintázatfelismerés: Homályos kategóriák kezelése

A mintázatfelismerés területén a fuzzy logika segíthet a homályos vagy rosszul definiált kategóriák kezelésében. Például, a képfeldolgozásban a fuzzy klaszterezési algoritmusok hatékonyan képesek a képpontokat olyan csoportokba sorolni, amelyek nem feltétlenül élesen elkülönülnek egymástól. Hasonlóképpen, a szövegbányászatban a fuzzy halmazok felhasználhatók a dokumentumok témájának vagy érzelmi töltetének homályos jellegének megragadására.

Mesterséges Intelligencia: Intelligens rendszerek építése emberi gondolkodásmóddal

A fuzzy logika fontos építőköve lehet az mesterséges intelligencia (MI) rendszereinek. Lehetővé teszi, hogy az MI rendszerek jobban megértsék és kezeljék az emberi nyelvet, a bizonytalanságot és a nem egyértelmű helyzeteket. A fuzzy logika integrálható más MI technikákkal, például neurális hálózatokkal és genetikus algoritmusokkal, hibrid intelligens rendszerek létrehozásához, amelyek ötvözik az egyes módszerek erősségeit.

A Fuzzy Logika Előnyei és Hátrányai

Előnyök

• A bizonytalanság és a pontatlanság kezelése: Képes modellezni a valós világ komplexitását, ahol a határok gyakran nem élesek.
• Nyelvi leírás: Lehetővé teszi a szakértői tudás intuitív, nyelvi szabályok formájában történő reprezentációját.
• Robusztusság: A fuzzy rendszerek gyakran robusztusabbak a zajjal és a modellbeli pontatlanságokkal szemben, mint a hagyományos módszerek.
• Könnyű tervezés: Bizonyos esetekben a fuzzy vezérlők tervezése egyszerűbb lehet, mint a hagyományos analitikus módszerekkel.

Hátrányok

• A tagsági függvények és a szabályok meghatározása: Ezek megtervezése szubjektív lehet, és szakértői tudást igényel.
• Nincs szisztematikus tervezési módszertan: A fuzzy rendszerek tervezése gyakran kísérletezésen és heurisztikákon alapul.
• Számítási komplexitás: Egyes fuzzy következtetési módszerek számításigényesek lehetnek, különösen komplex rendszerek esetén.
• Nehéz analitikus elemzés: A fuzzy rendszerek viselkedésének formális matematikai elemzése bonyolult lehet.

A Fuzzy Logika Jövőbeli Irányai és Potenciálja

A fuzzy logika továbbra is aktív kutatási terület, és számos izgalmas jövőbeli potenciált rejt magában.

Hibrid Intelligens Rendszerek: A fuzzy logika integrálása más MI technikákkal

A jövőben várhatóan egyre több hibrid intelligens rendszer fog létrejönni, amelyek ötvözik a fuzzy logika előnyeit más MI módszerekkel, például a neurális hálózatokkal (neuro-fuzzy rendszerek) és a genetikus algoritmusokkal (fuzzy genetikus rendszerek). Ezek a hibrid megközelítések kihasználhatják az egyes technikák erősségeit a komplex problémák hatékonyabb megoldása érdekében.

Big Data és Fuzzy Logika: A nagyméretű, bizonytalan adathalmazok kezelése

A big data korszakában a fuzzy logika ígéretes megközelítést kínál a nagyméretű, gyakran bizonytalan és pontatlan adathalmazok elemzésére és modellezésére. A fuzzy módszerek segíthetnek a zajos adatokból való hasznos információ kinyerésében és a homályos mintázatok azonosításában.

Ember-Gép Interakció: Természetesebb és intuitívabb interfészek

A fuzzy logika hozzájárulhat a természetesebb és intuitívabb ember-gép interakciók fejlesztéséhez. A fuzzy alapú rendszerek jobban képesek megérteni az emberi nyelv homályosságát és a felhasználói preferenciák árnyalatait, ami javíthatja a felhasználói élményt.

Okos Rendszerek és IoT: Intelligens döntéshozatal a hálózatba kötött eszközökben

Az Internet of Things (IoT) terjedésével a fuzzy logika szerepet játszhat az okos rendszerek fejlesztésében. A hálózatba kötött eszközök által generált adatok alapján a fuzzy logika lehetővé teheti az intelligens, helyi döntéshozatalt, figyelembe véve a környezeti bizonytalanságokat és a felhasználói igényeket.

Összegzés: A Fuzzy Logika Jelentősége a 21. Században

A fuzzy logika egy erőteljes és rugalmas eszköz a bizonytalanság és a pontatlanság kezelésére a komplex rendszerek modellezésében és irányításában. Széleskörű alkalmazásai a mérnöki tudományoktól a mesterséges intelligenciáig mutatják sokoldalúságát és relevanciáját. Ahogy a világ egyre összetettebbé válik, a fuzzy logika képessége a valós világ homályosságának megragadására egyre értékesebbé válik a technológiai fejlődés szempontjából.

Reméljük, hogy ez a részletes áttekintés segített megérteni a fuzzy logika alapelveit, alkalmazásait és jövőbeli potenciálját. Ha további kérdései vannak, ne habozzon felvenni velünk a kapcsolatot!