A Helyzeti Energia Fogalma: Mélyreható Értelmezés és Alkalmazások

Mi a Helyzeti Energia? A Potenciális Energia Alapjai

A helyzeti energia, más néven potenciális energia, egy olyan tárolt energiaforma, amely egy objektum helyzetéből, konfigurációjából vagy állapotából ered. Ez az energia akkor képes munkát végezni, amikor az objektum felszabadul, és helyzete vagy konfigurációja megváltozik. A helyzeti energia nem önmagában létezik, hanem mindig egy erőtérrel (például gravitációs, elektromos vagy rugalmas) kölcsönhatásban lévő objektumhoz kapcsolódik. Amikor egy objektum egy ilyen erőtérben mozog, a mező munkát végezhet rajta, megváltoztatva a helyzeti energiáját, vagy az objektum végezhet munkát a mező ellen, szintén megváltoztatva a helyzeti energiáját.

A potenciális energia fogalma kulcsfontosságú a fizika számos területén, a klasszikus mechanikától az elektromágnességen át a modern fizikáig. Segítségével leírhatjuk a rendszerek stabilitását, az energiaátalakulásokat és a mozgás törvényeit. A mindennapi életben is gyakran találkozunk a helyzeti energiával, például amikor egy hegy tetején álló kőnek potenciális energiája van a gravitációs mezőben, vagy amikor egy megfeszített rugóban rugalmas helyzeti energia tárolódik.

A Gravitációs Helyzeti Energia: Magyarázat és Képlet

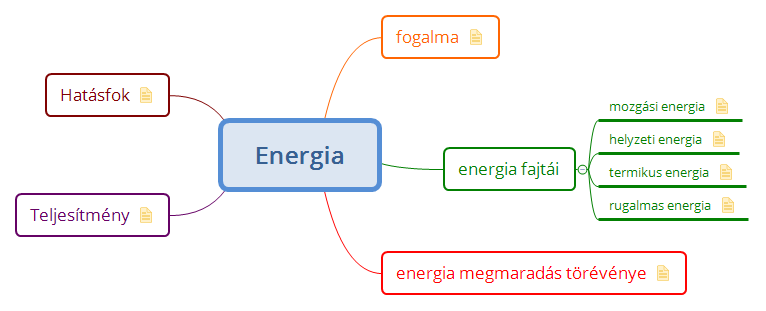
A gravitációs helyzeti energia egy objektum tömegéből és a gravitációs mezőben elfoglalt helyzetéből származó potenciális energia. A Föld felszínének közelében a gravitációs mező közelítőleg homogénnek tekinthető, és a gravitációs helyzeti energia a következő képlettel számítható ki:

\\displaystyle E\_p \= mgh

ahol:

• \\displaystyle E\_p a gravitációs helyzeti energia (joule-ban mérve, J)
• \\displaystyle m az objektum tömege (kilogrammban mérve, kg)
• \\displaystyle g a gravitációs gyorsulás (a Földön körülbelül \\displaystyle 9\.81 \\, m/s^2)
• \\displaystyle h az objektum magassága egy referencia-szinthez képest (méterben mérve, m)

Fontos megjegyezni, hogy a referencia-szint megválasztása önkényes, de a helyzeti energia *változása* független ettől a választástól. Például, ha egy objektumot egy bizonyos magasságról leejtünk, a gravitációs helyzeti energiájának csökkenése mindig ugyanakkora lesz, függetlenül attól, hogy a referencia-szintet a földfelszínen vagy egy annál alacsonyabb ponton vesszük fel.

Példák a Gravitációs Helyzeti Energiára

• Egy polcon álló könyvnek gravitációs helyzeti energiája van a földhöz képest. Minél magasabban van a polc, annál nagyobb ez az energia. Amikor a könyv leesik, ez a helyzeti energia mozgási energiává alakul.
• Egy víztározóban felgyülemlett víznek jelentős gravitációs helyzeti energiája van a völgyben lévő turbinákhoz képest. Amikor a vizet leengedik, ez az energia a turbinákat meghajtva elektromos energiává alakul.
• Egy hegycsúcson lévő síelőnek nagy a gravitációs helyzeti energiája a völgy aljához képest. Leereszkedés közben ez az energia részben mozgási energiává, részben pedig hővé alakul a súrlódás miatt.

A Rugalmas Helyzeti Energia: A Megfeszített Rugók Energiája

A rugalmas helyzeti energia egy rugalmasan deformált objektumban (például egy megfeszített vagy összenyomott rugóban) tárolt potenciális energia. Ez az energia akkor keletkezik, amikor egy külső erő munkát végez a rugón, megváltoztatva annak alakját. A rugalmas helyzeti energia a rugó eredeti alakjába való visszatérésre való törekvéséből származik.

Egy ideális rugó által tárolt rugalmas helyzeti energia a Hooke-törvény alapján számítható ki:

\\displaystyle E\_p \= \\frac\{1\}\{2\}kx^2

ahol:

• \\displaystyle E\_p a rugalmas helyzeti energia (joule-ban, J)
• \\displaystyle k a rugóállandó (newton per méterben mérve, N/m), amely a rugó merevségét jellemzi
• \\displaystyle x a rugó egyensúlyi helyzetétől való elmozdulás (méterben, m)

A képletből látható, hogy a rugalmas helyzeti energia arányos az elmozdulás négyzetével. Ez azt jelenti, hogy a rugó megnyújtásának vagy összenyomásának kétszerese négyszeresére növeli a tárolt energiát.

Példák a Rugalmas Helyzeti Energiára

• Egy megfeszített íjban rugalmas helyzeti energia tárolódik. Amikor az íjhúr elengedik, ez az energia a nyílnak mozgási energiává alakul.
• Egy összenyomott rugóban, például egy autó felfüggesztésében, rugalmas helyzeti energia van. Amikor a rugó kinyílik, ez az energia hatással van az autó mozgására.
• Egy gumiszalag megnyújtásakor rugalmas helyzeti energiát tárolunk benne. Amikor elengedjük, ez az energia más objektumok (például egy papírgolyó) mozgatására használható fel.

Az Elektromos Helyzeti Energia: Töltött Részecskék Kölcsönhatása

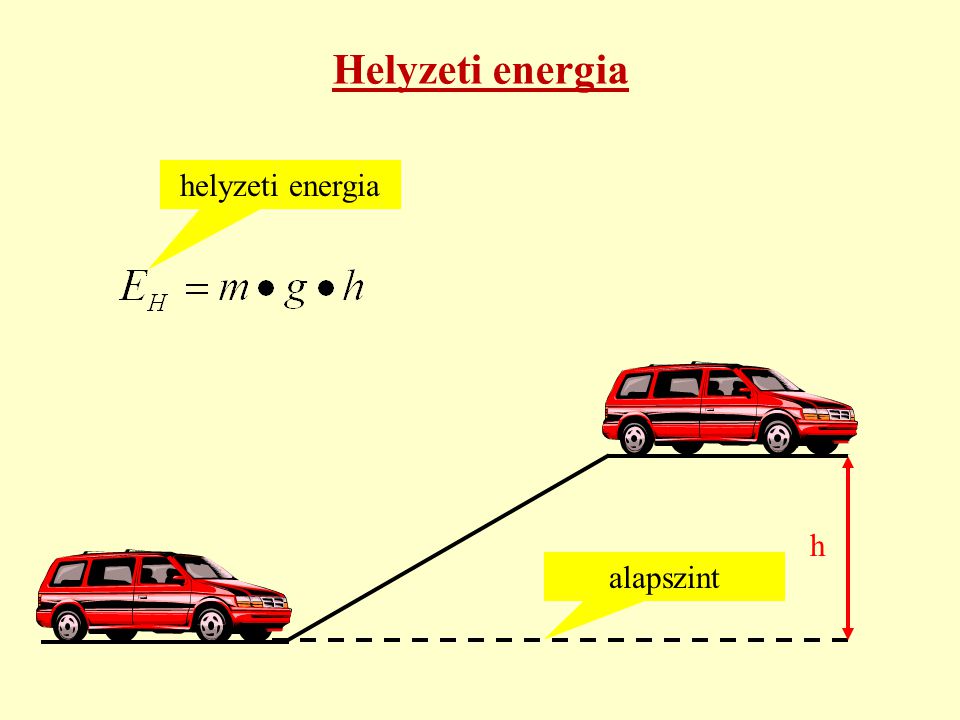
Az elektromos helyzeti energia két vagy több elektromosan töltött részecske relatív helyzetéből származó potenciális energia. Ez az energia az elektromos mező által a töltött részecskékre kifejtett erővel kapcsolatos. Két ponttöltés közötti elektromos helyzeti energia a Coulomb-törvényből vezethető le:

\\displaystyle U \= k \\frac\{q\_1 q\_2\}\{r\}

ahol:

• \\displaystyle U az elektromos helyzeti energia (joule-ban, J)
• \\displaystyle k a Coulomb-állandó (\\displaystyle \\approx 8\.9875 \\times 10^9 \\, N \\cdot m^2/C^2)
• \\displaystyle q\_1 és \\displaystyle q\_2 a két ponttöltés nagysága (coulomb-ban, C)
• \\displaystyle r a két töltés közötti távolság (méterben, m)

Az elektromos helyzeti energia pozitív, ha a két töltés azonos előjelű (mindkettő pozitív vagy mindkettő negatív), és negatív, ha ellentétes előjelűek. A nulla helyzeti energia konvenciója általában az, hogy a töltések végtelen távolságban vannak egymástól.

Példák az Elektromos Helyzeti Energiára

• Egy atommag és egy elektron közötti elektromos helyzeti energia felelős az atom stabilitásáért. Az elektron alacsonyabb potenciális energiájú pályákra törekszik.
• Két azonos előjelű töltés közeledése növeli az elektromos helyzeti energiát, mivel munkát kell végezni az elektromos taszítóerő ellen.
• Két ellentétes előjelű töltés közeledése csökkenti az elektromos helyzeti energiát, mivel az elektromos vonzóerő munkát végez a töltéseken.

A Kémiai Helyzeti Energia: Az Atomok Kötéseiben Tárolt Energia

A kémiai helyzeti energia az atomok és molekulák kötéseiben tárolt potenciális energia. Ez az energia az elektronok és az atommagok közötti elektromágneses kölcsönhatásokból származik. Kémiai reakciók során ezek a kötések felbomolhatnak és újak jöhetnek létre, ami energia felszabadulásával vagy elnyelésével járhat.

A kémiai helyzeti energia nem olyan egyszerűen számítható ki, mint a gravitációs vagy a rugalmas helyzeti energia, mivel az atomok és molekulák komplex elektronstruktúrájától függ. Azonban a kémiai reakciók során felszabaduló vagy elnyelt hőmennyiség (entalpiaváltozás) közvetlenül kapcsolódik a kémiai kötésekben bekövetkező energiaváltozásokhoz.

Példák a Kémiai Helyzeti Energiára

• A fa vagy a fosszilis tüzelőanyagok kémiai helyzeti energiát tartalmaznak. Égés során ez az energia hővé és fényé alakul.
• Az élelmiszerekben tárolt kémiai energia a szervezetünk számára biztosítja a működéshez szükséges energiát. A metabolizmus során a komplex molekulák lebomlanak, és energia szabadul fel.
• Az akkumulátorokban tárolt kémiai energia elektromos energiává alakítható kémiai reakciók révén.

A Magasságtól Függő Helyzeti Energia Részletesebben

A magasságtól függő helyzeti energia, ahogy korábban említettük, a gravitációs helyzeti energia speciális esete a Föld felszínének közelében. A \\displaystyle E\_p \= mgh képlet jól közelíti ezt az energiát, feltéve, hogy a magasságváltozás nem túl nagy, és a gravitációs gyorsulás (\\displaystyle g) konstansnak tekinthető.

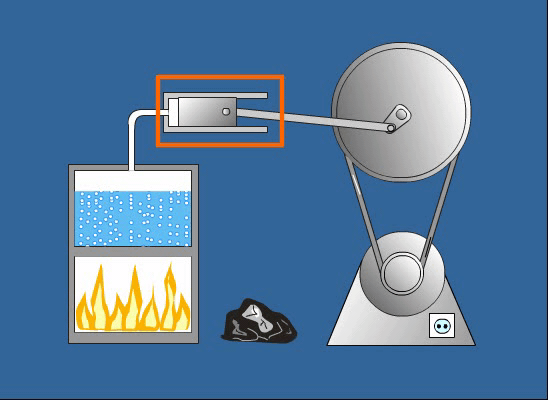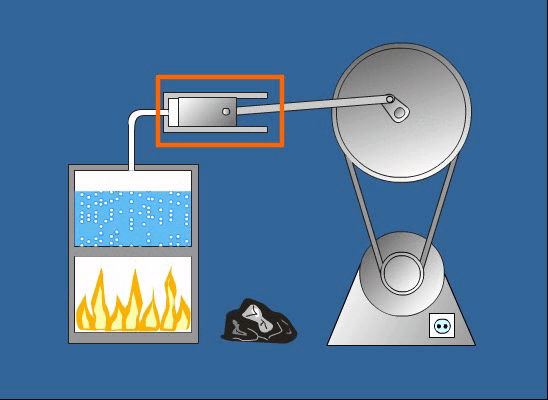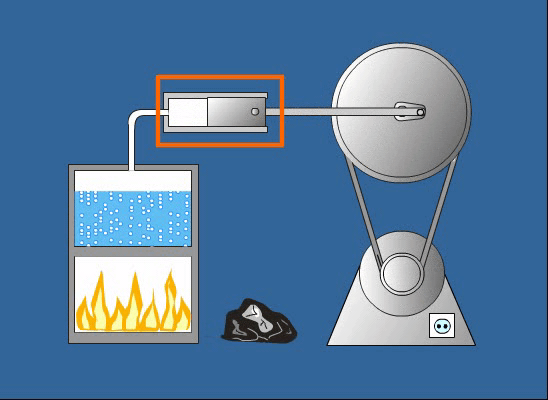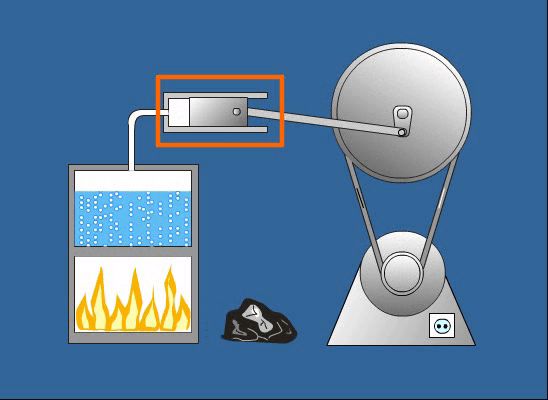
Ha azonban nagy magasságváltozásokról van szó, vagy ha távolabb kerülünk a Földtől, a gravitációs erő már nem tekinthető konstansnak, és a helyzeti energia képlete is megváltozik. Általánosabban, a két tömeg közötti gravitációs potenciális energia a következőképpen írható le:

\\displaystyle U \= \-G \\frac\{m\_1 m\_2\}\{r\}

ahol:

• \\displaystyle U a gravitációs potenciális energia
• \\displaystyle G a gravitációs állandó (\\displaystyle \\approx 6\.674 \\times 10^\{\-11\} \\, N \\cdot m^2/kg^2)
• \\displaystyle m\_1 és \\displaystyle m\_2 a két tömeg
• \\displaystyle r a két tömeg középpontja közötti távolság

Ebben az esetben a nulla potenciális energia konvenciója az, hogy a két tömeg végtelen távolságban van egymástól. A negatív előjel azt jelzi, hogy a gravitációs erő vonzó, és munkát kell végezni a tömegek szétválasztásához.

Alkalmazások a Csillagászatban

A gravitációs helyzeti energia kulcsszerepet játszik a csillagászatban. Például:

• A bolygók Nap körüli mozgását a Nap gravitációs helyzeti energiája és a bolygók mozgási energiája határozza meg.
• A csillagok kialakulása során a gázfelhők gravitációs összehúzódása helyzeti energia felszabadulásával jár, ami a csillag felmelegedéséhez vezet.
• A fekete lyukak rendkívül erős gravitációs terében a helyzeti energia fogalma relativisztikus korrekciókat igényel.

A Rugóállandó és a Rugalmas Helyzeti Energia Kapcsolata Mélyebben

A rugóállandó (\\displaystyle k) egy mérőszám, amely megmutatja, hogy egy rugó mennyire ellenáll a deformációnak. Nagyobb rugóállandó azt jelenti, hogy nagyobb erőre van szükség a rugó adott mértékű megnyújtásához vagy összenyomásához. A rugóállandó a rugó anyagától, méretétől és alakjától függ.

A rugalmas helyzeti energia (\\displaystyle E\_p \= \\frac\{1\}\{2\}kx^2) közvetlenül arányos a rugóállandóval. Ez azt jelenti, hogy egy merevebb rugó (nagyobb \\displaystyle k) ugyanakkora elmozdulás esetén több rugalmas helyzeti energiát tárol, mint egy lágyabb rugó (kisebb \\displaystyle k).

Energiatárolás Rugókkal

A rugók hatékonyan képesek energiát tárolni rugalmas helyzeti energia formájában. Ezt az elvet számos technológiai alkalmazásban kihasználják:

• A mechanikus órákban egy felhúzott rugó tárolja az energiát, amely a fogaskerekeken keresztül a mutatók mozgatására szolgál.
• A rugós mérlegek a rugó megnyúlásának mértékéből következtetnek a rájuk ható erőre (és így a mérendő tárgy tömegére).
• A járművek felfüggesztésében használt rugók elnyelik az útegyenetlenségekből származ