A Mágneses Fluxus Részletes Tanulmánya

Ebben az átfogó cikkben részletesen feltárjuk a mágneses fluxus fogalmát, jelentőségét a fizika és a mérnöki tudományok területén. Megvizsgáljuk annak alapvető definíciójától kezdve a gyakorlati alkalmazásáig terjedő széles spektrumát. Célunk, hogy egy olyan mélyreható és érthető magyarázatot nyújtsunk, amely mind a diákok, mind a szakemberek számára értékes forrásként szolgál.

A Mágneses Fluxus Alapjai

Mi a Mágneses Fluxus?

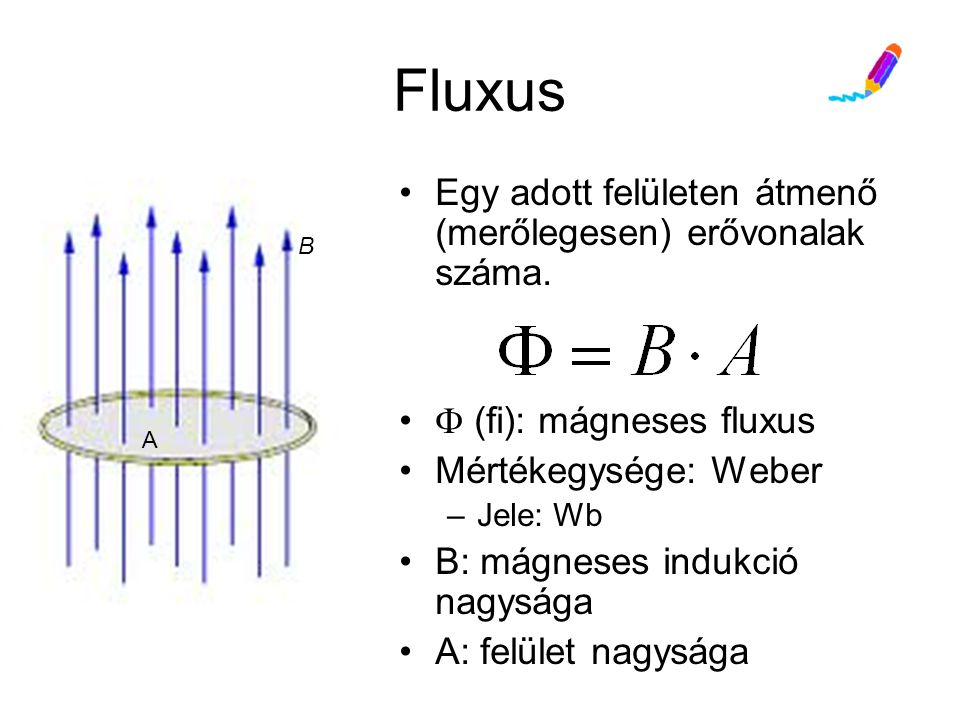
A mágneses fluxus (\\Phi\_B) egy adott felületen áthaladó mágneses tér mennyiségének a mérőszáma. Képzeljünk el egy mágneses teret, amelyet vonalak szemléltetnek. A mágneses fluxus arányos azzal a vonalszámmal, amely egy adott felületet áthalad. Pontosabban, a mágneses fluxus a mágneses indukcióvektor (\\mathbf\{B\}) és a felület normálvektorának (\\mathbf\{A\}) skaláris szorzata, integrálva a felületen.

A Mágneses Fluxus Képlete

Matematikailag a mágneses fluxust a következőképpen fejezhetjük ki:

\\Phi\_B \= \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}

ahol:

• \\Phi\_B a mágneses fluxus (Weberben, Wb)
• \\mathbf\{B\} a mágneses indukcióvektor (Tesla, T)
• d\\mathbf\{A\} a felület egy infiniteszimális elemének vektoros területe, amelynek iránya a felületre merőleges

Egyenletes mágneses tér és sík felület esetén, ahol a mágneses tér a felület normáljával \\theta szöget zár be, a fluxus egyszerűbben számítható:

\\Phi\_B \= BA \\cos \\theta

ahol:

• B a mágneses tér erőssége
• A a felület területe

• \\theta a mágneses tér és a felület normáljának szöge

A Mágneses Fluxus Mértékegysége

A mágneses fluxus SI mértékegysége a weber (Wb). Egy weber egyenlő egy tesla szorozva egy négyzetméterrel (1 Wb = 1 T⋅m²). A korábbi CGS rendszerben a mágneses fluxus mértékegysége a maxwell (Mx) volt. Az átváltás a két egység között a következő: 1 Wb = 10^8 Mx.

A Mágneses Fluxus Fizikai Jelentősége

Faraday Indukciós Törvénye

A mágneses fluxus központi szerepet játszik az elektromágneses indukció jelenségének leírásában, amelyet Faraday indukciós törvénye fogalmaz meg. Ez a törvény kimondja, hogy egy zárt vezetőben indukált elektromotoros erő (EMF) egyenlő a vezetőt körülvevő mágneses fluxus időbeli változásának negatívjával:

\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}

Ez az alapvető törvény magyarázza meg az elektromos generátorok, transzformátorok és sok más elektromágneses eszköz működését.

Gauss Törvénye a Mágnesességre

A mágneses fluxus egy másik fontos összefüggése a Gauss törvénye a mágnesességre, amely a Maxwell-egyenletek egyike. Ez a törvény kimondja, hogy egy zárt felületen átmenő mágneses fluxus mindig nulla:

\\oint \\mathbf\{B\} \\cdot d\\mathbf\{A\} \= 0

Ez azt jelenti, hogy nincsenek mágneses monopólusok; a mágneses térvonalak mindig zárt hurkokat alkotnak.

A Mágneses Fluxus Mérése

Fluxusmérők

A mágneses fluxus közvetlen mérése speciális eszközökkel, úgynevezett fluxusmérőkkel történhet. Ezek az eszközök általában egy mérőtekercset és egy integrátort tartalmaznak. Amikor a mágneses fluxus megváltozik a mérőtekercsen keresztül, egy elektromotoros erő indukálódik, amelynek nagysága arányos a fluxus változásának sebességével. Az integrátor ezután kiszámítja a teljes fluxusváltozást.

Hall-effektus Szenzorok

A Hall-effektus szenzorok szintén használhatók a mágneses tér mérésére, amelyből aztán a fluxus is meghatározható, ha ismerjük a felületet, amelyen a tér áthalad. Ezek a szenzorok azon az elven működnek, hogy egy árammal átfolyatott vezetőben, amelyet egy mágneses térbe helyeznek, a töltött részecskékre a Lorentz-erő hat, ami feszültségkülönbséget hoz létre a vezető oldalain.

A Mágneses Fluxus Alkalmazásai

Elektromos Generátorok

Az elektromos generátorok a mágneses fluxus változásán alapulnak a villamos energia előállításához. Egy tekercset forgatnak egy mágneses térben, vagy egy mágneses teret mozgatnak egy tekercs körül, ami a tekercsen keresztülmenő mágneses fluxus időbeli változását eredményezi. Ez a változás elektromotoros erőt indukál a tekercsben, létrehozva ezzel elektromos áramot.

Transzformátorok

A transzformátorok két vagy több tekercsből állnak, amelyek egy közös mágneses magon helyezkednek el. Az egyik tekercsben (primer tekercs) folyó váltakozó áram változó mágneses fluxust hoz létre a magban. Ez a változó fluxus indukál egy elektromotoros erőt a másik tekercsben (szekunder tekercs), lehetővé téve a feszültség átalakítását.

Induktív Érzékelők

Számos induktív érzékelő működik a mágneses fluxus változásának elvén. Például a fémérzékelők változást észlelnek a mágneses fluxusban, amelyet egy fémtárgy közelsége okoz. Hasonló elven működnek az induktív közelségkapcsolók is.

Mágneses Adatrögzítés

A mágneses adatrögzítés, amelyet merevlemezeken és mágnescsíkos kártyákon használnak, szintén a mágneses fluxus elvén alapul. Az adatok a mágneses anyag kis területeinek mágnesezési irányának megváltoztatásával kerülnek rögzítésre. Az olvasófej érzékeli ezeknek a területeknek a mágneses fluxusát, és visszaalakítja azokat elektromos jelekké.

Összefoglalás

A mágneses fluxus egy alapvető fogalom az elektromágnesség területén, amely leírja a mágneses tér egy adott felületen való áthaladását. Számos fontos fizikai törvény és technológiai alkalmazás alapját képezi, beleértve az elektromágneses indukciót, az elektromos generátorokat, a transzformátorokat és a mágneses adatrögzítést. A mágneses fluxus megértése elengedhetetlen az elektromágneses jelenségek és az azokon alapuló technológiák mélyebb megértéséhez.

A Mágneses Fluxus Részletesebb Matematikai Megközelítése

A Felületi Integrál Jelentősége

A mágneses fluxus definíciójában szereplő felületi integrál (\\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}) kulcsfontosságú a fogalom pontos megértéséhez. Ez az integrál azt fejezi ki, hogy a mágneses fluxus a mágneses indukcióvektor és a felület infiniteszimális területeinek skaláris szorzatának összege a teljes felületen. A skaláris szorzat \(\\mathbf\{B\} \\cdot d\\mathbf\{A\} \= B dA \\cos \\theta\) figyelembe veszi a mágneses tér irányának és a felület orientációjának egymáshoz viszonyított helyzetét.

Nem Egyenletes Mágneses Tér Esetén

Ha a mágneses tér nem egyenletes a felületen, vagy ha a felület nem sík, akkor a fluxus kiszámításához a felületi integrált kell alkalmaznunk. Ekkor a felületet apró, dA területű elemekre bontjuk, minden egyes elemre kiszámítjuk a \\mathbf\{B\} \\cdot d\\mathbf\{A\} szorzatot, majd ezeket összegezzük (integráljuk) a teljes felületre.

Példa a Fluxus Számítására

Tekintsünk egy példát: egy A területű sík felületet egy egyenletes \\mathbf\{B\} mágneses térbe helyezünk. Ha a mágneses tér a felület normáljával \\theta szöget zár be, akkor a mágneses fluxus \\Phi\_B \= BA \\cos \\theta. Ha a mágneses tér párhuzamos a felület normáljával (\\theta \= 0^\\circ), akkor \\cos \\theta \= 1, és a fluxus maximális: \\Phi\_B \= BA. Ha a mágneses tér párhuzamos a felülettel (\\theta \= 90^\\circ), akkor \\cos \\theta \= 0, és a fluxus nulla.

A Mágneses Fluxus Változásának Következményei

Lenz Törvénye

Faraday indukciós törvényével szorosan összefügg a Lenz törvénye, amely megadja az indukált áram irányát. Lenz törvénye kimondja, hogy az indukált áram olyan irányú, hogy mágneses tere ellentétes a fluxusváltozást okozó mágneses tér változásával. Ez a negatív előjel Faraday törvényében (\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}) ennek a törvénynek a következménye.

Elektromágneses Erőterek

A változó mágneses fluxus elektromos erőteret hoz létre. Ez az összefüggés a Maxwell-egyenletek egyikében, a Faraday-féle indukciós törvény általánosított formájában jelenik meg:

\\oint \\mathbf\{E\} \\cdot d\\mathbf\{l\} \= \-\\frac\{d\}\{dt\} \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}

Ez az egyenlet azt mutatja, hogy egy zárt görbe mentén vett elektromos tér vonalintegrálja (az indukált elektromotoros erő) egyenlő a görbe által határolt felületen áthaladó mágneses fluxus időbeli változásának negatívjával.

További Alkalmazások és Koncepciók

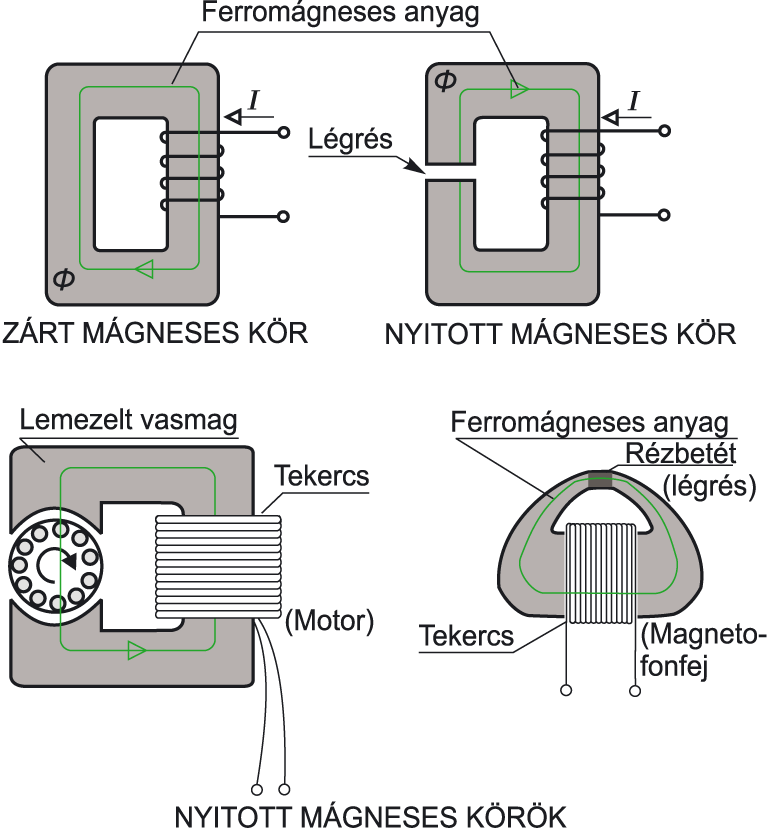
Mágneses Áramkörök

A mágneses fluxus fogalma a mágneses áramkörök analízisében is fontos szerepet játszik. A mágneses áramkörökben a mágneses fluxus analóg az elektromos árammal, a magnetomotoros erő (MMF) az elektromos feszültséggel, és a reluktancia az elektromos ellenállással. Ez az analógia segít a mágneses rendszerek, például elektromágnesek és transzformátorok tervezésében és elemzésében.

A Mágneses Fluxus Kvantálása

Bizonyos fizikai rendszerekben, például szupravezetőkben, a mágneses fluxus kvantált. Ez azt jelenti, hogy a fluxus csak bizonyos diszkrét értékeket vehet fel, amelyek a fluxuskvantum (\\Phi\_0 \= h / \(2e\) \\approx 2\.0678 \\times 10^\{\-15\} \\, \\text\{Wb\}) egész számú többszörösei. Ez a jelenség a szupravezetés kvantummechanikai természetének egyik megnyilvánulása.

A Mágneses Fluxus Szerepe a Kozmológiában

A mágneses fluxus a kozmológiában is felbukkan, például a csillagok és galaxisok mágneses terének kialakulásában és fenntartásában. A magnetohidrodinamika (MHD) a plazmák és más elektromosan vezető közegek mozgását és mágneses terét tanulmányozza, ahol a mágneses fluxus megőrzése fontos szerepet játszik.

Összegzés és Jövőbeli Kilátások

A mágneses fluxus továbbra is a fizika és a technológia egyik alapvető fogalma marad. Az elektromágneses jelenségek megértésének kulcsa, és számos modern technológia működésének alapját képezi. A kutatások folyamatosan új alkalmazásokat tárnak fel, például az anyagtudományban, az orvosi képalkotásban (MRI), és a kvantumtechnológiák területén. A mágneses fluxus pontos mérése és manipulálása a jövő technológiai fejlesztéseinek fontos területe lesz.

A Mágneses Fluxus és a Maxwell-egyenletek

A Maxwell-egyenletek Áttekintése

A Maxwell-egyenletek az elektromágnesség alapvető törvényeit foglalják össze. Négy egyenletből állnak, amelyek leírják, hogyan keletkezik és hogyan viselkedik az elektromos és mágneses tér, valamint azok kölcsönhatásait az elektromos töltésekkel és áramokkal. A mágneses fluxus fogalma több Maxwell-egyenletben is központi szerepet játszik.

Gauss Törvénye az Elektromossághoz

Bár nem közvetlenül a mágneses fluxussal kapcsolatos, érdemes megemlíteni a Gauss törvényét az elektromossághoz, amely kimondja, hogy egy zárt felületen átmenő elektromos fluxus arányos a felület által bezárt elektromos töltéssel:

\\oint \\mathbf\{E\} \\cdot d\\mathbf\{A\} \= \\frac\{Q\_\{enc\}\}\{\\epsilon\_0\}

Ez az egyenlet analóg a mágnesességre vonatkozó Gauss törvénnyel, de itt a forrás az elektromos töltés, míg a mágnesesség esetében nincsenek ismert mágneses monopólusok.

Faraday Indukciós Tör