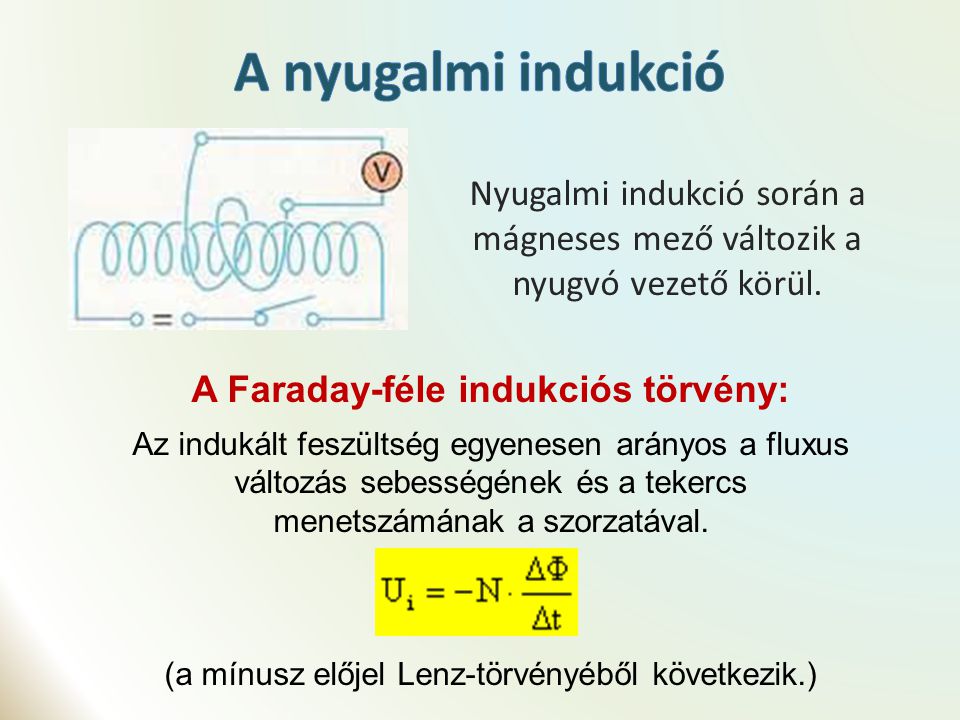
Magneses Indukcio Fogalma
A mágneses indukció fogalma és részletes magyarázata
Ebben a kimerítő cikkben mélyrehatóan feltárjuk a mágneses indukció lenyűgöző jelenségét. Célunk, hogy egy átfogó képet nyújtsunk erről az alapvető fizikai fogalomról, amely az elektromágnesesség megértésének sarokköve. Részletesen elemezzük a definícióját, a hozzá kapcsolódó alapelveket, a matematikai leírását, a mérési egységeit, valamint a gyakorlati alkalmazásait a mindennapi életben és a modern technológiában. Kísérletekkel és szemléletes példákkal illusztráljuk a jelenséget, hogy az olvasó számára a lehető legvilágosabb és legérthetőbb legyen.
Mi a mágneses indukció? A definíció részletes elemzése
A mágneses indukció, más néven mágneses fluxussűrűség vagy röviden B-mező, egy vektormennyiség, amely leírja a mágneses tér erősségét és irányát egy adott pontban. Képzeljünk el egy olyan teret, ahol mágneses hatások érvényesülnek. A mágneses indukció megmutatja, hogy egy mozgó töltésre vagy egy árammal átjárt vezetőre mekkora erő hat ezen a ponton, és milyen irányban. Ez a fogalom elengedhetetlen az elektromágneses jelenségek, mint például az elektromos motorok, generátorok és transzformátorok működésének megértéséhez.
A mágneses indukció mint vektormennyiség
Fontos hangsúlyozni, hogy a mágneses indukció egy vektormennyiség, ami azt jelenti, hogy nemcsak nagysága van, hanem iránya is. Az irányát hagyományosan úgy definiáljuk, hogy az a方向ba mutat, amerre egy képzeletbeli északi pólusú tesztmágnes elmozdulna a tér adott pontjában. A nagysága pedig azt adja meg, hogy milyen erős a mágneses hatás. Ezt a kettős tulajdonságot vektorokkal ábrázoljuk, ahol a vektor hossza a nagyságot, a nyíl pedig az irányt jelöli.
A mágneses indukció és a mágneses tér közötti kapcsolat
A mágneses tér egy olyan térrész, ahol mágneses erők hatnak. A mágneses indukció ennek a térnek egy lokális jellemzője. Minden pontban a mágneses térben definiálhatunk egy mágneses indukció vektort. Különböző források hozhatnak létre mágneses teret, például állandó mágnesek vagy elektromos árammal átjárt vezetők. Az általuk létrehozott mágneses tér minden pontjában létezik egy jól definiált mágneses indukció.
A mágneses indukció matematikai leírása és képletei
A mágneses indukciót pontosan leírhatjuk matematikai egyenletek segítségével. Ezek az egyenletek nemcsak a jelenség kvantitatív megértéséhez elengedhetetlenek, hanem lehetővé teszik a mágneses mezőkkel kapcsolatos számításokat és előrejelzéseket is.
A Lorentz-erő és a mágneses indukció kapcsolata
A mágneses indukció egyik legfontosabb definíciója a Lorentz-erőn keresztül történik. Egy q töltésű részecskére, amely \\mathbf\{v\} sebességgel mozog egy \\mathbf\{B\} mágneses indukciójú térben, a mágneses erő (\\mathbf\{F\}\_m) a következőképpen adható meg:
\\mathbf\{F\}\_m \= q \(\\mathbf\{v\} \\times \\mathbf\{B\}\)
Ez az egyenlet megmutatja, hogy a mágneses erő merőleges mind a részecske sebességére, mind a mágneses indukció vektorára. A kereszttermék (\\times) eredményezi a erő irányát, amelyet a jobbkéz-szabállyal határozhatunk meg. Ha a töltés pozitív, akkor a mágneses erő iránya a jobb kezünk hüvelykujjának irányába mutat, ha az ujjaink a sebesség irányába görbülnek, és a tenyerünk a mágneses indukció irányába néz.
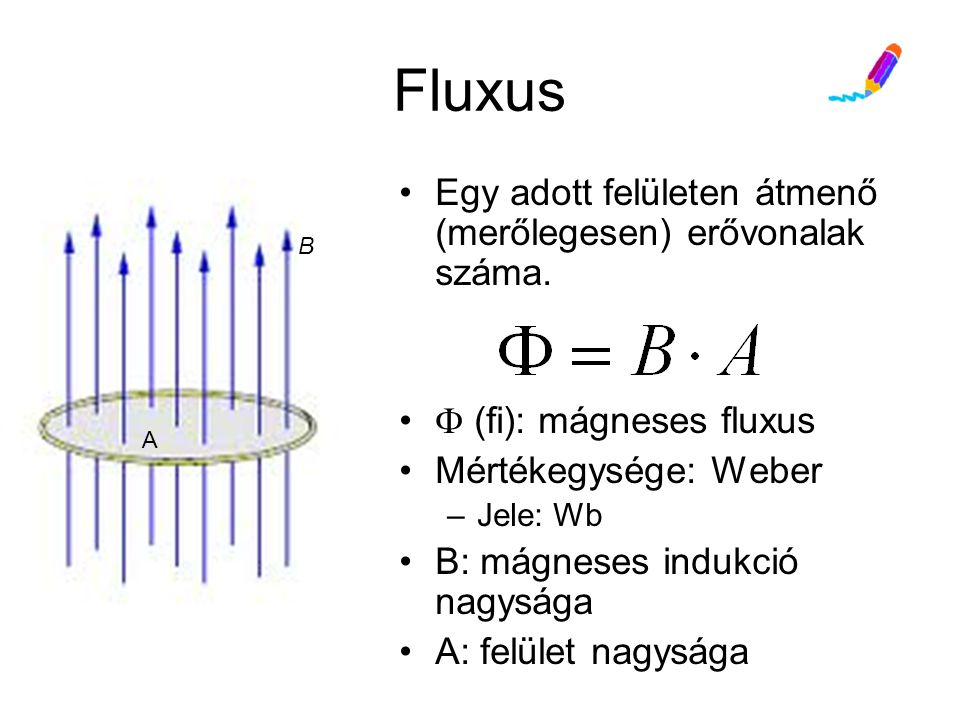
A mágneses fluxus és a mágneses indukció kapcsolata
Egy másik fontos fogalom a mágneses fluxus (\\Phi\_B), amely megadja, hogy mennyi a mágneses mező “áramlik át” egy adott felületen. A mágneses fluxus a mágneses indukció és a felület vektoros szorzatának integrálja:
\\Phi\_B \= \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}
Ha a mágneses mező homogén a felületen, és a felület normálvektora párhuzamos a mágneses indukcióval, akkor az egyenlet egyszerűsödik:
\\Phi\_B \= B A \\cos \\theta
ahol B a mágneses indukció nagysága, A a felület területe, és \\theta a mágneses indukció és a felület normálvektora közötti szög.
A mágneses indukció mértékegységei
A mágneses indukció SI-mértékegysége a Tesla (T). Egy Tesla egyenlő egy Newton per Amper-méter (N/Am). Ez a definíció a Lorentz-erő képletéből származik:
1 \\, \\text\{T\} \= 1 \\, \\frac\{\\text\{N\}\}\{\\text\{A\} \\cdot \\text\{m\}\}
Egy másik, régebbi mértékegység a Gauss (G). A Tesla és a Gauss közötti kapcsolat a következő:
1 \\, \\text\{T\} \= 10^4 \\, \\text\{G\}
A gyakorlatban mindkét egységet használják, de a tudományos közösségben a Tesla az elfogadottabb SI-egység.
Példák a tipikus mágneses indukció értékekre
- A Föld mágneses tere a felszín közelében: kb. 10^\{\-4\} T (0.5 Gauss körül).
- Egy hűtőmágnes: kb. 10^\{\-2\} T (100 Gauss körül).
- Egy erős ipari mágnes: néhány Tesla.
- Egy orvosi MRI készülék mágneses tere: tipikusan 1.5-3 Tesla, de léteznek erősebb rendszerek is.


A mágneses indukció forrásai
A mágneses indukció, azaz a mágneses tér különböző forrásokból származhat. A két fő forrás az állandó mágnesek és az elektromos áram.
Állandó mágnesek
Az állandó mágnesek olyan anyagok, amelyek atomi szinten rendezett mágneses dipólusokkal rendelkeznek. Ezek a dipólusok eredetileg az elektronok spinjéből és keringéséből származnak. Bizonyos anyagokban, mint például a ferromágneses anyagokban (pl. vas, nikkel, kobalt), ezek a dipólusok spontán módon egy irányba rendeződhetnek, még külső mágneses tér hiányában is, létrehozva egy makroszkopikus mágneses teret. Az állandó mágneseknek van egy északi és egy déli pólusuk, és a mágneses tér vonalai az északi pólustól indulnak ki, és a déli pólusban végződnek a mágnesen kívül, míg a mágnesen belül a déli pólustól az északi pólus felé haladnak.
Elektromos áram
Egy másik, rendkívül fontos forrása a mágneses indukciónak az elektromos áram. Amikor elektromos töltések mozognak, mágneses teret hoznak létre maguk körül. Ezt a jelenséget írja le az Ampère-törvény. Egy egyenes, hosszú vezető körül, amelyben I áram folyik, a mágneses indukció (\\mathbf\{B\}) körkörös vonalak mentén helyezkedik el a vezető körül, és a nagysága a következőképpen adható meg:
B \= \\frac\{\\mu\_0 I\}\{2 \\pi r\}
ahol \\mu\_0 a vákuum permeabilitása (4\\pi \\times 10^\{\-7\} \\, \\text\{T\} \\cdot \\text\{m/A\}), I az áram erőssége, és r a vezetőtől mért távolság. A mágneses tér irányát itt is a jobbkéz-szabállyal határozhatjuk meg: ha a hüvelykujjunk az áram irányába mutat, akkor a begörbülő ujjaink a mágneses tér vonalainak irányát jelzik.
Elektromágnesek
Az elektromos áram mágneses hatását kihasználva hozhatunk létre elektromágneseket. Egy tekercsbe (szolenoidba) vezetett elektromos áram sokkal erősebb és irányíthatóbb mágneses teret generál, mint egy egyenes vezető. A szolenoid belsejében a mágneses tér közel homogén, és a nagysága arányos a tekercs menetszámával, az áram erősségével és fordítottan arányos a tekercs hosszával (hosszú szolenoid esetén). Az elektromágnesek kulcsfontosságúak számos technológiai alkalmazásban, a reléktől kezdve az MRI-berendezésekig.

A mágneses indukció fontos törvényei
Számos alapvető fizikai törvény írja le a mágneses indukció viselkedését és kapcsolatát más fizikai mennyiségekkel.

Faraday indukciós törvénye
A Faraday indukciós törvénye az egyik legfontosabb törvény az elektromágnesességben. Kimondja, hogy ha egy zárt vezetőhurokban megváltozik a mágneses fluxus, akkor a hurokban elektromotoros erő (EMF) indukálódik. Az indukált EMF nagysága egyenlő a mágneses fluxus időbeli változásának sebességével:
\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}
A negatív előjel a Lenz-törvényt tükrözi, amely kimondja, hogy az indukált áram (és az általa létrehozott mágneses tér) olyan irányú, hogy akadályozza a fluxus változását, amely létrehozta.
Lenz törvénye
Ahogy említettük, a Lenz törvénye kiegészíti Faraday törvényét azáltal, hogy megadja az indukált áram irányát. Ha egy mágnes közeledik egy tekercshez, az indukált áram olyan mágneses teret hoz létre, amely taszítja a mágnest. Ha a mágnes távolodik, az indukált áram olyan mágneses teret hoz létre, amely vonzza a mágnest. Ez az “ellenállás” a fluxus változásával szemben az energia megmaradásának elvéből következik.
Gauss törvénye a mágnesességre
A Gauss törvénye a mágnesességre kimondja, hogy nincsenek mágneses monopólusok, azaz nincsenek olyan “mágneses töltések”, amelyekből a mágneses térvonalak kiindulnának vagy amelyekben végződnének. Matematikailag ezt úgy fejezzük ki, hogy egy zárt felületen átmenő mágneses fluxus mindig nulla:
\\oint \\mathbf\{B\} \\cdot d\\mathbf\{A\} \= 0
Ez azt jelenti, hogy a mágneses térvonalak mindig zárt hurkokat alkotnak.
Ampère törvénye (kibővítve Maxwell korrekciójával)
Az Ampère törvénye eredetileg az elektromos áram és az általa létrehozott mágneses tér közötti kapcsolatot írta le:
\\oint \\mathbf\{B\} \\cdot d\\mathbf\{l\} \= \\mu\_0 I\_\{enc\}
ahol az integrál egy zárt görbe mentén történik, és I\_\{enc\} a görbe által körülvett áram. Maxwell kiegészítette ezt a törvényt a eltolási áram fogalmával, hogy figyelembe vegye a változó elektromos mezők mágneses hatását is. A Maxwell-Ampère törvény kibővített formája:
\\oint \\mathbf\{B\} \\cdot d\\mathbf\{l\} \= \\mu\_0 \\left\(I\_\{enc\} \+ \\epsilon\_0 \\frac\{d\\Phi\_E\}\{dt\}\\right\)
ahol \\epsilon\_0 a vákuum permittivitása, és \\frac\{d\\Phi\_E\}\{dt\} az elektromos fluxus időbeli változásának sebessége.
Kísérletek a mágneses indukció bemutatására
A mágneses indukció jelensége látványos kísérletekkel demonstrálható, amelyek segítenek a fogalom intuitív megértésében.
Mágnes mozgatása tekercsben
Egy egyszerű, de szemléletes kísérlet, ha egy állandó mágnest mozgatunk egy tekercs belsejében vagy annak közelében. Ha a mágnest a tekercsbe toljuk, a tekercsben feszültség indukálódik, és ha egy zárt áramkör részét képezi a tekercs, akkor áram is folyik. Amikor a mágnes áll, nincs indukált feszültség vagy áram. Ha a mágnest kihúzzuk a tekercsből, ismét feszültség indukálódik, de az ellenkező polaritással, ami fordított irányú áramot eredményez.
Két tekercs kísérlete
Egy másik klasszikus kísérlet két egymás közelében elhelyezett tekercset használ. Ha az egyik tekercsben (primer tekercs) változtatjuk az áramot (például be- vagy kikapcsoljuk, vagy a nagyságát változtatjuk), akkor a változó mágneses fluxus a másik tekercsen (szekunder tekercs) keresztül is áthalad, és abban feszültséget indukál. Ez az elv áll a transzformátorok működésének hátterében.
A mágneses indukció alkalmazásai
A mágneses indukció elvén számos nélkülözhetetlen technológiai eszköz és berendezés működik.
Elektromos generátorok
Az elektromos generátorok mechanikai energiát alakítanak át elektromos energiává a mágneses indukció segítségével. Egy vezetőhurkot (vagy tekercset) egy mágneses térben forgatnak, vagy egy mágneses teret forgatnak egy álló vezetőhurok körül. Mindkét esetben a vezetőhurkon áthaladó mágneses fluxus változik, ami elektromotoros erőt (feszültséget) indukál a hurokban. Ez az