A Mágneses Indukció Képlete: Mélyreható Elemzés és Alkalmazások

A Mágneses Indukció Alapjai

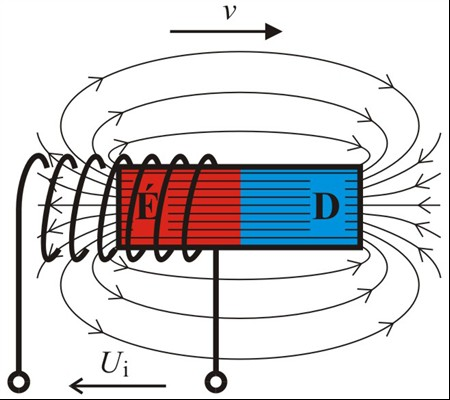
A mágneses indukció egy alapvető jelenség az elektromágnesség területén, amely leírja, hogyan hoz létre egy változó mágneses tér elektromos teret. Ez a kölcsönhatás képezi számos modern technológia működésének alapját, a generátoroktól a transzformátorokig. Ahhoz, hogy teljes mértékben megértsük a mágneses indukció képletét, először is tisztáznunk kell a kapcsolódó alapfogalmakat, mint például a mágneses fluxus és Faraday törvénye.

A Mágneses Fluxus Fogalma

A mágneses fluxus (\\Phi\_B) egy adott felületen áthaladó mágneses tér mennyiségének mértéke. Képzeljünk el egy mágneses teret, amelyet mágneses térvonalakkal ábrázolunk. A mágneses fluxus arányos azzal a vonalszámmal, amely egy adott felületet áthalad. Matematikailag a mágneses fluxust a következőképpen definiáljuk:

\\Phi\_B \= \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}

Ahol \\mathbf\{B\} a mágneses indukció vektor (más néven mágneses tér sűrűség), és d\\mathbf\{A\} a felület egy infiniteszimális elemének vektoros területe, amelynek iránya merőleges a felületre. Ha a mágneses tér homogén a felületen, és a mágneses tér vektor párhuzamos a felület normálisával, akkor a képlet egyszerűsödik:

\\Phi\_B \= BA \\cos\{\\theta\}

Ahol B a mágneses tér erőssége, A a felület területe, és \\theta a mágneses tér vektor és a felület normálisának szöge. A mágneses fluxus mértékegysége a Weber (Wb), ahol 1 Wb = 1 Tm$^2$ (Tesla-négyzetméter).

Faraday Indukciós Törvénye

Michael Faraday kísérletei során fedezte fel az elektromágneses indukció alapvető törvényét. Faraday törvénye kimondja, hogy egy zárt áramkörben indukált elektromotoros erő (EMF, \\mathcal\{E\}) egyenlő a mágneses fluxus időbeli változásának negatívjával az áramkörön keresztül:

\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}

Ez a képlet a mágneses indukció képletének központi eleme. A negatív előjel Lenz törvényét tükrözi, amely szerint az indukált áram iránya olyan, hogy mágneses terével akadályozza a fluxus változását, amely létrehozta őt.

Az Indukált Elektromotoros Erő Részletesebben

Az indukált elektromotoros erő (EMF) valójában egy potenciálkülönbség, amely egy vezetőben vagy áramkörben jön létre a változó mágneses fluxus hatására. Ez az EMF képes áramot hajtani, ha az áramkör zárt. A Faraday-féle indukciós törvény kvantitatív kapcsolatot teremt a változó mágneses fluxus és az indukált EMF között.

Lenz Törvényének Szerepe

Mint említettük, a Faraday-féle indukciós törvényben szereplő negatív előjel a Lenz-törvény következménye. Lenz törvénye elengedhetetlen az indukált áram és az indukált mágneses tér irányának meghatározásához. Egyszerűen fogalmazva, az indukált áram olyan irányú, hogy az általa létrehozott mágneses tér ellentétes a fluxus változásával, amely az indukciót okozta. Ez az elv biztosítja az energiamegmaradást az elektromágneses indukciós folyamatokban.

A Mágneses Indukció Képletének Levezetése Mozgó Vezető Esetén

Tekintsünk egy l hosszúságú vezetőt, amely egy homogén \\mathbf\{B\} mágneses térben v sebességgel mozog, úgy hogy a sebességvektor merőleges a mágneses tér vektorra és a vezetőre is. A vezetőben lévő töltött részecskékre (például elektronokra) ható mágneses erő a Lorentz-erő:

\\mathbf\{F\} \= q\(\\mathbf\{v\} \\times \\mathbf\{B\}\)

Ahol q a töltés. Az elektronokra ható erő iránya a jobbkéz-szabály szerint meghatározható. Ennek az erőnek a hatására a töltések a vezető mentén elmozdulnak, ami egy elektromos teret hoz létre a vezetőben. Amikor a mágneses erő által létrehozott elektromos erő egyensúlyba kerül a töltésekre ható mágneses erővel, egy állandó elektromos tér alakul ki.

Az indukált elektromotoros erő a vezető két vége közötti potenciálkülönbség:

\\mathcal\{E\} \= \\int \(\\mathbf\{v\} \\times \\mathbf\{B\}\) \\cdot d\\mathbf\{l\}

Ha \\mathbf\{v\}, \\mathbf\{B\} és d\\mathbf\{l\} páronként merőlegesek egymásra, akkor ez leegyszerűsödik:

\\mathcal\{E\} \= Blv

Ez a képlet azt mutatja, hogy egy mozgó vezetőben indukált EMF arányos a mágneses tér erősségével, a vezető hosszával és a sebességével.

A Mágneses Indukció Képletének Levezetése Változó Mágneses Tér Esetén

Most vizsgáljuk meg azt az esetet, amikor egy rögzített áramkörben változik a mágneses fluxus. Faraday törvénye közvetlenül megadja az indukált EMF-et:

\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}

Ha a mágneses tér időben változik, de a felület állandó, akkor a fluxus időbeli deriváltja a mágneses tér időbeli deriváltjával függ össze:

\\frac\{d\\Phi\_B\}\{dt\} \= \\frac\{d\}\{dt\} \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\} \= \\int \\frac\{\\partial \\mathbf\{B\}\}\{\\partial t\} \\cdot d\\mathbf\{A\}

Így az indukált EMF:

\\mathcal\{E\} \= \-\\int \\frac\{\\partial \\mathbf\{B\}\}\{\\partial t\} \\cdot d\\mathbf\{A\}

Ez a forma a mágneses indukció képletének egy általánosabb megközelítése, amely a változó mágneses tér hatására létrejövő elektromos teret írja le.

A Mágneses Indukció és az Elektromos Tér kapcsolata: Faraday-Maxwell törvény

A Faraday-féle indukciós törvény a Maxwell-egyenletek egyik alapvető formája, amely összekapcsolja a változó mágneses teret az elektromos térrel. Integrális formában a Faraday-Maxwell törvény így szól:

\\oint \\mathbf\{E\} \\cdot d\\mathbf\{l\} \= \-\\frac\{d\}\{dt\} \\iint\_S \\mathbf\{B\} \\cdot d\\mathbf\{A\} \= \-\\frac\{d\\Phi\_B\}\{dt\}

Ahol a bal oldalon az elektromos tér vonalintegrálja egy zárt görbe mentén, a jobb oldalon pedig a mágneses fluxus időbeli változása a görbe által határolt felületen keresztül látható. Ez az egyenlet azt fejezi ki, hogy egy változó mágneses fluxus elektromos teret indukál.

Differenciális formában a Faraday-Maxwell törvény:

\\nabla \\times \\mathbf\{E\} \= \-\\frac\{\\partial \\mathbf\{B\}\}\{\\partial t\}

Ez a forma lokális kapcsolatot ír le a térben az elektromos tér rotációja és a mágneses tér időbeli változása között.

Az Induktivitás Fogalma

Az induktivitás (L) egy áramkör azon tulajdonsága, amely ellenáll az áram változásának önindukció vagy kölcsönös indukció révén. Ha egy áramkörben áram folyik, mágneses fluxust hoz létre, amely arányos az árammal:

\\Phi\_B \= LI

Ahol I az áram. Ha az áram időben változik, a mágneses fluxus is változik, ami Faraday törvénye szerint elektromotoros erőt indukál az áramkörben:

\\mathcal\{E\} \= \-L \\frac\{dI\}\{dt\}

Ez az önindukció jelensége. Az induktivitás mértékegysége a Henry (H).

Kölcsönös Indukció

A kölcsönös indukció akkor lép fel, ha egy áramkörben változó áram egy másik közeli áramkörben is elektromotoros erőt indukál a két áramkör által megosztott mágneses fluxus változása miatt. Ha az 1. áramkörben I\_1 áram folyik, a 2. áramkörben létrejövő mágneses fluxus \\Phi\_\{21\} \= M\_\{21\}I\_1, ahol M\_\{21\} a 2. áramkör 1. áramkörre vonatkozó kölcsönös induktivitása. A 2. áramkörben indukált EMF:

\\mathcal\{E\}\_2 \= \-\\frac\{d\\Phi\_\{21\}\}\{dt\} \= \-M\_\{21\} \\frac\{dI\_1\}\{dt\}

Hasonlóképpen, az 1. áramkörben az áram változása a 2. áramkörben fluxust hoz létre, \\Phi\_\{12\} \= M\_\{12\}I\_2, és az 1. áramkörben indukált EMF:

\\mathcal\{E\}\_1 \= \-\\frac\{d\\Phi\_\{12\}\}\{dt\} \= \-M\_\{12\} \\frac\{dI\_2\}\{dt\}

M\_\{12\} \= M\_\{21\} \= M, amelyet egyszerűen kölcsönös induktivitásnak nevezünk.

A Mágneses Indukció Alkalmazásai

A mágneses indukció elve számos technológiai alkalmazás alapját képezi:

Elektromos Generátorok

A generátorok mechanikai energiát alakítanak át elektromos energiává a mágneses indukció segítségével. Egy tekercset vagy vezetőt egy mágneses térben forgatnak, ami a mágneses fluxus változását okozza a tekercsen keresztül, indukálva ezzel egy elektromotoros erőt és áramot.

Transzformátorok

A transzformátorok a kölcsönös indukció elvén működnek. Két vagy több tekercsből állnak, amelyek egy közös mágneses magra vannak feltekercselve. Egyik tekercsben (primer tekercs) változó áramot vezetnek, ami változó mágneses fluxust hoz létre a magban. Ez a változó fluxus elektromotoros erőt indukál a másik tekercsben (szekunder tekercs), lehetővé téve a feszültség és az áram átalakítását.

Indukciós Főzés

Az indukciós főzőlapok változó mágneses teret használnak, hogy áramot indukáljanak a főzőedény aljában. Ez az indukált áram (örvényáram) felmelegíti az edényt, így főzve meg az ételt.

Elektromágneses Fékek

Bizonyos járművekben elektromágneses fékeket használnak, amelyek a mágneses indukció elvén működnek. A mozgó kerekekkel együtt forgó féktárcsába mágneses teret hoznak létre, ami örvényáramokat indukál a tárcsában. Ezek az áramok mágneses teret hoznak létre, amely ellentétes az eredetivel, így fékező hatást eredményez.

Vezeték Nélküli Töltés

A vezeték nélküli töltési technológiák, mint például a mobiltelefonok töltése, szintén a mágneses indukciót használják. Egy adótekercsben váltakozó áramot vezetnek, ami változó mágneses teret hoz létre. Ez a tér elektromos áramot indukál a vevőtekercsben, amely a töltendő eszközben található.

Példák a Mágneses Indukció Képletének Alkalmazására

Példa 1: Mozgó vezető

Egy 0.5 m hosszú vezető 2 T erősségű mágneses térben mozog 10 m/s sebességgel, úgy hogy a sebesség merőleges a mágneses térre és a vezetőre. Számítsuk ki az indukált elektromotoros erőt!

Használjuk a \\mathcal\{E\} \= Blv képletet:

\\mathcal\{E\} \= \(2 \\, \\text\{T\}\) \\times \(0\.5 \\, \\text\{m\}\) \\times \(10 \\, \\text\{m/s\}\) \= 10 \\, \\text\{V\}

Tehát az indukált elektromotoros erő 10 V.

Példa 2: Változó mágneses fluxus

Egy 0.1 m