A mágneses indukcióvektor: Átfogó tanulmány a mágneses tér alapvető fogalmáról

A mágneses indukcióvektor, amelyet gyakran \\mathbf\{B\}-vel jelölünk, a mágneses tér egyik legfontosabb és legmeghatározóbb mennyisége. Ez a vektormennyiség nem csupán a mágneses tér erősségét írja le egy adott pontban, hanem annak irányát is. A mágneses indukcióvektor megértése elengedhetetlen az elektromágnesség jelenségeinek mélyreható tanulmányozásához, kezdve az egyszerű mágneses erőhatásoktól egészen a komplex elektromágneses hullámokig és a modern technológiai alkalmazásokig.

A mágneses indukcióvektor definíciója és alapjai

A mágneses indukcióvektor formális definíciója a Lorentz-erőn keresztül történik. Ha egy q töltésű részecske \\mathbf\{v\} sebességgel mozog egy olyan térben, ahol mind elektromos (\\mathbf\{E\}) és mágneses (\\mathbf\{B\}) tér is jelen van, akkor a részecskére ható teljes erő, a Lorentz-erő a következőképpen adható meg:

$$ \mathbf{F} = q(\mathbf{E} + \mathbf{v} \times \mathbf{B}) $$

Ebben az egyenletben a \\mathbf\{v\} \\times \\mathbf\{B\} tag képviseli a mágneses erő komponensét. Látható, hogy a mágneses erő függ a töltés sebességétől és a mágneses indukcióvektor kereszttermékétől. Ez azt jelenti, hogy a mágneses erő mindig merőleges a töltés sebességére és a mágneses indukcióvektorra is.

A mágneses indukcióvektor mértékegysége

A mágneses indukcióvektor SI-mértékegysége a tesla (T). Egy tesla az a mágneses indukció, amely egy 1 coulomb töltésű, 1 méter per szekundum sebességgel mozgó részecskére 1 newton nagyságú, a sebességére és a mágneses térre is merőleges erőt fejt ki. Másik gyakran használt mértékegység a gauss (G), ahol 1 T = 10 000 G.

A mágneses indukcióvektor tulajdonságai

A mágneses indukcióvektornak számos fontos tulajdonsága van, amelyek elengedhetetlenek a mágneses jelenségek megértéséhez:

• Ez egy vektormennyiség, ami azt jelenti, hogy mind nagysága, mind iránya van.
• A mágneses erő, amelyet egy mozgó töltésre kifejt, arányos a mágneses indukcióvektor nagyságával.

• A mágneses erő iránya merőleges mind a töltés sebességére, mind a mágneses indukcióvektorra.
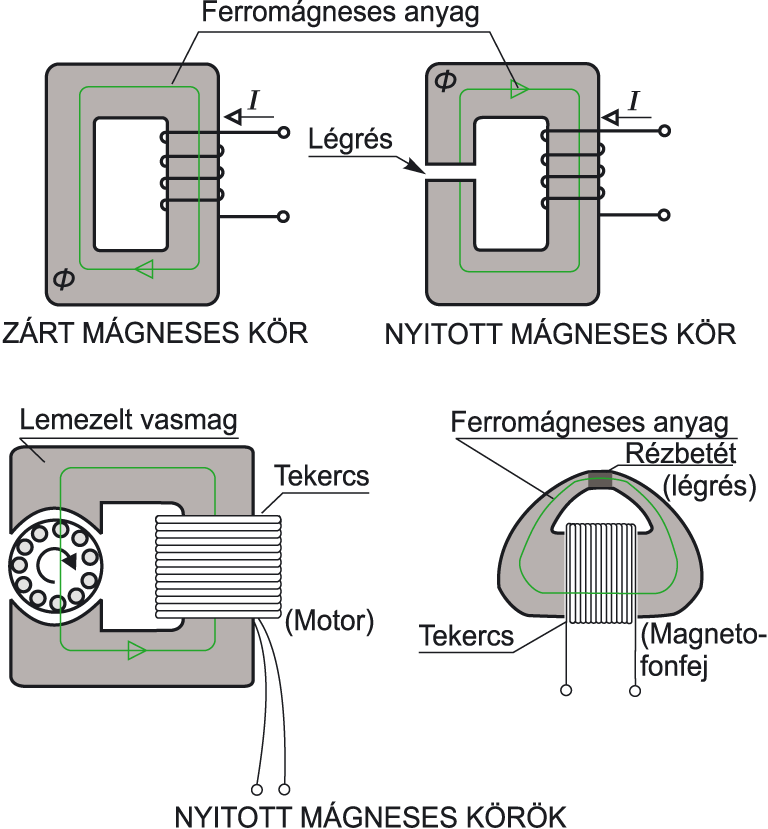
• A mágneses indukcióvonalak zárt görbéket alkotnak; nincsenek mágneses monopólusok. Ez a tény a Maxwell-egyenletek egyik alapvető megállapítása.
• A mágneses indukcióvektor szorosan összefügg a mágneses fluxussal. A mágneses fluxus (\\Phi\_B) egy adott felületen áthaladó mágneses indukcióvonalak számának mértéke, amelyet a következőképpen definiálunk:
  

  $$ \Phi_B = \int \mathbf{B} \cdot d\mathbf{A} $$

  ahol d\\mathbf\{A\} a felület infinitezimális vektoros eleme.

A mágneses indukcióvonalak

A mágneses indukcióvonalak képzeletbeli vonalak, amelyek a mágneses tér irányát szemléltetik. Ezek a vonalak a mágneses indukcióvektor irányába mutatnak minden pontban. Fontos megjegyezni, hogy a mágneses indukcióvonalak mindig zárt hurkokat alkotnak, ami a mágneses monopólusok hiányának következménye. A vonalak sűrűsége egy adott területen arányos a mágneses indukcióvektor nagyságával azon a területen.

A mágneses indukcióvektor forrásai

A mágneses indukcióvektort mozgó elektromos töltések és mágneses anyagok hozhatják létre.

Áramjárta vezetők

Egy áramjárta vezető körül mágneses tér alakul ki. Az áram által létrehozott mágneses indukcióvektor nagysága és iránya az áram erősségétől, a vezető geometriájától és a megfigyelési pont helyzetétől függ. A Biot-Savart törvény adja meg az infinitezimális áramszegmens által létrehozott mágneses indukcióvektort:

$$ d\mathbf{B} = \frac{\mu_0}{4\pi} \frac{I d\mathbf{l} \times \mathbf{r}}{r^3} $$

ahol I az áram erőssége, d\\mathbf\{l\} az áramszegmens vektoros hossza, \\mathbf\{r\} a helyvektor az áramszegmenstől a megfigyelési pontig, r a \\mathbf\{r\} vektor nagysága, és \\mu\_0 a vákuum permeabilitása (4\\pi \\times 10^\{\-7\} \\, \\text\{T m/A\}).

Példa: Egyenes áramjárta vezető mágneses indukcióvektora

Egy hosszú, egyenes áramjárta vezető körül a mágneses indukcióvonalak koncentrikus körök, amelyek középpontja a vezető tengelyében van, és a síkjuk merőleges a vezetőre. A mágneses indukcióvektor nagysága egy r távolságra a vezetőtől a következőképpen adható meg:

$$ B = \frac{\mu_0 I}{2\pi r} $$

Az irányát a jobbkéz-szabály adja meg: ha a jobb hüvelykujjunk az áram irányába mutat, akkor a begörbülő ujjaink a mágneses indukcióvektor irányát jelzik.

Mágneses anyagok

A mágneses anyagok, mint például a ferromágneses anyagok (vas, nikkel, kobalt), saját belső mágneses tereket hozhatnak létre atomi szinten lévő elektronok spinjének és pályamozgásának köszönhetően. Ezek az atomi dipólusmomentumok rendeződhetnek külső mágneses tér hatására, vagy akár spontán módon is, létrehozva egy makroszkopikus mágneses teret. A mágneses indukcióvektor egy mágneses anyagban függ a külső mágneses tértől és az anyag magnetizációjától (\\mathbf\{M\}):

$$ \mathbf{B} = \mu_0 (\mathbf{H} + \mathbf{M}) $$

ahol \\mathbf\{H\} a mágneses térerősség.

A mágneses indukcióvektor mérése

A mágneses indukcióvektor mérésére különböző módszereket alkalmaznak, attól függően, hogy milyen erősségű és jellegű a mérendő mágneses tér.

Hall-effektus szenzorok

A Hall-effektus egy olyan jelenség, amely során egy áramjárta vezetőben vagy félvezetőben, a vezetőre merőleges mágneses tér hatására, a töltéshordozók elhajlanak, és a vezető keresztirányában feszültségkülönbség (Hall-feszültség) jön létre. A Hall-feszültség nagysága arányos a mágneses indukcióvektor erősségével, így a Hall-effektus szenzorok széles körben használatosak mágneses tér mérésére.

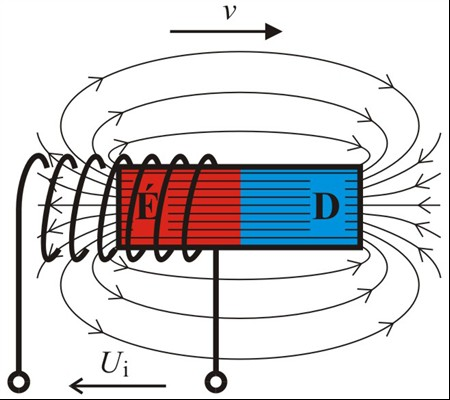
Tekercsek és Faraday törvénye

A Faraday-féle indukciós törvény kimondja, hogy egy zárt vezetőben indukált elektromotoros erő arányos a vezetőt körülvevő mágneses fluxus időbeli változásának sebességével:

$$ \mathcal{E} = -\frac{d\Phi_B}{dt} $$

Ezt a törvényt felhasználva, egy mérőtekercsbe indukált feszültség mérésével következtethetünk a mágneses tér erősségére. Ha a mágneses tér változik, vagy ha a tekercs mozog a mágneses térben, mágneses fluxus változik, ami indukált feszültséget eredményez. A mért feszültségből, a tekercs geometriájának ismeretében, meghatározható a mágneses indukcióvektor.

SQUID-ok (szupravezető kvantum interferencia eszközök)

A SQUID-ok rendkívül érzékeny magnetométerek, amelyek a szupravezetés kvantummechanikai tulajdonságait használják ki a nagyon gyenge mágneses terek mérésére. Alkalmazásuk kiterjed a geofizikától az orvosi diagnosztikáig (pl. magnetoenkefalográfia).

A mágneses indukcióvektor és a Maxwell-egyenletek

A mágneses indukcióvektor központi szerepet játszik a Maxwell-egyenletekben, amelyek az elektromágnesség alapvető törvényeit foglalják össze:

1. Gauss törvénye az elektromosságról: \\nabla \\cdot \\mathbf\{E\} \= \\frac\{\\rho\}\{\\epsilon\_0\}
2. Gauss törvénye a mágnességről: \\nabla \\cdot \\mathbf\{B\} \= 0 (a mágneses monopólusok hiánya)
3. Faraday indukciós törvénye: \\nabla \\times \\mathbf\{E\} \= \-\\frac\{\\partial \\mathbf\{B\}\}\{\\partial t\}
4. Ampère-Maxwell törvény: \\nabla \\times \\mathbf\{B\} \= \\mu\_0 \\left\( \\mathbf\{J\} \+ \\epsilon\_0 \\frac\{\\partial \\mathbf\{E\}\}\{\\partial t\} \\right\)

A második Maxwell-egyenlet, \\nabla \\cdot \\mathbf\{B\} \= 0, kifejezi azt a tényt, hogy nincsenek mágneses monopólusok, és a mágneses indukcióvonalak mindig zártak. A harmadik egyenlet, a Faraday-törvény, leírja, hogy a változó mágneses tér elektromos teret indukál. A negyedik egyenlet, az Ampère-Maxwell törvény, azt mutatja meg, hogy az elektromos áram és a változó elektromos tér mágneses teret hoz létre.

A mágneses indukcióvektor gyakorlati alkalmazásai

A mágneses indukcióvektor megértése és mérése számos technológiai alkalmazás alapját képezi:

• Elektromos motorok és generátorok: Ezek az eszközök a mágneses erő elvén működnek, amely egy áramjárta vezetőre hat mágneses térben.
• Transzformátorok: A Faraday-féle indukció elvén működnek, ahol egy változó mágneses fluxus elektromos feszültséget indukál egy másik tekercsben.
• Adatrögzítés: A merevlemezek és más mágneses adathordozók a mágneses domének irányának megváltoztatásával tárolják az információt.
• Orvosi képalkotás (MRI): A mágneses rezonancia képalkotás erős mágneses tereket és rádióhullámokat használ a test belső szerkezetének részletes képeinek létrehozására.
• Navigáció: A Föld mágneses terét iránytűk és más navigációs eszközök használják az irány meghatározására.
• Tudományos kutatás: A mágneses terek tanulmányozása elengedhetetlen a plazmafizikában, az asztrofizikában és az anyagtudományban.

A mágneses indukcióvektor szerepe az MRI-ben

A mágneses rezonancia képalkotás (MRI) egy orvosi képalkotó eljárás, amely erős mágneses tereket használ a test belsejének részletes képeinek létrehozására. A folyamat során a páciens egy erős, statikus mágneses térbe kerül, amelynek mágneses indukcióvektora tipikusan 1,5 és 7 tesla között van. Ez a mágneses tér hatására a testben lévő vízmolekulák hidrogénatomjainak protonjai (amelyeknek saját mágneses momentumuk van) a mágneses tér irányába rendeződnek. Ezután rádiófrekvenciás impulzusokat bocsátanak ki, amelyek rezonanciába hozzák a protonokat. Amikor az impulzusok megszűnnek, a protonok visszatérnek eredeti állapotukba, miközben rádióhullámokat bocsátanak ki. Ezeket a hullámokat érzékelik a MRI-szkenner detektorai, és a jelekből számítógépes algoritmusok segítségével részletes képeket alkotnak a test belső szerkezetéről. A mágneses indukcióvektor erőssége és homogenitása kulcsfontosságú a kiváló minőségű MRI-képek eléréséhez.

A mágneses indukcióvektor a geofizikában

A Földnek is van saját mágneses tere, amelyet elsősorban a Föld külső magjában lévő olvadt vas áramlásai generálnak (geodinamo). A Föld mágneses indukcióvektora a felszínen körülbelül 25 és 65 mikrotesla között változik. Ez a mágneses tér fontos szerepet játszik a navigációban (iránytűk), védelmet nyújt a káros kozmikus sugárzás és a napszél ellen (magnetoszféra), és információkat hordoz a Föld múltbeli mágneses teréről (paleomágnesség). A geofizikusok a mágneses indukcióvektor mérésével és elemzésével tanulmányozzák a Föld belső szerkezetét, a kőzetek mágneses tulajdonságait és a mágneses tér időbeli változásait.

Összefoglalás