Magneses Megosztas
A Mágneses Megosztás Átfogó Tanulmánya: Elmélet, Alkalmazások és Jövőbeli Lehetőségek
A mágneses megosztás egy lenyűgöző jelenség, amely a fizika alapvető erői közé tartozó mágnesesség elvén alapszik. Ez a fogalom sokkal többet foglal magában, mint csupán két mágnes vonzását vagy taszítását. A modern tudomány és technológia számos területén kulcsszerepet játszik, az energiaátviteltől kezdve az adatmentésen át a legkülönfélébb szenzorok működéséig. Ebben a részletes elemzésben mélyrehatóan feltárjuk a mágneses megosztás elméleti alapjait, a gyakorlati alkalmazásainak széles spektrumát, a legújabb kutatási eredményeket és a jövőbeli potenciálját.
A Mágnesesség Alapjai és a Mágneses Megosztás Elve
A mágnesesség egy olyan fizikai jelenség, amelyet a mozgó elektromos töltések hoznak létre. Az atomok elektronjainak mozgása és a spinjük is mágneses momentumot eredményez. Az anyagok mágneses tulajdonságai attól függenek, hogy ezek a mikroszkopikus mágneses momentumok hogyan rendeződnek. A mágneses megosztás lényegében azt jelenti, hogy egy mágneses tér hatással van egy másik mágneses objektumra, vagy egy mágneses objektum hatással van egy mágneses térre. Ez a kölcsönhatás erőket és nyomatékokat eredményezhet.
A Mágneses Tér és annak Jellemzői
A mágneses tér egy vektormező, amely a mozgó elektromos töltések és a mágneses momentummal rendelkező anyagok körül létezik. A mágneses teret általában a \\mathbf\{B\} szimbólummal jelöljük, és mértékegysége a Tesla (T). A mágneses tér erősségét és irányát a tér minden pontjában definiáljuk. A mágneses tér vonalainak képzeletbeli görbéi segítenek a tér vizualizálásában. Ezek a vonalak a mágnes északi pólusától indulnak és a déli pólusánál érnek véget, a mágnes belsejében pedig zárt hurkokat alkotnak. A mágneses tér erőssége arányos a mágneses térvonalak sűrűségével.
A Biot-Savart Törvény

A Biot-Savart törvény egy alapvető fizikai törvény, amely leírja, hogy egy állandó elektromos áram hogyan hoz létre mágneses teret. A törvény szerint egy I áramot vezető d\\mathbf\{l\} hosszúságú kis vezetőszegmens által egy \\mathbf\{r\} távolságra lévő pontban létrehozott d\\mathbf\{B\} mágneses tér a következőképpen számítható ki:
\\mathbf\{dB\} \= \\frac\{\\mu\_0\}\{4\\pi\} \\frac\{I d\\mathbf\{l\} \\times \\mathbf\{\\hat\{r\}\}\}\{r^2\}
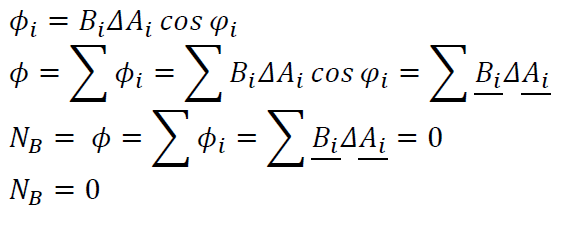
ahol \\mu\_0 a vákuum permeabilitása, és \\mathbf\{\\hat\{r\}\} az egységvektor a vezetőszegmenstől a megfigyelési pontig.
Az Ampère-féle Törvény
Az Ampère-féle törvény egy másik fontos összefüggés a mágnesesség területén, amely a mágneses tér és az áram közötti kapcsolatot írja le. Integrális formájában a törvény kimondja, hogy a mágneses tér vonalintegrálja egy zárt görbe mentén arányos a görbe által körülvett teljes árammal:
\\oint \\mathbf\{B\} \\cdot d\\mathbf\{l\} \= \\mu\_0 I\_\{enc\}
ahol I\_\{enc\} a zárt görbe által körülvett teljes áram.
A Mágneses Erő
Egy mozgó töltésre mágneses tér hatására erő hat. Ezt az erőt Lorentz-erőnek nevezzük, amelynek mágneses komponense a következőképpen adható meg:
\\mathbf\{F\}\_B \= q \(\\mathbf\{v\} \\times \\mathbf\{B\}\)
ahol q a töltés nagysága, \\mathbf\{v\} a töltés sebessége, és \\mathbf\{B\} a mágneses tér. Ez az erő mindig merőleges a töltés sebességére és a mágneses térre is, ezért nem végez munkát a töltésen, csupán megváltoztatja annak mozgásának irányát.
Erő áramvezetőre mágneses térben
Ha egy I áramot vezető vezető d\\mathbf\{l\} hosszúságú szegmense mágneses térben van, akkor erre a szegmensre ható mágneses erő:
d\\mathbf\{F\} \= I d\\mathbf\{l\} \\times \\mathbf\{B\}
Egy véges hosszúságú vezetőre ható teljes erő a fenti kifejezés integrálásával kapható meg a vezető mentén.
Erő két áramvezető között
Két párhuzamos, áramot vezető vezető egymásra mágneses erőt fejt ki. Ha az áramok azonos irányúak, az erők vonzóak, ha ellentétes irányúak, akkor taszítóak. Két hosszú, párhuzamos, d távolságra lévő vezető között, amelyeken I\_1 és I\_2 áram folyik, az egységnyi hosszra jutó erő:
\\frac\{F\}\{L\} \= \\frac\{\\mu\_0 I\_1 I\_2\}\{2\\pi d\}

Mágneses Momentum
A mágneses momentum egy olyan vektor mennyiség, amely egy objektum mágneses erősségét és irányát jellemzi. Egy áramhurok mágneses momentuma a hurok által bezárt terület és az áram szorzatával arányos, és iránya a jobbkéz-szabály szerint adódik:
\\mathbf\{\\mu\} \= I \\mathbf\{A\}
ahol I az áram a hurokban, és \\mathbf\{A\} a hurok által bezárt területvektor (irányát a jobbkéz-szabály adja meg).
Nyomaték mágneses térben lévő mágneses momentumra
Egy \\mathbf\{\\mu\} mágneses momentummal rendelkező objektumra, amely egy \\mathbf\{B\} mágneses térben található, ható nyomaték:
\\mathbf\{\\tau\} \= \\mathbf\{\\mu\} \\times \\mathbf\{B\}
Ez a nyomaték arra törekszik, hogy a mágneses momentumot a mágneses tér irányába forgassa.
A Mágneses Megosztás Alkalmazásai a Technikában
A mágneses megosztás elvén alapuló technológiák rendkívül széles körben elterjedtek a modern világban. Az alábbiakban néhány fontosabb alkalmazást részletezünk.
Elektromágneses Indukció és Energiaátvitel
Az elektromágneses indukció jelensége, amelyet Faraday fedezett fel, alapvető fontosságú az elektromos energia termelésében és átvitelében. Ha egy mágneses tér változik egy vezető hurok környezetében, vagy ha egy vezető hurok mozog egy mágneses térben, akkor a hurokban elektromotoros erő (EMF) indukálódik. Ez az elv áll a transzformátorok és a generátorok működésének hátterében.
Transzformátorok
A transzformátorok olyan eszközök, amelyek elektromágneses indukció segítségével képesek váltakozó feszültséget egyik áramkörből egy másikba átalakítani anélkül, hogy a két áramkör között közvetlen elektromos kapcsolat lenne. Egy tipikus transzformátor két tekercsből (primer és szekunder) áll, amelyek egy közös vasmagra vannak feltekercselve. A primer tekercsben folyó váltakozó áram változó mágneses teret hoz létre a vasmagban, amely indukálja a feszültséget a szekunder tekercsben. A feszültségek aránya a tekercsek menetszámának arányával egyenlő:
\\frac\{V\_p\}\{V\_s\} \= \\frac\{N\_p\}\{N\_s\}
ahol V\_p a primer feszültség, V\_s a szekunder feszültség, N\_p a primer tekercs menetszáma, és N\_s a szekunder tekercs menetszáma.
Generátorok
Az elektromos generátorok mechanikai energiát alakítanak át elektromos energiává az elektromágneses indukció elvén. A legegyszerűbb generátor egy mágneses térben forgó vezető hurkot tartalmaz. A hurok mozgása a mágneses téren keresztül változó mágneses fluxust eredményez a hurokban, ami elektromotoros erőt indukál. A modern erőművekben használt nagyméretű generátorok is ezen az elven működnek, ahol a forgómozgást gőz-, víz- vagy szélturbinák biztosítják.
Vezeték Nélküli Energiaátvitel
A mágneses megosztás lehetővé teszi a vezeték nélküli energiaátvitelt is. Két rezonáns tekercs között, amelyek azonos frekvencián rezonálnak, hatékony energiaátvitel valósulhat meg mágneses rezonancia révén. Ezt a technológiát alkalmazzák például okostelefonok vezeték nélküli töltésére és orvosi implantátumok energiaellátására.
Adatrögzítés és Adatvisszaolvasás
A mágneses megosztás kulcsszerepet játszik az adatok rögzítésében és visszaolvasásában is, különösen a hagyományos merevlemezek (HDD) esetében. Az adatok mágneses rétegen lévő apró mágneses domének polaritásának beállításával kerülnek rögzítésre. Az olvasófej, amely egy érzékeny mágneses szenzort tartalmaz, érzékeli ezeknek a doméneknek a mágneses terét, és így képes visszaolvasni a tárolt információt.

Merevlemezek (HDD)
A merevlemezek több forgó lemezből állnak, amelyek mágneses anyaggal vannak bevonva. A rögzítőfej elektromágnes segítségével képes lokálisan megváltoztatni a mágneses réteg polaritását, így bináris adatokat (0 és 1) tárolva. Az olvasófej egy induktív vagy magnetoreszisztív szenzor segítségével érzékeli a mágneses mező változásait a lemez forgása közben, és ezeket a változásokat elektromos jelekké alakítja, amelyek a tárolt adatoknak felelnek meg.
Mágneskártyák
A mágneskártyák, mint például a hitelkártyák és a beléptető kártyák, egy vékony mágneses csíkot tartalmaznak, amelyen az információ mágnesesen van kódolva. Amikor a kártyát egy olvasón keresztülhúzzák, az olvasófej érzékeli a mágneses csík mezőjét, és dekódolja az azon tárolt adatokat.
Szenzorok és Mérőeszközök
A mágneses megosztás elvén működő szenzorok és mérőeszközök rendkívül érzékenyek és sokoldalúak. Számos területen alkalmazzák őket, a navigációtól kezdve az ipari automatizáláson át az orvosi diagnosztikáig.
Hall-effektus Szenzorok
A Hall-effektus jelensége akkor lép fel, ha egy áramot vezető vezetőt egy mágneses térbe helyezünk, amely merőleges az áram irányára. Ekkor a vezetőben az áramra és a mágneses térre is merőleges irányban feszültség keletkezik, amelyet Hall-feszültségnek nevezünk. A Hall-effektus szenzorok ezt az elvet használják mágneses terek mérésére, pozícióérzékelésre és árammérésre.
Magnetoreszisztív Szenzorok
A magnetoreszisztív szenzorok olyan anyagok ellenállásának változását használják ki, amelyek mágneses tér hatására következnek be. Különböző típusai léteznek, mint például az anizotróp magnetoresztencia (AMR), a gigantikus magnetoresztencia (GMR) és a tunnelező magnetoresztencia (TMR). Ezek a szenzorok rendkívül érzékenyek és széles körben alkalmazzák őket például a merevlemezek olvasófejeiben, az autóiparban (sebesség- és pozícióérzékelők), valamint a biológiai és orvosi diagnosztikában.
SQUID-ok (Szupervezető Kvantum Interferencia Eszközök)
A SQUID-ok rendkívül érzékeny magnetométerek, amelyek a szupravezetés kvantummechanikai jelenségeit használják ki a rendkívül gyenge mágneses terek mérésére. Alkalmazzák őket például az orvosi képalkotásban (magnetoenkefalográfia, magnetokardiográfia), a geofizikában és az alapvető fizikai kutatásokban.
Mágneses Levitatáció
A mágneses levitatáció (maglev) egy olyan jelenség, amelyben egy objektumot mágneses erők segítségével lebegtetnek egy másik objektum felett anélkül, hogy fizikai érintkezés lenne közöttük. Ezt a technológiát alkalmazzák például a maglev vonatoknál, ahol a súrlódás csökkentésével nagy sebességek érhetők el.
Maglev Vonatok
A maglev vonatok erős mágneseket használnak mind a vonat, mind a pálya mentén. A vonatot a pálya fölé emelik és előre hajtják a mágneses erők. Mivel nincs fizikai érintkezés a vonat és a pálya között, a súrlódás jelentősen csökken, ami lehetővé teszi a nagyon nagy sebességek elérését és a csendesebb működést.
Orvosi Alkalmazások
A mágneses megosztás számos orvosi alkalmazásban is fontos szerepet játszik.
Mágneses Rezonancia Képalkotás (MRI)
A mágneses rezonancia képalkotás (MRI) egy orvosi képalkotó eljárás, amely erős mágneses teret és rádióhullámokat használ a test belső szerkezetének részletes képeinek létrehozására. Az MRI a testben lévő vízmolekulákban található hidrogénatomok magjainak mágneses tulajdonságait használja ki.