Mechanikai Energia
A Mechanikai Energia Átfogó Értelmezése és Alkalmazásai
A mechanikai energia a fizika egyik alapvető fogalma, amely egy test vagy rendszer mozgásával és helyzetével kapcsolatos energiát írja le. Lényegében ez az az energia, amely lehetővé teszi a munkavégzést mechanikai úton. A mechanikai energia megértése kulcsfontosságú a klasszikus mechanika, a mérnöki tudományok és számos természeti jelenség magyarázatához. Ebben a részletes cikkben feltárjuk a mechanikai energia különböző aspektusait, beleértve annak definícióját, fajtáit, a megmaradás törvényét, az átalakulás folyamatait és a gyakorlati alkalmazásokat a mindennapi életben és a technológiában.
A Mechanikai Energia Definíciója és Alapelvei
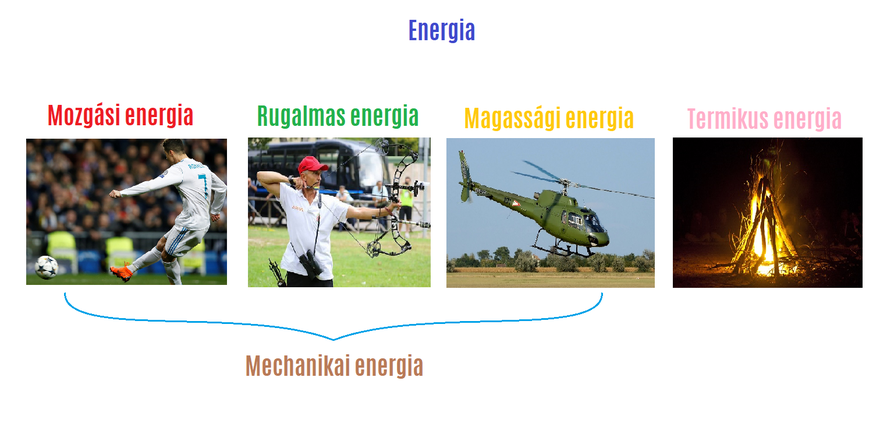
A mechanikai energia egy rendszer azon képessége, hogy munkát végezzen. Ez magában foglalja a mozgással kapcsolatos energiát, amelyet kinetikus energiának nevezünk, és a helyzettel vagy konfigurációval kapcsolatos energiát, amelyet potenciális energiának hívunk. Egy mechanikai rendszer teljes energiája a kinetikus és potenciális energiájának összege, feltéve, hogy nincsenek disszipatív erők, mint például a súrlódás, amelyek hővé alakítják az energiát. A mechanikai energia szorosan kapcsolódik az erő és a mozgás fogalmaihoz, mivel az erők munkát végezhetnek, megváltoztatva egy test mozgását és ezáltal a mechanikai energiáját.
A Kinetikus Energia Részletes Bemutatása
A kinetikus energia egy mozgó test energiája. Minél nagyobb egy test tömege és sebessége, annál nagyobb a kinetikus energiája. Matematikailag a kinetikus energia (E\_k) a következőképpen fejezhető ki:
\\displaystyle E\_k \= \\frac\{1\}\{2\}mv^2

ahol m a test tömege (kilogrammban), és v a test sebessége (méter per másodpercben). Ebből az egyenletből látható, hogy a sebesség négyzetesen befolyásolja a kinetikus energiát, ami azt jelenti, hogy a sebesség kétszeresére növelése négyszeresére növeli a kinetikus energiát azonos tömeg mellett. A kinetikus energia skaláris mennyiség, ami azt jelenti, hogy csak nagysága van, iránya nincs.
Példák a Kinetikus Energiára a Mindennapi Életben
Számos példát találhatunk a kinetikus energiára a mindennapi életben. Egy guruló labda kinetikus energiával rendelkezik a mozgása miatt. Egy repülő repülőgép, egy futó ember vagy egy áramló víz mind rendelkezik kinetikus energiával. Minél gyorsabban mozognak, annál nagyobb a kinetikus energiájuk. A kinetikus energia hasznosítható is, például egy szélmalom a szél kinetikus energiáját alakítja át mechanikai munkává, amely aztán elektromos áramot termelhet.
A Potenciális Energia Részletes Bemutatása
A potenciális energia egy test vagy rendszer helyzetéből vagy konfigurációjából adódó tárolt energia. Többféle formája létezik, attól függően, hogy milyen erőhatás hozza létre. A mechanikában leggyakrabban a gravitációs potenciális energiával és a rugalmas potenciális energiával találkozunk.
Gravitációs Potenciális Energia
A gravitációs potenciális energia egy testnek a gravitációs mezőben elfoglalt helyzetéből adódik. A Föld felszínén egy h magasságban lévő m tömegű test gravitációs potenciális energiája (E\_p) a következőképpen számítható ki:

\\displaystyle E\_p \= mgh
ahol g a gravitációs gyorsulás (a Földön körülbelül 9\.81 \\, m/s^2). Ebből az egyenletből látható, hogy minél magasabban van egy test, annál nagyobb a gravitációs potenciális energiája egy adott referencia szinthez képest (általában a Föld felszíne). A gravitációs potenciális energia is skaláris mennyiség.
Példák a Gravitációs Potenciális Energiára
Egy hegy tetején álló kő gravitációs potenciális energiával rendelkezik a magassága miatt. Ha a kő leesik, ez a potenciális energia kinetikus energiává alakul át. Egy víztározóban felgyülemlett víz szintén gravitációs potenciális energiával rendelkezik, amelyet a vízerőművek elektromos áram termelésére használnak fel, amikor a vizet leengedik turbinákon keresztül.
Rugalmas Potenciális Energia
A rugalmas potenciális energia egy rugalmasan deformálódott testben tárolt energia, például egy megnyújtott vagy összenyomott rugóban. A rugalmas potenciális energia (E\_\{rug\}) egy ideális rugó esetében a következőképpen fejezhető ki (Hooke törvényéből származtatva):
\\displaystyle E\_\{rug\} \= \\frac\{1\}\{2\}kx^2
ahol k a rugóállandó (amely a rugó merevségét jellemzi), és x a rugó egyensúlyi helyzetétől való elmozdulása (megnyúlása vagy összenyomódása). A rugalmas potenciális energia is skaláris mennyiség.
Példák a Rugalmas Potenciális Energiára
Egy összenyomott rugó rugalmas potenciális energiával rendelkezik, amely felszabadulhat, ha a rugó kinyílik, például egy játékpisztolyban, amely egy golyót lő ki. Egy megfeszített íj húrjában is rugalmas potenciális energia tárolódik, amely a nyíl kilövéséhez szükséges kinetikus energiává alakul át.
A Mechanikai Energia Megmaradásának Törvénye
A mechanikai energia megmaradásának törvénye az egyik legalapvetőbb elv a fizikában. Kimondja, hogy egy izolált rendszerben, ahol csak konzervatív erők (mint a gravitáció és a rugalmas erő) hatnak, a rendszer teljes mechanikai energiája (a kinetikus és a potenciális energia összege) állandó marad az időben. Matematikailag ezt így fejezhetjük ki:
\\displaystyle E\_\{mechanikai\} \= E\_k \+ E\_p \= állandó
Ez azt jelenti, hogy az energia nem vész el és nem keletkezik, csak átalakulhat egyik formából a másikba. Például, amikor egy test leesik, a gravitációs potenciális energiája kinetikus energiává alakul át, de a kettő összege állandó (ha elhanyagoljuk a légellenállást).
Konzervatív és Nemkonzervatív Erők
A mechanikai energia megmaradásának törvénye csak akkor érvényes, ha a rendszerben ható erők konzervatívak. Egy erő akkor konzervatív, ha az általa végzett munka független az úttól, csak a kezdő- és végponttól függ. A gravitációs erő és a rugalmas erő példák konzervatív erőkre. Ezzel szemben a nemkonzervatív erők, mint a súrlódás vagy a légellenállás, olyan munkát végeznek, amely függ az úttól, és az általuk végzett munka nem téríthető vissza teljes mértékben más energiaformává (általában hővé alakul). Ha nemkonzervatív erők is jelen vannak, a rendszer teljes mechanikai energiája nem marad állandó, hanem csökkenhet.
Példa a Mechanikai Energia Megmaradására: A Lengőinga
Egy klasszikus példa a mechanikai energia megmaradására a lengőinga. Amikor az inga a legmagasabb pontján van, a sebessége nulla, így a kinetikus energiája is nulla, de a gravitációs potenciális energiája maximális. Ahogy az inga lefelé lendül, a potenciális energia kinetikus energiává alakul át, és a legalacsonyabb ponton a kinetikus energia maximális, míg a potenciális energia minimális (a választott referencia szinttől függően). Ha nem lenne légellenállás és súrlódás a felfüggesztési pontban, az inga örökké lengene, folyamatosan átalakítva a potenciális és kinetikus energiát egymásba, miközben a teljes mechanikai energia állandó maradna.
A Mechanikai Energia Átalakulásai
A mechanikai energia gyakran alakul át más energiaformákká és fordítva. Ahogy fentebb említettük, a potenciális energia kinetikus energiává alakulhat (például egy leeső tárgy esetében), és a kinetikus energia potenciális energiává (például egy felfelé dobott labda esetében, amely lelassul a legmagasabb pontján). Emellett a mechanikai energia átalakulhat hővé (például súrlódás következtében), hanggá (például egy ütközéskor) vagy akár elektromos energiává (például egy generátorban).
Példák a Mechanikai Energia Átalakulására
- Egy autó fékezésekor a mozgási energia (kinetikus energia) a fékekben hővé alakul át a súrlódás miatt.
- Egy vízerőműben a víz gravitációs potenciális energiája először a víz mozgási energiájává alakul át, majd a turbinák forgatásával mechanikai munkává, végül pedig egy generátor segítségével elektromos energiává.
- Amikor egy kalapáccsal egy szögbe ütünk, a kalapács mozgási energiája részben a szög mozgási energiájává és a fa deformálásához szükséges munkává alakul, emellett hő és hang is keletkezik.
- Egy trambulinon ugráló ember folyamatosan alakítja át a gravitációs potenciális energiát rugalmas potenciális energiává (a trambulin rugóiban vagy anyagában) és kinetikus energiává.


A Munka és a Mechanikai Energia Kapcsolata
A munka szorosan kapcsolódik a mechanikai energiához. A munka egy erő által végzett energiaátadás, amikor az erő elmozdít egy testet. Ha egy erő munkát végez egy testen, az megváltoztathatja a test mechanikai energiáját. A munka-energia tétel kimondja, hogy egy testre ható összes erő által végzett nettó munka egyenlő a test kinetikus energiájának megváltozásával:
\\displaystyle W\_\{nettó\} \= \\Delta E\_k \= E\_\{k,végső\} \- E\_\{k,kezdeti\}
Ha csak konzervatív erők végeznek munkát, akkor a teljes mechanikai energia megmarad, ami azt jelenti, hogy a kinetikus energia megváltozása egyenlő a potenciális energia negatív megváltozásával:
\\displaystyle \\Delta E\_k \= \-\\Delta E\_p
vagyis
\\displaystyle \\Delta \(E\_k \+ E\_p\) \= \\Delta E\_\{mechanikai\} \= 0
A Munka Számítása
A munka (W) egy állandó \\mathbf\{F\} erő által végzett munka, amely egy testet \\mathbf\{d\} vektorral elmozdít, a következőképpen számítható ki a skaláris szorzat segítségével:
\\displaystyle W \= \\mathbf\{F\} \\cdot \\mathbf\{d\} \= \|\\mathbf\{F\}\| \|\\mathbf\{d\}\| \\cos \\theta
ahol \|\\mathbf\{F\}\| az erő nagysága, \|\\mathbf\{d\}\| az elmozdulás nagysága, és \\theta az erő és az elmozdulás közötti szög. A munka mértékegysége a joule (J), amely megegyezik egy newton méterrel (N·m).
A Mechanikai Energia Gyakorlati Alkalmazásai
A mechanikai energia elvének megértése és alkalmazása számos technológiai és mérnöki területen elengedhetetlen. Néhány példa:
Energiatermelés
Sok energiatermelési módszer a mechanikai energia átalakításán alapul. A vízerőművek a víz gravitációs potenciális energiáját alakítják át először kinetikus energiává, majd mechanikai munkává a turbinák forgatásával, végül elektromos energiává a generátorokban. A szélenergia a szél kinetikus energiáját használja fel szélturbinák forgatására, ami mechanikai munkát végez, amelyet aztán elektromos árammá alakítanak. A hőerőművekben a hőenergia gőzt termel, amely turbinákat forgatva mechanikai energiát hoz létre, amit aztán elektromos árammá alakítanak.
Közlekedés
A közlekedési eszközök nagymértékben a mechanikai energiára támaszkodnak. A gépjárművek belső égésű motorjai vagy elektromos motorjai mechanikai munkát végeznek a kerekek forgatásához, ami mozgást eredményez. A repülőgépek hajtóművei tolóerőt generálnak, ami a repülőgép kinetikus energiájának növekedéséhez vezet. A vonatok elektromos vagy dízelmotorjai szintén mechanikai energiát használnak a mozgáshoz.
Gyártás és Ipari Folyamatok
A gyártásban és az ipari folyamatokban a mechanikai energia kulcsfontosságú a gépek működtetéséhez. Szerszámgépek, robotok és futószalagok mind mechanikai energiát használnak a feladatok elvégzéséhez. A hidraulikus és pneumatikus rendszerek folyadékok vagy gázok nyomását használják fel mechanikai munka végzésére.
Sport és Szórakozás
A mechanikai energia számos sportban és szórakozási formában is szerepet játszik. Egy labda eldobása vagy egy íjból kilőtt nyíl a testnek adott kinetikus energián alapul. A hullámvasutak a gravitációs potenciális energia és a kinetikus energia folyamatos átalakulásán alapulnak, izgalmas élményt nyújtva.
Összefoglalás
A mechanikai energia a mozgással és a helyzettel kapcsolatos energia, amely két fő formában létezik: kinetikus energia (a mozgás energiája) és potenciális energia (a helyzet vagy konfiguráció energiája). A mechanikai energia megmaradásának törvénye szerint egy izolált rendszer teljes mechanikai energiája állandó marad, ha csak konzervatív erők hatnak. A mechanikai energia folyamatosan átalakulhat más energiaformákká és fordítva, és szorosan kapcsolódik a munkához. A mechanikai energia elvének megértése elengedhetetlen a fizika, a mérnöki tudományok és számos gyakorlati alkalmazás szempontjából, az energiatermeléstől a közlekedésen át a gyártásig és a szórakozásig.