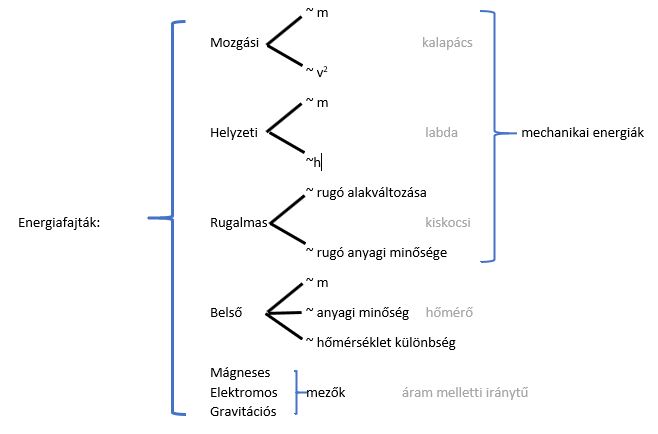
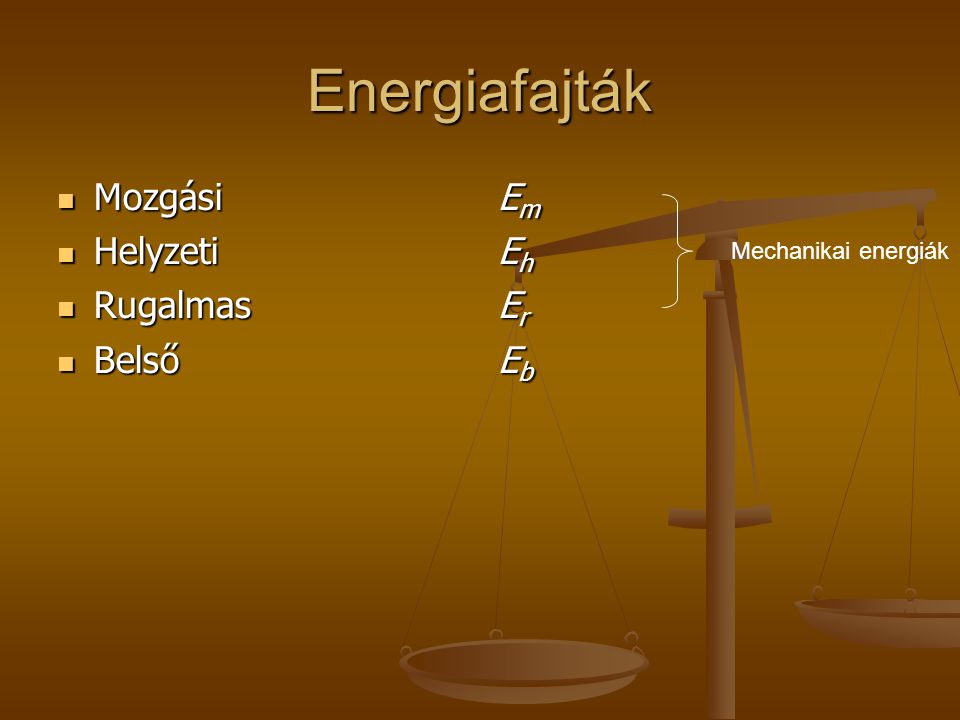
Mechanikai Energiafajtak
A Mechanikai Energia Fajtái: Átfogó Kézikönyv
A mechanikai energia a fizika egyik alapvető fogalma, amely egy test vagy rendszer mozgásával és helyzetével kapcsolatos energiát írja le. Ez az energiaforma kulcsfontosságú a makroszkopikus világ jelenségeinek megértéséhez, a mindennapi tapasztalatainktól kezdve a komplex mérnöki alkalmazásokig. Ebben a részletes útmutatóban feltárjuk a mechanikai energia különböző fajtáit, azok jellemzőit, megjelenési formáit és a velük kapcsolatos alapvető fizikai törvényeket.
A Mechanikai Energia Alapjai
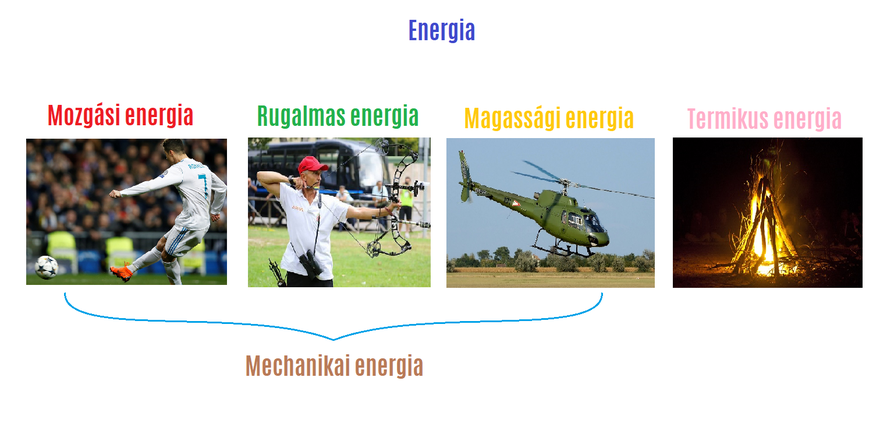
A mechanikai energia fogalma szorosan kapcsolódik a munkavégzés képességéhez. Ha egy erő egy testet elmozdít, munkát végez rajta, és ez a munka megváltoztathatja a test mechanikai energiáját. A mechanikai energia két fő összetevőre bontható: a kinetikus energiára és a potenciális energiára. Ezek az energiafajták együttesen határozzák meg egy rendszer teljes mechanikai energiáját.
Kinetikus Energia: A Mozgás Energiája
A kinetikus energia egy test mozgásából származó energia. Minden olyan objektum, amely mozog, rendelkezik kinetikus energiával. Ennek az energiának a nagysága függ a test tömegétől és sebességétől. Minél nagyobb a test tömege vagy sebessége, annál nagyobb a kinetikus energiája. A kinetikus energia képlete a következő:
\\mathbf\{E\_k \= \\frac\{1\}\{2\}mv^2\}
ahol \(E_k\) a kinetikus energia, \(m\) a test tömege, és \(v\) a test sebessége.
Példák a Kinetikus Energiára
- Egy száguldó autó: Minél gyorsabban halad az autó, annál nagyobb a kinetikus energiája. Egy nehezebb autó azonos sebességnél szintén nagyobb kinetikus energiával rendelkezik.
- Egy repülő labda: A labda mozgása során kinetikus energiával rendelkezik. A dobás erőssége és a labda tömege befolyásolja ezt az energiát.
- Egy forgó kerék: A forgó kerék részei folyamatos mozgásban vannak, így a kerék rendelkezik kinetikus energiával.
A kinetikus energia nem csak a lineáris mozgáshoz kapcsolódik, hanem a forgó mozgáshoz is. A forgó testek forgási kinetikus energiával rendelkeznek, amely a test tehetetlenségi nyomatékától és szögsebességétől függ.
\\mathbf\{E\_\{rot\} \= \\frac\{1\}\{2\}I\\omega^2\}
ahol \(E_{rot}\) a forgási kinetikus energia, \(I\) a tehetetlenségi nyomaték, és \(\omega\) a szögsebesség.
Potenciális Energia: A Helyzetből Adódó Energia
A potenciális energia egy test helyzetéből vagy konfigurációjából származó tárolt energia. Ez az energia akkor szabadulhat fel, ha a test megváltoztatja a helyzetét vagy konfigurációját. A mechanikában két fő típusa van a potenciális energiának: a gravitációs potenciális energia és a rugalmas potenciális energia.

Gravitációs Potenciális Energia
A gravitációs potenciális energia egy testnek a gravitációs mezőben elfoglalt helyzetéből adódik. A Föld felszínén egy \(h\) magasságban lévő \(m\) tömegű test gravitációs potenciális energiája a következőképpen számítható ki:
\\mathbf\{E\_p \= mgh\}
ahol \(E_p\) a gravitációs potenciális energia, \(m\) a test tömege, \(g\) a gravitációs gyorsulás (a Földön körülbelül \(9.81 \, m/s^2\)), és \(h\) a test magassága egy referencia szinthez képest.
Példák a Gravitációs Potenciális Energiára
- Egy hegy tetején lévő kő: A kőnek magasságából adódóan gravitációs potenciális energiája van. Ha a kő leesik, ez az energia kinetikus energiává alakul át.
- Egy víztározóban lévő víz: A magasabban lévő víz gravitációs potenciális energiával rendelkezik, amelyet a vízerőművek elektromos áram előállítására használnak fel.
- Egy fán lévő alma: Az almának a földfelszínhez viszonyított magassága miatt gravitációs potenciális energiája van. Amikor leesik, ez az energia mozgási energiává alakul.
Rugalmas Potenciális Energia
A rugalmas potenciális energia egy rugalmasan deformálható test (például egy rugó vagy egy gumiszalag) megfeszítéséből vagy összenyomásából származik. A rugalmas erővel szemben végzett munka tárolódik ebben az energiaformában. Egy ideális rugó rugalmas potenciális energiája a következőképpen adható meg:
\\mathbf\{E\_\{elas\} \= \\frac\{1\}\{2\}kx^2\}
ahol \(E_{elas}\) a rugalmas potenciális energia, \(k\) a rugóállandó (amely a rugó merevségét jellemzi), és \(x\) a rugó egyensúlyi helyzetétől való elmozdulása.
Példák a Rugalmas Potenciális Energiára
- Egy megfeszített rugó: Amikor egy rugót megfeszítünk vagy összenyomunk, rugalmas potenciális energiát tárol. Ez az energia szabadul fel, amikor a rugó visszatér eredeti alakjába.
- Egy kilőtt nyíl: A megfeszített íj húrjában tárolt rugalmas potenciális energia alakul át a nyíl kinetikus energiájává.
- Egy trambulin: Amikor valaki ráugrik a trambulinra, a rugók megfeszülnek, rugalmas potenciális energiát tárolva, amely aztán visszalökő erőt fejt ki.
A Mechanikai Energia Megmaradása
Az egyik legfontosabb elv a fizikában az energia megmaradásának törvénye, amely kimondja, hogy egy zárt rendszer teljes energiája állandó marad, feltéve, hogy nincsenek nem-konzervatív erők (például súrlódás vagy légellenállás) munkája. A mechanikai energia esetében ez azt jelenti, hogy egy olyan rendszerben, ahol csak konzervatív erők hatnak, a kinetikus energia és a potenciális energia összege állandó marad:
\\mathbf\{E\_\{mech\} \= E\_k \+ E\_p \= állandó\}
Példák az Energia Megmaradására
- Egy ingamozgás: Amikor az inga a legmagasabb pontján van, a potenciális energiája maximális, a kinetikus energiája pedig nulla. Ahogy az inga lefelé mozog, a potenciális energia kinetikus energiává alakul át. A legalacsonyabb ponton a kinetikus energia maximális, a potenciális energia pedig minimális. Ideális esetben a teljes mechanikai energia (a kinetikus és a potenciális energia összege) állandó marad.
- Egy leeső tárgy: Amikor egy tárgyat elejtünk, a kezdeti magasságban gravitációs potenciális energiával rendelkezik. Ahogy esik, ez az energia fokozatosan kinetikus energiává alakul át. Közvetlenül a földbe csapódás előtt a kinetikus energia maximális, a potenciális energia pedig minimális (a referencia szinttől függően).
Nem-Konzervatív Erők és a Mechanikai Energia Disszipációja
A valóságban gyakran vannak jelen nem-konzervatív erők, mint például a súrlódás és a légellenállás. Ezek az erők munkát végeznek a rendszeren, és ez a munka nem tárolódik potenciális energiaként, hanem általában hővé alakul. Ebben az esetben a teljes mechanikai energia nem marad meg, hanem csökken. Ezt az energiacsökkenést disszipációnak nevezzük.
Példák a Mechanikai Energia Disszipációjára
- Egy csúszó tárgy: Amikor egy tárgy egy felületen csúszik, a súrlódási erő munkát végez, és a mechanikai energia egy része hővé alakul, felmelegítve a tárgyat és a felületet. Ennek eredményeként a tárgy mozgása lelassul és végül megáll.
- Egy fékező autó: Az autó fékezése során a kinetikus energia a fékekben súrlódási hővé alakul, ami lelassítja az autót.
A Mechanikai Energia Átalakulásai
A mechanikai energia különböző formái egymásba alakulhatnak. Láttuk már a potenciális energia kinetikus energiává való átalakulását egy leeső tárgy vagy egy inga esetében, és fordítva, a kinetikus energia potenciális energiává alakulását egy felfelé dobott labda esetében, amely eléri a legmagasabb pontját.
További Példák az Energia Átalakulásaira
- Egy vízerőmű: A víztározóban lévő víz gravitációs potenciális energiája a turbinákon átfolyva kinetikus energiává alakul, amely aztán elektromos generátort hajt meg.
- Egy autó motorja: A benzin kémiai energiája először hővé, majd a mozgó alkatrészek révén mechanikai energiává alakul.
- Egy szélmalom: A szél kinetikus energiája a lapátokat forgatva mechanikai energiává alakul, amelyet aztán különböző célokra lehet felhasználni.
A Mechanikai Energia Jelentősége és Alkalmazásai
A mechanikai energia megértése és hasznosítása alapvető fontosságú számos tudományterületen és technológiai alkalmazásban.
Mérnöki Alkalmazások
- Gépészet: A gépek tervezése és működtetése a mechanikai energia átalakításán és továbbításán alapul.
- Építőmérnökség: Az épületek és hidak stabilitásának és a terhelések elviselésének megértéséhez elengedhetetlen a mechanikai erők és energiák ismerete.
- Repüléstechnika: A repülőgépek mozgása és a felhajtóerő létrehozása a mechanikai elveken alapul.

Mindennapi Élet
- A közlekedési eszközök (autók, vonatok, kerékpárok) mechanikai energiát használnak a mozgáshoz.
- A háztartási gépek (mosógép, turmixgép) működéséhez mechanikai energiára van szükség.
- A sporteszközök (labdák, ütők) használata során a mechanikai energia átalakulásai figyelhetők meg.
Összefoglalás
A mechanikai energia a mozgással és a helyzettel kapcsolatos energia. Két fő fajtája van: a kinetikus energia (a mozgás energiája) és a potenciális energia (a helyzetből adódó tárolt energia, amely lehet gravitációs vagy rugalmas). Egy zárt rendszerben, ahol csak konzervatív erők hatnak, a mechanikai energia megmarad. A valóságban azonban nem-konzervatív erők is jelen lehetnek, amelyek a mechanikai energia disszipációjához vezetnek. A mechanikai energia megértése kulcsfontosságú a természeti jelenségek és a technológiai alkalmazások széles körének megértéséhez.
További Tudnivalók a Mechanikai Energiáról
A mechanikai energia fogalmának mélyebb megértéséhez érdemes megvizsgálni a munka-energia tételt is, amely összekapcsolja a munkát és az energiaváltozást. A tétel kimondja, hogy egy testre ható összes erő által végzett munka egyenlő a test kinetikus energiájának megváltozásával:
\\mathbf\{W\_\{net\} \= \\Delta E\_k \= E\_\{k,f\} \- E\_\{k,i\}\}
ahol \(W_{net}\) a nettó munka, \(\Delta E_k\) a kinetikus energia változása, \(E_{k,f}\) a végső kinetikus energia, és \(E_{k,i}\) a kezdeti kinetikus energia.
A Konzervatív Erők és a Potenciális Energia Kapcsolata
A potenciális energia fogalma szorosan kapcsolódik a konzervatív erőkkel. Egy erő akkor konzervatív, ha az általa végzett munka egy zárt úton nulla, vagy ha a két pont között végzett munka független az útvonaltól. A gravitációs erő és a rugalmas erő tipikus példái a konzervatív erőknek. A potenciális energia definíció szerint a konzervatív erő által végzett munka negatívja:
\\mathbf\{\\Delta U \= \-W\_c\}
ahol \(\Delta U\) a potenciális energia változása, és \(W_c\) a konzervatív erő által végzett munka.
A Mechanikai Energia Mérésének Egységei
A mechanikai energiát (mind a kinetikus, mind a potenciális formában) a Nemzetközi Mértékegységrendszerben (SI) joule-ban (J) mérik. Egy joule egyenlő egy newton méterrel (N·m), vagy alapegységekben \(kg \cdot m^2/s^2\).
Komplexebb Rendszerek Mechanikai Energiája
Több testből álló rendszerek esetében a teljes mechanikai energia az egyes testek kinetikus és potenciális energiáinak összege. Például egy bolygórendszerben a bolygók kinetikus energiájának és a bolygók közötti gravitációs potenciális energiának az összege adja a rendszer teljes mechanikai energiáját.
Molekuláris szintű Mechanikai Energia
Bár a mechanikai energia fogalmát leggyakrabban makroszkopikus objektum