Magneses Indukciovektor

A mágneses indukcióvektor: Átfogó tanulmány a mágneses tér alapvető fogalmáról

A mágneses indukcióvektor, amelyet gyakran \\mathbf\{B\}-vel jelölünk, a mágneses tér egyik legfontosabb és legmeghatározóbb mennyisége. Ez a vektormennyiség nem csupán a mágneses tér erősségét írja le egy adott pontban, hanem annak irányát is. A mágneses indukcióvektor megértése elengedhetetlen az elektromágnesség jelenségeinek mélyreható tanulmányozásához, kezdve az egyszerű mágneses erőhatásoktól egészen a komplex elektromágneses hullámokig és a modern technológiai alkalmazásokig.

A mágneses indukcióvektor definíciója és alapjai

A mágneses indukcióvektor formális definíciója a Lorentz-erőn keresztül történik. Ha egy q töltésű részecske \\mathbf\{v\} sebességgel mozog egy olyan térben, ahol mind elektromos (\\mathbf\{E\}) és mágneses (\\mathbf\{B\}) tér is jelen van, akkor a részecskére ható teljes erő, a Lorentz-erő a következőképpen adható meg:

$$ \mathbf{F} = q(\mathbf{E} + \mathbf{v} \times \mathbf{B}) $$

Ebben az egyenletben a \\mathbf\{v\} \\times \\mathbf\{B\} tag képviseli a mágneses erő komponensét. Látható, hogy a mágneses erő függ a töltés sebességétől és a mágneses indukcióvektor kereszttermékétől. Ez azt jelenti, hogy a mágneses erő mindig merőleges a töltés sebességére és a mágneses indukcióvektorra is.

A mágneses indukcióvektor mértékegysége

A mágneses indukcióvektor SI-mértékegysége a tesla (T). Egy tesla az a mágneses indukció, amely egy 1 coulomb töltésű, 1 méter per szekundum sebességgel mozgó részecskére 1 newton nagyságú, a sebességére és a mágneses térre is merőleges erőt fejt ki. Másik gyakran használt mértékegység a gauss (G), ahol 1 T = 10 000 G.

A mágneses indukcióvektor tulajdonságai

A mágneses indukcióvektornak számos fontos tulajdonsága van, amelyek elengedhetetlenek a mágneses jelenségek megértéséhez:

• Ez egy vektormennyiség, ami azt jelenti, hogy mind nagysága, mind iránya van.
• A mágneses erő, amelyet egy mozgó töltésre kifejt, arányos a mágneses indukcióvektor nagyságával.

• A mágneses erő iránya merőleges mind a töltés sebességére, mind a mágneses indukcióvektorra.
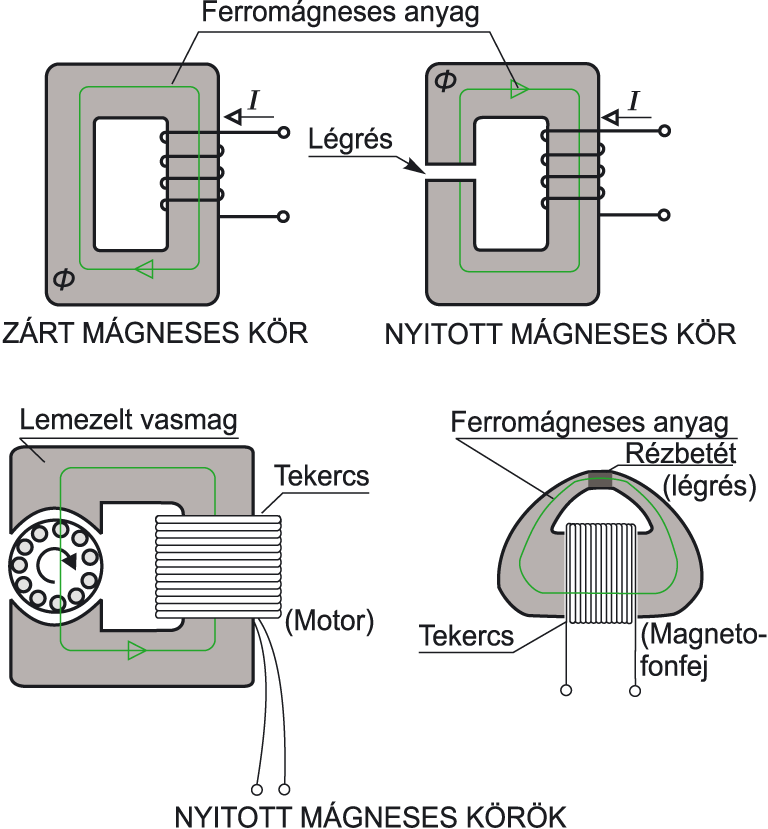
• A mágneses indukcióvonalak zárt görbéket alkotnak; nincsenek mágneses monopólusok. Ez a tény a Maxwell-egyenletek egyik alapvető megállapítása.
• A mágneses indukcióvektor szorosan összefügg a mágneses fluxussal. A mágneses fluxus (\\Phi\_B) egy adott felületen áthaladó mágneses indukcióvonalak számának mértéke, amelyet a következőképpen definiálunk:
  

  $$ \Phi_B = \int \mathbf{B} \cdot d\mathbf{A} $$

  ahol d\\mathbf\{A\} a felület infinitezimális vektoros eleme.

A mágneses indukcióvonalak

A mágneses indukcióvonalak képzeletbeli vonalak, amelyek a mágneses tér irányát szemléltetik. Ezek a vonalak a mágneses indukcióvektor irányába mutatnak minden pontban. Fontos megjegyezni, hogy a mágneses indukcióvonalak mindig zárt hurkokat alkotnak, ami a mágneses monopólusok hiányának következménye. A vonalak sűrűsége egy adott területen arányos a mágneses indukcióvektor nagyságával azon a területen.

A mágneses indukcióvektor forrásai

A mágneses indukcióvektort mozgó elektromos töltések és mágneses anyagok hozhatják létre.

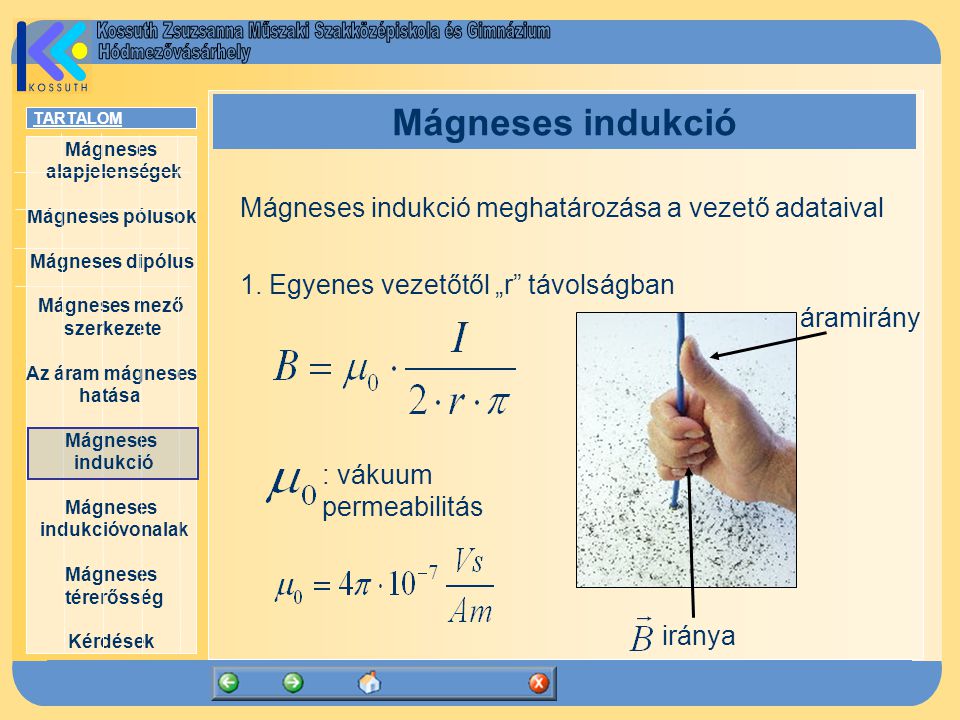
Áramjárta vezetők

Egy áramjárta vezető körül mágneses tér alakul ki. Az áram által létrehozott mágneses indukcióvektor nagysága és iránya az áram erősségétől, a vezető geometriájától és a megfigyelési pont helyzetétől függ. A Biot-Savart törvény adja meg az infinitezimális áramszegmens által létrehozott mágneses indukcióvektort:

$$ d\mathbf{B} = \frac{\mu_0}{4\pi} \frac{I d\mathbf{l} \times \mathbf{r}}{r^3} $$

ahol I az áram erőssége, d\\mathbf\{l\} az áramszegmens vektoros hossza, \\mathbf\{r\} a helyvektor az áramszegmenstől a megfigyelési pontig, r a \\mathbf\{r\} vektor nagysága, és \\mu\_0 a vákuum permeabilitása (4\\pi \\times 10^\{\-7\} \\, \\text\{T m/A\}).

Példa: Egyenes áramjárta vezető mágneses indukcióvektora

Egy hosszú, egyenes áramjárta vezető körül a mágneses indukcióvonalak koncentrikus körök, amelyek középpontja a vezető tengelyében van, és a síkjuk merőleges a vezetőre. A mágneses indukcióvektor nagysága egy r távolságra a vezetőtől a következőképpen adható meg:

$$ B = \frac{\mu_0 I}{2\pi r} $$

Az irányát a jobbkéz-szabály adja meg: ha a jobb hüvelykujjunk az áram irányába mutat, akkor a begörbülő ujjaink a mágneses indukcióvektor irányát jelzik.

Mágneses anyagok

A mágneses anyagok, mint például a ferromágneses anyagok (vas, nikkel, kobalt), saját belső mágneses tereket hozhatnak létre atomi szinten lévő elektronok spinjének és pályamozgásának köszönhetően. Ezek az atomi dipólusmomentumok rendeződhetnek külső mágneses tér hatására, vagy akár spontán módon is, létrehozva egy makroszkopikus mágneses teret. A mágneses indukcióvektor egy mágneses anyagban függ a külső mágneses tértől és az anyag magnetizációjától (\\mathbf\{M\}):

$$ \mathbf{B} = \mu_0 (\mathbf{H} + \mathbf{M}) $$

ahol \\mathbf\{H\} a mágneses térerősség.

A mágneses indukcióvektor mérése

A mágneses indukcióvektor mérésére különböző módszereket alkalmaznak, attól függően, hogy milyen erősségű és jellegű a mérendő mágneses tér.

Hall-effektus szenzorok

A Hall-effektus egy olyan jelenség, amely során egy áramjárta vezetőben vagy félvezetőben, a vezetőre merőleges mágneses tér hatására, a töltéshordozók elhajlanak, és a vezető keresztirányában feszültségkülönbség (Hall-feszültség) jön létre. A Hall-feszültség nagysága arányos a mágneses indukcióvektor erősségével, így a Hall-effektus szenzorok széles körben használatosak mágneses tér mérésére.

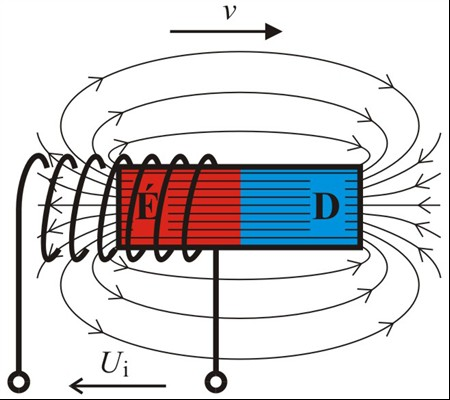
Tekercsek és Faraday törvénye

A Faraday-féle indukciós törvény kimondja, hogy egy zárt vezetőben indukált elektromotoros erő arányos a vezetőt körülvevő mágneses fluxus időbeli változásának sebességével:

$$ \mathcal{E} = -\frac{d\Phi_B}{dt} $$

Ezt a törvényt felhasználva, egy mérőtekercsbe indukált feszültség mérésével következtethetünk a mágneses tér erősségére. Ha a mágneses tér változik, vagy ha a tekercs mozog a mágneses térben, mágneses fluxus változik, ami indukált feszültséget eredményez. A mért feszültségből, a tekercs geometriájának ismeretében, meghatározható a mágneses indukcióvektor.

SQUID-ok (szupravezető kvantum interferencia eszközök)

A SQUID-ok rendkívül érzékeny magnetométerek, amelyek a szupravezetés kvantummechanikai tulajdonságait használják ki a nagyon gyenge mágneses terek mérésére. Alkalmazásuk kiterjed a geofizikától az orvosi diagnosztikáig (pl. magnetoenkefalográfia).

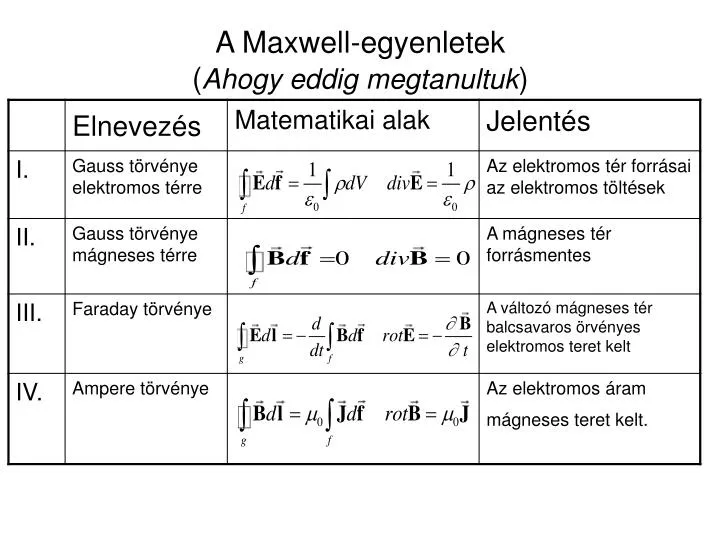
A mágneses indukcióvektor és a Maxwell-egyenletek

A mágneses indukcióvektor központi szerepet játszik a Maxwell-egyenletekben, amelyek az elektromágnesség alapvető törvényeit foglalják össze:

1. Gauss törvénye az elektromosságról: \\nabla \\cdot \\mathbf\{E\} \= \\frac\{\\rho\}\{\\epsilon\_0\}
2. Gauss törvénye a mágnességről: \\nabla \\cdot \\mathbf\{B\} \= 0 (a mágneses monopólusok hiánya)
3. Faraday indukciós törvénye: \\nabla \\times \\mathbf\{E\} \= \-\\frac\{\\partial \\mathbf\{B\}\}\{\\partial t\}
4. Ampère-Maxwell törvény: \\nabla \\times \\mathbf\{B\} \= \\mu\_0 \\left\( \\mathbf\{J\} \+ \\epsilon\_0 \\frac\{\\partial \\mathbf\{E\}\}\{\\partial t\} \\right\)

A második Maxwell-egyenlet, \\nabla \\cdot \\mathbf\{B\} \= 0, kifejezi azt a tényt, hogy nincsenek mágneses monopólusok, és a mágneses indukcióvonalak mindig zártak. A harmadik egyenlet, a Faraday-törvény, leírja, hogy a változó mágneses tér elektromos teret indukál. A negyedik egyenlet, az Ampère-Maxwell törvény, azt mutatja meg, hogy az elektromos áram és a változó elektromos tér mágneses teret hoz létre.

A mágneses indukcióvektor gyakorlati alkalmazásai

A mágneses indukcióvektor megértése és mérése számos technológiai alkalmazás alapját képezi:

• Elektromos motorok és generátorok: Ezek az eszközök a mágneses erő elvén működnek, amely egy áramjárta vezetőre hat mágneses térben.
• Transzformátorok: A Faraday-féle indukció elvén működnek, ahol egy változó mágneses fluxus elektromos feszültséget indukál egy másik tekercsben.
• Adatrögzítés: A merevlemezek és más mágneses adathordozók a mágneses domének irányának megváltoztatásával tárolják az információt.
• Orvosi képalkotás (MRI): A mágneses rezonancia képalkotás erős mágneses tereket és rádióhullámokat használ a test belső szerkezetének részletes képeinek létrehozására.
• Navigáció: A Föld mágneses terét iránytűk és más navigációs eszközök használják az irány meghatározására.
• Tudományos kutatás: A mágneses terek tanulmányozása elengedhetetlen a plazmafizikában, az asztrofizikában és az anyagtudományban.

A mágneses indukcióvektor szerepe az MRI-ben

A mágneses rezonancia képalkotás (MRI) egy orvosi képalkotó eljárás, amely erős mágneses tereket használ a test belsejének részletes képeinek létrehozására. A folyamat során a páciens egy erős, statikus mágneses térbe kerül, amelynek mágneses indukcióvektora tipikusan 1,5 és 7 tesla között van. Ez a mágneses tér hatására a testben lévő vízmolekulák hidrogénatomjainak protonjai (amelyeknek saját mágneses momentumuk van) a mágneses tér irányába rendeződnek. Ezután rádiófrekvenciás impulzusokat bocsátanak ki, amelyek rezonanciába hozzák a protonokat. Amikor az impulzusok megszűnnek, a protonok visszatérnek eredeti állapotukba, miközben rádióhullámokat bocsátanak ki. Ezeket a hullámokat érzékelik a MRI-szkenner detektorai, és a jelekből számítógépes algoritmusok segítségével részletes képeket alkotnak a test belső szerkezetéről. A mágneses indukcióvektor erőssége és homogenitása kulcsfontosságú a kiváló minőségű MRI-képek eléréséhez.

A mágneses indukcióvektor a geofizikában

A Földnek is van saját mágneses tere, amelyet elsősorban a Föld külső magjában lévő olvadt vas áramlásai generálnak (geodinamo). A Föld mágneses indukcióvektora a felszínen körülbelül 25 és 65 mikrotesla között változik. Ez a mágneses tér fontos szerepet játszik a navigációban (iránytűk), védelmet nyújt a káros kozmikus sugárzás és a napszél ellen (magnetoszféra), és információkat hordoz a Föld múltbeli mágneses teréről (paleomágnesség). A geofizikusok a mágneses indukcióvektor mérésével és elemzésével tanulmányozzák a Föld belső szerkezetét, a kőzetek mágneses tulajdonságait és a mágneses tér időbeli változásait.

Összefoglalás

Magneses Indukcio Keplet

A Mágneses Indukció Képlete: Mélyreható Elemzés és Alkalmazások

A Mágneses Indukció Alapjai

A mágneses indukció egy alapvető jelenség az elektromágnesség területén, amely leírja, hogyan hoz létre egy változó mágneses tér elektromos teret. Ez a kölcsönhatás képezi számos modern technológia működésének alapját, a generátoroktól a transzformátorokig. Ahhoz, hogy teljes mértékben megértsük a mágneses indukció képletét, először is tisztáznunk kell a kapcsolódó alapfogalmakat, mint például a mágneses fluxus és Faraday törvénye.

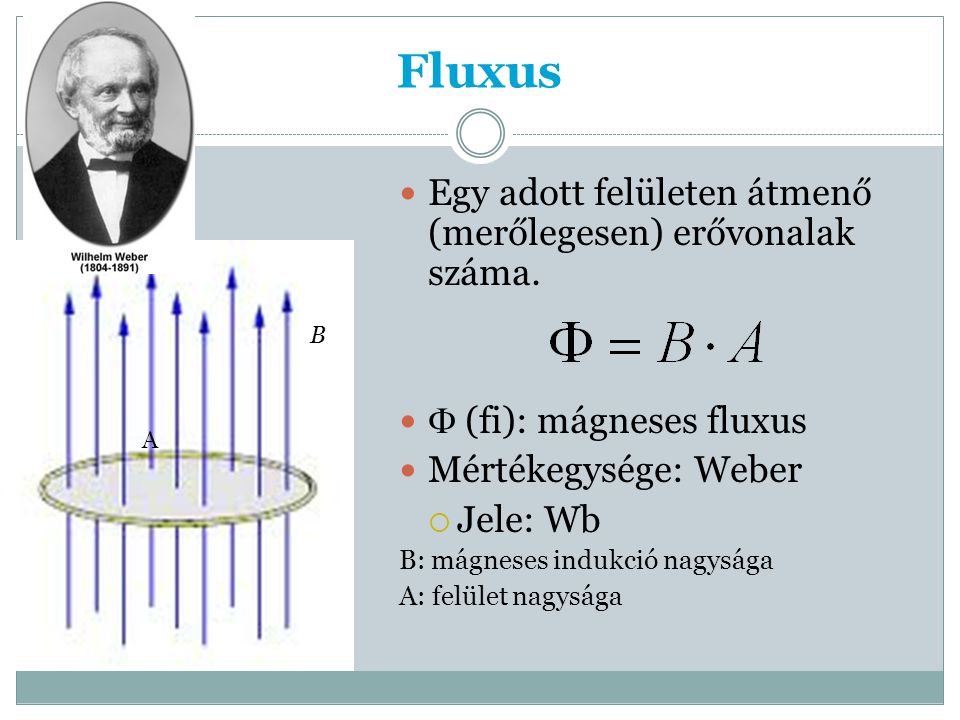
A Mágneses Fluxus Fogalma

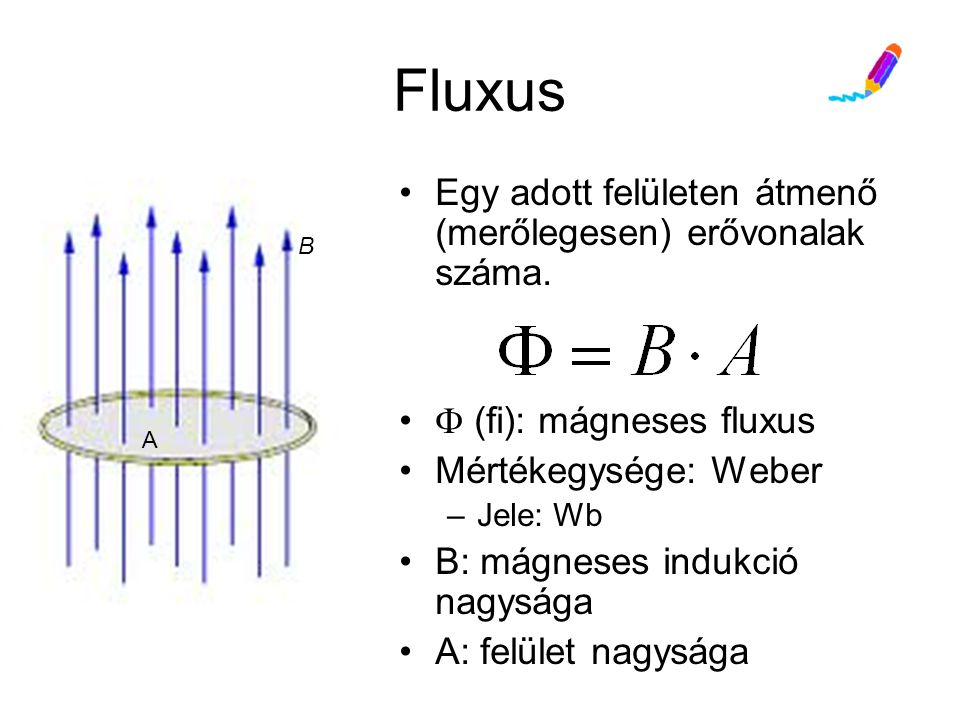
A mágneses fluxus (\\Phi\_B) egy adott felületen áthaladó mágneses tér mennyiségének mértéke. Képzeljünk el egy mágneses teret, amelyet mágneses térvonalakkal ábrázolunk. A mágneses fluxus arányos azzal a vonalszámmal, amely egy adott felületet áthalad. Matematikailag a mágneses fluxust a következőképpen definiáljuk:

\\Phi\_B \= \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}

Ahol \\mathbf\{B\} a mágneses indukció vektor (más néven mágneses tér sűrűség), és d\\mathbf\{A\} a felület egy infiniteszimális elemének vektoros területe, amelynek iránya merőleges a felületre. Ha a mágneses tér homogén a felületen, és a mágneses tér vektor párhuzamos a felület normálisával, akkor a képlet egyszerűsödik:

\\Phi\_B \= BA \\cos\{\\theta\}

Ahol B a mágneses tér erőssége, A a felület területe, és \\theta a mágneses tér vektor és a felület normálisának szöge. A mágneses fluxus mértékegysége a Weber (Wb), ahol 1 Wb = 1 Tm$^2$ (Tesla-négyzetméter).

Faraday Indukciós Törvénye

Michael Faraday kísérletei során fedezte fel az elektromágneses indukció alapvető törvényét. Faraday törvénye kimondja, hogy egy zárt áramkörben indukált elektromotoros erő (EMF, \\mathcal\{E\}) egyenlő a mágneses fluxus időbeli változásának negatívjával az áramkörön keresztül:

\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}

Ez a képlet a mágneses indukció képletének központi eleme. A negatív előjel Lenz törvényét tükrözi, amely szerint az indukált áram iránya olyan, hogy mágneses terével akadályozza a fluxus változását, amely létrehozta őt.

Az Indukált Elektromotoros Erő Részletesebben

Az indukált elektromotoros erő (EMF) valójában egy potenciálkülönbség, amely egy vezetőben vagy áramkörben jön létre a változó mágneses fluxus hatására. Ez az EMF képes áramot hajtani, ha az áramkör zárt. A Faraday-féle indukciós törvény kvantitatív kapcsolatot teremt a változó mágneses fluxus és az indukált EMF között.

Lenz Törvényének Szerepe

Mint említettük, a Faraday-féle indukciós törvényben szereplő negatív előjel a Lenz-törvény következménye. Lenz törvénye elengedhetetlen az indukált áram és az indukált mágneses tér irányának meghatározásához. Egyszerűen fogalmazva, az indukált áram olyan irányú, hogy az általa létrehozott mágneses tér ellentétes a fluxus változásával, amely az indukciót okozta. Ez az elv biztosítja az energiamegmaradást az elektromágneses indukciós folyamatokban.

A Mágneses Indukció Képletének Levezetése Mozgó Vezető Esetén

Tekintsünk egy l hosszúságú vezetőt, amely egy homogén \\mathbf\{B\} mágneses térben v sebességgel mozog, úgy hogy a sebességvektor merőleges a mágneses tér vektorra és a vezetőre is. A vezetőben lévő töltött részecskékre (például elektronokra) ható mágneses erő a Lorentz-erő:

\\mathbf\{F\} \= q\(\\mathbf\{v\} \\times \\mathbf\{B\}\)

Ahol q a töltés. Az elektronokra ható erő iránya a jobbkéz-szabály szerint meghatározható. Ennek az erőnek a hatására a töltések a vezető mentén elmozdulnak, ami egy elektromos teret hoz létre a vezetőben. Amikor a mágneses erő által létrehozott elektromos erő egyensúlyba kerül a töltésekre ható mágneses erővel, egy állandó elektromos tér alakul ki.

Az indukált elektromotoros erő a vezető két vége közötti potenciálkülönbség:

\\mathcal\{E\} \= \\int \(\\mathbf\{v\} \\times \\mathbf\{B\}\) \\cdot d\\mathbf\{l\}

Ha \\mathbf\{v\}, \\mathbf\{B\} és d\\mathbf\{l\} páronként merőlegesek egymásra, akkor ez leegyszerűsödik:

\\mathcal\{E\} \= Blv

Ez a képlet azt mutatja, hogy egy mozgó vezetőben indukált EMF arányos a mágneses tér erősségével, a vezető hosszával és a sebességével.

A Mágneses Indukció Képletének Levezetése Változó Mágneses Tér Esetén

Most vizsgáljuk meg azt az esetet, amikor egy rögzített áramkörben változik a mágneses fluxus. Faraday törvénye közvetlenül megadja az indukált EMF-et:

\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}

Ha a mágneses tér időben változik, de a felület állandó, akkor a fluxus időbeli deriváltja a mágneses tér időbeli deriváltjával függ össze:

\\frac\{d\\Phi\_B\}\{dt\} \= \\frac\{d\}\{dt\} \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\} \= \\int \\frac\{\\partial \\mathbf\{B\}\}\{\\partial t\} \\cdot d\\mathbf\{A\}

Így az indukált EMF:

\\mathcal\{E\} \= \-\\int \\frac\{\\partial \\mathbf\{B\}\}\{\\partial t\} \\cdot d\\mathbf\{A\}

Ez a forma a mágneses indukció képletének egy általánosabb megközelítése, amely a változó mágneses tér hatására létrejövő elektromos teret írja le.

A Mágneses Indukció és az Elektromos Tér kapcsolata: Faraday-Maxwell törvény

A Faraday-féle indukciós törvény a Maxwell-egyenletek egyik alapvető formája, amely összekapcsolja a változó mágneses teret az elektromos térrel. Integrális formában a Faraday-Maxwell törvény így szól:

\\oint \\mathbf\{E\} \\cdot d\\mathbf\{l\} \= \-\\frac\{d\}\{dt\} \\iint\_S \\mathbf\{B\} \\cdot d\\mathbf\{A\} \= \-\\frac\{d\\Phi\_B\}\{dt\}

Ahol a bal oldalon az elektromos tér vonalintegrálja egy zárt görbe mentén, a jobb oldalon pedig a mágneses fluxus időbeli változása a görbe által határolt felületen keresztül látható. Ez az egyenlet azt fejezi ki, hogy egy változó mágneses fluxus elektromos teret indukál.

Differenciális formában a Faraday-Maxwell törvény:

\\nabla \\times \\mathbf\{E\} \= \-\\frac\{\\partial \\mathbf\{B\}\}\{\\partial t\}

Ez a forma lokális kapcsolatot ír le a térben az elektromos tér rotációja és a mágneses tér időbeli változása között.

Az Induktivitás Fogalma

Az induktivitás (L) egy áramkör azon tulajdonsága, amely ellenáll az áram változásának önindukció vagy kölcsönös indukció révén. Ha egy áramkörben áram folyik, mágneses fluxust hoz létre, amely arányos az árammal:

\\Phi\_B \= LI

Ahol I az áram. Ha az áram időben változik, a mágneses fluxus is változik, ami Faraday törvénye szerint elektromotoros erőt indukál az áramkörben:

\\mathcal\{E\} \= \-L \\frac\{dI\}\{dt\}

Ez az önindukció jelensége. Az induktivitás mértékegysége a Henry (H).

Kölcsönös Indukció

A kölcsönös indukció akkor lép fel, ha egy áramkörben változó áram egy másik közeli áramkörben is elektromotoros erőt indukál a két áramkör által megosztott mágneses fluxus változása miatt. Ha az 1. áramkörben I\_1 áram folyik, a 2. áramkörben létrejövő mágneses fluxus \\Phi\_\{21\} \= M\_\{21\}I\_1, ahol M\_\{21\} a 2. áramkör 1. áramkörre vonatkozó kölcsönös induktivitása. A 2. áramkörben indukált EMF:

\\mathcal\{E\}\_2 \= \-\\frac\{d\\Phi\_\{21\}\}\{dt\} \= \-M\_\{21\} \\frac\{dI\_1\}\{dt\}

Hasonlóképpen, az 1. áramkörben az áram változása a 2. áramkörben fluxust hoz létre, \\Phi\_\{12\} \= M\_\{12\}I\_2, és az 1. áramkörben indukált EMF:

\\mathcal\{E\}\_1 \= \-\\frac\{d\\Phi\_\{12\}\}\{dt\} \= \-M\_\{12\} \\frac\{dI\_2\}\{dt\}

M\_\{12\} \= M\_\{21\} \= M, amelyet egyszerűen kölcsönös induktivitásnak nevezünk.

A Mágneses Indukció Alkalmazásai

A mágneses indukció elve számos technológiai alkalmazás alapját képezi:

Elektromos Generátorok

A generátorok mechanikai energiát alakítanak át elektromos energiává a mágneses indukció segítségével. Egy tekercset vagy vezetőt egy mágneses térben forgatnak, ami a mágneses fluxus változását okozza a tekercsen keresztül, indukálva ezzel egy elektromotoros erőt és áramot.

Transzformátorok

A transzformátorok a kölcsönös indukció elvén működnek. Két vagy több tekercsből állnak, amelyek egy közös mágneses magra vannak feltekercselve. Egyik tekercsben (primer tekercs) változó áramot vezetnek, ami változó mágneses fluxust hoz létre a magban. Ez a változó fluxus elektromotoros erőt indukál a másik tekercsben (szekunder tekercs), lehetővé téve a feszültség és az áram átalakítását.

Indukciós Főzés

Az indukciós főzőlapok változó mágneses teret használnak, hogy áramot indukáljanak a főzőedény aljában. Ez az indukált áram (örvényáram) felmelegíti az edényt, így főzve meg az ételt.

Elektromágneses Fékek

Bizonyos járművekben elektromágneses fékeket használnak, amelyek a mágneses indukció elvén működnek. A mozgó kerekekkel együtt forgó féktárcsába mágneses teret hoznak létre, ami örvényáramokat indukál a tárcsában. Ezek az áramok mágneses teret hoznak létre, amely ellentétes az eredetivel, így fékező hatást eredményez.

Vezeték Nélküli Töltés

A vezeték nélküli töltési technológiák, mint például a mobiltelefonok töltése, szintén a mágneses indukciót használják. Egy adótekercsben váltakozó áramot vezetnek, ami változó mágneses teret hoz létre. Ez a tér elektromos áramot indukál a vevőtekercsben, amely a töltendő eszközben található.

Példák a Mágneses Indukció Képletének Alkalmazására

Példa 1: Mozgó vezető

Egy 0.5 m hosszú vezető 2 T erősségű mágneses térben mozog 10 m/s sebességgel, úgy hogy a sebesség merőleges a mágneses térre és a vezetőre. Számítsuk ki az indukált elektromotoros erőt!

Használjuk a \\mathcal\{E\} \= Blv képletet:

\\mathcal\{E\} \= \(2 \\, \\text\{T\}\) \\times \(0\.5 \\, \\text\{m\}\) \\times \(10 \\, \\text\{m/s\}\) \= 10 \\, \\text\{V\}

Tehát az indukált elektromotoros erő 10 V.

Példa 2: Változó mágneses fluxus

Egy 0.1 m

Magneses Fluxus

A Mágneses Fluxus Részletes Tanulmánya

Ebben az átfogó cikkben részletesen feltárjuk a mágneses fluxus fogalmát, jelentőségét a fizika és a mérnöki tudományok területén. Megvizsgáljuk annak alapvető definíciójától kezdve a gyakorlati alkalmazásáig terjedő széles spektrumát. Célunk, hogy egy olyan mélyreható és érthető magyarázatot nyújtsunk, amely mind a diákok, mind a szakemberek számára értékes forrásként szolgál.

A Mágneses Fluxus Alapjai

Mi a Mágneses Fluxus?

A mágneses fluxus (\\Phi\_B) egy adott felületen áthaladó mágneses tér mennyiségének a mérőszáma. Képzeljünk el egy mágneses teret, amelyet vonalak szemléltetnek. A mágneses fluxus arányos azzal a vonalszámmal, amely egy adott felületet áthalad. Pontosabban, a mágneses fluxus a mágneses indukcióvektor (\\mathbf\{B\}) és a felület normálvektorának (\\mathbf\{A\}) skaláris szorzata, integrálva a felületen.

A Mágneses Fluxus Képlete

Matematikailag a mágneses fluxust a következőképpen fejezhetjük ki:

\\Phi\_B \= \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}

ahol:

• \\Phi\_B a mágneses fluxus (Weberben, Wb)
• \\mathbf\{B\} a mágneses indukcióvektor (Tesla, T)
• d\\mathbf\{A\} a felület egy infiniteszimális elemének vektoros területe, amelynek iránya a felületre merőleges

Egyenletes mágneses tér és sík felület esetén, ahol a mágneses tér a felület normáljával \\theta szöget zár be, a fluxus egyszerűbben számítható:

\\Phi\_B \= BA \\cos \\theta

ahol:

• B a mágneses tér erőssége
• A a felület területe

• \\theta a mágneses tér és a felület normáljának szöge

A Mágneses Fluxus Mértékegysége

A mágneses fluxus SI mértékegysége a weber (Wb). Egy weber egyenlő egy tesla szorozva egy négyzetméterrel (1 Wb = 1 T⋅m²). A korábbi CGS rendszerben a mágneses fluxus mértékegysége a maxwell (Mx) volt. Az átváltás a két egység között a következő: 1 Wb = 10^8 Mx.

A Mágneses Fluxus Fizikai Jelentősége

Faraday Indukciós Törvénye

A mágneses fluxus központi szerepet játszik az elektromágneses indukció jelenségének leírásában, amelyet Faraday indukciós törvénye fogalmaz meg. Ez a törvény kimondja, hogy egy zárt vezetőben indukált elektromotoros erő (EMF) egyenlő a vezetőt körülvevő mágneses fluxus időbeli változásának negatívjával:

\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}

Ez az alapvető törvény magyarázza meg az elektromos generátorok, transzformátorok és sok más elektromágneses eszköz működését.

Gauss Törvénye a Mágnesességre

A mágneses fluxus egy másik fontos összefüggése a Gauss törvénye a mágnesességre, amely a Maxwell-egyenletek egyike. Ez a törvény kimondja, hogy egy zárt felületen átmenő mágneses fluxus mindig nulla:

\\oint \\mathbf\{B\} \\cdot d\\mathbf\{A\} \= 0

Ez azt jelenti, hogy nincsenek mágneses monopólusok; a mágneses térvonalak mindig zárt hurkokat alkotnak.

A Mágneses Fluxus Mérése

Fluxusmérők

A mágneses fluxus közvetlen mérése speciális eszközökkel, úgynevezett fluxusmérőkkel történhet. Ezek az eszközök általában egy mérőtekercset és egy integrátort tartalmaznak. Amikor a mágneses fluxus megváltozik a mérőtekercsen keresztül, egy elektromotoros erő indukálódik, amelynek nagysága arányos a fluxus változásának sebességével. Az integrátor ezután kiszámítja a teljes fluxusváltozást.

Hall-effektus Szenzorok

A Hall-effektus szenzorok szintén használhatók a mágneses tér mérésére, amelyből aztán a fluxus is meghatározható, ha ismerjük a felületet, amelyen a tér áthalad. Ezek a szenzorok azon az elven működnek, hogy egy árammal átfolyatott vezetőben, amelyet egy mágneses térbe helyeznek, a töltött részecskékre a Lorentz-erő hat, ami feszültségkülönbséget hoz létre a vezető oldalain.

A Mágneses Fluxus Alkalmazásai

Elektromos Generátorok

Az elektromos generátorok a mágneses fluxus változásán alapulnak a villamos energia előállításához. Egy tekercset forgatnak egy mágneses térben, vagy egy mágneses teret mozgatnak egy tekercs körül, ami a tekercsen keresztülmenő mágneses fluxus időbeli változását eredményezi. Ez a változás elektromotoros erőt indukál a tekercsben, létrehozva ezzel elektromos áramot.

Transzformátorok

A transzformátorok két vagy több tekercsből állnak, amelyek egy közös mágneses magon helyezkednek el. Az egyik tekercsben (primer tekercs) folyó váltakozó áram változó mágneses fluxust hoz létre a magban. Ez a változó fluxus indukál egy elektromotoros erőt a másik tekercsben (szekunder tekercs), lehetővé téve a feszültség átalakítását.

Induktív Érzékelők

Számos induktív érzékelő működik a mágneses fluxus változásának elvén. Például a fémérzékelők változást észlelnek a mágneses fluxusban, amelyet egy fémtárgy közelsége okoz. Hasonló elven működnek az induktív közelségkapcsolók is.

Mágneses Adatrögzítés

A mágneses adatrögzítés, amelyet merevlemezeken és mágnescsíkos kártyákon használnak, szintén a mágneses fluxus elvén alapul. Az adatok a mágneses anyag kis területeinek mágnesezési irányának megváltoztatásával kerülnek rögzítésre. Az olvasófej érzékeli ezeknek a területeknek a mágneses fluxusát, és visszaalakítja azokat elektromos jelekké.

Összefoglalás

A mágneses fluxus egy alapvető fogalom az elektromágnesség területén, amely leírja a mágneses tér egy adott felületen való áthaladását. Számos fontos fizikai törvény és technológiai alkalmazás alapját képezi, beleértve az elektromágneses indukciót, az elektromos generátorokat, a transzformátorokat és a mágneses adatrögzítést. A mágneses fluxus megértése elengedhetetlen az elektromágneses jelenségek és az azokon alapuló technológiák mélyebb megértéséhez.

A Mágneses Fluxus Részletesebb Matematikai Megközelítése

A Felületi Integrál Jelentősége

A mágneses fluxus definíciójában szereplő felületi integrál (\\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}) kulcsfontosságú a fogalom pontos megértéséhez. Ez az integrál azt fejezi ki, hogy a mágneses fluxus a mágneses indukcióvektor és a felület infiniteszimális területeinek skaláris szorzatának összege a teljes felületen. A skaláris szorzat \(\\mathbf\{B\} \\cdot d\\mathbf\{A\} \= B dA \\cos \\theta\) figyelembe veszi a mágneses tér irányának és a felület orientációjának egymáshoz viszonyított helyzetét.

Nem Egyenletes Mágneses Tér Esetén

Ha a mágneses tér nem egyenletes a felületen, vagy ha a felület nem sík, akkor a fluxus kiszámításához a felületi integrált kell alkalmaznunk. Ekkor a felületet apró, dA területű elemekre bontjuk, minden egyes elemre kiszámítjuk a \\mathbf\{B\} \\cdot d\\mathbf\{A\} szorzatot, majd ezeket összegezzük (integráljuk) a teljes felületre.

Példa a Fluxus Számítására

Tekintsünk egy példát: egy A területű sík felületet egy egyenletes \\mathbf\{B\} mágneses térbe helyezünk. Ha a mágneses tér a felület normáljával \\theta szöget zár be, akkor a mágneses fluxus \\Phi\_B \= BA \\cos \\theta. Ha a mágneses tér párhuzamos a felület normáljával (\\theta \= 0^\\circ), akkor \\cos \\theta \= 1, és a fluxus maximális: \\Phi\_B \= BA. Ha a mágneses tér párhuzamos a felülettel (\\theta \= 90^\\circ), akkor \\cos \\theta \= 0, és a fluxus nulla.

A Mágneses Fluxus Változásának Következményei

Lenz Törvénye

Faraday indukciós törvényével szorosan összefügg a Lenz törvénye, amely megadja az indukált áram irányát. Lenz törvénye kimondja, hogy az indukált áram olyan irányú, hogy mágneses tere ellentétes a fluxusváltozást okozó mágneses tér változásával. Ez a negatív előjel Faraday törvényében (\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}) ennek a törvénynek a következménye.

Elektromágneses Erőterek

A változó mágneses fluxus elektromos erőteret hoz létre. Ez az összefüggés a Maxwell-egyenletek egyikében, a Faraday-féle indukciós törvény általánosított formájában jelenik meg:

\\oint \\mathbf\{E\} \\cdot d\\mathbf\{l\} \= \-\\frac\{d\}\{dt\} \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}

Ez az egyenlet azt mutatja, hogy egy zárt görbe mentén vett elektromos tér vonalintegrálja (az indukált elektromotoros erő) egyenlő a görbe által határolt felületen áthaladó mágneses fluxus időbeli változásának negatívjával.

További Alkalmazások és Koncepciók

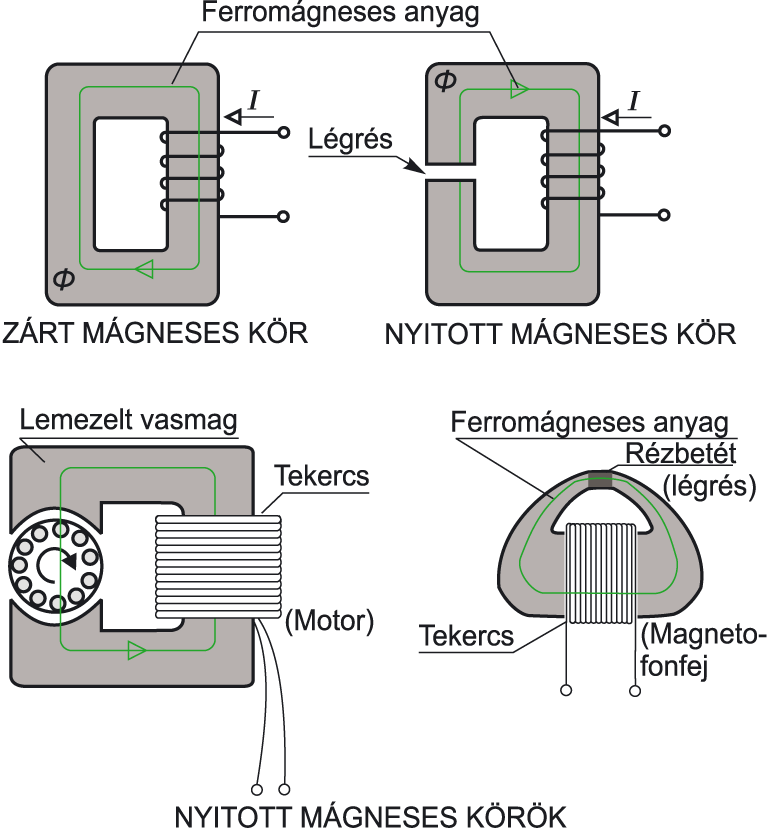
Mágneses Áramkörök

A mágneses fluxus fogalma a mágneses áramkörök analízisében is fontos szerepet játszik. A mágneses áramkörökben a mágneses fluxus analóg az elektromos árammal, a magnetomotoros erő (MMF) az elektromos feszültséggel, és a reluktancia az elektromos ellenállással. Ez az analógia segít a mágneses rendszerek, például elektromágnesek és transzformátorok tervezésében és elemzésében.

A Mágneses Fluxus Kvantálása

Bizonyos fizikai rendszerekben, például szupravezetőkben, a mágneses fluxus kvantált. Ez azt jelenti, hogy a fluxus csak bizonyos diszkrét értékeket vehet fel, amelyek a fluxuskvantum (\\Phi\_0 \= h / \(2e\) \\approx 2\.0678 \\times 10^\{\-15\} \\, \\text\{Wb\}) egész számú többszörösei. Ez a jelenség a szupravezetés kvantummechanikai természetének egyik megnyilvánulása.

A Mágneses Fluxus Szerepe a Kozmológiában

A mágneses fluxus a kozmológiában is felbukkan, például a csillagok és galaxisok mágneses terének kialakulásában és fenntartásában. A magnetohidrodinamika (MHD) a plazmák és más elektromosan vezető közegek mozgását és mágneses terét tanulmányozza, ahol a mágneses fluxus megőrzése fontos szerepet játszik.

Összegzés és Jövőbeli Kilátások

A mágneses fluxus továbbra is a fizika és a technológia egyik alapvető fogalma marad. Az elektromágneses jelenségek megértésének kulcsa, és számos modern technológia működésének alapját képezi. A kutatások folyamatosan új alkalmazásokat tárnak fel, például az anyagtudományban, az orvosi képalkotásban (MRI), és a kvantumtechnológiák területén. A mágneses fluxus pontos mérése és manipulálása a jövő technológiai fejlesztéseinek fontos területe lesz.

A Mágneses Fluxus és a Maxwell-egyenletek

A Maxwell-egyenletek Áttekintése

A Maxwell-egyenletek az elektromágnesség alapvető törvényeit foglalják össze. Négy egyenletből állnak, amelyek leírják, hogyan keletkezik és hogyan viselkedik az elektromos és mágneses tér, valamint azok kölcsönhatásait az elektromos töltésekkel és áramokkal. A mágneses fluxus fogalma több Maxwell-egyenletben is központi szerepet játszik.

Gauss Törvénye az Elektromossághoz

Bár nem közvetlenül a mágneses fluxussal kapcsolatos, érdemes megemlíteni a Gauss törvényét az elektromossághoz, amely kimondja, hogy egy zárt felületen átmenő elektromos fluxus arányos a felület által bezárt elektromos töltéssel:

\\oint \\mathbf\{E\} \\cdot d\\mathbf\{A\} \= \\frac\{Q\_\{enc\}\}\{\\epsilon\_0\}

Ez az egyenlet analóg a mágnesességre vonatkozó Gauss törvénnyel, de itt a forrás az elektromos töltés, míg a mágnesesség esetében nincsenek ismert mágneses monopólusok.

Faraday Indukciós Tör