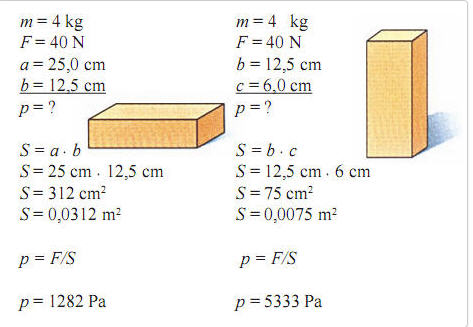
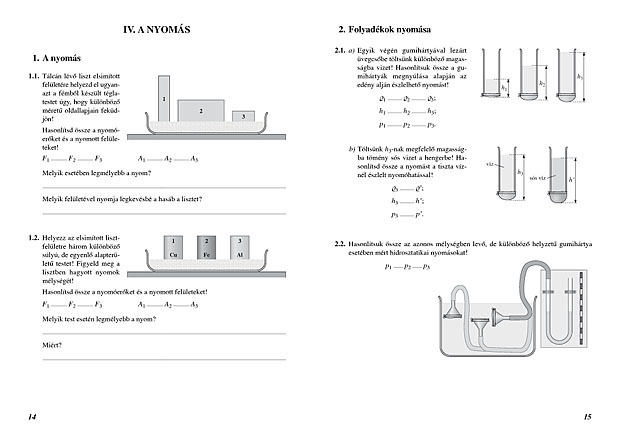
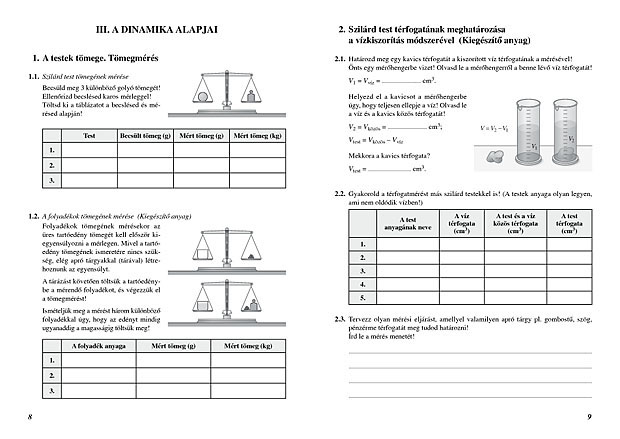
Fizika Feladatok 7 Osztaly Munka

Fizika Feladatok 7. Osztály: Munkavégzés, Energia és Teljesítmény – A Tudás Építőkövei

Üdvözöljük a hetedik osztályos fizika rejtelmeinek mélyére vezető utazásunkon! Ebben a részletes útmutatóban a munkavégzés, az energia és a teljesítmény alapvető fogalmait és alkalmazásait fogjuk feltárni, rengeteg gyakorlati feladaton keresztül. Célunk, hogy ne csupán megértsük ezeket a kulcsfontosságú fizikai mennyiségeket, hanem magabiztosan alkalmazzuk is őket a különböző problémák megoldása során. Készüljünk fel együtt arra, hogy a fizika izgalmas világában elmélyedjünk!

A Munkavégzés Fogalma és Számítása

A munkavégzés a fizikában akkor történik, ha egy erő elmozdít egy testet. Fontos hangsúlyozni, hogy nem minden erő okoz munkavégzést. Például, ha egy súlyos tárgyat tartunk a kezünkben, erőt fejtünk ki, de mivel a tárgy nem mozdul el, nem végzünk munkát a fizika értelmében. A munkavégzéshez tehát elengedhetetlen az erő hatására történő elmozdulás.

A munkavégzés ($W$) matematikailag az erő ($F$) és az elmozdulás ($s$) szorzatával adható meg, amennyiben az erő az elmozdulás irányába hat. Ha az erő nem párhuzamos az elmozdulással, akkor az erőnek az elmozdulás irányába eső komponensét kell figyelembe venni. Általánosan a munkavégzés képlete:

$$\mathbf{W = F \cdot s \cdot \cos(\alpha)}$$

ahol:

• $W$ a végzett munka (mértékegysége a Joule, J)
• $F$ a ható erő nagysága (mértékegysége a Newton, N)
• $s$ az elmozdulás nagysága (mértékegysége a méter, m)
• $\alpha$ az erő és az elmozdulás közötti szög

Példák a Munkavégzésre

1. Példa: Egyenes vonalú mozgás

Egy 10 N nagyságú erő egy vízszintes felületen 2 méteren keresztül húz egy testet. Mekkora munkát végez az erő, ha az erő és az elmozdulás iránya megegyezik?

Megoldás:

Adatok:

• $F = 10 \, \text{N}$

• $s = 2 \, \text{m}$
• $\alpha = 0^\circ$, így $\cos(0^\circ) = 1$

A munkavégzés:

$$\mathbf{W = F \cdot s \cdot \cos(\alpha) = 10 \, \text{N} \cdot 2 \, \text{m} \cdot 1 = 20 \, \text{J}}$$

Az erő által végzett munka 20 Joule.

2. Példa: Ferde erő hatása

Egy ember egy kötelet húz, amely 30 fokos szöget zár be a vízszintessel. A kötélben lévő erő 50 N, és a test 5 métert mozdul el a vízszintes talajon. Mekkora munkát végez az ember?

Megoldás:

Adatok:

• $F = 50 \, \text{N}$
• $s = 5 \, \text{m}$
• $\alpha = 30^\circ$, így $\cos(30^\circ) \approx 0.866$

A munkavégzés:

$$\mathbf{W = F \cdot s \cdot \cos(\alpha) = 50 \, \text{N} \cdot 5 \, \text{m} \cdot 0.866 \approx 216.5 \, \text{J}}$$

Az ember által végzett munka körülbelül 216.5 Joule.

Gyakorló Feladatok a Munkavégzéshez

1. Egy 25 N nagyságú erő egy testet 4 méteren keresztül tol el az erő irányában. Számítsa ki a végzett munkát!
2. Egy diák egy 0.5 kg tömegű könyvet felemel az asztalról a polcra, amely 1.5 méter magasan van. Mekkora munkát végez a diák a könyvön (a nehézségi erő ellenében)? (Ne feledje, hogy a nehézségi erő $F_g = m \cdot g$, ahol $g \approx 9.8 \, \text{m/s}^2$.)
3. Egy autó 5000 N nagyságú állandó erővel halad 100 métert egyenes úton. Mekkora munkát végez az autó motorja?
4. Egy labdát vízszintesen eldobunk. Végez-e munkát a nehézségi erő a pillanatban, amikor elhagyja a kezünket? Indokolja válaszát!

Az Energia Különböző Formái

Az energia a munkavégzésre való képesség. Számos formában létezik, és az egyik formából a másikba alakulhat át. A mechanikában kiemelten fontos a mozgási energia (kinetikus energia) és a helyzeti energia (potenciális energia).

Mozgási Energia (Kinetikus Energia)

A mozgási energia egy test mozgásából származó energia. Minél nagyobb egy test tömege és sebessége, annál nagyobb a mozgási energiája. A mozgási energia ($E_k$) képlete:

$$\mathbf{E_k = \frac{1}{2} m v^2}$$

ahol:

• $E_k$ a mozgási energia (mértékegysége a Joule, J)
• $m$ a test tömege (mértékegysége a kilogramm, kg)
• $v$ a test sebessége (mértékegysége a méter per szekundum, m/s)

Példa a Mozgási Energiára

Egy 2 kg tömegű labda 5 m/s sebességgel gurul. Mekkora a labda mozgási energiája?

Megoldás:

Adatok:

• $m = 2 \, \text{kg}$
• $v = 5 \, \text{m/s}$

A mozgási energia:

$$\mathbf{E_k = \frac{1}{2} \cdot 2 \, \text{kg} \cdot (5 \, \text{m/s})^2 = 1 \, \text{kg} \cdot 25 \, \text{m}^2/\text{s}^2 = 25 \, \text{J}}$$

A labda mozgási energiája 25 Joule.

Helyzeti Energia (Potenciális Energia)

A helyzeti energia egy test helyzetéből vagy állapotából származó energia. A gravitációs mezőben lévő testeknek gravitációs helyzeti energiájuk van a magasságuktól függően. A rugalmasan deformált testeknek (pl. megfeszített rugó) rugalmas helyzeti energiájuk van.

Gravitációs Helyzeti Energia

A $h$ magasságban lévő, $m$ tömegű test gravitációs helyzeti energiája ($E_p$) a következőképpen számítható:

$$\mathbf{E_p = m \cdot g \cdot h}$$

ahol:

• $E_p$ a gravitációs helyzeti energia (mértékegysége a Joule, J)
• $m$ a test tömege (mértékegysége a kilogramm, kg)
• $g$ a gravitációs gyorsulás (a Földön körülbelül $9.8 \, \text{m/s}^2$)
• $h$ a test magassága egy referencia szinthez képest (mértékegysége a méter, m)

Példa a Gravitációs Helyzeti Energiára

Egy 3 kg tömegű könyv egy 2 méter magas polcon van. Mekkora a könyv gravitációs helyzeti energiája a talajhoz képest?

Megoldás:

Adatok:

• $m = 3 \, \text{kg}$
• $g = 9.8 \, \text{m/s}^2$
• $h = 2 \, \text{m}$

A gravitációs helyzeti energia:

$$\mathbf{E_p = 3 \, \text{kg} \cdot 9.8 \, \text{m/s}^2 \cdot 2 \, \text{m} = 58.8 \, \text{J}}$$

A könyv gravitációs helyzeti energiája a talajhoz képest 58.8 Joule.

Rugalmas Helyzeti Energia

Egy megnyújtott vagy összenyomott rugóban tárolt rugalmas helyzeti energia ($E_{rug}$) a rugó megnyúlásának vagy összenyomásának négyzetével arányos:

$$\mathbf{E_{rug} = \frac{1}{2} k x^2}$$

ahol:

• $E_{rug}$ a rugalmas helyzeti energia (mértékegysége a Joule, J)
• $k$ a rugóállandó (mértékegysége a Newton per méter, N/m)
• $x$ a rugó megnyúlása vagy összenyomása az egyensúlyi helyzetéhez képest (mértékegysége a méter, m)

Példa a Rugalmas Helyzeti Energiára

Egy rugó rugóállandója $k = 100 \, \text{N/m}$. Mekkora a rugóban tárolt rugalmas helyzeti energia, ha 0.1 méterrel megnyújtjuk?

Megoldás:

Adatok:

• $k = 100 \, \text{N/m}$
• $x = 0.1 \, \text{m}$

A rugalmas helyzeti energia:

$$\mathbf{E_{rug} = \frac{1}{2} \cdot 100 \, \text{N/m} \cdot (0.1 \, \text{m})^2 = \frac{1}{2} \cdot 100 \cdot 0.01 \, \text{J} = 0.5 \, \text{J}}$$

A rugóban tárolt rugalmas helyzeti energia 0.5 Joule.

Gyakorló Feladatok az Energiához

1. Egy 5 kg tömegű test 10 m/s sebességgel mozog. Mekkora a mozgási energiája?
2. Egy 0.2 kg tömegű alma egy 3 méter magas fáról esik le. Mekkora volt az alma gravitációs helyzeti energiája a fa tetején a talajhoz képest?
3. Egy rugó rugóállandója 200 N/m. Mekkora a rugóban tárolt energia, ha 0.05 méterrel összenyomjuk?
4. Egy autó tömege 1200 kg, és 20 m/s sebességgel halad. Mekkora a mozgási energiája?

Az Energiamegmaradás Törvénye

Az energiamegmaradás törvénye az egyik legfontosabb elv a fizikában. Kimondja, hogy egy zárt rendszer teljes energiája állandó marad, az energia nem vész el és nem keletkezik a semmiből, csupán átalakulhat egyik formából a másikba.

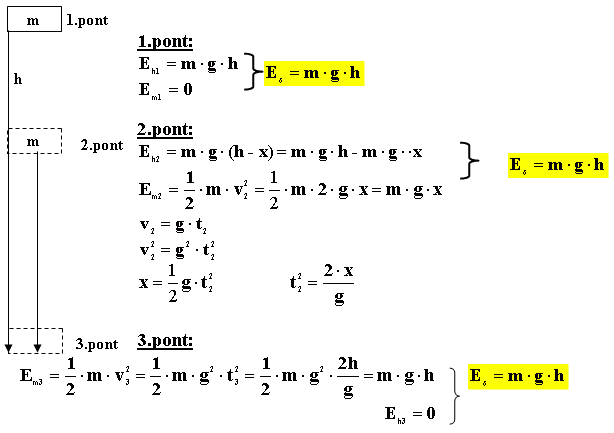
Például, amikor egy labdát feldobunk, a kezdeti mozgási energiája fokozatosan gravitációs helyzeti energiává alakul át, ahogy emelkedik. A legmagasabb ponton, ahol a sebessége nulla, minden mozgási energia helyzeti energiává alakult. Amikor a labda leesik, a helyzeti energia ismét mozgási energiává alakul át.

Példa az Energiamegmaradásra

Egy 1 kg tömegű testet 10 méter magasról elejtünk. Mekkora lesz a sebessége a földbe csapódás pillanatában (a légellenállástól eltekintve)?

Megoldás:

A kezdeti állapotban a testnek csak helyzeti energiája van:

$$E_{p1} = m \cdot g \cdot h = 1 \, \text{kg} \cdot 9.8 \, \text{m/s}^2 \cdot 10 \, \text{m} = 98 \, \text{J}$$

A kezdeti mozgási energia nulla: $E_{k1} = 0 \, \text{J}$.

A földbe csapódás pillanatában a magasság nulla, így a helyzeti energia nulla: $E_{p2} = 0 \, \text{J}$. A teljes energia ekkor a mozgási energiával egyenlő:

$$E_{k2} = \frac{1}{2} m v^2$$

Az energiamegmaradás törvénye szerint a kezdeti teljes energia egyenlő a végső teljes energiával:

$$E_{p1} + E_{k1

Mozgasi Energia Mertekegysege

A Mozgási Energia Mértékegysége: A Kinetikus Energia Részletes Feltárása

Ebben az átfogó cikkben részletesen megvizsgáljuk a mozgási energia mértékegységét, elmélyedünk a kinetikus energia fogalmában, annak fizikai jelentőségében, és bemutatjuk, hogyan számíthatjuk ki a mozgó testek energiáját. Célunk, hogy egy olyan kimerítő útmutatót nyújtsunk, amely minden kérdésre választ ad a témával kapcsolatban, legyen szó diákokról, tanárokról vagy a fizika iránt érdeklődőkről.

Mi az a Mozgási Energia (Kinetikus Energia)?

A mozgási energia, más néven kinetikus energia, az a munka, amely egy testet nyugalmi állapotból egy adott sebességre gyorsít fel. Képzeljünk el egy álló autót, amelyet eltolunk. Ahhoz, hogy az autó mozogni kezdjen, munkát kell végeznünk rajta, energiát kell befektetnünk. Ez a befektetett energia alakul át az autó mozgási energiájává. Minél nagyobb a test tömege és minél nagyobb a sebessége, annál nagyobb a mozgási energiája.

A Kinetikus Energia Fogalmának Mélyebb Értelmezése

A kinetikus energia nem más, mint a testek mozgásából származó energia. Ez egy skaláris mennyiség, ami azt jelenti, hogy csak nagysága van, iránya nincs. A kinetikus energia szorosan kapcsolódik a test impulzusához és a munkatételhez. A munkatétel kimondja, hogy egy testre ható összes erő által végzett munka egyenlő a test kinetikus energiájának megváltozásával.

Történelmi Áttekintés: A Mozgási Energia Koncepciójának Fejlődése

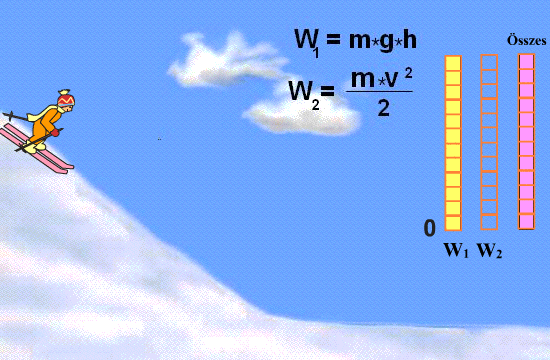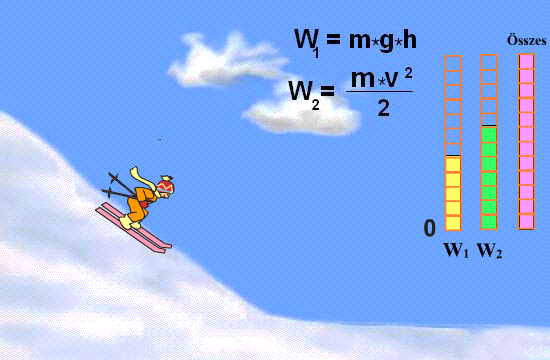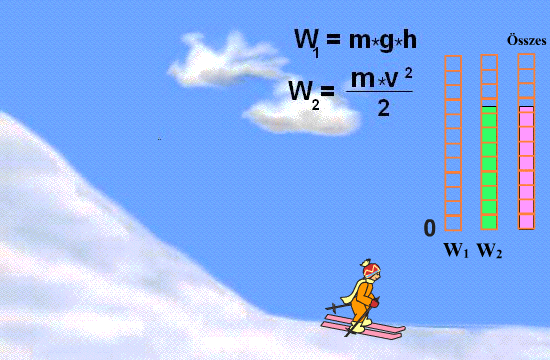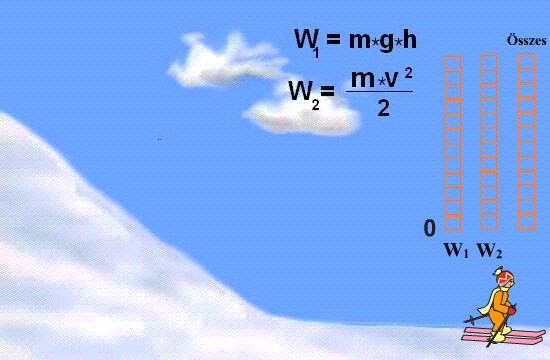
A mozgási energia fogalmának megértése évszázadokig tartó tudományos munka eredménye. Már a korai gondolkodók is felismerték a mozgás és az erő közötti kapcsolatot. A 17. században olyan tudósok, mint Galileo Galilei és Isaac Newton, lefektették a klasszikus mechanika alapjait, amelyek elengedhetetlenek a kinetikus energia pontos leírásához. A vis viva (élő erő) fogalma, amelyet Gottfried Wilhelm Leibniz és mások fejlesztettek ki, a kinetikus energia korai előfutárának tekinthető. A modern értelemben vett kinetikus energia fogalma a 19. században, a termodinamika és az energiamegmaradás törvényének kidolgozásával nyert végleges formát.

A Mozgási Energia Mértékegysége: A Joule

A mozgási energia (és általában mindenféle energia) nemzetközi mértékegységrendszerben (SI) mértékegysége a joule, amelyet James Prescott Joule angol fizikus tiszteletére neveztek el. A joule (J) egy származtatott SI-egység, amelyet az alapegységekkel a következőképpen fejezhetünk ki:

\\text\{1 J\} \= \\text\{1 kg\} \\cdot \\left\(\\frac\{\\text\{m\}\}\{\\text\{s\}\}\\right\)^2 \= \\text\{1 kg\} \\cdot \\text\{m\}^2 \\cdot \\text\{s\}^\{\-2\}

Ez azt jelenti, hogy egy joule az a munkamennyiség, amely ahhoz szükséges, hogy egy 1 kilogramm tömegű testet 1 méter per szekundum sebességre gyorsítsunk fel nyugalmi állapotból (bár ez nem a legközvetlenebb definíciója a joule-nak, de segít megérteni a kapcsolatot a tömeg, a sebesség és az energia között a kinetikus energia szempontjából). Pontosabban, egy joule az a munka, amelyet akkor végzünk, ha egy 1 newton nagyságú erőt 1 méter távolságon keresztül fejtünk ki az erő irányában.

A Joule Kapcsolata Más Mértékegységekkel

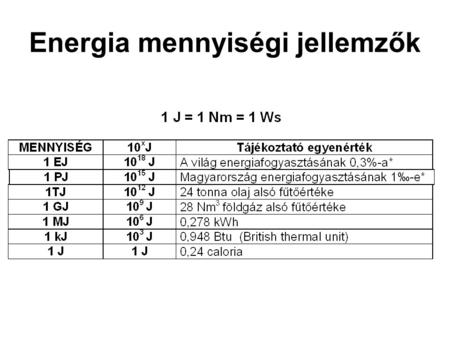
Fontos megérteni, hogy a joule nem csak a mozgási energia mértékegysége, hanem mindenféle energiáé, beleértve a potenciális energiát, a hőenergiát, a elektromágneses energiát stb. Gyakran találkozhatunk más energiamértékegységekkel is, mint például a kalória (cal) vagy a kilowattóra (kWh), de a tudományos és technikai területen az SI-rendszerbeli joule az elfogadott és preferált egység.

• 1 kalória (cal) ≈ 4,184 joule (J)
• 1 kilokalória (kcal) = 1000 kalória ≈ 4184 joule (J)
• 1 kilowattóra (kWh) = 3,6 × 10⁶ joule (J)

A Mozgási Energia Kiszámítása

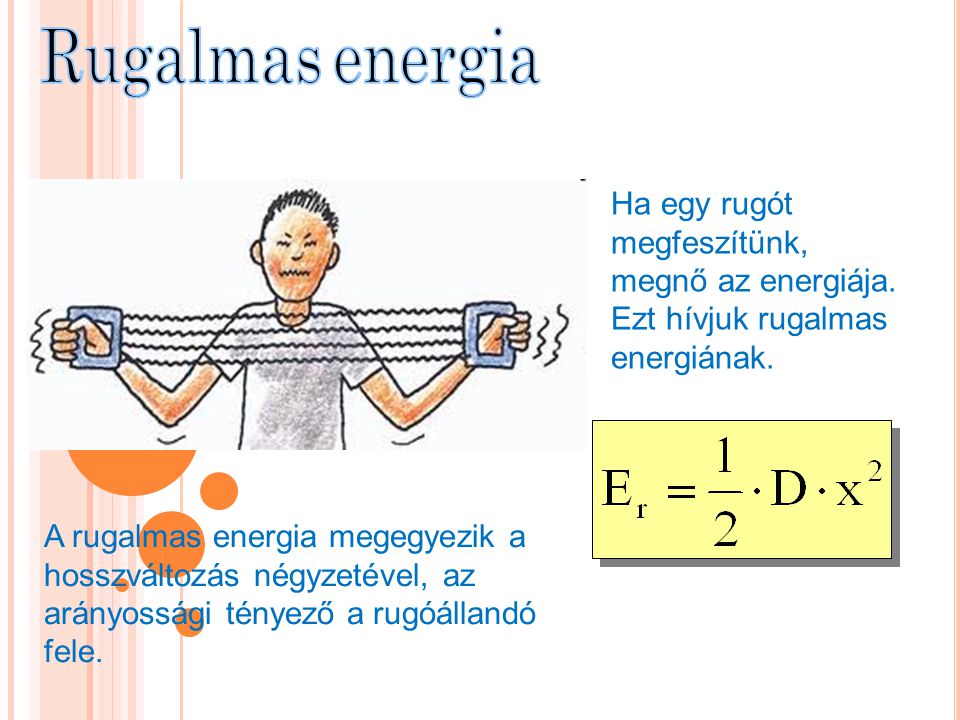
A mozgási energia (E\_k) kiszámításának képlete rendkívül fontos a fizikában:

E\_k \= \\frac\{1\}\{2\} m v^2

Ahol:

• E\_k a mozgási energia (joule-ban)
• m a test tömege (kilogrammban)
• v a test sebessége (méter per szekundumban)

Ez az egyenlet azt mutatja, hogy a mozgási energia egyenesen arányos a test tömegével, és a sebesség négyzetével. Ez azt jelenti, hogy ha egy test sebessége kétszeresére nő, a mozgási energiája négyszeresére nő (ugyanazon tömeg mellett).

Példák a Mozgási Energia Számítására

1. Példa: Egy futó ember mozgási energiája

Egy 70 kg tömegű ember 5 m/s sebességgel fut. Számítsuk ki a mozgási energiáját!

E\_k \= \\frac\{1\}\{2\} \\cdot 70 \\text\{ kg\} \\cdot \(5 \\text\{ m/s\}\)^2 \= \\frac\{1\}\{2\} \\cdot 70 \\cdot 25 \\text\{ J\} \= 35 \\cdot 25 \\text\{ J\} \= 875 \\text\{ J\}

Tehát a futó ember mozgási energiája 875 joule.

2. Példa: Egy autó mozgási energiája

Egy 1000 kg tömegű autó 20 m/s sebességgel halad. Mekkora a mozgási energiája?

E\_k \= \\frac\{1\}\{2\} \\cdot 1000 \\text\{ kg\} \\cdot \(20 \\text\{ m/s\}\)^2 \= \\frac\{1\}\{2\} \\cdot 1000 \\cdot 400 \\text\{ J\} \= 500 \\cdot 400 \\text\{ J\} \= 200000 \\text\{ J\} \= 200 \\text\{ kJ\}

Az autó mozgási energiája 200 kilojoule.

3. Példa: Egy labda eldobása

Egy 0,5 kg tömegű labdát 10 m/s sebességgel eldobunk. Mennyi a labda mozgási energiája?

E\_k \= \\frac\{1\}\{2\} \\cdot 0,5 \\text\{ kg\} \\cdot \(10 \\text\{ m/s\}\)^2 \= \\frac\{1\}\{2\} \\cdot 0,5 \\cdot 100 \\text\{ J\} \= 0,25 \\cdot 100 \\text\{ J\} \= 25 \\text\{ J\}

A labda mozgási energiája 25 joule.

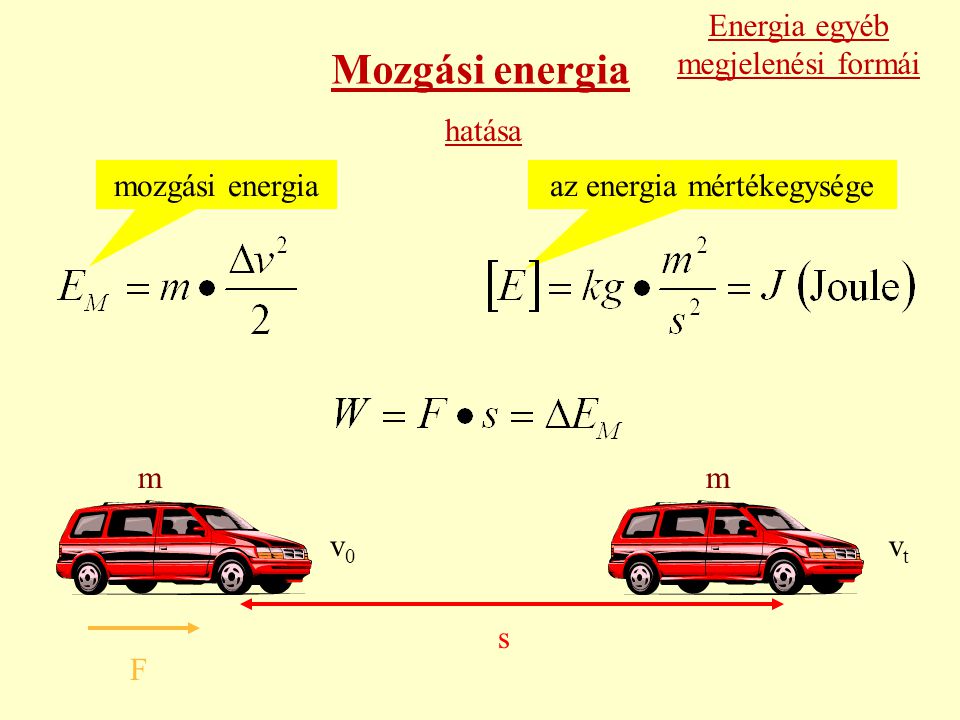
A Mozgási Energia és a Munka Kapcsolata

A munka-energia tétel alapvető fontosságú a fizika megértésében. Kimondja, hogy egy testre ható összes erő által végzett munka egyenlő a test kinetikus energiájának megváltozásával. Matematikailag:

W\_\{összes\} \= \\Delta E\_k \= E\_\{k,vég\} \- E\_\{k,kezdet\}

Ahol W\_\{összes\} a testre ható összes erő által végzett munka, \\Delta E\_k pedig a kinetikus energia megváltozása.

Példa a Munka-Energia Tételre

Egy álló 2 kg tömegű testre egy 10 N nagyságú, vízszintes erő hat 3 méteren keresztül. Mekkora lesz a test sebessége a 3 méter megtétele után?

1. A végzett munka kiszámítása: W \= F \\cdot d \= 10 \\text\{ N\} \\cdot 3 \\text\{ m\} \= 30 \\text\{ J\}.
2. A munka-energia tétel alkalmazása: W \= \\Delta E\_k \= E\_\{k,vég\} \- E\_\{k,kezdet\}. Mivel a test kezdetben nyugalomban volt, E\_\{k,kezdet\} \= 0. Tehát 30 \\text\{ J\} \= E\_\{k,vég\}.
3. A végső kinetikus energia képletének felhasználása a sebesség meghatározásához: E\_\{k,vég\} \= \\frac\{1\}\{2\} m v^2.

   30 \\text\{ J\} \= \\frac\{1\}\{2\} \\cdot 2 \\text\{ kg\} \\cdot v^2

   30 \= v^2

   v \= \\sqrt\{30\} \\text\{ m/s\} \\approx 5,48 \\text\{ m/s\}

   Tehát a test sebessége a 3 méter megtétele után körülbelül 5,48 m/s lesz.

A Mozgási Energia Különböző Formái és Kontextusai

A mozgási energia nem csak a lineáris mozgáshoz kapcsolódik. Megkülönböztethetünk más formáit is:

Rotációs Kinetikus Energia

A forgó testeknek is van mozgási energiájuk, amelyet rotációs kinetikus energiának nevezünk. Ez az energia a test tehetetlenségi nyomatékától (I) és szögsebességétől (\\omega) függ:

E\_\{rot\} \= \\frac\{1\}\{2\} I \\omega^2

Például egy forgó keréknek vagy egy pörgő korcsolyázónak van rotációs kinetikus energiája.

Rezgési Kinetikus Energia

A rezgő rendszerekben, mint például egy rugón lévő tömeg vagy egy hanghullám, az energia periodikusan alakul át potenciális és kinetikus energia között. A rezgési kinetikus energia a rezgő testek mozgásához kapcsolódik.

A Mozgási Energia Jelentősége a Különböző Területeken

A Közlekedésben

A közlekedési eszközök, mint az autók, vonatok, repülők, mind mozgási energiával rendelkeznek. A mozgási energia növeléséhez munkát kell végezni (pl. a motor által), a mozgási energia csökkentéséhez pedig fékezésre van szükség, amely során a mozgási energia más formákká (főként hővé) alakul át.

Az Ipari Termelésben

Számos ipari folyamat során a mozgási energia kulcsfontosságú. Gépek, szerszámok működnek mozgási energia segítségével, legyen szó forgó alkatrészekről, szállítószalagokról vagy megmunkáló eszközökről.

A Természetben

A természetben is mindenütt jelen van a mozgási energia. A szél mozgása (szélenergia), a víz áramlása (vízienergia), a hullámok mozgása (hullámenergia) mind a mozgási energia megnyilvánulásai. Az élőlények mozgása, a bolygók keringése a Nap körül szintén a mozgási energiához köthető.

A Mozgási Energia Megőrzése

Egy zárt rendszerben, ahol nincsenek disszipatív erők (mint például a súrlódás), a teljes mechanikai energia (a potenciális és a kinetikus energia összege) megmarad. Bár a kinetikus energia potenciális energiává alakulhat és fordítva, a kettő összege állandó marad. Ez az energiamegmaradás elve.

Példa az Energiamegmaradásra

Egy inga lengése során a legalsó ponton a potenciális energia a legkisebb (ha a nullszintet itt vesszük), és a kinetikus energia a legnagyobb. A legmagasabb pontokon pedig a kinetikus energia nulla (a pillanatnyi megállás miatt), és a potenciális energia a legnagyobb. A köztes pontokon az energia részben kinetikus, részben potenciális, de a kettő összege (ha nincsenek veszteségek) állandó.

Gyakran Ismételt Kérdések a Mozgási Energiával Kapcsolatban

Mi a különbség a mozgási energia és a potenciális energia között?

A mozgási energia egy test mozgásából származik, míg a potenciális energia a test helyzetéből vagy állapotából adódik (pl. gravitációs potenciális energia a magasságtól függ, rugalmas potenciális energia a rugó megnyúlásától).

Milyen tényezőktől függ a mozgási energia?

A mozgási energia két fő tényezőtől függ: a test tömegétől és a sebességének négyzetétől.

Lehet-e a mozgási energia negatív?

Nem, a mozgási energia mindig nemnegatív. A tömeg (m) mindig pozitív, és a sebesség négyzete (v^2) is mindig nemnegatív.

Mi a mozgási energia mértékegysége?

A mozgási energia mértékegysége a joule (J) a Nemzetközi Mértékegységrendszerben (SI).

Összefoglalás

A mozgási energia, vagy kinetikus energia, egy test mozgásának köszönhető energia. Mértékegysége a joule (J). Kiszámítása a E\_k \= \\frac\{1\}\{2\} m v^2 képlettel történik, ahol m a tömeg és v a sebesség. A mozgási energia alapvető fogalom a fizikában, és számos területen fontos szerepet játszik, a közlekedéstől a természeti jelenségekig. A munka-energia tétel és az energiamegmaradás elve segít megérteni a mozgási energia és más energiaformák közötti kapcsolatot.

További Olvasmányok és Források

• Fizika tankönyvek
• Online fizika kurzusok
• Tudományos cikkek a mechanikáról

Reméljük, hogy ez a részletes útmutató segített megérteni a mozg

Joule Kilojoule Atvaltas

Joule Kilojoule Átváltás: A Teljes Útmutató

Ebben a részletes útmutatóban mélyrehatóan megvizsgáljuk a joule (J) és a kilojoule (kJ) közötti kapcsolatot. Célunk, hogy minden olvasó számára érthetővé tegyük ezt az alapvető energiaegység-átváltást, legyen szó fizikáról tanuló diákról, mérnökről vagy bárkiről, akinek szüksége van erre az ismeretre. Bemutatjuk a pontos átváltási képleteket, számos gyakorlati példán keresztül illusztráljuk a használatukat, és praktikus tanácsokat adunk a mindennapi alkalmazáshoz.

Mi az a Joule? Az Energia Alapegysége

A joule a Nemzetközi Mértékegységrendszerben (SI) az energia, a munka vagy a hő mennyiségének származtatott egysége. Nevét James Prescott Joule angol fizikusról kapta. Egy joule egyenlő azzal a munkával, amelyet akkor végzünk, ha egy newton erővel egy méteren keresztül mozgatunk egy tárgyat. Alapegységekkel kifejezve: $\text{1 J} = \text{1 kg} \cdot \text{m}^2 \cdot \text{s}^{ -2}$. A joule rendkívül sokoldalú egység, amelyet a fizika számos területén használnak, beleértve a mechanikát, a termodinamikát, az elektromosságot és a mágnesességet.

A Joule gyakorlati jelentősége

A joule nem csupán egy elméleti fogalom; a mindennapi életünkben is gyakran találkozhatunk vele. Például az élelmiszerek energiatartalmát gyakran kilojoule-ban adják meg, de a mögöttük álló alapvető egység a joule. Egy elektromos készülék által felhasznált energia mennyiségét is joule-ban vagy annak többszörösében mérjük. A fizikai kísérletek és a mérnöki tervezés során a joule pontos ismerete elengedhetetlen a számításokhoz és a rendszerek megértéséhez.

Mi az a Kilojoule? A Joule Nagyobb Egysége

A kilojoule (kJ) a joule egy többszöröse, pontosan ezerszerese. A “kilo-” előtag a görög eredetű “khilioi” szóból származik, ami ezret jelent. Tehát: $\text{1 kJ} = 1000 \text{ J}$. A kilojoule-t gyakran használják nagyobb energiamennyiségek kifejezésére, mivel a joule bizonyos esetekben túl kicsi egységnek bizonyulna a praktikus használathoz. Ilyen területek például az élelmiszeripar, a fűtés és a nagyipari energiafelhasználás.

A Kilojoule szerepe a mindennapi életben

Amikor egy élelmiszer csomagolásán látjuk az energiatartalmat, az szinte mindig kilojoule-ban van megadva. Ez sokkal praktikusabb, mint nagyszámú joule-t írni. Például egy átlagos felnőtt napi energiaigénye körülbelül 8000-10000 kJ. A fűtési rendszerek teljesítményét is gyakran kilojoule per órában (kJ/h) adják meg. A kilojoule tehát egy fontos egység a nagyobb léptékű energiafogyasztás és -termelés leírására.

A Joule és Kilojoule közötti alapvető átváltás

Az átváltás a két egység között rendkívül egyszerű. Mivel $\text{1 kJ} = 1000 \text{ J}$, ezért:

• Joule-ból kilojoule-ba váltáshoz a joule értéket el kell osztanunk 1000-rel: $$\text{kJ} = \frac{\text{J}}{1000}$$
• Kilojoule-ból joule-ba váltáshoz a kilojoule értéket meg kell szoroznunk 1000-rel: $$\text{J} = \text{kJ} \times 1000$$

Ez az egyszerű szorzás vagy osztás teszi lehetővé, hogy könnyedén váltsunk a két mértékegység között, attól függően, hogy éppen melyik a legmegfelelőbb a kontextusban.

Példák a Joule-Kilojoule átváltásra

Nézzünk néhány gyakorlati példát az átváltás megértéséhez:

• Ha egy rendszer energiája 5000 joule, akkor ez kilojoule-ban: $$\frac{5000 \text{ J}}{1000} = 5 \text{ kJ}$$
• Ha egy élelmiszer energiatartalma 250 kJ, akkor ez joule-ban: $$250 \text{ kJ} \times 1000 = 250000 \text{ J}$$

• Egy 12000 joule energiájú folyamat kilojoule-ban kifejezve: $$\frac{12000 \text{ J}}{1000} = 12 \text{ kJ}$$
• Ha egy fűtőberendezés 3,6 MJ (megajoule, ahol 1 MJ = 1 000 000 J) energiát termel óránként, ez kilojoule-ban óránként: $$\frac{3600000 \text{ J}}{1000} = 3600 \text{ kJ/h}$$

Ezek a példák jól szemléltetik, hogyan alkalmazhatjuk a fenti egyszerű képleteket a gyakorlatban.

Mikor melyik egységet használjuk?

A választás a joule és a kilojoule között gyakran a kényelemtől és a kontextustól függ. Általánosságban elmondható, hogy kisebb energiamennyiségek esetén a joule a praktikusabb, míg nagyobb mennyiségeknél a kilojoule használata áttekinthetőbbé teszi a számokat.

A Joule használata

A joule gyakran előfordul a fizikai alapelvek leírásakor, például a munkatétel vagy az energia megmaradásának törvénye kapcsán. Kisebb léptékű kísérletek és számítások során, ahol az energiamennyiségek nem túl nagyok, a joule a természetes választás. Például egy kondenzátorban tárolt energia, egy rugóban tárolt potenciális energia vagy egy apró részecske kinetikus energiája gyakran joule-ban kerül kifejezésre.

A Kilojoule használata

A kilojoule elterjedtebb a mindennapi alkalmazásokban és a nagyobb léptékű rendszerek leírásakor. Az élelmiszeriparban szinte kizárólag kilojoule-ban adják meg az energiatartalmat. A fűtés, a légkondicionálás és az ipari folyamatok energiafelhasználását is gyakran kilojoule-ban vagy még nagyobb egységekben (pl. megajoule, gigajoule) szokás megadni. Ez segít elkerülni a nagyon nagy számokat, amelyek nehezen áttekinthetők lennének joule-ban kifejezve.

Részletes áttekintés: A Joule eredete és definíciója

Ahogy korábban említettük, a joule James Prescott Joule munkásságának állít emléket. Joule kísérletei a hő és a mechanikai munka közötti kapcsolatra fókuszáltak, és kulcsszerepet játszottak az energiamegmaradás elvének megértésében. A joule SI-definíciója a következőképpen alakul:

$$\text{1 J} = 1 \frac{\text{kg} \cdot \text{m}^2}{\text{s}^2} = 1 \text{ N} \cdot \text{m} = 1 \text{ W} \cdot \text{s}$$

Ahol:

• N a newton (az erő egysége)
• m a méter (a távolság egysége)
• W a watt (a teljesítmény egysége)

• s a másodperc (az idő egysége)

Ez a definíció rávilágít a joule sokoldalúságára és arra, hogy hogyan kapcsolódik más alapvető fizikai mennyiségekhez.

A Joule kapcsolata más energiaegységekkel

Érdemes megemlíteni, hogy a joule nem az egyetlen energiaegység. Gyakran találkozhatunk más egységekkel is, mint például a kalória (cal), a kilowattóra (kWh) vagy az elektronvolt (eV). Az alábbiakban röviden összefoglaljuk ezek kapcsolatát a joule-lal:

• 1 kalória (cal) ≈ 4,184 joule (J)
• 1 kilokalória (kcal) = 1000 cal ≈ 4184 joule (J)
• 1 kilowattóra (kWh) = 3,6 × 10^6 joule (J)
• 1 elektronvolt (eV) ≈ 1,602 × 10^-19 joule (J)

Bár ezek az egységek különböző területeken elterjedtek, a joule az SI-rendszer alapvető energiaegysége, így minden más energiaegység végső soron kifejezhető joule-ban.

Részletes áttekintés: A Kilojoule használatának előnyei

A kilojoule használatának fő előnye a nagyobb energiamennyiségek kezelésének egyszerűsítése. Ahelyett, hogy nagy számokkal dolgoznánk joule-ban, a kilojoule lehetővé teszi, hogy kisebb, könnyebben kezelhető számokat használjunk. Ez különösen fontos a kereskedelemben, az iparban és a mindennapi kommunikációban.

Kilojoule az élelmiszeriparban

Az élelmiszerek energiatartalmának jelölése szinte mindenhol kilojoule-ban történik. Ez megkönnyíti a fogyasztók számára az egyes termékek energiatartalmának összehasonlítását és a napi energiabevitelük nyomon követését. Egy átlagos táplálkozási címkén az energiaérték kJ-ban és gyakran kcal-ban is meg van adva.

Kilojoule a fűtés- és légkondicionálástechnikában

A fűtőberendezések és légkondicionálók teljesítményét gyakran kilojoule per órában (kJ/h) vagy kilowattban (kW, ahol 1 kW = 3600 kJ/h) adják meg. Ez a mértékegység segít a felhasználóknak megérteni, hogy mennyi energiát képes leadni vagy felvenni az adott berendezés egy óra alatt, ami fontos a megfelelő készülék kiválasztásához és az energiafogyasztás becsléséhez.

Gyakorlati feladatok: Joule és Kilojoule átváltás

Most nézzünk néhány gyakorlati feladatot, hogy még jobban rögzüljön az átváltás:

1. Válts át 7500 joule-t kilojoule-ba.
2. Válts át 3,2 kilojoule-t joule-ba.
3. Egy folyamat 150000 joule energiát igényel. Hány kilojoule ez?
4. Egy élelmiszer energiatartalma 920 kJ. Hány joule ez?

A feladatok megoldásai

1. $$7500 \text{ J} \div 1000 = 7,5 \text{ kJ}$$
2. $$3,2 \text{ kJ} \times 1000 = 3200 \text{ J}$$
3. $$150000 \text{ J} \div 1000 = 150 \text{ kJ}$$
4. $$920 \text{ kJ} \times 1000 = 920000 \text{ J}$$

Reméljük, ezek a feladatok segítettek jobban megérteni az átváltást a két egység között.

Online Joule-Kilojoule átváltó eszköz

Azonnali átváltáshoz használhatod online átváltó eszközünket:

Kérjük, add meg az átváltandó értéket:

Joule:

kJ

Kilojoule:

J

Összefoglalás: A Joule és Kilojoule fontossága

A joule és a kilojoule alapvető energiaegységek, amelyek elengedhetetlenek a fizikai és mérnöki tudományokban, valamint a mindennapi élet számos területén. A kettő közötti egyszerű átváltás lehetővé teszi számunkra, hogy a kontextusnak leginkább megfelelő egységet használjuk az energiamennyiségek kifejezésére. Reméljük, ez a részletes útmutató segített tisztázni a joule és a kilojoule közötti kapcsolatot és azok gyakorlati alkalmazásait.

További információk és források

• SI alapegységek: [Link egy megbízható forráshoz]
• Energia mértékegységei: [Link egy megbízható forráshoz]

Gyakran Ismételt Kérdések (GYIK)

Hány joule egy kilojoule?

Egy kilojoule pontosan 1000 joule.

Mikor érdemes kilojoule-t használni?

Nagyobb energiamennyiségek kifejezésére, például élelmiszerek energiatartalmának vagy fűtési rendszerek teljesítményének megadásakor.

Mi a joule SI-definíciója?

1 joule = 1 kg ⋅ m²/s².

Köszönjük, hogy elolvastad útmutatónkat!