Energiamegmaradas Torvenye Mozaik

Az Energiamegmaradás Törvénye: A Természet Egyetemes Alapelve

Az energiamegmaradás törvénye a fizika egyik legfontosabb és legalapvetőbb elve, amely azt mondja ki, hogy egy zárt rendszer teljes energiája időben állandó marad. Ez azt jelenti, hogy az energia nem teremthető és nem pusztítható el, csupán egyik formából a másikba alakulhat át. Ez az elv áthatja a természettudományok szinte minden területét, a mikroszkopikus részecskék kölcsönhatásaitól kezdve a kozmikus jelenségekig.

Az Energiamegmaradás Törvényének Tudományos Alapjai

Az energiamegmaradás törvényének gyökerei a 19. század közepére nyúlnak vissza, amikor olyan tudósok, mint Julius Robert Mayer, James Prescott Joule és Hermann von Helmholtz egymástól függetlenül jutottak hasonló következtetésekre a munka és a hő kapcsolatát vizsgálva. Munkájuk révén vált világossá, hogy a hő egyfajta energia, és hogy a mechanikai munka hővé alakítható, és fordítva, miközben a rendszer teljes energiája megmarad.

A Termodinamika Első Főtételének Kapcsolata az Energiamegmaradással

A termodinamika első főtétele az energiamegmaradás törvényének egyik formális megfogalmazása termodinamikai rendszerekre. Kimondja, hogy egy zárt rendszer belső energiájának megváltozása egyenlő a rendszerrel közölt hő és a rendszeren végzett munka összegével:

$$\Delta U = Q – W$$

ahol $\Delta U$ a belső energia megváltozása, $Q$ a rendszerrel közölt hő, és $W$ a rendszer által végzett munka. Ez az egyenlet rögzíti, hogy az energia nem vész el, hanem a rendszer és a környezete között cserélődik hő és munka formájában.

A Noether-tétel és az Energiamegmaradás Szimmetriája

A modern fizika szemszögéből az energiamegmaradás törvénye mélyebb összefüggésben áll az időbeli szimmetriával, ahogy azt Emmy Noether híres tétele kimondja. A Noether-tétel szerint minden differenciálható fizikai hatáselvre létezik egy megmaradó mennyiség, amely a hatáselv egy folytonos szimmetriájának felel meg. Az energiamegmaradás esetében ez a szimmetria az időbeli eltolással szembeni invariancia. Ha a fizikai törvények nem változnak az időben, akkor az energia megmarad.

Az Energia Különböző Formái és Átalakulásaik

Az energia a természetben számos különböző formában létezik, és ezek egymásba alakulhatnak az energiamegmaradás törvényének megfelelően.

Mechanikai Energia: Kinetikus és Potenciális Energia

A mechanikai energia egy test mozgásával és helyzetével kapcsolatos energia. Két fő összetevője van: a kinetikus energia, amely a mozgásból származik, és a potenciális energia, amely a test helyzetéből vagy konfigurációjából adódik.

A $m$ tömegű, $v$ sebességgel mozgó test kinetikus energiája:

$$E_k = \frac{1}{2}mv^2$$

A $m$ tömegű, a gravitációs mezőben $h$ magasságban lévő test gravitációs potenciális energiája (a földfelszínhez képest):

$$E_p = mgh$$

Egy ideális rugó által tárolt rugalmas potenciális energia, amely $x$ távolsággal van megnyújtva vagy összenyomva ($k$ a rugóállandó):

$$E_{pr} = \frac{1}{2}kx^2$$

Amikor egy tárgy leesik, a potenciális energiája kinetikus energiává alakul, miközben a teljes mechanikai energia (ideális esetben, légellenállás nélkül) megmarad.

Hőenergia: A Részecskék Mozgásának Energiája

A hőenergia egy anyag atomjainak és molekuláinak véletlenszerű mozgásával kapcsolatos energia. Minél gyorsabban mozognak ezek a részecskék, annál nagyobb a hőmérséklete és a belső energiája az anyagnak. A hő átadódhat vezetéssel, áramlással és sugárzással, de a teljes energia egy zárt rendszerben megmarad.

Elektromágneses Energia: Fény és Elektromos Mezők Energiája

Az elektromágneses energia az elektromos és mágneses mezőkkel kapcsolatos energia. A fény, a rádióhullámok, a mikrohullámok, az infravörös és az ultraibolya sugárzás mind az elektromágneses energia formái. Az elektromágneses mezők energiát tárolhatnak, és ez az energia kölcsönhatásba léphet töltött részecskékkel.

Kémiai Energia: A Kötésekben Tárolt Energia

A kémiai energia az atomokat és molekulákat összetartó kémiai kötésekben tárolt energia. Kémiai reakciók során ezek a kötések felbomolhatnak és újak jöhetnek létre, miközben energia szabadul fel (exoterm reakciók) vagy nyelődik el (endoterm reakciók). Például az égés során a kémiai energia hő- és fényenergiává alakul, de a teljes energia megmarad.

Nukleáris Energia: Az Atommagban Tárolt Energia

A nukleáris energia az atommagban tárolt energia, amely az erős és gyenge kölcsönhatásokkal kapcsolatos. Nukleáris reakciók, mint például a maghasadás (atomerőművekben) és a magfúzió (a Napban), hatalmas mennyiségű energiát szabadíthatnak fel azáltal, hogy az atommagok tömege egy kis mértékben energiává alakul át (az $E=mc^2$ egyenlet szerint).

Példák az Energiamegmaradásra a Mindennapi Életben

Az energiamegmaradás törvénye számos mindennapi jelenség megértésének kulcsa.

Egy Hintázó Gyermek Energiája

Amikor egy gyermek hintázik, folyamatosan átalakul a potenciális és a kinetikus energia egymásba. A legmagasabb pontokon a kinetikus energia nulla, és a potenciális energia maximális. Az alsó ponton a potenciális energia (a referenciaszinthez képest) minimális, és a kinetikus energia maximális. Légellenállás és súrlódás nélkül a rendszer teljes mechanikai energiája állandó maradna.

Egy Villanykörte Működése

Egy hagyományos izzólámpában az elektromos energia hővé és fénnyé alakul át. Bár a cél a fény kibocsátása, jelentős mennyiségű energia hő formájában veszik el. Az energiamegmaradás törvénye szerint az elektromos energia mennyisége egyenlő a kibocsátott fényenergia és a keletkezett hőenergia összegével.

Egy Autó Mozgása

Egy autóban a benzin kémiai energiája először hővé alakul a motorban, majd ez a hőenergia mechanikai munkává alakul, amely a kerekeket hajtja. A folyamat során energia vész el súrlódás és légellenállás formájában, de a teljes energia (a benzin kémiai energiája) átalakul különböző formákba, és nem vész el.

Az Energiamegmaradás Törvényének Alkalmazásai a Tudományban és a Technikában

Az energiamegmaradás törvénye nem csupán egy elméleti elv, hanem számos tudományos és technikai alkalmazás alapját képezi.

Energiatermelés és -átalakítás

Az erőművekben az energia egyik formából (pl. fosszilis tüzelőanyagok kémiai energiája, víz mozgási energiája, napfény sugárzási energiája, szél kinetikus energiája) elektromos energiává alakul át. Az energiamegmaradás törvénye biztosítja, hogy az átalakítás során a teljes energia mennyisége megmaradjon, bár az átalakítás hatásfoka sosem lehet 100% a veszteségek (pl. hő formájában) miatt.

Gépészet és Mérnöki Tervezés

A gépek és szerkezetek tervezésénél elengedhetetlen az energiamegmaradás elvének figyelembevétele. Például egy hullámvasút tervezésénél a mérnökök kiszámítják a kocsi potenciális és kinetikus energiájának átalakulását, hogy biztosítsák a pálya biztonságos bejárását. A motorok és generátorok működése szintén az energia egyik formából a másikba való átalakításán alapul.

Fenntartható Energiaforrások

A megújuló energiaforrások, mint a napenergia, a szélenergia és a vízenergia, az energiamegmaradás elvén alapulnak abban az értelemben, hogy a Földre érkező vagy a természetben már meglévő energiát alakítják át hasznos formává anélkül, hogy kimerítenék az energiaforrást. A napkollektorok a nap sugárzási energiáját hővé alakítják, a napelemek pedig elektromos árammá. A szélturbinák a szél kinetikus energiáját alakítják át mechanikai, majd elektromos energiává. A vízerőművek a víz gravitációs potenciális energiáját alakítják át először kinetikussá, majd elektromossá.

Az Energiamegmaradás Törvényének Kiterjesztései és Korlátai

Bár az energiamegmaradás törvénye egyetemesnek tűnik, fontos megjegyezni, hogy bizonyos körülmények között a megfogalmazása finomodhat vagy kiterjesztésre szorul.

A Relativitáselmélet és a Tömeg-Energia Ekvivalencia

Einstein speciális relativitáselmélete megmutatta, hogy a tömeg és az energia valójában egyazon dolog két különböző megnyilvánulása, amelyeket az $E=mc^2$ egyenlet kapcsol össze, ahol $E$ az energia, $m$ a tömeg, és $c$ a fény sebessége vákuumban. Ez azt jelenti, hogy a tömeg is átalakulhat energiává, és fordítva. Ez különösen fontos a nukleáris reakciók és a kozmikus jelenségek leírásakor, ahol a tömeg jelentős mértékben alakulhat át energiává.

A Kvantummechanika és az Energia Meghatározatlansága

A kvantummechanikában a Heisenberg-féle határozatlansági elv kimondja, hogy bizonyos fizikai mennyiségek, mint például a helyzet és a lendület, vagy az energia és az idő, nem mérhetők meg tetszőleges pontossággal egyszerre. Az energia és az idő közötti határozatlansági reláció ($\Delta E \Delta t \ge \frac{\hbar}{2}$) azt jelenti, hogy rövid időtartamokra az energia nem feltétlenül marad pontosan meg, ami lehetővé teszi például a virtuális részecskék megjelenését és eltűnését.

Nyitott Rendszerek és Energiaáramlás

A valódi rendszerek többsége nem teljesen zárt; kölcsönhatásban állnak a környezetükkel, és energiát cserélnek vele. Nyitott rendszerek esetében a rendszer energiája megváltozhat a környezetével való energiaáramlás következtében. Azonban a rendszer és a környezet együttes energiája továbbra is megmarad (ha a teljes rendszer tekinthető zártnak).

Összefoglalás: Az Energiamegmaradás Törvényének Jelentősége

Az energiamegmaradás törvénye a fizika egyik sarokköve, amely alapvető korlátokat szab a természeti jelenségeknek és a technológiai folyamatoknak. Megértése elengedhetetlen a tudományos kutatásban, a mérnöki tervezésben és a fenntartható jövő megteremtésében. Bár a relativitáselmélet és a kvantummechanika árnyalják a képét, az alapelv – hogy az energia nem vész el, csak átalakul – továbbra is érvényes marad a megfigyelhető univerzumban.

További Kutatási Lehetőségek az Energiamegmaradás Területén

Bár az energiamegmaradás törvénye jól megalapozott, a kutatás továbbra is zajlik az energia tárolásának hatékonyabb módjai, az energiaveszteségek minimalizálása és az új, fenntartható energiaforrások feltárása terén. A kvantumos energiatárolás, az új anyagok fejlesztése az energiaátalakításhoz és a fúziós energia kutatása mind olyan területek, ahol az energiamegmaradás elvének mélyebb megértése és kreatív alkalmazása kulcsfontosságú lehet a jövő számára.

Az Energiamegmaradás Törvényének Oktatása és Népszerűsítése

Az energiamegmaradás törvényének megértése nem csupán a tudósok és mérnökök számára fontos. A társadalom szélesebb körének ismerete segíthet a környezettudatos gondolkodás és a fenntartható életmód kialakításában. Az oktatásnak és a tudományos ismeretterjesztésnek kiemelt szerepe van abban, hogy az emberek megértsék az energia fogalmát, annak különböző formáit és az átalakítások során fellépő korlátokat.

Gyakorlati Feladatok és Példák az Energiamegmaradás Illusztrálására

A tantermekben és otthon is számos egyszerű kísérlettel és feladattal lehet szemléltetni az energiamegmaradás elvét. Egy leeső labda mozgásának elemzése, egy rugó kilengésének vizsgálata vagy egy egyszerű elektromos áramkör működésének megértése mind-mind segíthet a diákoknak és az érdeklődőknek abban, hogy kézzelfogható módon tapasztalják meg az energia átalakulásait és megmaradását.

Következtetés: Az Energiamegmaradás Törvényének Időtlen Érvényessége

Végső soron az energiamegmaradás törvénye egy olyan alapelv, amely túlmutat a pillanatnyi tudományos ismereteinken. Ez egy olyan univerzális igazság, amely a fizikai világ működésének mélyére hatol, és amely nélkül a természet számos jelenségét nem érthetnénk meg. Ahogy haladunk előre a tudomány és a technológia fejlődésében, az energiamegmaradás törvénye továbbra is iránytűként szolgál számunkra az új felfedezések és innovációk felé vezető úton.

Reméljük, hogy ez az

Energiamegmaradas Torvenye Fogalom

Az Energiamegmaradás Törvénye: A Természet Alapvető Elve

Az energiamegmaradás törvénye a fizika egyik legfontosabb és legalapvetőbb elve, amely kimondja, hogy egy zárt rendszer teljes energiája időben állandó marad. Ez azt jelenti, hogy az energia nem keletkezhet a semmiből és nem veszhet el, csupán egyik formájából átalakulhat egy másikba. Ez a törvény áthatja a természettudományok szinte minden területét, a mechanikától a termodinamikán át az elektromágnesességig és a részecskefizikáig. Célunk, hogy ebben az átfogó cikkben részletesen feltárjuk az energiamegmaradás törvényének fogalmát, történeti hátterét, matematikai megfogalmazását, különböző megnyilvánulásait és gyakorlati alkalmazásait, ezzel biztosítva a téma lehető legmélyebb megértését.

Az Energiamegmaradás Törvényének Fogalma és Alapelvei

Az energiamegmaradás törvényének lényege, hogy a világegyetem teljes energiaállománya konstans. Bármilyen folyamat is zajlik, az energia összértéke nem változik. Amikor egy rendszer látszólag energiát veszít, az valójában egy másik formában vagy egy másik rendszerben jelenik meg. Például, amikor egy tárgy leesik, a potenciális energia mozgási energiává alakul át. Amikor egy égő gyufa fényt és hőt bocsát ki, a kémiai energia hő- és sugárzási energiává alakul. Ezek a példák jól illusztrálják az energia átalakulásának folyamatát, miközben a teljes energia mennyisége megmarad.

A Zárt Rendszer Koncepciója az Energiamegmaradásban

Az energiamegmaradás törvényének pontos megértéséhez elengedhetetlen a zárt rendszer fogalmának tisztázása. Egy zárt rendszer olyan rendszer, amely nem cserél energiát a környezetével. A valóságban tökéletesen zárt rendszerek nem léteznek, de sok fizikai modellünkben idealizált zárt rendszereket vizsgálunk a jelenségek megértéséhez. Ha egy rendszer nincs elszigetelve a környezetétől, akkor energia áramolhat be vagy ki belőle, és ebben az esetben a rendszer energiája megváltozhat. Az energiamegmaradás törvénye azonban a teljes, izolált univerzumra mindenképpen érvényesnek tekinthető.

Az Energia Különböző Formái és Átalakulásuk

Az energia számos különböző formában létezhet, és ezek egymásba alakulhatnak. Néhány alapvető energiaforma a következő:

• Mechanikai energia: amely magában foglalja a mozgási energiát (egy test mozgásából származó energia) és a potenciális energiát (egy test helyzetéből vagy állapotából származó energia).
• Hőenergia (Termikus energia): amely az atomok és molekulák véletlenszerű mozgásával kapcsolatos energia.
• Elektromágneses energia: amely elektromos és mágneses mezőkkel kapcsolatos energia, beleértve a fényt és más elektromágneses sugárzásokat.

• Kémiai energia: amely az atomok közötti kémiai kötésekben tárolt energia.
• Nukleáris energia: amely az atommagban tárolt energia.

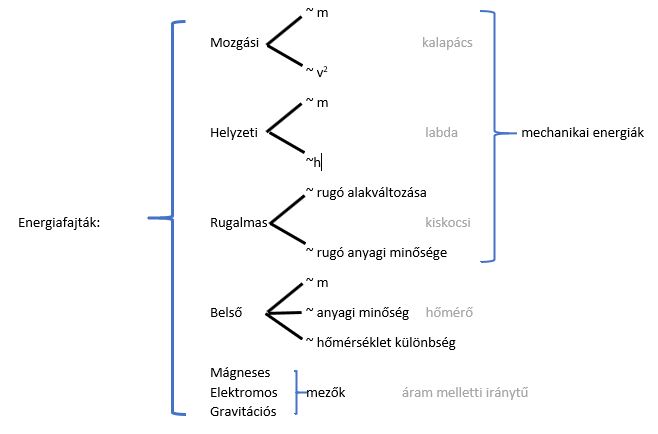
Az energiamegmaradás törvénye azt mondja ki, hogy egy zárt rendszerben ezen energiaformák összege állandó, bár az egyes formák egymásba alakulhatnak. Például egy vízerőműben a víz potenciális energiája mozgási energiává alakul, ami aztán elektromos energiává alakul a generátorokban.

Az Energiamegmaradás Törvényének Történeti Áttekintése

Az energiamegmaradás törvényének felismerése egy hosszú és kanyargós tudományos folyamat eredménye volt, amelyben számos tudós járult hozzá különböző meglátásaival és kísérleteivel.

A Korai Elképzelések és a Mechanikai Ekvivalens Keresése

A 17. és 18. században a tudósok, mint például Gottfried Wilhelm Leibniz, már felvetették a *vis viva* (élő erő), azaz a $mv^2$ mennyiség megmaradásának gondolatát bizonyos mechanikai kölcsönhatásokban. Bár ez nem azonos a modern értelemben vett energiával, fontos előfutára volt az energiamegmaradás elvének. A 19. század elején kezdett elterjedni az a felismerés, hogy a hő is egyfajta energia, és kapcsolatban áll a mechanikai munkával. Benjamin Thompson (gróf Rumford) híres kísérletei ágyúfúrás közben megfigyelt hőtermeléssel megkérdőjelezték a hő korábbi, anyagként való értelmezését (a kalorikus elméletet).

A Termodinamika Első Főtételének Megszületése

Az energiamegmaradás törvényének egyik legfontosabb mérföldköve a termodinamika első főtételének megfogalmazása volt a 19. század közepén. Ezt a tételt Hermann von Helmholtz, Julius Robert Mayer és James Prescott Joule egymástól függetlenül fogalmazták meg különböző formákban. Joule kísérletei különösen jelentősek voltak, amelyekkel sikerült meghatároznia a mechanikai munka és a hő közötti ekvivalenciát (a hő mechanikai egyenértékét). Mayer orvosi megfigyeléseiből kiindulva jutott el az energia megmaradásának gondolatához, míg Helmholtz átfogóbb elméleti keretet dolgozott ki. A termodinamika első főtétele formálisan kimondja, hogy egy rendszer belső energiájának megváltozása egyenlő a rendszerrel közölt hő és a rendszeren végzett munka összegével: $\Delta U = Q – W$. Ez az egyenlet az energiamegmaradás törvényének termodinamikai megfogalmazása.

Az Energiamegmaradás Általános Elvvé Válása

A termodinamika fejlődésével párhuzamosan az energiamegmaradás elve egyre általánosabb elfogadottságra tett szert a fizika más területein is. Az elektromágnesesség elméletének kidolgozása során kiderült, hogy az elektromágneses mező is energiát hordoz, és az energia megmarad az elektromágneses kölcsönhatások során is. Albert Einstein speciális relativitáselmélete tovább tágította az energiamegmaradás fogalmát azáltal, hogy megmutatta az energia és a tömeg ekvivalenciáját ($E=mc^2$), ami azt jelenti, hogy a tömeg is az energia egyik formája lehet, és átalakulhat energiává, illetve fordítva. A modern fizika minden területén, a klasszikus mechanikától a kvantummechanikán át a kozmológiáig, az energiamegmaradás törvénye alapvető axiómának számít.

Az Energiamegmaradás Törvényének Matematikai Megfogalmazása

Az energiamegmaradás törvénye matematikai formában is kifejezhető, ami lehetővé teszi a fizikai rendszerek energiaegyenségének kvantitatív leírását.

A Mechanikai Energia Megmaradása Konzervatív Erőterekben

Egy olyan rendszerben, ahol csak konzervatív erők hatnak (mint például a gravitációs erő vagy az ideális rugóerő), a mechanikai energia megmarad. A mechanikai energia a mozgási energia ($K$) és a potenciális energia ($U$) összege: $E_{mech} = K + U$. Az energiamegmaradás ebben az esetben azt jelenti, hogy a rendszer mechanikai energiája időben állandó: $\frac{dE_{mech}}{dt} = 0$, vagyis $K_1 + U_1 = K_2 + U_2$, ahol az 1-es és 2-es indexek a rendszer két különböző állapotát jelölik.

A Termodinamika Első Főtételének Matematikai Formája

Mint korábban említettük, a termodinamika első főtétele az energiamegmaradás törvényének termodinamikai megfogalmazása. Egy zárt rendszerben a belső energia ($U$) megváltozása ($\Delta U$) egyenlő a rendszerrel közölt hő ($Q$) és a rendszeren végzett munka ($W$) különbségével: $\Delta U = Q – W$. Differenciális formában ez így írható: $dU = \delta Q – \delta W$, ahol a $\delta$ jelölés azt hangsúlyozza, hogy a hő és a munka nem állapotfüggvények, hanem folyamatfüggvények.

A Noether-tétel Kapcsolata az Energiamegmaradással

A modern fizika egyik mélyreható eredménye a Noether-tétel, amely kimondja, hogy minden differenciálható szimmetriához egy megmaradó mennyiség tartozik. Az időbeli eltolási szimmetria (a fizikai törvények időben változatlanok) éppen az energia megmaradásához vezet. Ez a tétel rávilágít az energiamegmaradás törvényének alapvető jellegére a fizikai törvények szimmetriáival való mély kapcsolatán keresztül.

Különböző Energiafajták és az Energiamegmaradás

Az energiamegmaradás törvénye érvényesül az energia minden formájának átalakulása során.

Mechanikai Energia: Mozgási és Potenciális Energia

A mechanikai energia, mint említettük, a mozgási és potenciális energia összege. Egy ideális inga mozgása jó példa a mechanikai energia megmaradására (ha elhanyagoljuk a súrlódást). A legmagasabb ponton az ingának maximális potenciális energiája és nulla mozgási energiája van, míg a legalacsonyabb ponton a potenciális energia minimális (általában nullának vesszük), és a mozgási energia maximális. A köztes pontokon az energia folyamatosan átalakul a két forma között, de az összegük állandó marad.

Termikus Energia és az Energiamegmaradás

A termikus energia a rendszer belső energiájának része, amely a mikroszkopikus részecskék (atomok, molekulák) véletlenszerű mozgásával kapcsolatos. Amikor mechanikai munka hővé alakul (például súrlódás révén), vagy amikor hő hatására egy test munkát végez (például egy gáz tágulása egy hengerben), az energiamegmaradás törvénye továbbra is érvényesül. A termodinamika első főtétele éppen ezt az energiaegyenséget írja le termodinamikai rendszerekben.

Elektromágneses Energia és az Energiamegmaradás

Az elektromágneses mező energiát tárolhat és szállíthat. Például egy kondenzátor elektromos mezőben tárol energiát, míg egy induktor mágneses mezőben. Amikor egy elektromágneses hullám (például a fény) terjed, az elektromos és mágneses mezők energiát szállítanak a térben. Az energiamegmaradás itt azt jelenti, hogy az elektromágneses mező energiájának megváltozása egyenlő a rendszerrel végzett munkával és a hőcserével.

Kémiai Energia és az Energiamegmaradás

A kémiai energia a molekulákban lévő kémiai kötésekben tárolt potenciális energia. Kémiai reakciók során ezek a kötések felbomolhatnak és újak jöhetnek létre, ami energia felszabadulásával (exoterm reakciók) vagy energiafelvétellel (endoterm reakciók) járhat. Az energiamegmaradás törvénye azt biztosítja, hogy a reakcióban részt vevő anyagok energiájának és a felszabaduló vagy elnyelt energiának az összege állandó marad.

Nukleáris Energia és az Energiamegmaradás

A nukleáris energia az atommagban tárolt energia, amely a nukleonok (protonok és neutronok) közötti erős és gyenge kölcsönhatásokkal kapcsolatos. Nukleáris reakciók, mint a maghasadás (pl. atomerőművekben) vagy a magfúzió (pl. a Napban), hatalmas mennyiségű energia felszabadulásával járhatnak. Ebben az esetben az Einstein-féle $E=mc^2$ egyenlet is fontos szerepet játszik, mivel a tömeg egy része energiává alakul. Az energiamegmaradás itt a teljes energia (beleértve a tömegből származó energiát is) megmaradását jelenti.

Az Energiamegmaradás Törvényének Gyakorlati Alkalmazásai

Az energiamegmaradás törvénye nem csupán egy elméleti elv, hanem számos technológiai és mérnöki alkalmazás alapját képezi.

Energiatermelés és -átalakítás

Szinte minden energiatermelő technológia az energia egyik formájának egy másikba való átalakításán alapul, miközben az energiamegmaradás törvényét tiszteletben tartja. Például:

• Hőerőművek: Vegyi energia (pl. szénben, gázban) hőenergiává alakul, ami gőzt termel, ami turbinákat hajt meg, amelyek elektromos energiát generálnak.
• Vízerőművek: A víz potenciális energiája mozgási energiává alakul, ami turbinákat hajt meg, elektromos energiát termelve.
• Szélenergia: A szél mozgási energiája forgatja a szélturbinákat, amelyek elektromos energiát termelnek.
• Naperőművek: A nap sugárzási energiája közvetlenül (fotovoltaikus panelekben) vagy közvetetten (hőerőművekben) elektromos energiává alakul.

Mindegyik esetben az energia egyik formája alakul át egy másikba, a teljes energia mennyisége pedig megmarad (bár egy része hasznos munkavégzés helyett gyakran hő formájában “veszteségként” jelentkezik).

Közlekedés

A közlekedési eszközök működése is az energiamegmaradás törvényén alapul. Egy autóban a benzin kémiai energiája hővé és mozgási energiává alakul. Egy elektromos autóban az akkumulátorban tárolt kémiai energia elektromos energiává alakul, ami a motort hajtja meg, mozg

Energiamegmaradas Torvenye Definicio

Az Energiamegmaradás Törvénye: A Világegyetem Alapvető Elve

Az energiamegmaradás törvénye a fizika egyik legfontosabb és legalapvetőbb elve, amely kimondja, hogy egy izolált rendszer teljes energiája időben állandó marad. Ez azt jelenti, hogy az energia nem keletkezhet a semmiből és nem veszhet el, csupán egyik formájából átalakulhat egy másikba. Ez a tétel áthatja a természettudományok szinte minden területét, a klasszikus mechanikától a termodinamikán át az elektromágnesességig és a részecskefizikáig. Az energia megmaradása nem csupán egy elméleti konstrukció, hanem számtalan kísérleti megfigyelés és gyakorlati alkalmazás támasztja alá.

Az Energiamegmaradás Törvényének Definíciója és Mélyebb Értelmezése

A legegyszerűbb megfogalmazás szerint az energiamegmaradás törvénye azt állítja, hogy egy zárt rendszerben az energia mennyisége nem változik. Fontos kiemelni a “zárt rendszer” fogalmát. Egy zárt rendszer olyan rendszer, amely nem cserél energiát a környezetével. A valóságban tökéletesen zárt rendszerek ritkán léteznek, de sok esetben a vizsgált rendszer olyan mértékben van elszigetelve a környezetétől, hogy az energiaáramlás elhanyagolható. Ha egy rendszer nem zárt, akkor az energiája megváltozhat a környezetével való energiaátadás következtében (pl. hő formájában végzett munka).

Az energia egy absztrakt fogalom, amely a munka végzésének képességét vagy a hőátadás lehetőségét írja le. Különböző formákban jelenhet meg, mint például a kinetikus energia (mozgási energia), a potenciális energia (helyzeti energia), a hőenergia (a részecskék mozgásából származó energia), az elektromágneses energia (elektromos és mágneses mezőkhöz kapcsolódó energia), a kémiai energia (a kémiai kötésekben tárolt energia) és a nukleáris energia (az atommagban tárolt energia). Az energiamegmaradás törvénye azt mondja ki, hogy egy zárt rendszerben ezen energiafajták összessége állandó, bár az egyik forma átalakulhat egy másikba.

Az Energiamegmaradás Történeti Áttekintése

Az energiamegmaradás gondolata nem egyetlen pillanatban fogalmazódott meg, hanem tudósok és filozófusok évszázados munkájának eredménye. Már a korai gondolkodók is felismerték, hogy valamilyen állandóság létezik a természeti jelenségek mögött. A 17. században például Gottfried Wilhelm Leibniz bevezette a “vis viva” (élő erő) fogalmát, amely a mai kinetikus energia fogalmának elődje volt ($mv^2$). Leibniz úgy vélte, hogy a természetben a “vis viva” megmarad.

A 19. század elején olyan tudósok, mint Julius Robert Mayer, James Prescott Joule és Hermann von Helmholtz, egymástól függetlenül jutottak arra a felismerésre, hogy a hő és a mechanikai munka ekvivalens formái az energiának, és hogy az energia összességében megmarad. Joule kísérletei, amelyekben mechanikai munkával hőt fejlesztett, kulcsfontosságúak voltak az energiamegmaradás elvének kísérleti alátámasztásában. Helmholtz pedig 1847-ben megjelent “Über die Erhaltung der Kraft” (Az erő megmaradásáról) című munkájában fogalmazta meg az energiamegmaradás általános elvét.

A Termodinamika Első Főtétele és az Energiamegmaradás

A termodinamika első főtétele az energiamegmaradás törvényének egyik legfontosabb megfogalmazása a termodinamikai rendszerekre. Kimondja, hogy egy zárt rendszer belső energiájának ($U$) megváltozása egyenlő a rendszerrel közölt hő ($Q$) és a rendszeren végzett munka ($W$) összegével: $$\Delta U = Q + W$$. Ez az egyenlet azt fejezi ki, hogy az energia nem vész el és nem keletkezik, csupán a rendszer és a környezete között cserélődhet hő vagy munka formájában, ami megváltoztatja a rendszer belső energiáját.

Az Energiamegmaradás Matematikai Megfogalmazásai

Az energiamegmaradás törvényét különböző matematikai formákban is ki lehet fejezni, attól függően, hogy milyen rendszert vizsgálunk. A klasszikus mechanikában egy konzervatív erőterekben mozgó részecskerendszer teljes energiája ($E$), amely a kinetikus energia ($K$) és a potenciális energia ($U_{pot}$) összege, időben állandó: $$E = K + U_{pot} = \text{állandó}$$. Ha nem konzervatív erők (pl. súrlódás) is jelen vannak, akkor a mechanikai energia nem marad meg, hanem más energiaformákká (pl. hővé) alakul át, de a rendszer és a környezet teljes energiája továbbra is megmarad.

A kvantummechanikában az energiamegmaradás szintén alapvető fontosságú. A Schrödinger-egyenlet időfüggő formája írja le egy kvantumrendszer állapotának időbeli fejlődését, és ha a Hamilton-operátor (amely a rendszer energiáját reprezentálja) nem függ explicit módon az időtől, akkor a rendszer energiája megmarad.

Az Energia Különböző Formái és Azok Átalakulásai

Ahogy korábban említettük, az energia számos formában létezhet, és az energiamegmaradás törvénye lehetővé teszi, hogy megértsük, hogyan alakul át egyik forma a másikba. Nézzünk meg néhány példát:

• Mechanikai energia: Kinetikus energia (mozgás) és potenciális energia (helyzet vagy konfiguráció). Például egy leejtett labda potenciális energiája fokozatosan kinetikus energiává alakul át, miközben esik. A becsapódáskor ez a kinetikus energia részben hővé és hanggá alakul.
• Hőenergia: Az atomok és molekulák véletlenszerű mozgásából származik. Amikor egy testet felmelegítünk, a részecskéinek mozgási energiája nő. A hőenergia átadható egyik testről a másikra hővezetés, hőáramlás vagy hősugárzás útján.

• Elektromágneses energia: Az elektromos és mágneses mezőkhöz kapcsolódik. Ide tartozik a fény, a rádióhullámok, a röntgensugarak stb. Egy elektromos motor az elektromos energiát mechanikai energiává alakítja, míg egy generátor a mechanikai energiát elektromos energiává.

• Kémiai energia: A molekulákban lévő kémiai kötésekben tárolódik. Kémiai reakciók során ez az energia felszabadulhat (exoterm reakciók) vagy elnyelődhet (endoterm reakciók). Például az égés során a kémiai energia hővé és fényé alakul.
• Nukleáris energia: Az atommagban tárolt energia. Atommagreakciók (pl. maghasadás, magfúzió) során hatalmas mennyiségű energia szabadulhat fel.

Az energiamegmaradás törvénye azt biztosítja, hogy bár az energia formája megváltozhat, a teljes mennyisége egy zárt rendszerben mindig ugyanaz marad.

Gyakorlati Alkalmazások: Hogyan Használjuk Ki az Energiamegmaradás Elvét?

Az energiamegmaradás törvényének megértése és alkalmazása elengedhetetlen a tudomány és a technológia számos területén:

• Energiatermelés: A különböző erőművek (hőerőművek, vízerőművek, szélerőművek, atomerőművek) mind az energia egyik formájának egy másikba történő átalakításán alapulnak. Például egy vízerőmű a víz potenciális energiáját alakítja át először kinetikus energiává, majd elektromos energiává.
• Közlekedés: A járművek (autók, repülők, vonatok) működése szintén az energiaátalakításon alapul. Egy belső égésű motor a kémiai energiát alakítja át mechanikai munkává.
• Építészet és épületgépészet: Az energiahatékony épületek tervezése és a fűtési, szellőztetési rendszerek optimalizálása az energiamegmaradás elvén alapul. A hőszigetelés például csökkenti a hőveszteséget, így kevesebb energiára van szükség a fűtéshez.
• Kémia: A kémiai reakciók energiaváltozásainak megértése és előrejelzése a termodinamika, és ezen belül az energiamegmaradás alapvető fontosságú.

• Biológia: Az élőlények anyagcseréje és működése energiaátalakítási folyamatok sorozata. A táplálékban tárolt kémiai energia alakul át a sejtek által hasznosítható energiává.

Az Energiamegmaradás és a Perpetuum Mobile

Az energiamegmaradás törvénye közvetlenül cáfolja a perpetuum mobile létezését. A perpetuum mobile egy olyan hipotetikus gép, amely külső energiaforrás nélkül képes folyamatosan munkát végezni (elsőfajú perpetuum mobile) vagy a környezetéből hőt elvonva azt teljes egészében munkává alakítani (másodfajú perpetuum mobile). Az energiamegmaradás kimondja, hogy energia nem teremthető a semmiből, ezért egy elsőfajú perpetuum mobile nem létezhet. A termodinamika második főtétele pedig kizárja a másodfajú perpetuum mobile lehetőségét is.

Az Energiamegmaradás Kiterjesztése: A Tömeg-Energia Ekvivalencia

Albert Einstein speciális relativitáselmélete forradalmasította az energiamegmaradás fogalmát a híres $E=mc^2$ egyenletével. Ez az egyenlet kifejezi a tömeg és az energia ekvivalenciáját, ami azt jelenti, hogy a tömeg az energia egyik formája, és az energia tömeggé alakulhat, és fordítva. Ez különösen fontos a nukleáris reakciókban, ahol mérhető tömegveszteség tapasztalható, amely az energiamegmaradás értelmében energiává alakul.

A Megújuló Energiaforrások és az Energiamegmaradás

A megújuló energiaforrások (napenergia, szélenergia, vízenergia, geotermikus energia, biomassza) mind olyan természeti folyamatokból származnak, amelyek végső soron a Nap energiájára vagy a Föld belső hőjére vezethetők vissza. Ezek az energiaforrások az energiamegmaradás elvét követve alakítják át a rendelkezésre álló energiát hasznos formákká anélkül, hogy kimerítenék az energiaforrást a szó hagyományos értelmében.

Összefoglalás: Az Energiamegmaradás Törvényének Fontossága

Az energiamegmaradás törvénye a fizika egyik sarokköve, amely nélkül a természeti jelenségek megértése és a technológiai fejlesztések elképzelhetetlenek lennének. Ez az alapelv nem csupán leírja a világ működését, hanem korlátokat is szab a lehetséges folyamatoknak (például a perpetuum mobile lehetetlensége). Az energia megmaradása biztosítja a kozmosz bizonyos szintű állandóságát és lehetővé teszi számunkra, hogy megértsük az energia különböző formái közötti kapcsolatokat és átalakulásokat.

Reméljük, hogy ez az átfogó cikk segített megérteni az energiamegmaradás törvényének lényegét és jelentőségét. Ha további kérdései vannak, ne habozzon feltenni őket!