Energiamegmaradas Torvenye Pelda

Az Energia-megmaradás Törvénye: A Világegyetem Alapvető Elve

Az energia-megmaradás törvénye a fizika egyik legfontosabb és legátfogóbb alapelve. Kimondja, hogy egy zárt rendszer teljes energiája időben állandó marad. Ez azt jelenti, hogy az energia nem teremthető és nem pusztítható el, csupán egyik formájából a másikba alakulhat át. Ez a látszólag egyszerű kijelentés mélyreható következményekkel jár a természeti jelenségek megértésére és a technológiai fejlesztésekre nézve. Cikkünkben részletesen feltárjuk az energia-megmaradás törvényének jelentését, különböző megjelenési formáit, és számos példán keresztül szemléltetjük alkalmazását a tudomány és a mindennapi élet különböző területein. Célunk, hogy egy átfogó és érthető képet nyújtsunk erről a fundamentális természeti törvényről, amely áthatja a minket körülvevő világ minden aspektusát.

Az Energia Fogalmának Meghatározása és Különböző Formái

Ahhoz, hogy megértsük az energia-megmaradás törvényét, először tisztáznunk kell magának az energia fogalmát. Az energia egy rendszer azon képessége, hogy munkát végezzen. Bár gyakran nehéz közvetlenül érzékelni, az energia jelenléte a különböző folyamatokban nyilvánvalóvá válik. Az energia számos különböző formában létezhet, amelyek mindegyike fontos szerepet játszik a természeti jelenségekben és a technológiai alkalmazásokban. Nézzük meg a legfontosabb energiaformákat:

Mechanikai Energia: Mozgás és Pozíció Potenciálja

A mechanikai energia egy test mozgásából (kinetikus energia) vagy a rá ható erőtérben elfoglalt helyzetéből (potenciális energia) származik. A kinetikus energia a mozgó testekkel kapcsolatos energia, amely a tömegüktől és a sebességük négyzeteivel arányos: $E_k = \frac{1}{2}mv^2$. Például egy guruló labdának, egy repülő repülőgépnek vagy egy forgó keréknek kinetikus energiája van. A potenciális energia egy test helyzetéből adódó energia egy erőterben. A leggyakoribb példa a gravitációs potenciális energia, amely egy test magasságától függ egy gravitációs mezőben: $E_p = mgh$, ahol $m$ a tömeg, $g$ a gravitációs gyorsulás, és $h$ a magasság egy referencia szinthez képest. Egy felemelt kőnek vagy egy megfeszített rugónak potenciális energiája van.

Hőenergia: A Részecskék Mozgásának Következménye

A hőenergia, más néven termikus energia, egy anyag atomjainak és molekuláinak véletlenszerű mozgásával kapcsolatos energia. Minél gyorsabban mozognak ezek a részecskék, annál nagyobb az anyag hőenergiája és annál magasabb a hőmérséklete. A hőenergia átadódhat egyik testről a másikra hő formájában, amelynek három fő módja van: hővezetés (kondukció), hőáramlás (konvekció) és hősugárzás (radiáció). A hőenergia alapvető szerepet játszik a termodinamikai folyamatokban és a mindennapi jelenségekben, mint például a víz forrása vagy a testünk melegen tartása.

Elektromágneses Energia: A Töltött Részecskék Kölcsönhatása

Az elektromágneses energia az elektromos és mágneses mezőkkel kapcsolatos energia. Ide tartozik a fény, a rádióhullámok, a mikrohullámok, az infravörös sugárzás, az ultraibolya sugárzás, a röntgensugarak és a gammasugarak. Ezek mind elektromágneses hullámok, amelyek energiát szállítanak. Az elektromos mezők töltött részecskék között hatnak, míg a mágneses mezők mozgó töltések (azaz áram) vagy mágneses dipólusok körül jönnek létre. Az elektromágneses energia nélkülözhetetlen a modern technológiában, az energiatermeléstől a kommunikációig.

Kémiai Energia: A Kötésekben Tárolt Potenciál

A kémiai energia az atomokat és molekulákat összetartó kémiai kötésekben tárolt potenciális energia. Ez az energia szabadul fel kémiai reakciók során, amikor a kötések átrendeződnek. Például a fa égésekor a fa molekuláiban tárolt kémiai energia hővé és fénnyé alakul át. Az élelmiszerekben tárolt kémiai energia pedig a szervezetünk számára biztosítja a működéshez szükséges energiát. A fosszilis tüzelőanyagok, mint a kőolaj, a földgáz és a szén, szintén jelentős mennyiségű kémiai energiát tárolnak.

Nukleáris Energia: Az Atommag Erejének Kiaknázása

A nukleáris energia az atommagban tárolt energia. Ez az energia felszabadulhat nukleáris reakciók során, mint például a maghasadás (fisszió), amikor egy nehéz atommag kisebb magokra bomlik, vagy a magfúzió (fúzió), amikor könnyű atommagok egyesülnek egy nehezebbé. A nukleáris energia hatalmas mennyiségű energiát képes felszabadítani, amit atomerőművekben villamos energia termelésére használnak, de atombombákban is alkalmaznak.

Az Energia-megmaradás Törvényének Formális Megfogalmazása

Az energia-megmaradás törvénye matematikailag is megfogalmazható. Egy zárt rendszerben a teljes energia ($E_{total}$) időben állandó:

$$\frac{dE_{total}}{dt} = 0$$

Ez azt jelenti, hogy ha egy rendszerben különböző energiaformák alakulnak át egymásba, a rendszer teljes energiája nem változik. Ha a rendszer nem zárt, azaz energia cserélődik a környezetével, akkor a rendszer energiájának megváltozása megegyezik a környezettel kicserélt energiával (munkavégzés vagy hőátadás formájában).

Történelmi Háttér: Az Energia-megmaradás Elvének Fejlődése

Az energia-megmaradás elvének felismerése egy hosszú és összetett folyamat volt a tudomány történetében. Számos tudós járult hozzá a koncepció kialakulásához különböző területeken végzett kísérleteikkel és elméleti munkájukkal.

A Korai Elképzelések és a Mechanikai Világnézet

A 17. és 18. században a tudósok, mint például Gottfried Wilhelm Leibniz, már felvetették a vis viva (élő erő) fogalmát, amely a mai kinetikus energiához hasonlít. Leibniz úgy vélte, hogy a vis viva megmarad a mechanikai kölcsönhatások során. Bár ez nem volt a teljes energia-megmaradás elve, fontos lépés volt a felé.

A Hő és a Munka Ekvivalenciájának Felfedezése

A 19. század elején olyan tudósok, mint Julius Robert Mayer, James Prescott Joule és Hermann von Helmholtz, kísérletekkel és elméleti megfontolásokkal kimutatták a hő és a munka közötti ekvivalenciát. Joule híres kísérleteivel bebizonyította, hogy a mechanikai munka hővé alakítható, és meghatározta a mechanikai munka és a hő egysége közötti átszámítási tényezőt (Joule-állandó). Mayer orvosi megfigyelései alapján jutott arra a következtetésre, hogy a hő és a munka különböző formái ugyanannak a dolognak, az energiának. Helmholtz pedig egy átfogó matematikai keretet adott az energia-megmaradás elvének.

Az Általános Elv Megszületése

Az 1840-es évekre az energia-megmaradás törvénye általánosan elfogadottá vált a tudományos közösségben, kiterjesztve a mechanikai, termikus, elektromos és kémiai jelenségekre is. Ez az elv alapvetővé vált a fizika és más természettudományok számára, és a mai napig is megkérdőjelezhetetlen érvényességgel bír.

Példák az Energia-megmaradás Törvényének Alkalmazására

Az energia-megmaradás törvénye számos természeti jelenség és technológiai alkalmazás megértésének kulcsa. Nézzünk meg néhány konkrét példát:

Mechanikai Rendszerek: A Hullámvasút Példája

Egy hullámvasút kocsija a pálya tetejére felhúzva potenciális energiával rendelkezik. Amikor a kocsi elindul lefelé, ez a potenciális energia fokozatosan kinetikus energiává alakul át, ami a kocsi sebességének növekedésében nyilvánul meg. A pálya alján a potenciális energia minimális, míg a kinetikus energia maximális. A felfelé ívelő szakaszokon a kinetikus energia ismét potenciális energiává alakul át. Ha nem lenne súrlódás és légellenállás, a kocsi folyamatosan ugyanarra a magasságra jutna vissza. A valóságban azonban a mechanikai energia egy része hővé alakul a súrlódás miatt, ezért a kocsi egyre alacsonyabbra jut a következő emelkedéseknél.

Termodinamikai Rendszerek: A Hőerőmű Működése

Egy hőerőműben valamilyen üzemanyag (például szén, földgáz vagy nukleáris anyag) elégetésével hőenergiát termelnek. Ez a hőenergia vizet forral fel, amely gőzt hoz létre. A nagynyomású gőz turbinákat hajt meg, amelyek mechanikai munkát végeznek. A turbinákhoz kapcsolt generátorok ezt a mechanikai munkát elektromos energiává alakítják át. Az energia-megmaradás törvénye itt abban nyilvánul meg, hogy az üzemanyagban tárolt kémiai vagy nukleáris energia végső soron elektromos energiává alakul át, miközben más energiaformák (például hőveszteség) is keletkeznek. A teljes energia mennyisége a folyamat során megmarad.

Elektromágneses Rendszerek: Az Elektromos Generátor

Egy elektromos generátor mechanikai energiát alakít át elektromos energiává. Például egy forgó mágnes egy tekercs közelében változó mágneses teret hoz létre, ami elektromos áramot indukál a tekercsben (Faraday-féle indukció). Az energia-megmaradás törvénye szerint a mechanikai munkával bevitt energia (a mágnes forgatása) az elektromos áram energiájává alakul át. A veszteségek (például a tekercs ellenállásából származó hő) szintén figyelembe veendők az energia-mérlegben.

Kémiai Reakciók: Az Égés Folyamata

A fa égése egy kémiai reakció, amely során a fa molekuláiban tárolt kémiai energia hővé és fénnyé alakul át. A reakció során a fa és az oxigén molekulái átrendeződnek, új molekulákat (például szén-dioxidot és vizet) hozva létre, miközben energia szabadul fel. Az energia-megmaradás törvénye itt azt jelenti, hogy a kiindulási anyagok kémiai energiájának és a felszabaduló hő- és fényenergiának az összege megegyezik a termékek kémiai energiájával (ami ebben az esetben alacsonyabb, mivel energia szabadult fel) plusz a környezetbe távozó bármilyen más energiával.

Nukleáris Reakciók: A Nap Működése

A Nap energiájának forrása a magfúzió, amelynek során a Nap magjában lévő hidrogénatomok héliumatomokká egyesülnek hatalmas hő és fény kibocsátása közben. Ebben a folyamatban a tömeg egy kis része energiává alakul át az $E=mc^2$ képlet szerint (Einstein híres egyenlete a tömeg és az energia ekvivalenciájáról). Bár a tömeg nem marad meg, a teljes energia (beleértve a tömegnek megfelelő energiát is) megmarad. A Nap által kibocsátott energia eljut a Földre, és alapvető fontosságú az élet fenntartásához.

Az Energia-megmaradás Törvényének Általánosítása

A relativitáselmélet megjelenésével Albert Einstein rámutatott a tömeg és az energia közötti szoros kapcsolatra. Az $E=mc^2$ egyenlet azt fejezi ki, hogy a tömeg is az energia egyik formája. Ezért a modern fizikában az energia-megmaradás törvényét gyakran a tömeg-energia megmaradásának törvényeként emlegetik, különösen a nukleáris fizikában és a nagy energiájú folyamatok leírásakor. Ebben az értelemben a zárt rendszer teljes tömeg-energiája marad állandó.

Következtetések: Az Energia-megmaradás Jelentősége

Az energia-megmaradás törvénye nem csupán egy fizikai elv, hanem egy alapvető keretrendszer, amely lehetővé teszi számunkra a természeti jelenségek megértését és a technológiai fejlesztéseket. Segítségével megérthetjük az erőművek működését, a járművek mozgását, a kémiai reakciók lejátszódását és a csillagok fényét. Bár az energia egyik formából a másikba átalakulhat, a teljes mennyisége mindig megmarad egy zárt rendszerben. Ez a törvény rávilágít az energia alapvető fontosságára és arra, hogy az energiaforrásaink végesek, ezért a hatékony energiafelhasználás és a fenntartható energiaforrások kutatása kiemelten fontos feladatunk.

További Vizsgálatok és Alkalmazások

Az energia-megmaradás törvénye továbbra is a modern fizika és mérnöki tudományok egyik sarokköve. Számos területen alkalmazz

Energiamegmaradas Torvenye Fogalom

Az Energiamegmaradás Törvénye: A Természet Alapvető Elve

Az energiamegmaradás törvénye a fizika egyik legfontosabb és legalapvetőbb elve, amely kimondja, hogy egy zárt rendszer teljes energiája időben állandó marad. Ez azt jelenti, hogy az energia nem keletkezhet a semmiből és nem veszhet el, csupán egyik formájából átalakulhat egy másikba. Ez a törvény áthatja a természettudományok szinte minden területét, a mechanikától a termodinamikán át az elektromágnesességig és a részecskefizikáig. Célunk, hogy ebben az átfogó cikkben részletesen feltárjuk az energiamegmaradás törvényének fogalmát, történeti hátterét, matematikai megfogalmazását, különböző megnyilvánulásait és gyakorlati alkalmazásait, ezzel biztosítva a téma lehető legmélyebb megértését.

Az Energiamegmaradás Törvényének Fogalma és Alapelvei

Az energiamegmaradás törvényének lényege, hogy a világegyetem teljes energiaállománya konstans. Bármilyen folyamat is zajlik, az energia összértéke nem változik. Amikor egy rendszer látszólag energiát veszít, az valójában egy másik formában vagy egy másik rendszerben jelenik meg. Például, amikor egy tárgy leesik, a potenciális energia mozgási energiává alakul át. Amikor egy égő gyufa fényt és hőt bocsát ki, a kémiai energia hő- és sugárzási energiává alakul. Ezek a példák jól illusztrálják az energia átalakulásának folyamatát, miközben a teljes energia mennyisége megmarad.

A Zárt Rendszer Koncepciója az Energiamegmaradásban

Az energiamegmaradás törvényének pontos megértéséhez elengedhetetlen a zárt rendszer fogalmának tisztázása. Egy zárt rendszer olyan rendszer, amely nem cserél energiát a környezetével. A valóságban tökéletesen zárt rendszerek nem léteznek, de sok fizikai modellünkben idealizált zárt rendszereket vizsgálunk a jelenségek megértéséhez. Ha egy rendszer nincs elszigetelve a környezetétől, akkor energia áramolhat be vagy ki belőle, és ebben az esetben a rendszer energiája megváltozhat. Az energiamegmaradás törvénye azonban a teljes, izolált univerzumra mindenképpen érvényesnek tekinthető.

Az Energia Különböző Formái és Átalakulásuk

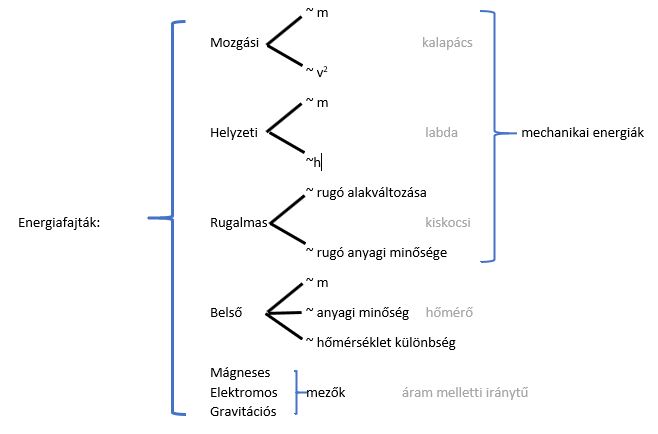
Az energia számos különböző formában létezhet, és ezek egymásba alakulhatnak. Néhány alapvető energiaforma a következő:

• Mechanikai energia: amely magában foglalja a mozgási energiát (egy test mozgásából származó energia) és a potenciális energiát (egy test helyzetéből vagy állapotából származó energia).
• Hőenergia (Termikus energia): amely az atomok és molekulák véletlenszerű mozgásával kapcsolatos energia.
• Elektromágneses energia: amely elektromos és mágneses mezőkkel kapcsolatos energia, beleértve a fényt és más elektromágneses sugárzásokat.

• Kémiai energia: amely az atomok közötti kémiai kötésekben tárolt energia.
• Nukleáris energia: amely az atommagban tárolt energia.

Az energiamegmaradás törvénye azt mondja ki, hogy egy zárt rendszerben ezen energiaformák összege állandó, bár az egyes formák egymásba alakulhatnak. Például egy vízerőműben a víz potenciális energiája mozgási energiává alakul, ami aztán elektromos energiává alakul a generátorokban.

Az Energiamegmaradás Törvényének Történeti Áttekintése

Az energiamegmaradás törvényének felismerése egy hosszú és kanyargós tudományos folyamat eredménye volt, amelyben számos tudós járult hozzá különböző meglátásaival és kísérleteivel.

A Korai Elképzelések és a Mechanikai Ekvivalens Keresése

A 17. és 18. században a tudósok, mint például Gottfried Wilhelm Leibniz, már felvetették a *vis viva* (élő erő), azaz a $mv^2$ mennyiség megmaradásának gondolatát bizonyos mechanikai kölcsönhatásokban. Bár ez nem azonos a modern értelemben vett energiával, fontos előfutára volt az energiamegmaradás elvének. A 19. század elején kezdett elterjedni az a felismerés, hogy a hő is egyfajta energia, és kapcsolatban áll a mechanikai munkával. Benjamin Thompson (gróf Rumford) híres kísérletei ágyúfúrás közben megfigyelt hőtermeléssel megkérdőjelezték a hő korábbi, anyagként való értelmezését (a kalorikus elméletet).

A Termodinamika Első Főtételének Megszületése

Az energiamegmaradás törvényének egyik legfontosabb mérföldköve a termodinamika első főtételének megfogalmazása volt a 19. század közepén. Ezt a tételt Hermann von Helmholtz, Julius Robert Mayer és James Prescott Joule egymástól függetlenül fogalmazták meg különböző formákban. Joule kísérletei különösen jelentősek voltak, amelyekkel sikerült meghatároznia a mechanikai munka és a hő közötti ekvivalenciát (a hő mechanikai egyenértékét). Mayer orvosi megfigyeléseiből kiindulva jutott el az energia megmaradásának gondolatához, míg Helmholtz átfogóbb elméleti keretet dolgozott ki. A termodinamika első főtétele formálisan kimondja, hogy egy rendszer belső energiájának megváltozása egyenlő a rendszerrel közölt hő és a rendszeren végzett munka összegével: $\Delta U = Q – W$. Ez az egyenlet az energiamegmaradás törvényének termodinamikai megfogalmazása.

Az Energiamegmaradás Általános Elvvé Válása

A termodinamika fejlődésével párhuzamosan az energiamegmaradás elve egyre általánosabb elfogadottságra tett szert a fizika más területein is. Az elektromágnesesség elméletének kidolgozása során kiderült, hogy az elektromágneses mező is energiát hordoz, és az energia megmarad az elektromágneses kölcsönhatások során is. Albert Einstein speciális relativitáselmélete tovább tágította az energiamegmaradás fogalmát azáltal, hogy megmutatta az energia és a tömeg ekvivalenciáját ($E=mc^2$), ami azt jelenti, hogy a tömeg is az energia egyik formája lehet, és átalakulhat energiává, illetve fordítva. A modern fizika minden területén, a klasszikus mechanikától a kvantummechanikán át a kozmológiáig, az energiamegmaradás törvénye alapvető axiómának számít.

Az Energiamegmaradás Törvényének Matematikai Megfogalmazása

Az energiamegmaradás törvénye matematikai formában is kifejezhető, ami lehetővé teszi a fizikai rendszerek energiaegyenségének kvantitatív leírását.

A Mechanikai Energia Megmaradása Konzervatív Erőterekben

Egy olyan rendszerben, ahol csak konzervatív erők hatnak (mint például a gravitációs erő vagy az ideális rugóerő), a mechanikai energia megmarad. A mechanikai energia a mozgási energia ($K$) és a potenciális energia ($U$) összege: $E_{mech} = K + U$. Az energiamegmaradás ebben az esetben azt jelenti, hogy a rendszer mechanikai energiája időben állandó: $\frac{dE_{mech}}{dt} = 0$, vagyis $K_1 + U_1 = K_2 + U_2$, ahol az 1-es és 2-es indexek a rendszer két különböző állapotát jelölik.

A Termodinamika Első Főtételének Matematikai Formája

Mint korábban említettük, a termodinamika első főtétele az energiamegmaradás törvényének termodinamikai megfogalmazása. Egy zárt rendszerben a belső energia ($U$) megváltozása ($\Delta U$) egyenlő a rendszerrel közölt hő ($Q$) és a rendszeren végzett munka ($W$) különbségével: $\Delta U = Q – W$. Differenciális formában ez így írható: $dU = \delta Q – \delta W$, ahol a $\delta$ jelölés azt hangsúlyozza, hogy a hő és a munka nem állapotfüggvények, hanem folyamatfüggvények.

A Noether-tétel Kapcsolata az Energiamegmaradással

A modern fizika egyik mélyreható eredménye a Noether-tétel, amely kimondja, hogy minden differenciálható szimmetriához egy megmaradó mennyiség tartozik. Az időbeli eltolási szimmetria (a fizikai törvények időben változatlanok) éppen az energia megmaradásához vezet. Ez a tétel rávilágít az energiamegmaradás törvényének alapvető jellegére a fizikai törvények szimmetriáival való mély kapcsolatán keresztül.

Különböző Energiafajták és az Energiamegmaradás

Az energiamegmaradás törvénye érvényesül az energia minden formájának átalakulása során.

Mechanikai Energia: Mozgási és Potenciális Energia

A mechanikai energia, mint említettük, a mozgási és potenciális energia összege. Egy ideális inga mozgása jó példa a mechanikai energia megmaradására (ha elhanyagoljuk a súrlódást). A legmagasabb ponton az ingának maximális potenciális energiája és nulla mozgási energiája van, míg a legalacsonyabb ponton a potenciális energia minimális (általában nullának vesszük), és a mozgási energia maximális. A köztes pontokon az energia folyamatosan átalakul a két forma között, de az összegük állandó marad.

Termikus Energia és az Energiamegmaradás

A termikus energia a rendszer belső energiájának része, amely a mikroszkopikus részecskék (atomok, molekulák) véletlenszerű mozgásával kapcsolatos. Amikor mechanikai munka hővé alakul (például súrlódás révén), vagy amikor hő hatására egy test munkát végez (például egy gáz tágulása egy hengerben), az energiamegmaradás törvénye továbbra is érvényesül. A termodinamika első főtétele éppen ezt az energiaegyenséget írja le termodinamikai rendszerekben.

Elektromágneses Energia és az Energiamegmaradás

Az elektromágneses mező energiát tárolhat és szállíthat. Például egy kondenzátor elektromos mezőben tárol energiát, míg egy induktor mágneses mezőben. Amikor egy elektromágneses hullám (például a fény) terjed, az elektromos és mágneses mezők energiát szállítanak a térben. Az energiamegmaradás itt azt jelenti, hogy az elektromágneses mező energiájának megváltozása egyenlő a rendszerrel végzett munkával és a hőcserével.

Kémiai Energia és az Energiamegmaradás

A kémiai energia a molekulákban lévő kémiai kötésekben tárolt potenciális energia. Kémiai reakciók során ezek a kötések felbomolhatnak és újak jöhetnek létre, ami energia felszabadulásával (exoterm reakciók) vagy energiafelvétellel (endoterm reakciók) járhat. Az energiamegmaradás törvénye azt biztosítja, hogy a reakcióban részt vevő anyagok energiájának és a felszabaduló vagy elnyelt energiának az összege állandó marad.

Nukleáris Energia és az Energiamegmaradás

A nukleáris energia az atommagban tárolt energia, amely a nukleonok (protonok és neutronok) közötti erős és gyenge kölcsönhatásokkal kapcsolatos. Nukleáris reakciók, mint a maghasadás (pl. atomerőművekben) vagy a magfúzió (pl. a Napban), hatalmas mennyiségű energia felszabadulásával járhatnak. Ebben az esetben az Einstein-féle $E=mc^2$ egyenlet is fontos szerepet játszik, mivel a tömeg egy része energiává alakul. Az energiamegmaradás itt a teljes energia (beleértve a tömegből származó energiát is) megmaradását jelenti.

Az Energiamegmaradás Törvényének Gyakorlati Alkalmazásai

Az energiamegmaradás törvénye nem csupán egy elméleti elv, hanem számos technológiai és mérnöki alkalmazás alapját képezi.

Energiatermelés és -átalakítás

Szinte minden energiatermelő technológia az energia egyik formájának egy másikba való átalakításán alapul, miközben az energiamegmaradás törvényét tiszteletben tartja. Például:

• Hőerőművek: Vegyi energia (pl. szénben, gázban) hőenergiává alakul, ami gőzt termel, ami turbinákat hajt meg, amelyek elektromos energiát generálnak.
• Vízerőművek: A víz potenciális energiája mozgási energiává alakul, ami turbinákat hajt meg, elektromos energiát termelve.
• Szélenergia: A szél mozgási energiája forgatja a szélturbinákat, amelyek elektromos energiát termelnek.
• Naperőművek: A nap sugárzási energiája közvetlenül (fotovoltaikus panelekben) vagy közvetetten (hőerőművekben) elektromos energiává alakul.

Mindegyik esetben az energia egyik formája alakul át egy másikba, a teljes energia mennyisége pedig megmarad (bár egy része hasznos munkavégzés helyett gyakran hő formájában “veszteségként” jelentkezik).

Közlekedés

A közlekedési eszközök működése is az energiamegmaradás törvényén alapul. Egy autóban a benzin kémiai energiája hővé és mozgási energiává alakul. Egy elektromos autóban az akkumulátorban tárolt kémiai energia elektromos energiává alakul, ami a motort hajtja meg, mozg

Munka Energia Teljesitmeny Feladatok Megoldassal

A Munka, Energia és Teljesítmény Világa: Átfogó Útmutató Feladatokkal és Részletes Megoldásokkal

Ebben a kimerítő cikkben mélyrehatóan feltárjuk a munka, az energia és a teljesítmény alapvető fogalmait a fizikában. Nem csupán definíciókkal szolgálunk, hanem részletes magyarázatokon keresztül vezetjük végig Olvasóinkat, illusztratív példákkal és gondosan kidolgozott feladatokkal segítve a megértést. Célunk, hogy Ön ne csak elsajátítsa ezeket a kulcsfontosságú fizikai elveket, hanem képes legyen azokat magabiztosan alkalmazni a legkülönfélébb problémák megoldása során.

A Munka Fogalma a Fizikában: Több, Mint Pusztán Fáradozás

A hétköznapi nyelvhasználattól eltérően a fizikában a munka egy precízen definiált fogalom. Akkor végzünk munkát egy testtel, ha egy erő hatására a test elmozdul az erő irányában (vagy az erő elmozdulás irányú komponense mentén). Matematikailag a munka (W) a testre ható erő (\\mathbf\{F\}) és az elmozdulás (\\mathbf\{d\}) skaláris szorzataként definiálható:

\\mathbf\{W\} \= \\mathbf\{F\} \\cdot \\mathbf\{d\} \= \|\\mathbf\{F\}\| \|\\mathbf\{d\}\| \\cos \\theta

ahol \|\\mathbf\{F\}\| az erő nagysága, \|\\mathbf\{d\}\| az elmozdulás nagysága, és \\theta az erő és az elmozdulás közötti szög. A munka mértékegysége a Joule (J), amely megegyezik az 1 Newton szorozva 1 méterrel (1 N⋅m).

Példa a Munka Számítására

Képzeljünk el egy esetet, ahol egy 10 N nagyságú vízszintes erővel eltolunk egy dobozt 5 méteren keresztül egy vízszintes felületen. Mivel az erő és az elmozdulás azonos irányú, a \\cos \\theta \= \\cos 0^\\circ \= 1. Így a végzett munka:

W \= \(10 \\, \\text\{N\}\) \\times \(5 \\, \\text\{m\}\) \\times 1 \= 50 \\, \\text\{J\}

Feladat 1: Munkavégzés Ferde Erővel

Egy 2 kg tömegű testet egy vízszintes felületen húzunk egy 20 N nagyságú erővel, amely a vízszintessel 30 fokos szöget zár be. Mekkora munkát végzünk, ha a test 3 métert mozdul el?

Megoldás:

Az erő vízszintes komponense F\_x \= \|\\mathbf\{F\}\| \\cos \\theta \= 20 \\, \\text\{N\} \\times \\cos 30^\\circ \= 20 \\, \\text\{N\} \\times \\frac\{\\sqrt\{3\}\}\{2\} \\approx 17\.32 \\, \\text\{N\}.

A végzett munka W \= F\_x \\times d \= 17\.32 \\, \\text\{N\} \\times 3 \\, \\text\{m\} \\approx 51\.96 \\, \\text\{J\}.

Az Energia Sokszínű Formái: A Munkavégzés Lehetősége

Az energia egy test vagy rendszer azon képessége, hogy munkát végezzen. Számos formában létezik, beleértve a kinetikus energiát (mozgás energiája), a potenciális energiát (helyzetből vagy állapotból származó energia), a termikus energiát (hő), a kémiai energiát, a nukleáris energiát és a sugárzási energiát. Az energia mértékegysége szintén a Joule (J).

Kinetikus Energia: A Mozgásban Rejlő Erő

Egy m tömegű, v sebességgel mozgó test kinetikus energiája (K) a következőképpen számítható:

K \= \\frac\{1\}\{2\} m v^2

Minél nagyobb a test tömege vagy sebessége, annál nagyobb a kinetikus energiája, és annál több munkát képes végezni a megállásáig.

Potenciális Energia: A Helyzetből Adódó Lehetőség

A potenciális energia egy test helyzetéből vagy konfigurációjából adódik. A leggyakrabban tárgyalt formái a gravitációs potenciális energia és a rugalmas potenciális energia.

Gravitációs Potenciális Energia

Egy m tömegű testnek a Föld felszínétől h magasságban lévő gravitációs potenciális energiája (U\_g) a következőképpen adható meg:

U\_g \= mgh

ahol g a gravitációs gyorsulás (kb. 9\.81 \\, \\text\{m/s\}^2 a Föld felszínén).

Rugalmas Potenciális Energia

Egy k rugóállandójú rugóban, amely x méterrel van megnyújtva vagy összenyomva, tárolt rugalmas potenciális energia (U\_e) a következőképpen számítható:

U\_e \= \\frac\{1\}\{2\} k x^2

Feladat 2: Kinetikus és Potenciális Energia

Egy 0.5 kg tömegű labdát 10 m/s sebességgel függőlegesen feldobunk a földről. Mekkora a labda kinetikus energiája a feldobás pillanatában? Mekkora a gravitációs potenciális energiája a legmagasabb ponton, ha a légellenállást elhanyagoljuk?

Megoldás:

A feldobás pillanatában a kinetikus energia: K \= \\frac\{1\}\{2\} \(0\.5 \\, \\text\{kg\}\) \(10 \\, \\text\{m/s\}\)^2 \= 25 \\, \\text\{J\}.

A legmagasabb ponton a kinetikus energia nulla (a labda pillanatnyi sebessége nulla). Az összes kezdeti kinetikus energia gravitációs potenciális energiává alakul. Így a legmagasabb ponton a potenciális energia is 25 J.

A Munkatétel: Kapocs a Munka és az Energia Között

A munkatétel egy alapvető elv a mechanikában, amely kimondja, hogy egy testre ható összes erő által végzett nettó munka egyenlő a test kinetikus energiájának megváltozásával:

W\_\{netto\} \= \\Delta K \= K\_f \- K\_i \= \\frac\{1\}\{2\} m v\_f^2 \- \\frac\{1\}\{2\} m v\_i^2

Ez a tétel rendkívül hasznos a mozgás elemzésében, különösen akkor, ha az erők nem állandóak.

Feladat 3: A Munkatétel Alkalmazása

Egy 1000 kg tömegű autó álló helyzetből indul, és egy állandó eredő erő hatására 20 m/s sebességet ér el 100 méter megtétele után. Mekkora volt az eredő erő?

Megoldás:

A kinetikus energia megváltozása: \\Delta K \= \\frac\{1\}\{2\} \(1000 \\, \\text\{kg\}\) \(20 \\, \\text\{m/s\}\)^2 \- \\frac\{1\}\{2\} \(1000 \\, \\text\{kg\}\) \(0 \\, \\text\{m/s\}\)^2 \= 200000 \\, \\text\{J\}.

A munkatétel szerint W\_\{netto\} \= \\Delta K, így F\_\{netto\} \\times d \= 200000 \\, \\text\{J\}.

Az eredő erő F\_\{netto\} \= \\frac\{200000 \\, \\text\{J\}\}\{100 \\, \\text\{m\}\} \= 2000 \\, \\text\{N\}.

Az Energia Megmaradásának Törvénye: Egyetemes Elv

Az energia megmaradásának törvénye az egyik legalapvetőbb és legszélesebb körben érvényesülő természeti törvény. Kimondja, hogy egy zárt rendszer teljes energiája állandó marad az időben. Az energia átalakulhat egyik formából a másikba, de nem keletkezhet és nem veszhet el.

Példa az Energia Megmaradására

Egy inga lengése során a gravitációs potenciális energia folyamatosan kinetikus energiává alakul, amikor az inga lefelé mozog, és fordítva, a kinetikus energia potenciális energiává alakul, amikor az inga felfelé lendül. Ha elhanyagoljuk a súrlódást és a légellenállást, a rendszer mechanikai energiája (a kinetikus és potenciális energia összege) állandó marad.

Feladat 4: Energia Megmaradás Inga Esetén

Egy 1 kg tömegű inga 1 méter hosszú fonálon lóg. Az ingát vízszintes helyzetből elengedjük. Mekkora lesz az inga sebessége a legalsó ponton?

Megoldás:

A kezdeti helyzetben az ingának csak gravitációs potenciális energiája van a legalsó ponthoz képest: U\_i \= mgh \= \(1 \\, \\text\{kg\}\) \(9\.81 \\, \\text\{m/s\}^2\) \(1 \\, \\text\{m\}\) \= 9\.81 \\, \\text\{J\}. A kezdeti kinetikus energia nulla.

A legalsó ponton a gravitációs potenciális energia nulla, és az összes kezdeti potenciális energia kinetikus energiává alakul: K\_f \= \\frac\{1\}\{2\} m v\_f^2.

Az energia megmaradásának törvénye szerint U\_i \= K\_f, így 9\.81 \\, \\text\{J\} \= \\frac\{1\}\{2\} \(1 \\, \\text\{kg\}\) v\_f^2.

Ebből a sebesség v\_f \= \\sqrt\{\\frac\{2 \\times 9\.81 \\, \\text\{J\}\}\{1 \\, \\text\{kg\}\}\} \\approx 4\.43 \\, \\text\{m/s\}.

A Teljesítmény Fogalma: A Munkavégzés Sebessége

A teljesítmény (P) azt adja meg, hogy milyen gyorsan végeznek munkát, vagy milyen gyorsan alakul át az energia. Matematikailag a teljesítmény a végzett munka és az eltelt idő hányadosa:

P \= \\frac\{W\}\{t\}

A teljesítményt az energia idő szerinti deriváltjaként is definiálhatjuk:

P \= \\frac\{dE\}\{dt\}

A teljesítmény mértékegysége a Watt (W), amely megegyezik az 1 Joule per másodperccel (1 J/s).

Teljesítmény Állandó Erő Esetén

Ha egy állandó \\mathbf\{F\} erő egy testet \\mathbf\{v\} sebességgel mozgat, akkor a teljesítmény:

P \= \\mathbf\{F\} \\cdot \\mathbf\{v\} \= \|\\mathbf\{F\}\| \|\\mathbf\{v\}\| \\cos \\phi

ahol \\phi az erő és a sebesség közötti szög.

Feladat 5: Teljesítmény Számítása

Egy daru egy 500 kg tömegű terhet 10 méter magasra emel fel 20 másodperc alatt állandó sebességgel. Mekkora a daru által kifejtett átlagos teljesítmény?

Megoldás:

A daru által végzett munka a gravitáció ellenében: W \= mgh \= \(500 \\, \\text\{kg\}\) \(9\.81 \\, \\text\{m/s\}^2\) \(10 \\, \\text\{m\}\) \= 49050 \\, \\text\{J\}.

Az átlagos teljesítmény: P \= \\frac\{W\}\{t\} \= \\frac\{49050 \\, \\text\{J\}\}\{20 \\, \\text\{s\}\} \= 2452\.5 \\, \\text\{W\}.

A Hatásfok: A Hasznos Munkavégzés Mértéke

A valóságban az energiaátalakítások sosem tökéletesek; mindig van valamennyi energiaveszteség, leggyakrabban hő formájában. A hatásfok (\\eta) azt adja meg, hogy egy rendszer a befektetett energiának vagy munkának mekkora hányadát képes hasznos munkává vagy energiává alakítani:

\\eta \= \\frac\{W\_\{hasznos\}\}\{W\_\{befektetett\}\} \= \\frac\{E\_\{hasznos\}\}\{E\_\{befektetett\}\}

A hatásfok mindig 0 és 1 (vagy 0% és 100%) közötti érték.

Példa a Hatásfokra

Egy elektromos motor 1000 J elektromos energiát vesz fel, és ennek hatására 800 J mechanikai munkát végez. A motor hatásfoka \\eta \= \\frac\{800 \\, \\text\{J\}\}\{1000 \\, \\text\{J\}\} \= 0\.8, vagyis 80%.

Feladat 6: Hatásfok Számítása

Egy benzinmotor 50000 J kémiai energiát alakít át, miközben 12500 J mechanikai munkát végez. Mekkora a motor hatásfoka?

Megoldás:

A motor hatásfoka: \\eta \= \\frac\{12500 \\, \\text\{J\}\}\{50000 \\, \\text\{J\}\} \= 0\.25, vagyis 25%.

További Összetett Feladatok a Munka, Energia és Teljesítmény Témakörében

Összetett Feladat 1: Lejtőn Csúszó Test

Egy 5 kg tömegű test egy 30

Mechanikai Energiafajtak

A Mechanikai Energia Fajtái: Átfogó Kézikönyv

A mechanikai energia a fizika egyik alapvető fogalma, amely egy test vagy rendszer mozgásával és helyzetével kapcsolatos energiát írja le. Ez az energiaforma kulcsfontosságú a makroszkopikus világ jelenségeinek megértéséhez, a mindennapi tapasztalatainktól kezdve a komplex mérnöki alkalmazásokig. Ebben a részletes útmutatóban feltárjuk a mechanikai energia különböző fajtáit, azok jellemzőit, megjelenési formáit és a velük kapcsolatos alapvető fizikai törvényeket.

A Mechanikai Energia Alapjai

A mechanikai energia fogalma szorosan kapcsolódik a munkavégzés képességéhez. Ha egy erő egy testet elmozdít, munkát végez rajta, és ez a munka megváltoztathatja a test mechanikai energiáját. A mechanikai energia két fő összetevőre bontható: a kinetikus energiára és a potenciális energiára. Ezek az energiafajták együttesen határozzák meg egy rendszer teljes mechanikai energiáját.

Kinetikus Energia: A Mozgás Energiája

A kinetikus energia egy test mozgásából származó energia. Minden olyan objektum, amely mozog, rendelkezik kinetikus energiával. Ennek az energiának a nagysága függ a test tömegétől és sebességétől. Minél nagyobb a test tömege vagy sebessége, annál nagyobb a kinetikus energiája. A kinetikus energia képlete a következő:

\\mathbf\{E\_k \= \\frac\{1\}\{2\}mv^2\}

ahol \(E_k\) a kinetikus energia, \(m\) a test tömege, és \(v\) a test sebessége.

Példák a Kinetikus Energiára

• Egy száguldó autó: Minél gyorsabban halad az autó, annál nagyobb a kinetikus energiája. Egy nehezebb autó azonos sebességnél szintén nagyobb kinetikus energiával rendelkezik.
• Egy repülő labda: A labda mozgása során kinetikus energiával rendelkezik. A dobás erőssége és a labda tömege befolyásolja ezt az energiát.
• Egy forgó kerék: A forgó kerék részei folyamatos mozgásban vannak, így a kerék rendelkezik kinetikus energiával.

A kinetikus energia nem csak a lineáris mozgáshoz kapcsolódik, hanem a forgó mozgáshoz is. A forgó testek forgási kinetikus energiával rendelkeznek, amely a test tehetetlenségi nyomatékától és szögsebességétől függ.

\\mathbf\{E\_\{rot\} \= \\frac\{1\}\{2\}I\\omega^2\}

ahol \(E_{rot}\) a forgási kinetikus energia, \(I\) a tehetetlenségi nyomaték, és \(\omega\) a szögsebesség.

Potenciális Energia: A Helyzetből Adódó Energia

A potenciális energia egy test helyzetéből vagy konfigurációjából származó tárolt energia. Ez az energia akkor szabadulhat fel, ha a test megváltoztatja a helyzetét vagy konfigurációját. A mechanikában két fő típusa van a potenciális energiának: a gravitációs potenciális energia és a rugalmas potenciális energia.

Gravitációs Potenciális Energia

A gravitációs potenciális energia egy testnek a gravitációs mezőben elfoglalt helyzetéből adódik. A Föld felszínén egy \(h\) magasságban lévő \(m\) tömegű test gravitációs potenciális energiája a következőképpen számítható ki:

\\mathbf\{E\_p \= mgh\}

ahol \(E_p\) a gravitációs potenciális energia, \(m\) a test tömege, \(g\) a gravitációs gyorsulás (a Földön körülbelül \(9.81 \, m/s^2\)), és \(h\) a test magassága egy referencia szinthez képest.

Példák a Gravitációs Potenciális Energiára

• Egy hegy tetején lévő kő: A kőnek magasságából adódóan gravitációs potenciális energiája van. Ha a kő leesik, ez az energia kinetikus energiává alakul át.
• Egy víztározóban lévő víz: A magasabban lévő víz gravitációs potenciális energiával rendelkezik, amelyet a vízerőművek elektromos áram előállítására használnak fel.
• Egy fán lévő alma: Az almának a földfelszínhez viszonyított magassága miatt gravitációs potenciális energiája van. Amikor leesik, ez az energia mozgási energiává alakul.

Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmasan deformálható test (például egy rugó vagy egy gumiszalag) megfeszítéséből vagy összenyomásából származik. A rugalmas erővel szemben végzett munka tárolódik ebben az energiaformában. Egy ideális rugó rugalmas potenciális energiája a következőképpen adható meg:

\\mathbf\{E\_\{elas\} \= \\frac\{1\}\{2\}kx^2\}

ahol \(E_{elas}\) a rugalmas potenciális energia, \(k\) a rugóállandó (amely a rugó merevségét jellemzi), és \(x\) a rugó egyensúlyi helyzetétől való elmozdulása.

Példák a Rugalmas Potenciális Energiára

• Egy megfeszített rugó: Amikor egy rugót megfeszítünk vagy összenyomunk, rugalmas potenciális energiát tárol. Ez az energia szabadul fel, amikor a rugó visszatér eredeti alakjába.
• Egy kilőtt nyíl: A megfeszített íj húrjában tárolt rugalmas potenciális energia alakul át a nyíl kinetikus energiájává.
• Egy trambulin: Amikor valaki ráugrik a trambulinra, a rugók megfeszülnek, rugalmas potenciális energiát tárolva, amely aztán visszalökő erőt fejt ki.

A Mechanikai Energia Megmaradása

Az egyik legfontosabb elv a fizikában az energia megmaradásának törvénye, amely kimondja, hogy egy zárt rendszer teljes energiája állandó marad, feltéve, hogy nincsenek nem-konzervatív erők (például súrlódás vagy légellenállás) munkája. A mechanikai energia esetében ez azt jelenti, hogy egy olyan rendszerben, ahol csak konzervatív erők hatnak, a kinetikus energia és a potenciális energia összege állandó marad:

\\mathbf\{E\_\{mech\} \= E\_k \+ E\_p \= állandó\}

Példák az Energia Megmaradására

• Egy ingamozgás: Amikor az inga a legmagasabb pontján van, a potenciális energiája maximális, a kinetikus energiája pedig nulla. Ahogy az inga lefelé mozog, a potenciális energia kinetikus energiává alakul át. A legalacsonyabb ponton a kinetikus energia maximális, a potenciális energia pedig minimális. Ideális esetben a teljes mechanikai energia (a kinetikus és a potenciális energia összege) állandó marad.

• Egy leeső tárgy: Amikor egy tárgyat elejtünk, a kezdeti magasságban gravitációs potenciális energiával rendelkezik. Ahogy esik, ez az energia fokozatosan kinetikus energiává alakul át. Közvetlenül a földbe csapódás előtt a kinetikus energia maximális, a potenciális energia pedig minimális (a referencia szinttől függően).

Nem-Konzervatív Erők és a Mechanikai Energia Disszipációja

A valóságban gyakran vannak jelen nem-konzervatív erők, mint például a súrlódás és a légellenállás. Ezek az erők munkát végeznek a rendszeren, és ez a munka nem tárolódik potenciális energiaként, hanem általában hővé alakul. Ebben az esetben a teljes mechanikai energia nem marad meg, hanem csökken. Ezt az energiacsökkenést disszipációnak nevezzük.

Példák a Mechanikai Energia Disszipációjára

• Egy csúszó tárgy: Amikor egy tárgy egy felületen csúszik, a súrlódási erő munkát végez, és a mechanikai energia egy része hővé alakul, felmelegítve a tárgyat és a felületet. Ennek eredményeként a tárgy mozgása lelassul és végül megáll.
• Egy fékező autó: Az autó fékezése során a kinetikus energia a fékekben súrlódási hővé alakul, ami lelassítja az autót.

A Mechanikai Energia Átalakulásai

A mechanikai energia különböző formái egymásba alakulhatnak. Láttuk már a potenciális energia kinetikus energiává való átalakulását egy leeső tárgy vagy egy inga esetében, és fordítva, a kinetikus energia potenciális energiává alakulását egy felfelé dobott labda esetében, amely eléri a legmagasabb pontját.

További Példák az Energia Átalakulásaira

• Egy vízerőmű: A víztározóban lévő víz gravitációs potenciális energiája a turbinákon átfolyva kinetikus energiává alakul, amely aztán elektromos generátort hajt meg.
• Egy autó motorja: A benzin kémiai energiája először hővé, majd a mozgó alkatrészek révén mechanikai energiává alakul.
• Egy szélmalom: A szél kinetikus energiája a lapátokat forgatva mechanikai energiává alakul, amelyet aztán különböző célokra lehet felhasználni.

A Mechanikai Energia Jelentősége és Alkalmazásai

A mechanikai energia megértése és hasznosítása alapvető fontosságú számos tudományterületen és technológiai alkalmazásban.

Mérnöki Alkalmazások

• Gépészet: A gépek tervezése és működtetése a mechanikai energia átalakításán és továbbításán alapul.
• Építőmérnökség: Az épületek és hidak stabilitásának és a terhelések elviselésének megértéséhez elengedhetetlen a mechanikai erők és energiák ismerete.

• Repüléstechnika: A repülőgépek mozgása és a felhajtóerő létrehozása a mechanikai elveken alapul.

Mindennapi Élet

• A közlekedési eszközök (autók, vonatok, kerékpárok) mechanikai energiát használnak a mozgáshoz.
• A háztartási gépek (mosógép, turmixgép) működéséhez mechanikai energiára van szükség.
• A sporteszközök (labdák, ütők) használata során a mechanikai energia átalakulásai figyelhetők meg.

Összefoglalás

A mechanikai energia a mozgással és a helyzettel kapcsolatos energia. Két fő fajtája van: a kinetikus energia (a mozgás energiája) és a potenciális energia (a helyzetből adódó tárolt energia, amely lehet gravitációs vagy rugalmas). Egy zárt rendszerben, ahol csak konzervatív erők hatnak, a mechanikai energia megmarad. A valóságban azonban nem-konzervatív erők is jelen lehetnek, amelyek a mechanikai energia disszipációjához vezetnek. A mechanikai energia megértése kulcsfontosságú a természeti jelenségek és a technológiai alkalmazások széles körének megértéséhez.

További Tudnivalók a Mechanikai Energiáról

A mechanikai energia fogalmának mélyebb megértéséhez érdemes megvizsgálni a munka-energia tételt is, amely összekapcsolja a munkát és az energiaváltozást. A tétel kimondja, hogy egy testre ható összes erő által végzett munka egyenlő a test kinetikus energiájának megváltozásával:

\\mathbf\{W\_\{net\} \= \\Delta E\_k \= E\_\{k,f\} \- E\_\{k,i\}\}

ahol \(W_{net}\) a nettó munka, \(\Delta E_k\) a kinetikus energia változása, \(E_{k,f}\) a végső kinetikus energia, és \(E_{k,i}\) a kezdeti kinetikus energia.

A Konzervatív Erők és a Potenciális Energia Kapcsolata

A potenciális energia fogalma szorosan kapcsolódik a konzervatív erőkkel. Egy erő akkor konzervatív, ha az általa végzett munka egy zárt úton nulla, vagy ha a két pont között végzett munka független az útvonaltól. A gravitációs erő és a rugalmas erő tipikus példái a konzervatív erőknek. A potenciális energia definíció szerint a konzervatív erő által végzett munka negatívja:

\\mathbf\{\\Delta U \= \-W\_c\}

ahol \(\Delta U\) a potenciális energia változása, és \(W_c\) a konzervatív erő által végzett munka.

A Mechanikai Energia Mérésének Egységei

A mechanikai energiát (mind a kinetikus, mind a potenciális formában) a Nemzetközi Mértékegységrendszerben (SI) joule-ban (J) mérik. Egy joule egyenlő egy newton méterrel (N·m), vagy alapegységekben \(kg \cdot m^2/s^2\).

Komplexebb Rendszerek Mechanikai Energiája

Több testből álló rendszerek esetében a teljes mechanikai energia az egyes testek kinetikus és potenciális energiáinak összege. Például egy bolygórendszerben a bolygók kinetikus energiájának és a bolygók közötti gravitációs potenciális energiának az összege adja a rendszer teljes mechanikai energiáját.

Molekuláris szintű Mechanikai Energia

Bár a mechanikai energia fogalmát leggyakrabban makroszkopikus objektum