Penzugyi Elemzes Minta

Átfogó Pénzügyi Elemzés Minta: Részletes Útmutató a Sikeres Értékeléshez

Üdvözöljük átfogó útmutatónkban a pénzügyi elemzés világában! Célunk, hogy egy részletes mintán keresztül bemutassuk Önnek a pénzügyi adatok értelmezésének és a megalapozott döntések meghozatalának kulcsfontosságú lépéseit. Legyen szó befektetőről, vállalkozóról vagy pénzügyi szakemberről, ez a cikk elengedhetetlen tudást nyújt a sikeres pénzügyi elemzéshez.

A Pénzügyi Elemzés Alapjai és Fontossága

A pénzügyi elemzés egy olyan folyamat, amelynek során egy szervezet vagy egy befektetés múltbeli, jelenlegi és jövőbeli pénzügyi teljesítményét értékeljük. Ez magában foglalja a pénzügyi kimutatások, mint a mérleg, az eredménykimutatás és a cash flow kimutatás részletes vizsgálatát, valamint különböző pénzügyi mutatók kiszámítását és értelmezését. A pénzügyi elemzés elengedhetetlen a tájékozott üzleti és befektetési döntések meghozatalához, segít azonosítani a trendeket, feltárni a gyengeségeket és megerősíteni az erősségeket.

Miért Nélkülözhetetlen a Pénzügyi Elemzés?

A pénzügyi elemzés számos előnnyel jár. Segít:

• A vállalat pénzügyi helyzetének és teljesítményének megértésében.
• A jövőbeli pénzügyi teljesítmény előrejelzésében.

• A befektetési lehetőségek értékelésében.
• A kockázatok azonosításában és kezelésében.
• A vezetőségi döntések megalapozásában.
• A versenytársak pénzügyi teljesítményének összehasonlításában.

A Pénzügyi Kimutatások Részletes Áttekintése

A pénzügyi elemzés alapját a pénzügyi kimutatások képezik. Nézzük meg a legfontosabbakat részletesen:

A Mérleg (Balance Sheet)

A mérleg egy adott időpontra vonatkozóan mutatja be egy vállalat eszközeit, forrásait (saját tőke és kötelezettségek) és azok egyenségét. Alapvető képlete:

\\text\{Eszközök\} \= \\text\{Saját tőke\} \+ \\text\{Kötelezettségek\}

A mérleg áttekintést nyújt a vállalat likviditásáról, eladósodottságáról és tőkeszerkezetéről.

A Mérleg Főbb Elemei:

• Eszközök: Mindaz, amivel a vállalat rendelkezik és ami gazdasági előnyökkel járhat a jövőben. Ide tartoznak a forgóeszközök (pl. készpénz, követelések, készletek) és a befektetett eszközök (pl. ingatlanok, gépek, berendezések, immateriális javak).
• Kötelezettségek: A vállalat külső felekkel szembeni tartozásai. Megkülönböztetünk rövid lejáratú (pl. szállítói tartozások, rövid lejáratú hitelek) és hosszú lejáratú kötelezettségeket (pl. hosszú lejáratú hitelek, kötvények).
• Saját tőke: A tulajdonosok befektetése a vállalatba, valamint a megtermelt és visszaforgatott eredmény. Ide tartozik a jegyzett tőke, a tőketartalék, az eredménytartalék és az adózott eredmény.

Az Eredménykimutatás (Income Statement)

Az eredménykimutatás egy adott időszak (általában egy év vagy egy negyedév) alatt elért bevételeket, ráfordításokat és az ezek különbségeként adódó eredményt (profitot vagy veszteséget) mutatja be. Alapvető felépítése:

\\text\{Bevételek\} \- \\text\{Ráfordítások\} \= \\text\{Eredmény\}

Az eredménykimutatás segít megérteni a vállalat jövedelmezőségét és hatékonyságát.

Az Eredménykimutatás Főbb Elemei:

• Nettó árbevétel: Az értékesítésből származó bevétel, csökkentve a visszáruval és az engedményekkel.
• Értékesítés közvetlen költsége (ELÁBÉ): Az eladott termékek vagy szolgáltatások előállításának közvetlen költségei.
• Bruttó eredmény: A nettó árbevétel és az ELÁBÉ különbsége.

• Működési költségek: A vállalat napi működésével kapcsolatos költségek (pl. bérköltség, marketing költség, adminisztratív költségek).
• Működési eredmény: A bruttó eredmény és a működési költségek különbsége.
• Pénzügyi eredmény: A pénzügyi bevételek (pl. kamatbevételek) és ráfordítások (pl. kamatkiadások) egyenlege.
• Adózás előtti eredmény: A működési eredmény és a pénzügyi eredmény összege.
• Adófizetési kötelezettség: A társasági adó összege.
• Nettó eredmény: Az adózás előtti eredmény és az adófizetési kötelezettség különbsége (a vállalat végső profitja vagy vesztesége).

A Cash Flow Kimutatás (Statement of Cash Flows)

A cash flow kimutatás egy adott időszak alatt a vállalat pénzmozgásait mutatja be. Három fő részre oszlik:

• Működési cash flow: A vállalat fő üzleti tevékenységéből származó pénzbevételek és -kiadások.
• Befektetési cash flow: A befektetési eszközök (pl. ingatlanok, gépek, berendezések) vásárlásából és eladásából származó pénzmozgások.
• Finanszírozási cash flow: A vállalat finanszírozásával kapcsolatos pénzmozgások (pl. hitelfelvétel, tőkeemelés, osztalékfizetés).

A cash flow kimutatás kulcsfontosságú a vállalat likviditásának megértéséhez és a pénzügyi stabilitásának megítéléséhez.

Pénzügyi Mutatók: A Teljesítmény Értékelésének Eszközei

A pénzügyi mutatók a pénzügyi kimutatások adataiból képzett arányszámok, amelyek segítenek a vállalat pénzügyi helyzetének és teljesítményének számszerű értékelésében. Számos különböző mutató létezik, amelyeket különböző célokra használnak.

Likviditási Mutatók

A likviditási mutatók azt mérik, hogy a vállalat mennyire képes rövid távú kötelezettségeit időben teljesíteni.

• Folyó hányad (Current Ratio):

  \\text\{Folyó hányad\} \= \\frac\{\\text\{Forgóeszközök\}\}\{\\text\{Rövid lejáratú kötelezettségek\}\}

  Egy általánosan elfogadott érték az 1,5-2 közötti tartomány, de ez iparágfüggő lehet.

• Gyorsráta (Quick Ratio vagy Acid-Test Ratio):

  \\text\{Gyorsráta\} \= \\frac\{\\text\{Forgóeszközök\} \- \\text\{Készletek\}\}\{\\text\{Rövid lejáratú kötelezettségek\}\}

  A készleteket nem veszi figyelembe, így pontosabb képet adhat a vállalat azonnali fizetőképességéről. Egy elfogadható érték általában 1 körül van.

Jövedelmezőségi Mutatók

A jövedelmezőségi mutatók azt mérik, hogy a vállalat mennyire hatékonyan képes profitot termelni.

• Bruttó árrés (Gross Profit Margin):

  \\text\{Bruttó árrés\} \= \\frac\{\\text\{Bruttó eredmény\}\}\{\\text\{Nettó árbevétel\}\} \\times 100\\%

  Megmutatja, hogy az árbevétel hány százaléka marad meg a közvetlen költségek levonása után.

  
• Működési árrés (Operating Profit Margin):

  \\text\{Működési árrés\} \= \\frac\{\\text\{Működési eredmény\}\}\{\\text\{Nettó árbevétel\}\} \\times 100\\%

  Megmutatja a vállalat operatív tevékenységének jövedelmezőségét.

• Nettó árrés (Net Profit Margin):

  \\text\{Nettó árrés\} \= \\frac\{\\text\{Nettó eredmény\}\}\{\\text\{Nettó árbevétel\}\} \\times 100\\%

  Megmutatja, hogy az árbevétel hány százaléka marad meg az összes költség (beleértve az adót és a kamatokat) levonása után.

• Sajáttőke-arányos megtérülés (ROE – Return on Equity):

  \\text\{ROE\} \= \\frac\{\\text\{Nettó eredmény\}\}\{\\text\{Saját tőke\}\} \\times 100\\%

  Megmutatja, hogy a tulajdonosok befektetése mennyire hatékonyan termel profitot.

• Eszközarányos megtérülés (ROA – Return on Assets):

  \\text\{ROA\} \= \\frac\{\\text\{Nettó eredmény\}\}\{\\text\{Összes eszköz\}\} \\times 100\\%

  Megmutatja, hogy a vállalat eszközei mennyire hatékonyan termelnek profitot.

Eladósodottsági Mutatók

Az eladósodottsági mutatók azt mérik, hogy a vállalat milyen mértékben támaszkodik külső finanszírozásra.

• Idegen tőke aránya (Debt-to-Equity Ratio):

  \\text\{Idegen tőke aránya\} \= \\frac\{\\text\{Összes kötelezettség\}\}\{\\text\{Saját tőke\}\}

  Megmutatja a saját tőke és az idegen tőke arányát a vállalat finanszírozásában. Egy magas érték magasabb pénzügyi kockázatot jelezhet.

• Adósságszolgálat fedezeti mutató (Debt Service Coverage Ratio – DSCR):

  \\text\{DSCR\} \= \\frac\{\\text\{Működési eredmény\} \+ \\text\{Értékcsökkenés\}\}\{\\text\{Törlesztések\} \+ \\text\{Kamatfizetések\}\}

  Megmutatja, hogy a vállalat mennyire képes fedezni adósságszolgálatát a működési cash flow-ból.

Hatékonysági Mutatók

A hatékonysági mutatók azt mérik, hogy a vállalat mennyire hatékonyan használja fel eszközeit és forrásait.

• Készletforgási sebesség (Inventory Turnover):

  \\text\{Készletforgási sebesség\} \= \\frac\{\\text\{Értékesítés közvetlen költsége\}\}\{\\text\{Átlagos készlet\}\}

  Megmutatja, hányszor adja el és tölti fel készleteit a vállalat egy adott időszak alatt. Egy magas érték hatékony készletgazdálkodást jelezhet.

• Követelések forgási sebessége (Receivables Turnover):

  \\text\{Követelések forgási sebessége\} \= \\frac\{\\text\{Nettó árbevétel\}\}\{\\text\{Átlagos követelések\}\}

  Megmutatja, hányszor térülnek meg a követelések egy adott időszak alatt. Egy magas érték hatékony követeléskezelést jelezhet.

• Eszközök forgási sebessége (Asset Turnover):

  \\text\{Eszközök forgási sebessége\} \= \\frac\{\\text\{Nettó árbevétel\}\}\{\\text\{Átlagos összes eszköz\}\}

  Megmutatja, hogy a vállalat eszközei mennyire hatékonyan generálnak árbevételt.

Pénzügyi Elemzési Módszerek

A pénzügyi elemzés során többféle módszert alkalmazhatunk a pénzügyi kimutatások és a mutatók értelmezésére.

Trendelemzés (Trend Analysis)

A trendelemzés során a pénzügyi adatok időbeli változásait vizsgáljuk. Ez segíthet azonosítani a pozitív vagy negatív tendenciákat a vállalat pénzügyi teljesítményében.

Vertikális Elemzés (Vertical Analysis)

A vertikális elemzés során a pénzügyi kimutatások egyes tételeinek arányát vizsgáljuk egy bázisösszeghez képest. Például az eredménykimutatásban minden tételt a nettó árbevétel százalékában fejezünk ki, a mérlegben pedig az összes eszköz vagy az összes forrás százalékában.

Horizontális Elemzés (Horizontal Analysis)

A horizontális elemzés során a pénzügyi kimutatások egyes tételeinek változását vizsgáljuk két vagy több időszak között. Gyakran százalékos változásokat számítunk.

Összehasonlító Elemzés (Ratio Analysis)

Az összehasonlító elemzés során a vállalat pénzügyi mutatóit összehasonlítjuk korábbi időszakok mutatóival, a versenytársak mutatóival vagy iparági átlagokkal.

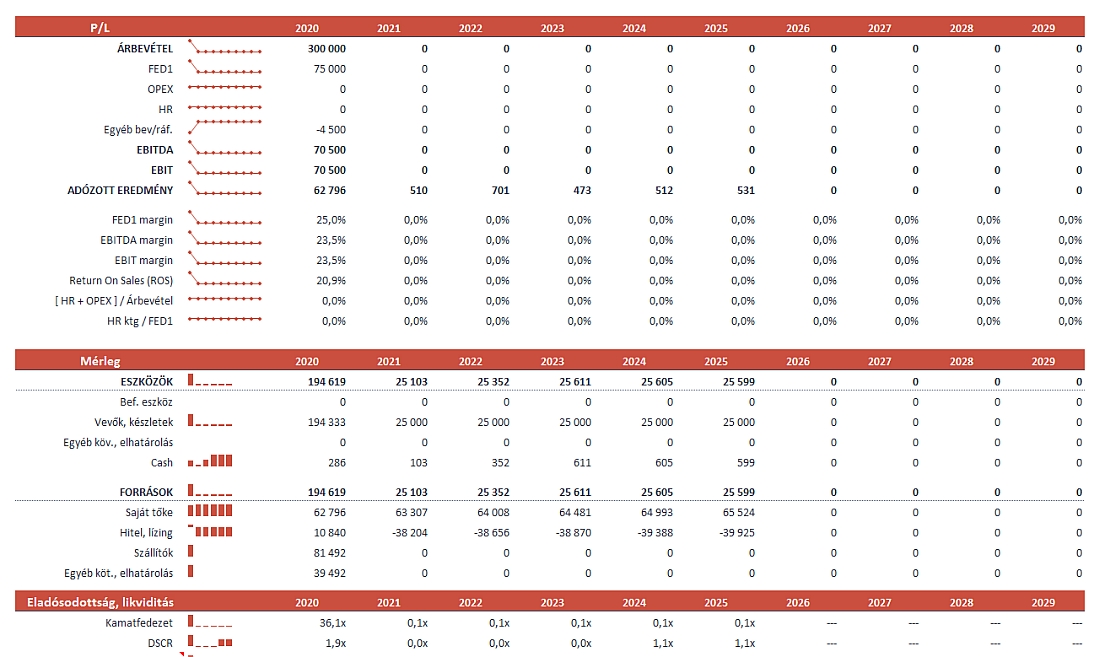
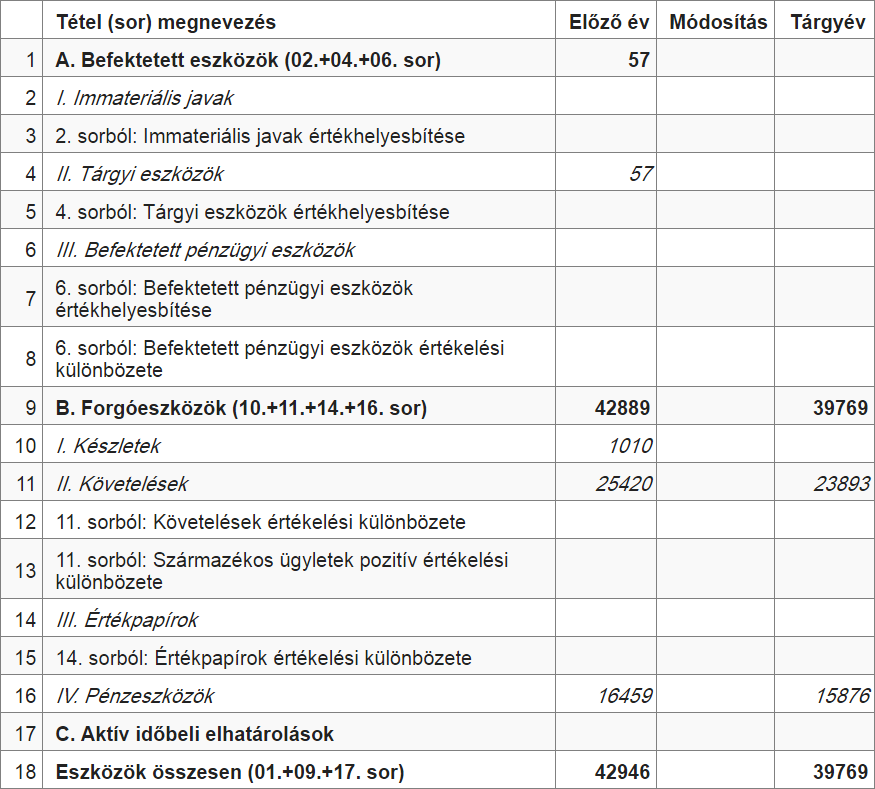
Pénzügyi Elemzés Minta: Egy Példa Vállalat Értékelése

Most nézzünk egy fiktív példát egy vállalat pénzügyi elemzésére. Tegyük fel, hogy rendelkezésünkre áll a “Alfa Kft.” 2023-as és 2024-es pénzügyi kimutatása.

Alfa Kft. – Mérleg (részlet)

Nernst Egyenlet Szamolas

A Nernst-egyenlet részletes számítása és alkalmazásai

Az elektrokémiában a Nernst-egyenlet központi szerepet tölt be az elektrokémiai cellák potenciáljának megértésében és kiszámításában olyan körülmények között, amelyek eltérnek a standard állapottól. Ez az egyenlet összekapcsolja egy elektród potenciálját az oldatban lévő ionok koncentrációjával és a hőmérséklettel. Mélyrehatóan megvizsgáljuk a Nernst-egyenlet matematikai alapjait, a benne szereplő paramétereket, a gyakorlati számítási módszereket és azokat a széleskörű alkalmazásokat, amelyek az elektrokémián túlmutatnak.

A Nernst-egyenlet elméleti háttere

A Nernst-egyenletet Walther Nernst német fizikus és kémikus dolgozta ki a 19. század végén. Az egyenlet termodinamikai alapokon nyugszik, és a Gibbs-szabadenergia változásával van szoros kapcsolatban egy elektrokémiai folyamat során. A standard elektródpotenciál (\\\(E^\\ominus\\\)) egy olyan referenciaérték, amelyet standard körülmények között (298 K hőmérséklet és 1 mol/dm³ koncentráció) mérnek. A Nernst-egyenlet lehetővé teszi számunkra, hogy meghatározzuk az elektródpotenciált (\\\(E\\\)) nem standard körülmények között, figyelembe véve a koncentráció és a hőmérséklet hatásait.

A Gibbs-szabadenergia és az elektrokémiai potenciál kapcsolata

A termodinamika második főtétele szerint egy spontán folyamat során a Gibbs-szabadenergia (\\\(\\Delta G\\\)) csökken. Egy elektrokémiai cellában a kémiai reakció által végzett elektromos munka közvetlenül arányos a Gibbs-szabadenergia változásával:

\\\(\\Delta G \= \-nFE\\\)

ahol:

• \\\(n\\\) az átvitt elektronok száma a cellareakcióban.

• \\\(F\\\) a Faraday-állandó (kb. \(96485 \, \text{C/mol}\)).
• \\\(E\\\) a cellapotenciál.

Standard körülmények között ez az összefüggés a következőképpen írható fel:

\\\(\\Delta G^\\ominus \= \-nFE^\\ominus\\\)

A Gibbs-szabadenergia változása egy általános kémiai reakcióra (\\\(aA \+ bB \\rightleftharpoons cC \+ dD\\\)) a következőképpen fejezhető ki:

\\\(\\Delta G \= \\Delta G^\\ominus \+ RT \\ln Q\\\)

ahol:

• \\\(R\\\) az egyetemes gázállandó (kb. \(8.314 \, \text{J/(mol·K)}\)).
• \\\(T\\\) a hőmérséklet Kelvinben.
• \\\(Q\\\) a reakcióhányados, amely a pillanatnyi koncentrációk vagy parciális nyomások hányadosa a reakció egyensúlyi állandójához hasonló formában.

Elektrokémiai cellákra alkalmazva, a reakcióhányados az ionok koncentrációjának függvénye. Az elektródreakciókra vonatkozóan a Nernst-egyenletet a fenti termodinamikai összefüggések kombinálásával vezethetjük le.

A Nernst-egyenlet levezetése

Tekintsünk egy általános redukciós félreakciót:

\\\(\\text\{Ox\} \+ ne^\- \\rightleftharpoons \\text\{Red\}\\\)

Ennek a félreakciónak a Gibbs-szabadenergia változása:

\\\(\\Delta G \= \\Delta G^\\ominus \+ RT \\ln \\frac\{a\_\{\\text\{Red\}\}\}\{a\_\{\\text\{Ox\}\}\}\}\\\)

ahol \(a_{\text{Red}}\) és \(a_{\text{Ox}}\) a redukált és oxidált formák aktivitásai. Híg oldatokban az aktivitásokat jó közelítéssel helyettesíthetjük a koncentrációkkal (\\\(\[\\text\{Red\}\]\\\) és \\\(\[\\text\{Ox\}\]\\\)).

Mivel \\\(\\Delta G \= \-nFE\\\) és \\\(\\Delta G^\\ominus \= \-nFE^\\ominus\\\), a fenti egyenlet a következőképpen írható át:

\\\(\-nFE \= \-nFE^\\ominus \+ RT \\ln \\frac\{\[\\text\{Red\}\]\}\{\[\\text\{Ox\}\]\}\}\\\)

Mindkét oldalt \(-nF\)-fel osztva megkapjuk a Nernst-egyenlet általános formáját:

\\\(E \= E^\\ominus \- \\frac\{RT\}\{nF\} \\ln \\frac\{\[\\text\{Red\}\]\}\{\[\\text\{Ox\}\]\}\}\\\)

Gyakran használják a természetes logaritmus helyett a 10-es alapú logaritmust is, ekkor az egyenlet a következőképpen alakul (298 K-en):

\\\(E \= E^\\ominus \- \\frac\{0\.0592 \\, \\text\{V\}\}\{n\} \\log\_\{10\} \\frac\{\[\\text\{Red\}\]\}\{\[\\text\{Ox\}\]\}\}\\\)

Ez az egyenlet kulcsfontosságú az elektrokémiai rendszerek viselkedésének megértéséhez nem standard körülmények között.

A Nernst-egyenlet komponensei és jelentésük

A Nernst-egyenlet különböző komponensei mind kritikus információt hordoznak az elektrokémiai folyamatról:

• \\\(E\\\): Az elektród potenciálja a megadott körülmények között (V).
• \\\(E^\\ominus\\\): A standard elektródpotenciál (V), amely standard körülmények között mért érték. Ezek az értékek táblázatokban találhatók meg.
• \\\(R\\\): Az egyetemes gázállandó (\\\(8\.314 \\, \\text\{J/\(mol·K\)\}\\\)).
• \\\(T\\\): A hőmérséklet Kelvinben (K).
• \\\(n\\\): Az átvitt elektronok száma a félreakcióban.
• \\\(F\\\): A Faraday-állandó (\\\(96485 \\, \\text\{C/mol\}\\\)).
• \\\(\[\\text\{Red\}\]\\\): A redukált forma koncentrációja (vagy aktivitása).
• \\\(\[\\text\{Ox\}\]\\\): Az oxidált forma koncentrációja (vagy aktivitása).

Mindegyik paraméter befolyásolja az elektród potenciálját, és ezáltal az elektrokémiai cella teljes feszültségét.

A standard elektródpotenciál (\\\(E^\\ominus\\\))

A standard elektródpotenciál egy relatív érték, amelyet a standard hidrogénelektródhoz (SHE) viszonyítva mérnek. A SHE potenciálját önkényesen nullának definiálták standard körülmények között (\\\(298 \\, \\text\{K\}\\\), \\\(1 \\, \\text\{atm\}\\\) nyomás a gázokra és \\\(1 \\, \\text\{mol/dm\}^3\\\) koncentráció az oldott anyagokra). A standard elektródpotenciál megadja egy adott félreakció hajlandóságát a redukcióra. Minél pozitívabb az \\\(E^\\ominus\\\) értéke, annál nagyobb a hajlandóság a redukcióra.

A hőmérséklet (\\\(T\\\)) hatása

A Nernst-egyenletben a hőmérséklet közvetlenül befolyásolja az elektród potenciálját. Általánosságban elmondható, hogy a hőmérséklet növekedésével az elektród potenciálja is változik, bár ennek mértéke függ a reakció természetétől és az ionok koncentrációjától. A hőmérséklet a termodinamikai tényezőket befolyásolja, amelyek meghatározzák az elektrokémiai egyensúlyt.

Az ionkoncentrációk hatása

Az ionok koncentrációja az \\\(\\frac\{\[\\text\{Red\}\]\}\{\[\\text\{Ox\}\]\}\\\) arányon keresztül jelenik meg a Nernst-egyenletben. Ha a redukált forma koncentrációja nő, vagy az oxidált forma koncentrációja csökken, az elektród potenciálja általában nő (azaz pozitívabbá válik a redukció szempontjából). Ennek intuitív magyarázata, hogy a magasabb redukált koncentráció vagy az alacsonyabb oxidált koncentráció elősegíti a redukciós folyamatot.

Az átvitt elektronok száma (\\\(n\\\))

Az átvitt elektronok száma (\\\(n\\\)) szintén fontos tényező a Nernst-egyenletben. Különböző félreakciók eltérő számú elektront vonhatnak be, ami befolyásolja, hogy az elektród potenciálja mennyire érzékeny a koncentrációváltozásokra.

A Nernst-egyenlet alkalmazása: Számítási példák

A Nernst-egyenlet gyakorlati alkalmazásának megértéséhez nézzünk néhány számítási példát.

Példa 1: Cink elektród potenciáljának számítása

Számítsuk ki a cink elektród potenciálját egy olyan oldatban, amelynek \\\(\[\\text\{Zn\}^\{2\+\}\]\\\) \= 0\.1 \\, \\text\{mol/dm\}^3 koncentrációjú, 298 K-en. A cink redukciós félreakciója és standard elektródpotenciálja a következő:

\\\(\\text\{Zn\}^\{2\+\}\(aq\) \+ 2e^\- \\rightleftharpoons \\text\{Zn\}\(s\) \\quad E^\\ominus \= \-0\.76 \\, \\text\{V\}\\\)

A Nernst-egyenlet erre a félreakcióra a következőképpen alakul:

\\\(E \= E^\\ominus \- \\frac\{0\.0592 \\, \\text\{V\}\}\{n\} \\log\_\{10\} \\frac\{\[\\text\{Zn\}\(s\)\]\}\{\[\\text\{Zn\}^\{2\+\}\(aq\)\]\}\}\\\)

Mivel a tiszta szilárd anyagok aktivitása egységnyi (\\\(\[\\text\{Zn\}\(s\)\] \= 1\\\)), az egyenlet tovább egyszerűsödik:

\\\(E \= E^\\ominus \- \\frac\{0\.0592 \\, \\text\{V\}\}\{2\} \\log\_\{10\} \\frac\{1\}\{\[\\text\{Zn\}^\{2\+\}\]\}\}\\\)

Behelyettesítve az értékeket:

\\\(E \= \-0\.76 \\, \\text\{V\} \- \\frac\{0\.0592 \\, \\text\{V\}\}\{2\} \\log\_\{10\} \\frac\{1\}\{0\.1\}\\\)

\\\(E \= \-0\.76 \\, \\text\{V\} \- 0\.0296 \\, \\text\{V\} \\log\_\{10\} \(10\)\\\)

\\\(E \= \-0\.76 \\, \\text\{V\} \- 0\.0296 \\, \\text\{V\} \\times 1\\\)

\\\(E \= \-0\.7896 \\, \\text\{V\}\\\)

Tehát a cink elektród potenciálja ebben az oldatban \(-0.7896 \, \text{V}\).

Példa 2: Réz elektród potenciáljának számítása eltérő hőmérsékleten

Számítsuk ki a réz elektród potenciálját egy olyan oldatban, amelynek \\\(\[\\text\{Cu\}^\{2\+\}\]\\\) \= 0\.01 \\, \\text\{mol/dm\}^3 koncentrációjú, 310 K-en. A réz redukciós félreakciója és standard elektródpotenciálja a következő:

\\\(\\text\{Cu\}^\{2\+\}\(aq\) \+ 2e^\- \\rightleftharpoons \\text\{Cu\}\(s\) \\quad E^\\ominus \= \+0\.34 \\, \\text\{V\}\\\)

Most a Nernst-egyenletet a természetes logaritmussal és a megadott hőmérséklettel használjuk:

\\\(E \= E^\\ominus \- \\frac\{RT\}\{nF\} \\ln \\frac\{1\}\{\[\\text\{Cu\}^\{2\+\}\]\}\}\\\)

Behelyettesítve az értékeket (\\\(R \= 8\.314 \\, \\text\{J/\(mol·K\)\}\\\), \\\(T \= 310 \\, \\text\{K\}\\\), \\\(n \= 2\\\), \\\(F \= 96485 \\, \\text\{C/mol\}\\\), \\\(\[\\text\{Cu\}^\{2\+\}\] \= 0\.01\\\)):

\\\(E \= 0\.34 \\, \\text\{V\} \- \\frac\{8\.314 \\, \\text\{J/\(mol·K\)\} \\times 310 \\, \\text\{K\}\}\{2 \\times 96485 \\, \\text\{C/mol\}\} \\ln \\frac\{1\}\{0\.01\}\\\)

\\\(E \= 0\.34 \\, \\text\{V\} \- \\frac\{2577\.34 \\, \\text\{J/mol\}\}\{192970 \\, \\text\{C/mol\}\} \\ln \(100\)\\\)

\\\(E \= 0\.34 \\, \\text\{V\} \- 0\.013356 \\, \\text\{V\} \\times 4\.605\\\)

\\\(E \= 0\.34 \\, \\text\{V\} \- 0\.0615 \\, \\text\{V\}\\\)

\\\(E \= 0\.2785 \\, \\text\{V\}\\\)

A réz elektród potenciálja ebben az esetben \(0.2785 \, \text{V}\).

Példa 3: Galvánelem potenciáljának számítása

Tekintsünk egy Daniell-elemet, amely cinkből és rézből áll:

\\\(\\text\{Zn\}\(s\) \| \\text\{Zn\}^\{2\+\}\(aq, 0\.05 \\, \\text\{M\}\) \|\| \\text\{Cu\}^\{2\+\}\(aq, 0\.5 \\, \\text\{M\}\) \| \\text\{Cu\}\(s\)\\\)

A katódon a redukció történik: \\\(\\text\{Cu\}^\{2\+\}\(aq\) \+ 2e^\- \\rightleftharpoons \\text\{Cu\}\(s\)\\\), \\\(E^\\ominus\_\{\\text\{Cu\}^\{2\+\}/\\text\{Cu\}\} \= \+0\.34 \\, \\text\{V\}\\\).

Az anódon az oxidáció történik: \\\(\\text\{Zn\}\(s\) \\rightleftharpoons \\text\{Zn\}^\{2\+\}\(aq\) \+ 2e^\-\\\), \\\(E^\\ominus\_\{\\text\{Zn\}^\{2\+\}/\\text\{Zn\}\} \= \-0\.76 \\, \\text\{V\}\\\).

Először számítsuk ki az egyes elektródok potenciálját a Nernst-egyenlettel (298 K-en).

A katód potenciálja:

$$\(E_{\text{katód}} = E^\ominus_{\text{Cu}^{2+}/\text{Cu}} – \frac{0.0592 \, \text{V}}{2} \log_{10} \frac{1}{[\text{

Hatasfok Feladatok Megoldassal

A Hatásfok Részletes Tanulmánya: Feladatok és Kimerítő Megoldások

Üdvözöljük a hatásfok átfogó útmutatójában! Célunk, hogy ezen a részletes oldalon keresztül minden olvasó számára érthetővé és elsajátíthatóvá tegyük a hatásfok fogalmát, annak alkalmazási területeit, valamint a hozzá kapcsolódó feladatok megoldásának módszereit. Legyen szó fizikát tanuló diákról, mérnöki hallgatóról vagy bárkiről, aki érdeklődik a hatékonyság és az energiaátalakítások iránt, itt mindent megtalál, amire szüksége lehet.

Mi is pontosan a Hatásfok?

A hatásfok egy alapvető fogalom a természettudományokban és a mérnöki tudományokban, amely egy adott folyamat vagy eszköz hatékonyságát méri. Meghatározása szerint a hasznos kimenet és a befektetett bemenet aránya. Gyakran százalékban fejezzük ki, megmutatva, hogy a befektetett energia vagy munka mekkora része alakul át a kívánt formában. Egy ideális rendszerben a hatásfok 100% lenne, ami azt jelentené, hogy a teljes befektetett energia hasznos munkává alakul át veszteség nélkül. A valóságban azonban minden folyamat során fellépnek veszteségek, így a hatásfok mindig kisebb, mint 100%.

A Hatásfok Matematikai Kifejezése

A hatásfok ($\eta$) matematikailag a következőképpen fejezhető ki:

$$\eta = \frac{\text{Hasznos kimenet}}{\text{Befektetett bemenet}}$$

Ha a hatásfokot százalékban szeretnénk megkapni, akkor a fenti képlet eredményét meg kell szoroznunk 100-zal:

$$\eta\% = \frac{\text{Hasznos kimenet}}{\text{Befektetett bemenet}} \times 100\%$$

Ahol a “hasznos kimenet” lehet például elvégzett munka, leadott energia vagy egy adott feladat eléréséhez szükséges eredmény, a “befektetett bemenet” pedig az a teljes energia vagy munka, amelyet a folyamatba fektettünk.

A Hatásfok Fontossága és Alkalmazási Területei

A hatásfok ismerete és optimalizálása kulcsfontosságú számos területen. A mérnöki tervezés során elengedhetetlen a hatékony rendszerek létrehozása, legyen szó erőművekről, gépekről vagy elektronikai eszközökről. A magasabb hatásfok kevesebb energiaveszteséget jelent, ami gazdasági és környezetvédelmi szempontból is előnyös. A mindennapi életben is találkozhatunk a hatásfok fogalmával, például egy háztartási gép energiahatékonyságának értékelésekor.

Alkalmazási területek részletesen:

Energetika

Az energetikában a hatásfok kiemelkedően fontos. Az erőművek célja, hogy a rendelkezésre álló energiaforrásokat (például fosszilis tüzelőanyagok, nukleáris energia, vízenergia, szélenergia, napenergia) minél hatékonyabban alakítsák át elektromos energiává. Egy erőmű hatásfoka megmutatja, hogy a felhasznált energia mekkora hányada alakul át elektromos árammá. A veszteségek leggyakrabban hő formájában jelentkeznek. A kutatások és fejlesztések folyamatosan arra irányulnak, hogy növeljék az erőművek hatásfokát, ezáltal csökkentve az erőforrás-igényt és a környezeti terhelést.

Gépészet

A gépészet területén a gépek és berendezések hatásfoka kritikus fontosságú. Egy motor, egy szivattyú vagy egy hűtőgép esetében a hatásfok azt mutatja meg, hogy a befektetett energia (elektromos áram, üzemanyag) mekkora része alakul át hasznos munkává (forgatónyomaték, folyadékszállítás, hűtés). A magasabb hatásfok alacsonyabb energiafogyasztást és ezáltal alacsonyabb üzemeltetési költségeket eredményez. A gépészeti tervezés során a cél a minél magasabb hatásfokú alkatrészek és rendszerek kifejlesztése.

Elektronika

Az elektronikában az áramkörök és az elektronikai eszközök hatásfoka befolyásolja az energiafogyasztást és a hőtermelést. Egy tápegység hatásfoka például azt mutatja meg, hogy a bemeneti elektromos energia mekkora része jut el a kimenetre a kívánt formában. Az alacsony hatásfokú tápegységek jelentős mennyiségű energiát alakíthatnak át hővé, ami nemcsak energiaveszteséget jelent, hanem hűtési problémákat is okozhat. A modern elektronikai eszközök tervezésénél nagy hangsúlyt fektetnek a magas hatásfokú alkatrészek és áramkörök alkalmazására.

Közlekedés

A közlekedési eszközök, mint például autók, vonatok és repülők hatásfoka közvetlenül befolyásolja az üzemanyag-fogyasztást és a károsanyag-kibocsátást. Egy belsőégésű motor hatásfoka azt mutatja meg, hogy az üzemanyagban tárolt kémiai energia mekkora része alakul át mechanikai munkává a kerekek hajtására. Az elektromos járművek hajtásláncának hatásfoka pedig az elektromos energia mechanikai energiává alakításának hatékonyságát jelzi. A magasabb hatásfokú járművek kevesebb üzemanyagot fogyasztanak vagy hosszabb távot tudnak megtenni egy töltéssel.

A Hatásfok Számításának Lépései

A hatásfok kiszámításához a következő lépéseket kell követnünk:

1. Határozzuk meg a hasznos kimenetet. Ez lehet munka, energia vagy bármilyen más kívánt eredmény, amelyet a rendszer produkál.
2. Határozzuk meg a befektetett bemenetet. Ez az a teljes energia vagy munka, amelyet a rendszerbe bevezetünk a kívánt kimenet elérése érdekében.
3. Osszuk el a hasznos kimenetet a befektetett bemenettel.
4. Ha a hatásfokot százalékban szeretnénk megkapni, szorozzuk meg az eredményt 100-zal.

Gyakorlati Feladatok a Hatásfok Számításához Megoldásokkal

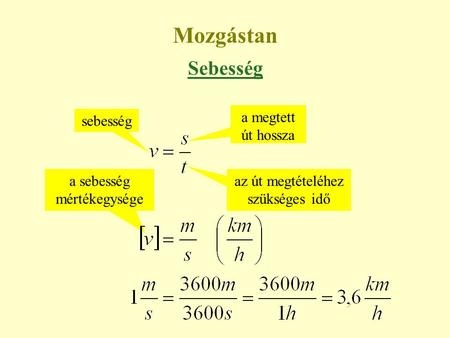
Most nézzünk meg néhány gyakorlati feladatot, amelyek segítenek megérteni a hatásfok számításának folyamatát.

1. feladat: Elektromos motor hatásfoka

Egy elektromos motor 1000 J elektromos energiát vesz fel, és ennek hatására 800 J mechanikai munkát végez. Számítsa ki a motor hatásfokát!

Befektetett bemenet (elektromos energia) = 1000 J

Hasznos kimenet (mechanikai munka) = 800 J

A hatásfok ($\eta$) képlete:

$$\eta = \frac{\text{Hasznos kimenet}}{\text{Befektetett bemenet}}$$

Behelyettesítve az értékeket:

$$\eta = \frac{800 \text{ J}}{1000 \text{ J}} = 0.8$$

Százalékban kifejezve:

$$\eta\% = 0.8 \times 100\% = 80\%$$

A motor hatásfoka 80%.

2. feladat: Fűtőberendezés hatásfoka

Egy elektromos fűtőberendezés 5000 J elektromos energiát fogyaszt, és ennek hatására 4500 J hőenergiát ad le. Mekkora a fűtőberendezés hatásfoka?

Befektetett bemenet (elektromos energia) = 5000 J

Hasznos kimenet (hőenergia) = 4500 J

A hatásfok ($\eta$) képlete:

$$\eta = \frac{\text{Hasznos kimenet}}{\text{Befektetett bemenet}}$$

Behelyettesítve az értékeket:

$$\eta = \frac{4500 \text{ J}}{5000 \text{ J}} = 0.9$$

Százalékban kifejezve:

$$\eta\% = 0.9 \times 100\% = 90\%$$

A fűtőberendezés hatásfoka 90%.

3. feladat: Biciklizés hatásfoka

Egy biciklis 10000 J kémiai energiát éget el a szervezetében, és ennek hatására 2000 J mechanikai munkát végez a bicikli pedáljainak forgatásával. Számítsa ki a biciklis “hatásfokát” ebben a folyamatban!

Befektetett bemenet (kémiai energia) = 10000 J

Hasznos kimenet (mechanikai munka) = 2000 J

A hatásfok ($\eta$) képlete:

$$\eta = \frac{\text{Hasznos kimenet}}{\text{Befektetett bemenet}}$$

Behelyettesítve az értékeket:

$$\eta = \frac{2000 \text{ J}}{10000 \text{ J}} = 0.2$$

Százalékban kifejezve:

$$\eta\% = 0.2 \times 100\% = 20\%$$

A biciklizés “hatásfoka” 20%.

Komplexebb Hatásfok Feladatok és Megoldásaik

Most nézzünk meg néhány összetettebb feladatot, amelyek több lépést vagy több fogalom együttes alkalmazását igénylik.

4. feladat: Erőmű hatásfoka

Egy szénerőmű 10 MJ (megajoule) kémiai energiát alakít át elektromos energiává. A termelt elektromos energia mennyisége 3.5 MJ. Számítsa ki az erőmű hatásfokát!

Befektetett bemenet (kémiai energia) = 10 MJ = 10,000,000 J

Hasznos kimenet (elektromos energia) = 3.5 MJ = 3,500,000 J

A hatásfok ($\eta$) képlete:

$$\eta = \frac{\text{Hasznos kimenet}}{\text{Befektetett bemenet}}$$

Behelyettesítve az értékeket:

$$\eta = \frac{3,500,000 \text{ J}}{10,000,000 \text{ J}} = 0.35$$

Százalékban kifejezve:

$$\eta\% = 0.35 \times 100\% = 35\%$$

Az erőmű hatásfoka 35%.

5. feladat: Két lépcsős energiaátalakítás

Egy napelem 1000 J napenergiát nyel el, és 200 J elektromos energiát termel. Ezt az elektromos energiát egy motor hajtja meg, amely 80%-os hatásfokkal működik. Mennyi mechanikai munkát végez a motor?

Először számítsuk ki a napelem hatásfokát:

$$\eta_{\text{napelem}} = \frac{200 \text{ J}}{1000 \text{ J}} = 0.2 = 20\%$$

A motorba jutó elektromos energia 200 J. A motor hatásfoka 80%, ami azt jelenti, hogy az elektromos energia 80%-a alakul át mechanikai munkává.

Mechanikai munka = Befektetett elektromos energia $\times$ Motor hatásfoka

Mechanikai munka = 200 \text{ J} \times 0.8 = 160 \text{ J}

A motor 160 J mechanikai munkát végez.

6. feladat: Szivattyú hatásfoka

Egy szivattyú 500 W teljesítményű elektromos motorral működik. A szivattyú 10 liter vizet emel fel 5 méter magasra 10 másodperc alatt. Számítsa ki a szivattyú rendszerének hatásfokát! (A víz sűrűsége $\rho = 1000 \, \text{kg/m}^3$, a gravitációs gyorsulás $g = 9.8 \, \text{m/s}^2$).

Először számítsuk ki a befektetett elektromos energiát: