Munka Energia Teljesitmeny Feladatok Megoldassal
A Munka, Energia és Teljesítmény Világa: Átfogó Útmutató Feladatokkal és Részletes Megoldásokkal
Ebben a kimerítő cikkben mélyrehatóan feltárjuk a munka, az energia és a teljesítmény alapvető fogalmait a fizikában. Nem csupán definíciókkal szolgálunk, hanem részletes magyarázatokon keresztül vezetjük végig Olvasóinkat, illusztratív példákkal és gondosan kidolgozott feladatokkal segítve a megértést. Célunk, hogy Ön ne csak elsajátítsa ezeket a kulcsfontosságú fizikai elveket, hanem képes legyen azokat magabiztosan alkalmazni a legkülönfélébb problémák megoldása során.
A Munka Fogalma a Fizikában: Több, Mint Pusztán Fáradozás
A hétköznapi nyelvhasználattól eltérően a fizikában a munka egy precízen definiált fogalom. Akkor végzünk munkát egy testtel, ha egy erő hatására a test elmozdul az erő irányában (vagy az erő elmozdulás irányú komponense mentén). Matematikailag a munka (W) a testre ható erő (\\mathbf\{F\}) és az elmozdulás (\\mathbf\{d\}) skaláris szorzataként definiálható:
\\mathbf\{W\} \= \\mathbf\{F\} \\cdot \\mathbf\{d\} \= \|\\mathbf\{F\}\| \|\\mathbf\{d\}\| \\cos \\theta
ahol \|\\mathbf\{F\}\| az erő nagysága, \|\\mathbf\{d\}\| az elmozdulás nagysága, és \\theta az erő és az elmozdulás közötti szög. A munka mértékegysége a Joule (J), amely megegyezik az 1 Newton szorozva 1 méterrel (1 N⋅m).
Példa a Munka Számítására
Képzeljünk el egy esetet, ahol egy 10 N nagyságú vízszintes erővel eltolunk egy dobozt 5 méteren keresztül egy vízszintes felületen. Mivel az erő és az elmozdulás azonos irányú, a \\cos \\theta \= \\cos 0^\\circ \= 1. Így a végzett munka:
W \= \(10 \\, \\text\{N\}\) \\times \(5 \\, \\text\{m\}\) \\times 1 \= 50 \\, \\text\{J\}
Feladat 1: Munkavégzés Ferde Erővel
Egy 2 kg tömegű testet egy vízszintes felületen húzunk egy 20 N nagyságú erővel, amely a vízszintessel 30 fokos szöget zár be. Mekkora munkát végzünk, ha a test 3 métert mozdul el?
Megoldás:
Az erő vízszintes komponense F\_x \= \|\\mathbf\{F\}\| \\cos \\theta \= 20 \\, \\text\{N\} \\times \\cos 30^\\circ \= 20 \\, \\text\{N\} \\times \\frac\{\\sqrt\{3\}\}\{2\} \\approx 17\.32 \\, \\text\{N\}.
A végzett munka W \= F\_x \\times d \= 17\.32 \\, \\text\{N\} \\times 3 \\, \\text\{m\} \\approx 51\.96 \\, \\text\{J\}.
Az Energia Sokszínű Formái: A Munkavégzés Lehetősége

Az energia egy test vagy rendszer azon képessége, hogy munkát végezzen. Számos formában létezik, beleértve a kinetikus energiát (mozgás energiája), a potenciális energiát (helyzetből vagy állapotból származó energia), a termikus energiát (hő), a kémiai energiát, a nukleáris energiát és a sugárzási energiát. Az energia mértékegysége szintén a Joule (J).
Kinetikus Energia: A Mozgásban Rejlő Erő
Egy m tömegű, v sebességgel mozgó test kinetikus energiája (K) a következőképpen számítható:
K \= \\frac\{1\}\{2\} m v^2
Minél nagyobb a test tömege vagy sebessége, annál nagyobb a kinetikus energiája, és annál több munkát képes végezni a megállásáig.
Potenciális Energia: A Helyzetből Adódó Lehetőség
A potenciális energia egy test helyzetéből vagy konfigurációjából adódik. A leggyakrabban tárgyalt formái a gravitációs potenciális energia és a rugalmas potenciális energia.
Gravitációs Potenciális Energia
Egy m tömegű testnek a Föld felszínétől h magasságban lévő gravitációs potenciális energiája (U\_g) a következőképpen adható meg:
U\_g \= mgh
ahol g a gravitációs gyorsulás (kb. 9\.81 \\, \\text\{m/s\}^2 a Föld felszínén).
Rugalmas Potenciális Energia
Egy k rugóállandójú rugóban, amely x méterrel van megnyújtva vagy összenyomva, tárolt rugalmas potenciális energia (U\_e) a következőképpen számítható:
U\_e \= \\frac\{1\}\{2\} k x^2
Feladat 2: Kinetikus és Potenciális Energia
Egy 0.5 kg tömegű labdát 10 m/s sebességgel függőlegesen feldobunk a földről. Mekkora a labda kinetikus energiája a feldobás pillanatában? Mekkora a gravitációs potenciális energiája a legmagasabb ponton, ha a légellenállást elhanyagoljuk?
Megoldás:
A feldobás pillanatában a kinetikus energia: K \= \\frac\{1\}\{2\} \(0\.5 \\, \\text\{kg\}\) \(10 \\, \\text\{m/s\}\)^2 \= 25 \\, \\text\{J\}.
A legmagasabb ponton a kinetikus energia nulla (a labda pillanatnyi sebessége nulla). Az összes kezdeti kinetikus energia gravitációs potenciális energiává alakul. Így a legmagasabb ponton a potenciális energia is 25 J.
A Munkatétel: Kapocs a Munka és az Energia Között
A munkatétel egy alapvető elv a mechanikában, amely kimondja, hogy egy testre ható összes erő által végzett nettó munka egyenlő a test kinetikus energiájának megváltozásával:
W\_\{netto\} \= \\Delta K \= K\_f \- K\_i \= \\frac\{1\}\{2\} m v\_f^2 \- \\frac\{1\}\{2\} m v\_i^2
Ez a tétel rendkívül hasznos a mozgás elemzésében, különösen akkor, ha az erők nem állandóak.
Feladat 3: A Munkatétel Alkalmazása
Egy 1000 kg tömegű autó álló helyzetből indul, és egy állandó eredő erő hatására 20 m/s sebességet ér el 100 méter megtétele után. Mekkora volt az eredő erő?
Megoldás:
A kinetikus energia megváltozása: \\Delta K \= \\frac\{1\}\{2\} \(1000 \\, \\text\{kg\}\) \(20 \\, \\text\{m/s\}\)^2 \- \\frac\{1\}\{2\} \(1000 \\, \\text\{kg\}\) \(0 \\, \\text\{m/s\}\)^2 \= 200000 \\, \\text\{J\}.
A munkatétel szerint W\_\{netto\} \= \\Delta K, így F\_\{netto\} \\times d \= 200000 \\, \\text\{J\}.
Az eredő erő F\_\{netto\} \= \\frac\{200000 \\, \\text\{J\}\}\{100 \\, \\text\{m\}\} \= 2000 \\, \\text\{N\}.
Az Energia Megmaradásának Törvénye: Egyetemes Elv
Az energia megmaradásának törvénye az egyik legalapvetőbb és legszélesebb körben érvényesülő természeti törvény. Kimondja, hogy egy zárt rendszer teljes energiája állandó marad az időben. Az energia átalakulhat egyik formából a másikba, de nem keletkezhet és nem veszhet el.
Példa az Energia Megmaradására
Egy inga lengése során a gravitációs potenciális energia folyamatosan kinetikus energiává alakul, amikor az inga lefelé mozog, és fordítva, a kinetikus energia potenciális energiává alakul, amikor az inga felfelé lendül. Ha elhanyagoljuk a súrlódást és a légellenállást, a rendszer mechanikai energiája (a kinetikus és potenciális energia összege) állandó marad.
Feladat 4: Energia Megmaradás Inga Esetén
Egy 1 kg tömegű inga 1 méter hosszú fonálon lóg. Az ingát vízszintes helyzetből elengedjük. Mekkora lesz az inga sebessége a legalsó ponton?
Megoldás:
A kezdeti helyzetben az ingának csak gravitációs potenciális energiája van a legalsó ponthoz képest: U\_i \= mgh \= \(1 \\, \\text\{kg\}\) \(9\.81 \\, \\text\{m/s\}^2\) \(1 \\, \\text\{m\}\) \= 9\.81 \\, \\text\{J\}. A kezdeti kinetikus energia nulla.

A legalsó ponton a gravitációs potenciális energia nulla, és az összes kezdeti potenciális energia kinetikus energiává alakul: K\_f \= \\frac\{1\}\{2\} m v\_f^2.
Az energia megmaradásának törvénye szerint U\_i \= K\_f, így 9\.81 \\, \\text\{J\} \= \\frac\{1\}\{2\} \(1 \\, \\text\{kg\}\) v\_f^2.
Ebből a sebesség v\_f \= \\sqrt\{\\frac\{2 \\times 9\.81 \\, \\text\{J\}\}\{1 \\, \\text\{kg\}\}\} \\approx 4\.43 \\, \\text\{m/s\}.

A Teljesítmény Fogalma: A Munkavégzés Sebessége
A teljesítmény (P) azt adja meg, hogy milyen gyorsan végeznek munkát, vagy milyen gyorsan alakul át az energia. Matematikailag a teljesítmény a végzett munka és az eltelt idő hányadosa:
P \= \\frac\{W\}\{t\}
A teljesítményt az energia idő szerinti deriváltjaként is definiálhatjuk:
P \= \\frac\{dE\}\{dt\}
A teljesítmény mértékegysége a Watt (W), amely megegyezik az 1 Joule per másodperccel (1 J/s).

Teljesítmény Állandó Erő Esetén
Ha egy állandó \\mathbf\{F\} erő egy testet \\mathbf\{v\} sebességgel mozgat, akkor a teljesítmény:

P \= \\mathbf\{F\} \\cdot \\mathbf\{v\} \= \|\\mathbf\{F\}\| \|\\mathbf\{v\}\| \\cos \\phi
ahol \\phi az erő és a sebesség közötti szög.
Feladat 5: Teljesítmény Számítása
Egy daru egy 500 kg tömegű terhet 10 méter magasra emel fel 20 másodperc alatt állandó sebességgel. Mekkora a daru által kifejtett átlagos teljesítmény?
Megoldás:
A daru által végzett munka a gravitáció ellenében: W \= mgh \= \(500 \\, \\text\{kg\}\) \(9\.81 \\, \\text\{m/s\}^2\) \(10 \\, \\text\{m\}\) \= 49050 \\, \\text\{J\}.
Az átlagos teljesítmény: P \= \\frac\{W\}\{t\} \= \\frac\{49050 \\, \\text\{J\}\}\{20 \\, \\text\{s\}\} \= 2452\.5 \\, \\text\{W\}.
A Hatásfok: A Hasznos Munkavégzés Mértéke
A valóságban az energiaátalakítások sosem tökéletesek; mindig van valamennyi energiaveszteség, leggyakrabban hő formájában. A hatásfok (\\eta) azt adja meg, hogy egy rendszer a befektetett energiának vagy munkának mekkora hányadát képes hasznos munkává vagy energiává alakítani:
\\eta \= \\frac\{W\_\{hasznos\}\}\{W\_\{befektetett\}\} \= \\frac\{E\_\{hasznos\}\}\{E\_\{befektetett\}\}
A hatásfok mindig 0 és 1 (vagy 0% és 100%) közötti érték.
Példa a Hatásfokra
Egy elektromos motor 1000 J elektromos energiát vesz fel, és ennek hatására 800 J mechanikai munkát végez. A motor hatásfoka \\eta \= \\frac\{800 \\, \\text\{J\}\}\{1000 \\, \\text\{J\}\} \= 0\.8, vagyis 80%.
Feladat 6: Hatásfok Számítása
Egy benzinmotor 50000 J kémiai energiát alakít át, miközben 12500 J mechanikai munkát végez. Mekkora a motor hatásfoka?
Megoldás:
A motor hatásfoka: \\eta \= \\frac\{12500 \\, \\text\{J\}\}\{50000 \\, \\text\{J\}\} \= 0\.25, vagyis 25%.
További Összetett Feladatok a Munka, Energia és Teljesítmény Témakörében
Összetett Feladat 1: Lejtőn Csúszó Test
Egy 5 kg tömegű test egy 30

Mechanikai Energia Megmaradas Torvenye
A Mechanikai Energia Megmaradásának Törvénye: A Fizika Egyik Alapköve
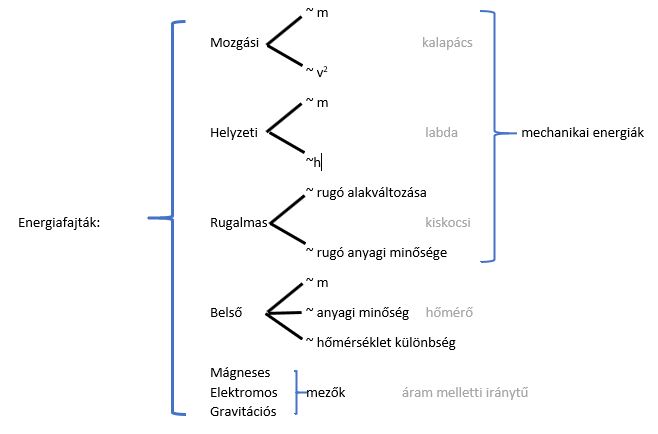
A mechanikai energia megmaradásának törvénye a fizika egyik legfontosabb és legszélesebb körben alkalmazható alapelve. Kimondja, hogy egy izolált rendszerben, ahol csak konzervatív erők (mint például a gravitációs erő vagy a rugalmas erő) hatnak, a mechanikai energia – vagyis a kinetikus energia és a potenciális energia összege – időben állandó marad. Ez azt jelenti, hogy az energia nem vész el, hanem csak átalakul egyik formájából a másikba. Ebben a részletes cikkben mélyrehatóan megvizsgáljuk ezt a fundamentális törvényt, feltárjuk a mögötte rejlő elveket, szemléletes példákon keresztül mutatjuk be alkalmazásait, és megvitatjuk a nem konzervatív erők hatását is.
A Mechanikai Energia Definíciója és Összetevői
A mechanikai energia egy rendszer azon képessége, hogy munkát végezzen a mozgása vagy a helyzete miatt. Két fő összetevője van: a kinetikus energia és a potenciális energia. Ahhoz, hogy teljes mértékben megértsük a mechanikai energia megmaradásának törvényét, elengedhetetlen, hogy tisztában legyünk ezen összetevők definíciójával és jelentésével.
A Kinetikus Energia: A Mozgás Energiája
A kinetikus energia egy test mozgásából származó energia. Minél nagyobb egy test tömege és minél gyorsabban mozog, annál nagyobb a kinetikus energiája. Matematikailag a kinetikus energia (E\_k) a következőképpen fejezhető ki:
\\mathbf\{E\_k \= \\frac\{1\}\{2\}mv^2\}
ahol \\mathbf\{m\} a test tömege, \\mathbf\{v\} pedig a sebessége. Ebből az egyenletből is látható, hogy a kinetikus energia négyzetesen függ a sebességtől, ami azt jelenti, hogy a sebesség kétszeresére növelése négyszeresére növeli a kinetikus energiát. A tömeggel pedig egyenesen arányos, tehát kétszer akkora tömeg kétszer akkora kinetikus energiát jelent azonos sebesség mellett.
Gondoljunk csak egy guruló labdára, egy repülő repülőgépre vagy egy futó emberre. Mindegyik rendelkezik kinetikus energiával a mozgásuk miatt. Minél gyorsabban mozognak, annál nagyobb ez az energia. A kinetikus energia kulcsszerepet játszik számos fizikai jelenség megértésében, a mikroszkopikus részecskék mozgásától kezdve a bolygók pályájáig.
A Potenciális Energia: A Helyzetből Származó Energia
A potenciális energia egy test helyzetéből vagy konfigurációjából származó tárolt energia. Többféle formája létezik, attól függően, hogy milyen erőhatás eredményezi ezt az energiát. A mechanikában leggyakrabban a gravitációs potenciális energiával és a rugalmas potenciális energiával találkozunk.
Gravitációs Potenciális Energia
A gravitációs potenciális energia egy testnek a gravitációs térben elfoglalt helyzetéből adódik. A Föld felszínén, egy \\mathbf\{h\} magasságban lévő \\mathbf\{m\} tömegű test gravitációs potenciális energiája (E\_p) a következőképpen számítható ki:
\\mathbf\{E\_p \= mgh\}
ahol \\mathbf\{g\} a gravitációs gyorsulás (a Földön megközelítőleg 9\.81 \\, m/s^2). Ebből az egyenletből láthatjuk, hogy minél magasabbra emelünk egy testet, annál nagyobb lesz a gravitációs potenciális energiája. Ez az energia akkor szabadul fel, amikor a test leesik, és a potenciális energia kinetikus energiává alakul át.
Például egy hegy tetején álló kő nagyobb gravitációs potenciális energiával rendelkezik, mint egy a völgyben fekvő kő. Amikor a kő legurul a hegyről, ez a potenciális energia fokozatosan kinetikus energiává alakul át, miközben a magassága csökken.
Rugalmas Potenciális Energia
A rugalmas potenciális energia egy rugalmasan deformálható testben (például egy megnyújtott rugóban vagy egy meghajlított íjban) tárolt energia. Ha egy rugót \\mathbf\{x\} távolsággal megnyújtunk vagy összenyomunk a nyugalmi helyzetéhez képest, a benne tárolt rugalmas potenciális energia (E\_\{pr\}) a következőképpen adható meg:

\\mathbf\{E\_\{pr\} \= \\frac\{1\}\{2\}kx^2\}
ahol \\mathbf\{k\} a rugóállandó, amely a rugó merevségét jellemzi. Minél nagyobb a rugóállandó vagy a deformáció mértéke, annál nagyobb a tárolt rugalmas potenciális energia.
Egy megfeszített íjban tárolt rugalmas potenciális energia például arra használható fel, hogy egy nyilat nagy sebességgel kilőjön. Amikor az íj elengedik, a rugalmas potenciális energia kinetikus energiává alakul át, ami a nyilat repíti.
A Mechanikai Energia Megmaradásának Törvénye: A Kimondás és Magyarázat
Most, hogy megértettük a kinetikus és a potenciális energia fogalmát, rátérhetünk a mechanikai energia megmaradásának törvényére. Ahogy korábban említettük, ez a törvény azt állítja, hogy egy olyan izolált rendszerben, amelyre csak konzervatív erők hatnak, a mechanikai energia (a kinetikus és potenciális energia összege) állandó marad.
Matematikailag ezt a következőképpen fejezhetjük ki:
\\mathbf\{E\_\{mech\} \= E\_k \+ E\_p \= állandó\}
Vagyis, ha egy rendszer kezdeti állapotában a kinetikus energia E\_\{k1\} és a potenciális energia E\_\{p1\}, a mechanikai energia E\_\{mech1\} \= E\_\{k1\} \+ E\_\{p1\}. Egy későbbi időpontban, ha a kinetikus energia E\_\{k2\} és a potenciális energia E\_\{p2\}, akkor a mechanikai energia E\_\{mech2\} \= E\_\{k2\} \+ E\_\{p2\}. A megmaradás törvénye szerint:
\\mathbf\{E\_\{mech1\} \= E\_\{mech2\}\}
\\mathbf\{E\_\{k1\} \+ E\_\{p1\} \= E\_\{k2\} \+ E\_\{p2\}\}
Ez az egyenlet rendkívül hasznos problémák megoldásában, ahol energiatranszformációk történnek, de nincsenek nem konzervatív erők, amelyek energiát vonhatnak el a rendszerből (például súrlódás vagy légellenállás).
Konzervatív Erők vs. Nem Konzervatív Erők
A mechanikai energia megmaradásának törvénye szigorúan csak olyan rendszerekre érvényes, ahol a ható erők konzervatívak. Fontos megérteni a különbséget a konzervatív és a nem konzervatív erők között.
Konzervatív Erők
Egy erő akkor konzervatív, ha az általa végzett munka egy zárt úton nulla, vagy ha a két pont közötti munka független az úttól. A mechanikában a leggyakoribb konzervatív erők a gravitációs erő és a rugalmas erő. Amikor egy konzervatív erő munkát végez egy rendszeren, az energia potenciális energiaként tárolódik, és később visszanyerhető kinetikus energiaként (vagy más formában).
- Gravitációs erő: A gravitációs erő által végzett munka egy test felemelésekor megegyezik a gravitációs potenciális energia növekedésével. Amikor a test leesik, ez a potenciális energia kinetikus energiává alakul vissza.
- Rugalmas erő: Egy rugó megnyújtásakor vagy összenyomásakor a rugalmas erő munkát végez, amely rugalmas potenciális energiaként tárolódik. Amikor a rugó visszatér nyugalmi helyzetébe, ez az energia kinetikus energiává alakulhat.

Nem Konzervatív Erők
Egy erő akkor nem konzervatív, ha az általa végzett munka függ az úttól, és nem nulla egy zárt úton. A mechanikában a leggyakoribb nem konzervatív erők a súrlódási erő és a légellenállás. Amikor egy nem konzervatív erő munkát végez, az energia általában hővé alakul, és nem tér vissza a rendszer mechanikai energiájába.

- Súrlódási erő: Ha egy test egy felületen csúszik, a súrlódási erő munkát végez, amely hővé alakítja a mechanikai energiát (mind a test, mind a felület felmelegszik). Ez az energia nem nyerhető vissza mechanikai munkaként a rendszerben.
- Légellenállás: Egy levegőben mozgó testre ható légellenállási erő szintén nem konzervatív. Munkája hővé alakítja a mechanikai energiát és a levegő áramlásának energiájává.

A mechanikai energia megmaradásának törvénye csak akkor alkalmazható közvetlenül, ha a rendszerben ható összes erő konzervatív. Ha nem konzervatív erők is jelen vannak, akkor a rendszer teljes energiája (beleértve a hőenergiát is) marad meg, de a mechanikai energia önmagában nem feltétlenül állandó.
Példák a Mechanikai Energia Megmaradására
Számos klasszikus példa illusztrálja a mechanikai energia megmaradásának törvényét a gyakorlatban. Nézzünk meg néhányat részletesen:
Egy Szabadon Eső Test
Képzeljünk el egy \\mathbf\{m\} tömegű testet, amelyet egy \\mathbf\{h\} magasságból elejtünk. Kezdetben a test nyugalomban van, így a kinetikus energiája nulla (E\_\{k1\} \= 0), a potenciális energiája pedig E\_\{p1\} \= mgh. Tehát a kezdeti mechanikai energia E\_\{mech1\} \= 0 \+ mgh \= mgh.
Amint a test esni kezd, a gravitációs erő munkát végez rajta, és a potenciális energiája csökken, miközben a sebessége és ezzel együtt a kinetikus energiája nő. Egy tetszőleges \\mathbf\{y\} magasságban (ahol 0 \\le y \\le h), a potenciális energia E\_\{p2\} \= mgy. A sebességet ebben a pontban a következőképpen számíthatjuk ki a mozgásegyenletekből:
v^2 \= v\_0^2 \+ 2a\(h\-y\)

Mivel a kezdeti sebesség v\_0 \= 0 és a gyorsulás a \= g, ezért:
v^2 \= 2g\(h\-y\)
Így a kinetikus energia ebben a pontban:
E\_\{k2\} \= \\frac\{1\}\{2\}mv^2 \= \\frac\{1\}\{2\}m\(2g\(h\-y\)\) \= mg\(h\-y\)
A mechanikai energia ezen a ponton tehát:
E\_\{mech2\} \= E\_\{k2\} \+ E\_\{p2\} \= mg\(h\-y\) \+ mgy \= mgh
Láthatjuk, hogy E\_\{mech1\} \= E\_\{mech2\} \= mgh, ami azt bizonyítja, hogy a mechanikai energia megmarad a szabadesés során (feltételezve, hogy a légellenállás elhanyagolható).
A földetérés pillanatában (y \= 0), a potenciális energia nulla (E\_\{p3\} \= 0), a kinetikus energia pedig:
E\_\{k3\} \= mg\(h\-0\) \= mgh
Így a mechanikai energia ekkor is E\_\{mech3\} \= mgh \+ 0 \= mgh. Az egész folyamat során a gravitációs potenciális energia folyamatosan kinetikus energiává alakul át, de a kettő összege (a mechanikai energia) állandó marad.
Egy Ideális Ingamozgása
Tekintsünk egy ideális ingát, amely egy \\mathbf\{L\} hosszúságú, súlytalan fonálon függő \\mathbf\{m\} tömegű testből áll, és súrlódás nélkül leng. Amikor az inga a legmagasabb pontján van (valamelyik szélső helyzetben), pillanatnyi sebessége nulla, így a kinetikus energiája is nulla. Ebben a pontban a gravitációs potenciális energiája maximális, a legalacsonyabb ponthoz (egyensúlyi helyzethez) viszonyít
Mechanikai Energia
A Mechanikai Energia Átfogó Értelmezése és Alkalmazásai
A mechanikai energia a fizika egyik alapvető fogalma, amely egy test vagy rendszer mozgásával és helyzetével kapcsolatos energiát írja le. Lényegében ez az az energia, amely lehetővé teszi a munkavégzést mechanikai úton. A mechanikai energia megértése kulcsfontosságú a klasszikus mechanika, a mérnöki tudományok és számos természeti jelenség magyarázatához. Ebben a részletes cikkben feltárjuk a mechanikai energia különböző aspektusait, beleértve annak definícióját, fajtáit, a megmaradás törvényét, az átalakulás folyamatait és a gyakorlati alkalmazásokat a mindennapi életben és a technológiában.
A Mechanikai Energia Definíciója és Alapelvei
A mechanikai energia egy rendszer azon képessége, hogy munkát végezzen. Ez magában foglalja a mozgással kapcsolatos energiát, amelyet kinetikus energiának nevezünk, és a helyzettel vagy konfigurációval kapcsolatos energiát, amelyet potenciális energiának hívunk. Egy mechanikai rendszer teljes energiája a kinetikus és potenciális energiájának összege, feltéve, hogy nincsenek disszipatív erők, mint például a súrlódás, amelyek hővé alakítják az energiát. A mechanikai energia szorosan kapcsolódik az erő és a mozgás fogalmaihoz, mivel az erők munkát végezhetnek, megváltoztatva egy test mozgását és ezáltal a mechanikai energiáját.
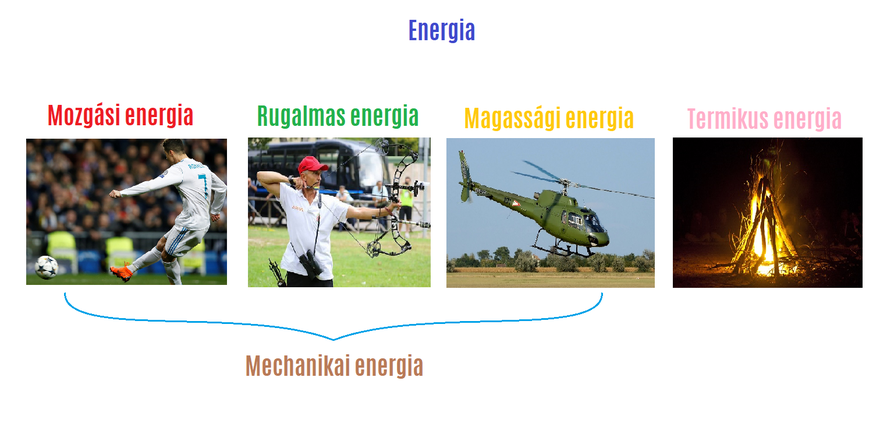
A Kinetikus Energia Részletes Bemutatása
A kinetikus energia egy mozgó test energiája. Minél nagyobb egy test tömege és sebessége, annál nagyobb a kinetikus energiája. Matematikailag a kinetikus energia (E\_k) a következőképpen fejezhető ki:
\\displaystyle E\_k \= \\frac\{1\}\{2\}mv^2

ahol m a test tömege (kilogrammban), és v a test sebessége (méter per másodpercben). Ebből az egyenletből látható, hogy a sebesség négyzetesen befolyásolja a kinetikus energiát, ami azt jelenti, hogy a sebesség kétszeresére növelése négyszeresére növeli a kinetikus energiát azonos tömeg mellett. A kinetikus energia skaláris mennyiség, ami azt jelenti, hogy csak nagysága van, iránya nincs.
Példák a Kinetikus Energiára a Mindennapi Életben
Számos példát találhatunk a kinetikus energiára a mindennapi életben. Egy guruló labda kinetikus energiával rendelkezik a mozgása miatt. Egy repülő repülőgép, egy futó ember vagy egy áramló víz mind rendelkezik kinetikus energiával. Minél gyorsabban mozognak, annál nagyobb a kinetikus energiájuk. A kinetikus energia hasznosítható is, például egy szélmalom a szél kinetikus energiáját alakítja át mechanikai munkává, amely aztán elektromos áramot termelhet.
A Potenciális Energia Részletes Bemutatása
A potenciális energia egy test vagy rendszer helyzetéből vagy konfigurációjából adódó tárolt energia. Többféle formája létezik, attól függően, hogy milyen erőhatás hozza létre. A mechanikában leggyakrabban a gravitációs potenciális energiával és a rugalmas potenciális energiával találkozunk.
Gravitációs Potenciális Energia
A gravitációs potenciális energia egy testnek a gravitációs mezőben elfoglalt helyzetéből adódik. A Föld felszínén egy h magasságban lévő m tömegű test gravitációs potenciális energiája (E\_p) a következőképpen számítható ki:

\\displaystyle E\_p \= mgh
ahol g a gravitációs gyorsulás (a Földön körülbelül 9\.81 \\, m/s^2). Ebből az egyenletből látható, hogy minél magasabban van egy test, annál nagyobb a gravitációs potenciális energiája egy adott referencia szinthez képest (általában a Föld felszíne). A gravitációs potenciális energia is skaláris mennyiség.
Példák a Gravitációs Potenciális Energiára
Egy hegy tetején álló kő gravitációs potenciális energiával rendelkezik a magassága miatt. Ha a kő leesik, ez a potenciális energia kinetikus energiává alakul át. Egy víztározóban felgyülemlett víz szintén gravitációs potenciális energiával rendelkezik, amelyet a vízerőművek elektromos áram termelésére használnak fel, amikor a vizet leengedik turbinákon keresztül.
Rugalmas Potenciális Energia
A rugalmas potenciális energia egy rugalmasan deformálódott testben tárolt energia, például egy megnyújtott vagy összenyomott rugóban. A rugalmas potenciális energia (E\_\{rug\}) egy ideális rugó esetében a következőképpen fejezhető ki (Hooke törvényéből származtatva):
\\displaystyle E\_\{rug\} \= \\frac\{1\}\{2\}kx^2
ahol k a rugóállandó (amely a rugó merevségét jellemzi), és x a rugó egyensúlyi helyzetétől való elmozdulása (megnyúlása vagy összenyomódása). A rugalmas potenciális energia is skaláris mennyiség.
Példák a Rugalmas Potenciális Energiára
Egy összenyomott rugó rugalmas potenciális energiával rendelkezik, amely felszabadulhat, ha a rugó kinyílik, például egy játékpisztolyban, amely egy golyót lő ki. Egy megfeszített íj húrjában is rugalmas potenciális energia tárolódik, amely a nyíl kilövéséhez szükséges kinetikus energiává alakul át.
A Mechanikai Energia Megmaradásának Törvénye
A mechanikai energia megmaradásának törvénye az egyik legalapvetőbb elv a fizikában. Kimondja, hogy egy izolált rendszerben, ahol csak konzervatív erők (mint a gravitáció és a rugalmas erő) hatnak, a rendszer teljes mechanikai energiája (a kinetikus és a potenciális energia összege) állandó marad az időben. Matematikailag ezt így fejezhetjük ki:
\\displaystyle E\_\{mechanikai\} \= E\_k \+ E\_p \= állandó
Ez azt jelenti, hogy az energia nem vész el és nem keletkezik, csak átalakulhat egyik formából a másikba. Például, amikor egy test leesik, a gravitációs potenciális energiája kinetikus energiává alakul át, de a kettő összege állandó (ha elhanyagoljuk a légellenállást).
Konzervatív és Nemkonzervatív Erők
A mechanikai energia megmaradásának törvénye csak akkor érvényes, ha a rendszerben ható erők konzervatívak. Egy erő akkor konzervatív, ha az általa végzett munka független az úttól, csak a kezdő- és végponttól függ. A gravitációs erő és a rugalmas erő példák konzervatív erőkre. Ezzel szemben a nemkonzervatív erők, mint a súrlódás vagy a légellenállás, olyan munkát végeznek, amely függ az úttól, és az általuk végzett munka nem téríthető vissza teljes mértékben más energiaformává (általában hővé alakul). Ha nemkonzervatív erők is jelen vannak, a rendszer teljes mechanikai energiája nem marad állandó, hanem csökkenhet.
Példa a Mechanikai Energia Megmaradására: A Lengőinga
Egy klasszikus példa a mechanikai energia megmaradására a lengőinga. Amikor az inga a legmagasabb pontján van, a sebessége nulla, így a kinetikus energiája is nulla, de a gravitációs potenciális energiája maximális. Ahogy az inga lefelé lendül, a potenciális energia kinetikus energiává alakul át, és a legalacsonyabb ponton a kinetikus energia maximális, míg a potenciális energia minimális (a választott referencia szinttől függően). Ha nem lenne légellenállás és súrlódás a felfüggesztési pontban, az inga örökké lengene, folyamatosan átalakítva a potenciális és kinetikus energiát egymásba, miközben a teljes mechanikai energia állandó maradna.
A Mechanikai Energia Átalakulásai
A mechanikai energia gyakran alakul át más energiaformákká és fordítva. Ahogy fentebb említettük, a potenciális energia kinetikus energiává alakulhat (például egy leeső tárgy esetében), és a kinetikus energia potenciális energiává (például egy felfelé dobott labda esetében, amely lelassul a legmagasabb pontján). Emellett a mechanikai energia átalakulhat hővé (például súrlódás következtében), hanggá (például egy ütközéskor) vagy akár elektromos energiává (például egy generátorban).
Példák a Mechanikai Energia Átalakulására
- Egy autó fékezésekor a mozgási energia (kinetikus energia) a fékekben hővé alakul át a súrlódás miatt.
- Egy vízerőműben a víz gravitációs potenciális energiája először a víz mozgási energiájává alakul át, majd a turbinák forgatásával mechanikai munkává, végül pedig egy generátor segítségével elektromos energiává.
- Amikor egy kalapáccsal egy szögbe ütünk, a kalapács mozgási energiája részben a szög mozgási energiájává és a fa deformálásához szükséges munkává alakul, emellett hő és hang is keletkezik.
- Egy trambulinon ugráló ember folyamatosan alakítja át a gravitációs potenciális energiát rugalmas potenciális energiává (a trambulin rugóiban vagy anyagában) és kinetikus energiává.


A Munka és a Mechanikai Energia Kapcsolata
A munka szorosan kapcsolódik a mechanikai energiához. A munka egy erő által végzett energiaátadás, amikor az erő elmozdít egy testet. Ha egy erő munkát végez egy testen, az megváltoztathatja a test mechanikai energiáját. A munka-energia tétel kimondja, hogy egy testre ható összes erő által végzett nettó munka egyenlő a test kinetikus energiájának megváltozásával:
\\displaystyle W\_\{nettó\} \= \\Delta E\_k \= E\_\{k,végső\} \- E\_\{k,kezdeti\}
Ha csak konzervatív erők végeznek munkát, akkor a teljes mechanikai energia megmarad, ami azt jelenti, hogy a kinetikus energia megváltozása egyenlő a potenciális energia negatív megváltozásával:
\\displaystyle \\Delta E\_k \= \-\\Delta E\_p
vagyis
\\displaystyle \\Delta \(E\_k \+ E\_p\) \= \\Delta E\_\{mechanikai\} \= 0
A Munka Számítása
A munka (W) egy állandó \\mathbf\{F\} erő által végzett munka, amely egy testet \\mathbf\{d\} vektorral elmozdít, a következőképpen számítható ki a skaláris szorzat segítségével:
\\displaystyle W \= \\mathbf\{F\} \\cdot \\mathbf\{d\} \= \|\\mathbf\{F\}\| \|\\mathbf\{d\}\| \\cos \\theta
ahol \|\\mathbf\{F\}\| az erő nagysága, \|\\mathbf\{d\}\| az elmozdulás nagysága, és \\theta az erő és az elmozdulás közötti szög. A munka mértékegysége a joule (J), amely megegyezik egy newton méterrel (N·m).
A Mechanikai Energia Gyakorlati Alkalmazásai
A mechanikai energia elvének megértése és alkalmazása számos technológiai és mérnöki területen elengedhetetlen. Néhány példa:
Energiatermelés
Sok energiatermelési módszer a mechanikai energia átalakításán alapul. A vízerőművek a víz gravitációs potenciális energiáját alakítják át először kinetikus energiává, majd mechanikai munkává a turbinák forgatásával, végül elektromos energiává a generátorokban. A szélenergia a szél kinetikus energiáját használja fel szélturbinák forgatására, ami mechanikai munkát végez, amelyet aztán elektromos árammá alakítanak. A hőerőművekben a hőenergia gőzt termel, amely turbinákat forgatva mechanikai energiát hoz létre, amit aztán elektromos árammá alakítanak.
Közlekedés
A közlekedési eszközök nagymértékben a mechanikai energiára támaszkodnak. A gépjárművek belső égésű motorjai vagy elektromos motorjai mechanikai munkát végeznek a kerekek forgatásához, ami mozgást eredményez. A repülőgépek hajtóművei tolóerőt generálnak, ami a repülőgép kinetikus energiájának növekedéséhez vezet. A vonatok elektromos vagy dízelmotorjai szintén mechanikai energiát használnak a mozgáshoz.
Gyártás és Ipari Folyamatok
A gyártásban és az ipari folyamatokban a mechanikai energia kulcsfontosságú a gépek működtetéséhez. Szerszámgépek, robotok és futószalagok mind mechanikai energiát használnak a feladatok elvégzéséhez. A hidraulikus és pneumatikus rendszerek folyadékok vagy gázok nyomását használják fel mechanikai munka végzésére.
Sport és Szórakozás
A mechanikai energia számos sportban és szórakozási formában is szerepet játszik. Egy labda eldobása vagy egy íjból kilőtt nyíl a testnek adott kinetikus energián alapul. A hullámvasutak a gravitációs potenciális energia és a kinetikus energia folyamatos átalakulásán alapulnak, izgalmas élményt nyújtva.
Összefoglalás
A mechanikai energia a mozgással és a helyzettel kapcsolatos energia, amely két fő formában létezik: kinetikus energia (a mozgás energiája) és potenciális energia (a helyzet vagy konfiguráció energiája). A mechanikai energia megmaradásának törvénye szerint egy izolált rendszer teljes mechanikai energiája állandó marad, ha csak konzervatív erők hatnak. A mechanikai energia folyamatosan átalakulhat más energiaformákká és fordítva, és szorosan kapcsolódik a munkához. A mechanikai energia elvének megértése elengedhetetlen a fizika, a mérnöki tudományok és számos gyakorlati alkalmazás szempontjából, az energiatermeléstől a közlekedésen át a gyártásig és a szórakozásig.