Helyzeti Energia Szamitasa

A Helyzeti Energia Számítása: Részletes Útmutató

Ebben az átfogó útmutatóban részletesen feltárjuk a helyzeti energia fogalmát, a számításának módjait, a különböző típusait és azok gyakorlati alkalmazásait. Célunk, hogy egy olyan mélyreható ismeretanyagot nyújtsunk, amely mindenki számára érthetővé teszi a potenciális energia világát, legyen szó diákokról, tanárokról vagy a fizika iránt érdeklődő laikusokról.

Mi a Helyzeti Energia (Potenciális Energia)?

A helyzeti energia, más néven potenciális energia, egy olyan energiaforma, amely egy objektum helyzetéből vagy konfigurációjából adódik egy erőmezőn belül. Ez azt jelenti, hogy az objektum képes munkát végezni a helyzetének vagy konfigurációjának megváltozásával. A potenciális energia nem önmagában létezik, hanem mindig egy erőmezőhöz kapcsolódik, mint például a gravitációs mező, az elektromos mező vagy a rugalmas erő tere.

A Gravitációs Potenciális Energia

A leggyakrabban emlegetett formája a helyzeti energiának a gravitációs potenciális energia. Ez az energia egy objektum tömegéből és a gravitációs mezőben elfoglalt magasságából származik. Minél magasabban van egy objektum a referencia szinthez képest (általában a Föld felszíne), annál nagyobb a gravitációs potenciális energiája. Amikor ez az objektum leesik, a potenciális energia mozgási energiává alakul át.

A Gravitációs Potenciális Energia Képlete

A gravitációs potenciális energia (E\_p) számításának képlete a következő:

\\mathbf\{E\_p \= m \\cdot g \\cdot h\}

ahol:

• \\mathbf\{m\} az objektum tömege (kilogrammban, kg)
• \\mathbf\{g\} a gravitációs gyorsulás a Föld felszínén (körülbelül 9\.81 \\, m/s^2)
• \\mathbf\{h\} az objektum magassága a referencia szinthez képest (méterben, m)

Példa a Gravitációs Potenciális Energia Számítására

Képzeljünk el egy 2 \\, kg tömegű könyvet, amely egy 1\.5 \\, m magas polcon van. A könyv gravitációs potenciális energiája a Föld felszínéhez képest:

\\mathbf\{E\_p \= 2 \\, kg \\cdot 9\.81 \\, m/s^2 \\cdot 1\.5 \\, m \= 29\.43 \\, J\}

Tehát a könyv 29\.43 \\, Joule gravitációs potenciális energiával rendelkezik.

A Referencia Szint Fontossága

Fontos megjegyezni, hogy a gravitációs potenciális energia relatív fogalom, mivel függ a választott referencia szinttől. Általában a Föld felszínét tekintjük referencia szintnek, ahol a magasság h\=0, és így a potenciális energia is nulla. Azonban bizonyos problémák esetén más referencia szintek is praktikusak lehetnek.

A Rugalmas Potenciális Energia

Egy másik fontos típusa a helyzeti energiának a rugalmas potenciális energia. Ez az energia akkor tárolódik egy rugalmas testben (például egy rugóban), amikor azt megnyújtják vagy összenyomják az eredeti egyensúlyi helyzetéhez képest. A rugalmas erő, amely visszaállítja a rugót az egyensúlyi helyzetébe, végzi a munkát.

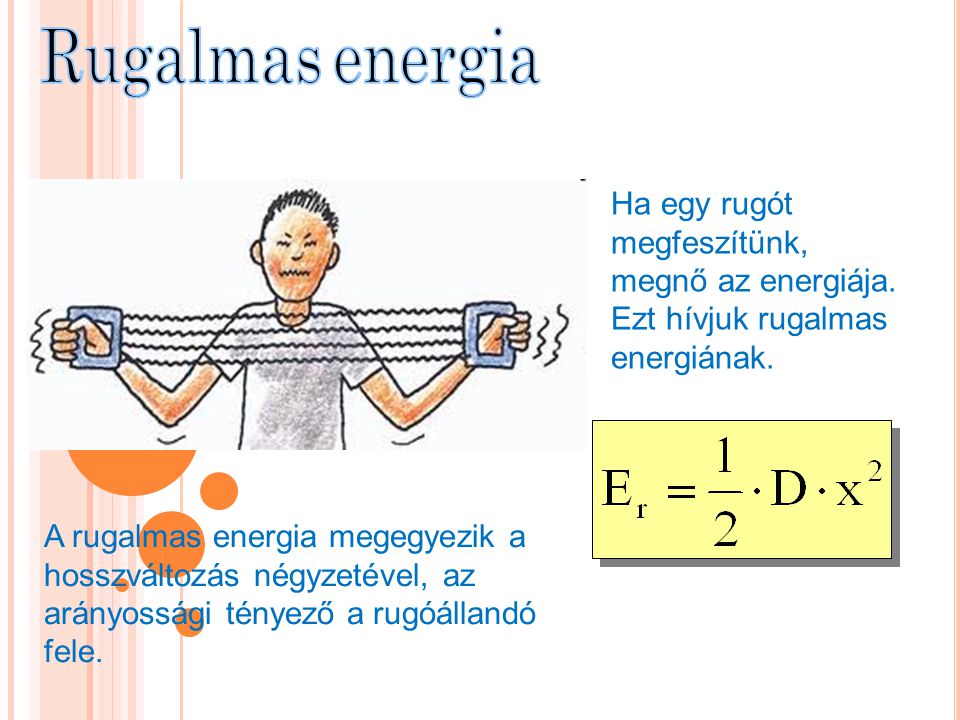
A Rugalmas Potenciális Energia Képlete

A rugalmas potenciális energia (E\_\{pr\}) számításának képlete a következő:

\\mathbf\{E\_\{pr\} \= \\frac\{1\}\{2\} \\cdot k \\cdot x^2\}

ahol:

• \\mathbf\{k\} a rugó rugóállandója (Newton/méterben, N/m), amely a rugó merevségét jellemzi.
• \\mathbf\{x\} a rugó megnyúlása vagy összenyomódása az egyensúlyi helyzetéhez képest (méterben, m).

Példa a Rugalmas Potenciális Energia Számítására

Tekintsünk egy rugót, amelynek rugóállandója 100 \\, N/m. Ha ezt a rugót 0\.1 \\, m-rel megnyújtjuk, a benne tárolt rugalmas potenciális energia:

\\mathbf\{E\_\{pr\} \= \\frac\{1\}\{2\} \\cdot 100 \\, N/m \\cdot \(0\.1 \\, m\)^2 \= 0\.5 \\, J\}

Tehát a megnyújtott rugó 0\.5 \\, Joule rugalmas potenciális energiával rendelkezik.

Egyéb Potenciális Energia Típusok

A gravitációs és a rugalmas potenciális energia mellett léteznek más formái is a helyzeti energiának:

• Elektromos potenciális energia: Két elektromos töltés közötti kölcsönhatásból származik.
• Mágneses potenciális energia: Mágneses mezőben lévő mágneses dipólus energiája.
• Kémiai potenciális energia: Az atomok és molekulák közötti kémiai kötésekben tárolt energia.
• Nukleáris potenciális energia: Az atommagban lévő nukleonok közötti kölcsönhatásból származó energia.

Bár ezek nem közvetlenül a “helyzetből” adódnak a szó szoros értelmében, mégis potenciális energiának nevezzük őket, mert egy adott konfigurációban tárolódnak, és felszabadulhatnak, munkát végezve.

A Helyzeti Energia Számításának Általános Elvei

Általánosságban elmondható, hogy a potenciális energia számítása egy adott erőmezőben a következőképpen történik:

1. Meg kell határozni az erőmezőt (pl. gravitációs, rugalmas).
2. Ki kell választani egy referencia pontot vagy konfigurációt, ahol a potenciális energia nulla.
3. A potenciális energia a munkával egyenlő, amelyet az erőmező végez ahhoz, hogy az objektumot a referencia pontból az aktuális helyzetébe vagy konfigurációjába vigye (vagy fordítva, az aktuális helyzetből a referencia pontba).

A Munkavégzés és a Potenciális Energia Kapcsolata

A potenciális energia szorosan kapcsolódik a munkavégzés fogalmához. Ha egy konzervatív erő (mint a gravitációs erő vagy a rugalmas erő) munkát végez egy objektumon, akkor a rendszer potenciális energiája megváltozik. A munkavégzés nagysága egyenlő a potenciális energia változásának negatívjával:

\\mathbf\{W \= \-\\Delta E\_p\}

Ez azt jelenti, hogy ha az erő munkát végez az objektumon (pl. egy leeső tárgy esetén a gravitáció), akkor a potenciális energia csökken. Ha pedig külső erő munkát végez az objektumon a konzervatív erő ellenében (pl. egy tárgy felemelése), akkor a potenciális energia nő.

A Helyzeti Energia Gyakorlati Alkalmazásai

A helyzeti energia fogalma és számítása számos területen kulcsfontosságú:

Energiatermelés

A vízerőművek a gravitációs potenciális energiát használják fel elektromos áram előállítására. A magasabban elhelyezkedő víztározókban tárolt víz potenciális energiával rendelkezik, amely mozgási energiává alakul át, amikor a vizet leengedik a turbinákon keresztül, megforgatva azokat és generátorokat hajtva.

Mechanikai Rendszerek

A rugók széles körben alkalmazásra kerülnek mechanikai rendszerekben, például felfüggesztésekben, órákban és különféle eszközökben. A bennük tárolt rugalmas potenciális energia lehetővé teszi a mozgást és az erő kifejtését.

Sport és Szórakozás

A hullámvasutak működése nagymértékben a gravitációs potenciális energián alapul. A kocsikat egy magas pontra húzzák fel, ahol nagy a potenciális energiájuk, majd ez az energia mozgási energiává alakul át a lejtőkön lefelé haladva.

Tárolt Energia

A akkumulátorokban és más energiatároló eszközökben kémiai potenciális energia tárolódik, amely elektromos energiává alakítható át szükség esetén.

Összefoglalás

A helyzeti energia vagy potenciális energia egy alapvető fogalom a fizikában, amely egy objektum helyzetéből vagy konfigurációjából adódik egy erőmezőn belül. Két fő típusát vizsgáltuk részletesen: a gravitációs potenciális energiát (E\_p \= m \\cdot g \\cdot h) és a rugalmas potenciális energiát (E\_\{pr\} \= \\frac\{1\}\{2\} \\cdot k \\cdot x^2). Megbeszéltük a számításuk módjait, a referencia szint fontosságát és a gyakorlati alkalmazásaikat az energiatermeléstől a mechanikai rendszereken át a sportig.

Reméljük, hogy ez a részletes útmutató segített megérteni a helyzeti energia lényegét és számításának módjait. Ha további kérdései vannak, ne habozzon feltenni!

A Gravitációs Potenciális Energia Mélyebben

A gravitációs potenciális energia nem csupán egy egyszerű képletet takar. Valójában a gravitációs mezőben végzett munka eredménye, amikor egy tömeget egy adott pontból egy másik pontba mozgatunk. A gravitációs erő egy konzervatív erő, ami azt jelenti, hogy a munkavégzése nem függ az úttól, csupán a kezdő- és végpont helyzetétől.

A Gravitációs Erő és a Munkavégzés

A Föld felszínén egy m tömegű objektumra ható gravitációs erő lefelé irányul, és nagysága F\_g \= m \\cdot g. Ha ezt az objektumot függőlegesen felfelé mozgatjuk egy h magasságra, akkor a külső erőnek (amely legyőzi a gravitációt) W \= F \\cdot d \= \(m \\cdot g\) \\cdot h munkát kell végeznie. Ez a bevitt munka tárolódik az objektumban gravitációs potenciális energiaként.

A Potenciális Energia Függése a Magasságtól

Ahogy a képlet is mutatja (E\_p \= m \\cdot g \\cdot h), a gravitációs potenciális energia egyenesen arányos az objektum tömegével és a referencia szint feletti magasságával. Egy kétszer akkora tömegű objektum azonos magasságban kétszer akkora potenciális energiával rendelkezik. Hasonlóképpen, egy objektum kétszer akkora magasságban kétszer akkora potenciális energiával rendelkezik (ugyanazon tömeg mellett).

Általános Gravitációs Potenciális Energia

A Föld felszínétől távolabb, vagy két tetszőleges tömeg közötti gravitációs potenciális energia leírásához az általános gravitációs törvényt kell használnunk. Két m\_1 és m\_2 tömeg közötti gravitációs potenciális energia, amelyek r távolságra vannak egymástól:

\\mathbf\{U \= \-G \\frac\{m\_1 m\_2\}\{r\}\}

ahol G az univerzális gravitációs állandó (6\.674 \\times 10^\{\-11\} \\, N \\cdot m^2/kg^2). Ebben az esetben a referencia pont a végtelen távolság (r \\rightarrow \\infty), ahol a potenciális energia nulla.

A Föld felszínénél alkalmazott E\_p \= m \\cdot g \\cdot h képlet valójában ennek az általánosabb képletnek egy közelítése, amikor a magasság h sokkal kisebb, mint a Föld sugara.

A Rugalmas Potenciális Energia Részletesebben

A rugalmas potenciális energia a rugalmas erő munkájának eredménye. A Hooke-törvény szerint egy ideális rugó által kifejtett erő (F\_r) egyenesen arányos a rugó egyensúlyi helyzetétől való elmozdulásával (x):

\\mathbf\{F\_r \= \-k \\cdot x\}

A negatív előjel azt jelzi, hogy a rugóerő mindig az elmozdulással ellentétes irányú, azaz visszaállító erő.

A Munkavégzés a Rugó Megnyújtásakor vagy Összenyomásakor

Ahhoz, hogy egy rugót megnyújtsunk vagy összenyomjunk egy x távolsággal, külső erőre van szükség, amely legyőzi a rugóerőt. Az ehhez szükséges munka a rugalmas potenciális energiában tárolódik. A munkát az erő integráljával számíthatjuk ki az elmozdulás mentén:

\\mathbf\{W \= \\int\_\{0\}^\{x\} F\_\{ext\} \\, dx \= \\int\_\{0\}^\{x\} kx \\, dx \= \\frac\{1\}\{2\} k x^2\}

Mivel a munkavégzés egyenlő a potenciális energia megváltozásával (a referencia pont a x\=0 egyensúlyi helyzet), kapjuk a rugalmas potenciális energia képletét: E\_\{pr\} \= \\frac\{1\}\{2\} k x^2.

A Rugóállandó Jelentősége

A rugóállandó (k) a rugó merevségének mértéke. Egy nagy k értékű rugó merevebb, nagyobb erőre van szükség az azonos mértékű megnyújtásához vagy öss