Energiamegmaradas Torvenye Definicio
Az Energiamegmaradás Törvénye: A Világegyetem Alapvető Elve
Az energiamegmaradás törvénye a fizika egyik legfontosabb és legalapvetőbb elve, amely kimondja, hogy egy izolált rendszer teljes energiája időben állandó marad. Ez azt jelenti, hogy az energia nem keletkezhet a semmiből és nem veszhet el, csupán egyik formájából átalakulhat egy másikba. Ez a tétel áthatja a természettudományok szinte minden területét, a klasszikus mechanikától a termodinamikán át az elektromágnesességig és a részecskefizikáig. Az energia megmaradása nem csupán egy elméleti konstrukció, hanem számtalan kísérleti megfigyelés és gyakorlati alkalmazás támasztja alá.
Az Energiamegmaradás Törvényének Definíciója és Mélyebb Értelmezése

A legegyszerűbb megfogalmazás szerint az energiamegmaradás törvénye azt állítja, hogy egy zárt rendszerben az energia mennyisége nem változik. Fontos kiemelni a “zárt rendszer” fogalmát. Egy zárt rendszer olyan rendszer, amely nem cserél energiát a környezetével. A valóságban tökéletesen zárt rendszerek ritkán léteznek, de sok esetben a vizsgált rendszer olyan mértékben van elszigetelve a környezetétől, hogy az energiaáramlás elhanyagolható. Ha egy rendszer nem zárt, akkor az energiája megváltozhat a környezetével való energiaátadás következtében (pl. hő formájában végzett munka).
Az energia egy absztrakt fogalom, amely a munka végzésének képességét vagy a hőátadás lehetőségét írja le. Különböző formákban jelenhet meg, mint például a kinetikus energia (mozgási energia), a potenciális energia (helyzeti energia), a hőenergia (a részecskék mozgásából származó energia), az elektromágneses energia (elektromos és mágneses mezőkhöz kapcsolódó energia), a kémiai energia (a kémiai kötésekben tárolt energia) és a nukleáris energia (az atommagban tárolt energia). Az energiamegmaradás törvénye azt mondja ki, hogy egy zárt rendszerben ezen energiafajták összessége állandó, bár az egyik forma átalakulhat egy másikba.
Az Energiamegmaradás Történeti Áttekintése

Az energiamegmaradás gondolata nem egyetlen pillanatban fogalmazódott meg, hanem tudósok és filozófusok évszázados munkájának eredménye. Már a korai gondolkodók is felismerték, hogy valamilyen állandóság létezik a természeti jelenségek mögött. A 17. században például Gottfried Wilhelm Leibniz bevezette a “vis viva” (élő erő) fogalmát, amely a mai kinetikus energia fogalmának elődje volt ($mv^2$). Leibniz úgy vélte, hogy a természetben a “vis viva” megmarad.
A 19. század elején olyan tudósok, mint Julius Robert Mayer, James Prescott Joule és Hermann von Helmholtz, egymástól függetlenül jutottak arra a felismerésre, hogy a hő és a mechanikai munka ekvivalens formái az energiának, és hogy az energia összességében megmarad. Joule kísérletei, amelyekben mechanikai munkával hőt fejlesztett, kulcsfontosságúak voltak az energiamegmaradás elvének kísérleti alátámasztásában. Helmholtz pedig 1847-ben megjelent “Über die Erhaltung der Kraft” (Az erő megmaradásáról) című munkájában fogalmazta meg az energiamegmaradás általános elvét.
A Termodinamika Első Főtétele és az Energiamegmaradás
A termodinamika első főtétele az energiamegmaradás törvényének egyik legfontosabb megfogalmazása a termodinamikai rendszerekre. Kimondja, hogy egy zárt rendszer belső energiájának ($U$) megváltozása egyenlő a rendszerrel közölt hő ($Q$) és a rendszeren végzett munka ($W$) összegével: $$\Delta U = Q + W$$. Ez az egyenlet azt fejezi ki, hogy az energia nem vész el és nem keletkezik, csupán a rendszer és a környezete között cserélődhet hő vagy munka formájában, ami megváltoztatja a rendszer belső energiáját.
Az Energiamegmaradás Matematikai Megfogalmazásai
Az energiamegmaradás törvényét különböző matematikai formákban is ki lehet fejezni, attól függően, hogy milyen rendszert vizsgálunk. A klasszikus mechanikában egy konzervatív erőterekben mozgó részecskerendszer teljes energiája ($E$), amely a kinetikus energia ($K$) és a potenciális energia ($U_{pot}$) összege, időben állandó: $$E = K + U_{pot} = \text{állandó}$$. Ha nem konzervatív erők (pl. súrlódás) is jelen vannak, akkor a mechanikai energia nem marad meg, hanem más energiaformákká (pl. hővé) alakul át, de a rendszer és a környezet teljes energiája továbbra is megmarad.
A kvantummechanikában az energiamegmaradás szintén alapvető fontosságú. A Schrödinger-egyenlet időfüggő formája írja le egy kvantumrendszer állapotának időbeli fejlődését, és ha a Hamilton-operátor (amely a rendszer energiáját reprezentálja) nem függ explicit módon az időtől, akkor a rendszer energiája megmarad.
Az Energia Különböző Formái és Azok Átalakulásai
Ahogy korábban említettük, az energia számos formában létezhet, és az energiamegmaradás törvénye lehetővé teszi, hogy megértsük, hogyan alakul át egyik forma a másikba. Nézzünk meg néhány példát:
- Mechanikai energia: Kinetikus energia (mozgás) és potenciális energia (helyzet vagy konfiguráció). Például egy leejtett labda potenciális energiája fokozatosan kinetikus energiává alakul át, miközben esik. A becsapódáskor ez a kinetikus energia részben hővé és hanggá alakul.
- Hőenergia: Az atomok és molekulák véletlenszerű mozgásából származik. Amikor egy testet felmelegítünk, a részecskéinek mozgási energiája nő. A hőenergia átadható egyik testről a másikra hővezetés, hőáramlás vagy hősugárzás útján.
- Elektromágneses energia: Az elektromos és mágneses mezőkhöz kapcsolódik. Ide tartozik a fény, a rádióhullámok, a röntgensugarak stb. Egy elektromos motor az elektromos energiát mechanikai energiává alakítja, míg egy generátor a mechanikai energiát elektromos energiává.
- Kémiai energia: A molekulákban lévő kémiai kötésekben tárolódik. Kémiai reakciók során ez az energia felszabadulhat (exoterm reakciók) vagy elnyelődhet (endoterm reakciók). Például az égés során a kémiai energia hővé és fényé alakul.
- Nukleáris energia: Az atommagban tárolt energia. Atommagreakciók (pl. maghasadás, magfúzió) során hatalmas mennyiségű energia szabadulhat fel.


Az energiamegmaradás törvénye azt biztosítja, hogy bár az energia formája megváltozhat, a teljes mennyisége egy zárt rendszerben mindig ugyanaz marad.
Gyakorlati Alkalmazások: Hogyan Használjuk Ki az Energiamegmaradás Elvét?
Az energiamegmaradás törvényének megértése és alkalmazása elengedhetetlen a tudomány és a technológia számos területén:
- Energiatermelés: A különböző erőművek (hőerőművek, vízerőművek, szélerőművek, atomerőművek) mind az energia egyik formájának egy másikba történő átalakításán alapulnak. Például egy vízerőmű a víz potenciális energiáját alakítja át először kinetikus energiává, majd elektromos energiává.
- Közlekedés: A járművek (autók, repülők, vonatok) működése szintén az energiaátalakításon alapul. Egy belső égésű motor a kémiai energiát alakítja át mechanikai munkává.
- Építészet és épületgépészet: Az energiahatékony épületek tervezése és a fűtési, szellőztetési rendszerek optimalizálása az energiamegmaradás elvén alapul. A hőszigetelés például csökkenti a hőveszteséget, így kevesebb energiára van szükség a fűtéshez.
- Kémia: A kémiai reakciók energiaváltozásainak megértése és előrejelzése a termodinamika, és ezen belül az energiamegmaradás alapvető fontosságú.
- Biológia: Az élőlények anyagcseréje és működése energiaátalakítási folyamatok sorozata. A táplálékban tárolt kémiai energia alakul át a sejtek által hasznosítható energiává.

Az Energiamegmaradás és a Perpetuum Mobile
Az energiamegmaradás törvénye közvetlenül cáfolja a perpetuum mobile létezését. A perpetuum mobile egy olyan hipotetikus gép, amely külső energiaforrás nélkül képes folyamatosan munkát végezni (elsőfajú perpetuum mobile) vagy a környezetéből hőt elvonva azt teljes egészében munkává alakítani (másodfajú perpetuum mobile). Az energiamegmaradás kimondja, hogy energia nem teremthető a semmiből, ezért egy elsőfajú perpetuum mobile nem létezhet. A termodinamika második főtétele pedig kizárja a másodfajú perpetuum mobile lehetőségét is.
Az Energiamegmaradás Kiterjesztése: A Tömeg-Energia Ekvivalencia
Albert Einstein speciális relativitáselmélete forradalmasította az energiamegmaradás fogalmát a híres $E=mc^2$ egyenletével. Ez az egyenlet kifejezi a tömeg és az energia ekvivalenciáját, ami azt jelenti, hogy a tömeg az energia egyik formája, és az energia tömeggé alakulhat, és fordítva. Ez különösen fontos a nukleáris reakciókban, ahol mérhető tömegveszteség tapasztalható, amely az energiamegmaradás értelmében energiává alakul.
A Megújuló Energiaforrások és az Energiamegmaradás
A megújuló energiaforrások (napenergia, szélenergia, vízenergia, geotermikus energia, biomassza) mind olyan természeti folyamatokból származnak, amelyek végső soron a Nap energiájára vagy a Föld belső hőjére vezethetők vissza. Ezek az energiaforrások az energiamegmaradás elvét követve alakítják át a rendelkezésre álló energiát hasznos formákká anélkül, hogy kimerítenék az energiaforrást a szó hagyományos értelmében.
Összefoglalás: Az Energiamegmaradás Törvényének Fontossága

Az energiamegmaradás törvénye a fizika egyik sarokköve, amely nélkül a természeti jelenségek megértése és a technológiai fejlesztések elképzelhetetlenek lennének. Ez az alapelv nem csupán leírja a világ működését, hanem korlátokat is szab a lehetséges folyamatoknak (például a perpetuum mobile lehetetlensége). Az energia megmaradása biztosítja a kozmosz bizonyos szintű állandóságát és lehetővé teszi számunkra, hogy megértsük az energia különböző formái közötti kapcsolatokat és átalakulásokat.
Reméljük, hogy ez az átfogó cikk segített megérteni az energiamegmaradás törvényének lényegét és jelentőségét. Ha további kérdései vannak, ne habozzon feltenni őket!
Mechanikai Energiafajtak
A Mechanikai Energia Fajtái: Átfogó Kézikönyv
A mechanikai energia a fizika egyik alapvető fogalma, amely egy test vagy rendszer mozgásával és helyzetével kapcsolatos energiát írja le. Ez az energiaforma kulcsfontosságú a makroszkopikus világ jelenségeinek megértéséhez, a mindennapi tapasztalatainktól kezdve a komplex mérnöki alkalmazásokig. Ebben a részletes útmutatóban feltárjuk a mechanikai energia különböző fajtáit, azok jellemzőit, megjelenési formáit és a velük kapcsolatos alapvető fizikai törvényeket.
A Mechanikai Energia Alapjai
A mechanikai energia fogalma szorosan kapcsolódik a munkavégzés képességéhez. Ha egy erő egy testet elmozdít, munkát végez rajta, és ez a munka megváltoztathatja a test mechanikai energiáját. A mechanikai energia két fő összetevőre bontható: a kinetikus energiára és a potenciális energiára. Ezek az energiafajták együttesen határozzák meg egy rendszer teljes mechanikai energiáját.
Kinetikus Energia: A Mozgás Energiája
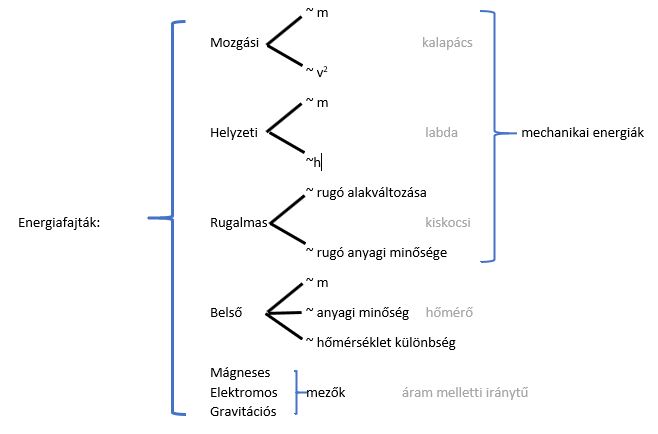
A kinetikus energia egy test mozgásából származó energia. Minden olyan objektum, amely mozog, rendelkezik kinetikus energiával. Ennek az energiának a nagysága függ a test tömegétől és sebességétől. Minél nagyobb a test tömege vagy sebessége, annál nagyobb a kinetikus energiája. A kinetikus energia képlete a következő:
\\mathbf\{E\_k \= \\frac\{1\}\{2\}mv^2\}
ahol \(E_k\) a kinetikus energia, \(m\) a test tömege, és \(v\) a test sebessége.
Példák a Kinetikus Energiára
- Egy száguldó autó: Minél gyorsabban halad az autó, annál nagyobb a kinetikus energiája. Egy nehezebb autó azonos sebességnél szintén nagyobb kinetikus energiával rendelkezik.
- Egy repülő labda: A labda mozgása során kinetikus energiával rendelkezik. A dobás erőssége és a labda tömege befolyásolja ezt az energiát.
- Egy forgó kerék: A forgó kerék részei folyamatos mozgásban vannak, így a kerék rendelkezik kinetikus energiával.
A kinetikus energia nem csak a lineáris mozgáshoz kapcsolódik, hanem a forgó mozgáshoz is. A forgó testek forgási kinetikus energiával rendelkeznek, amely a test tehetetlenségi nyomatékától és szögsebességétől függ.
\\mathbf\{E\_\{rot\} \= \\frac\{1\}\{2\}I\\omega^2\}
ahol \(E_{rot}\) a forgási kinetikus energia, \(I\) a tehetetlenségi nyomaték, és \(\omega\) a szögsebesség.
Potenciális Energia: A Helyzetből Adódó Energia
A potenciális energia egy test helyzetéből vagy konfigurációjából származó tárolt energia. Ez az energia akkor szabadulhat fel, ha a test megváltoztatja a helyzetét vagy konfigurációját. A mechanikában két fő típusa van a potenciális energiának: a gravitációs potenciális energia és a rugalmas potenciális energia.

Gravitációs Potenciális Energia
A gravitációs potenciális energia egy testnek a gravitációs mezőben elfoglalt helyzetéből adódik. A Föld felszínén egy \(h\) magasságban lévő \(m\) tömegű test gravitációs potenciális energiája a következőképpen számítható ki:
\\mathbf\{E\_p \= mgh\}
ahol \(E_p\) a gravitációs potenciális energia, \(m\) a test tömege, \(g\) a gravitációs gyorsulás (a Földön körülbelül \(9.81 \, m/s^2\)), és \(h\) a test magassága egy referencia szinthez képest.
Példák a Gravitációs Potenciális Energiára
- Egy hegy tetején lévő kő: A kőnek magasságából adódóan gravitációs potenciális energiája van. Ha a kő leesik, ez az energia kinetikus energiává alakul át.
- Egy víztározóban lévő víz: A magasabban lévő víz gravitációs potenciális energiával rendelkezik, amelyet a vízerőművek elektromos áram előállítására használnak fel.
- Egy fán lévő alma: Az almának a földfelszínhez viszonyított magassága miatt gravitációs potenciális energiája van. Amikor leesik, ez az energia mozgási energiává alakul.
Rugalmas Potenciális Energia
A rugalmas potenciális energia egy rugalmasan deformálható test (például egy rugó vagy egy gumiszalag) megfeszítéséből vagy összenyomásából származik. A rugalmas erővel szemben végzett munka tárolódik ebben az energiaformában. Egy ideális rugó rugalmas potenciális energiája a következőképpen adható meg:
\\mathbf\{E\_\{elas\} \= \\frac\{1\}\{2\}kx^2\}
ahol \(E_{elas}\) a rugalmas potenciális energia, \(k\) a rugóállandó (amely a rugó merevségét jellemzi), és \(x\) a rugó egyensúlyi helyzetétől való elmozdulása.
Példák a Rugalmas Potenciális Energiára
- Egy megfeszített rugó: Amikor egy rugót megfeszítünk vagy összenyomunk, rugalmas potenciális energiát tárol. Ez az energia szabadul fel, amikor a rugó visszatér eredeti alakjába.
- Egy kilőtt nyíl: A megfeszített íj húrjában tárolt rugalmas potenciális energia alakul át a nyíl kinetikus energiájává.
- Egy trambulin: Amikor valaki ráugrik a trambulinra, a rugók megfeszülnek, rugalmas potenciális energiát tárolva, amely aztán visszalökő erőt fejt ki.
A Mechanikai Energia Megmaradása
Az egyik legfontosabb elv a fizikában az energia megmaradásának törvénye, amely kimondja, hogy egy zárt rendszer teljes energiája állandó marad, feltéve, hogy nincsenek nem-konzervatív erők (például súrlódás vagy légellenállás) munkája. A mechanikai energia esetében ez azt jelenti, hogy egy olyan rendszerben, ahol csak konzervatív erők hatnak, a kinetikus energia és a potenciális energia összege állandó marad:
\\mathbf\{E\_\{mech\} \= E\_k \+ E\_p \= állandó\}
Példák az Energia Megmaradására
- Egy ingamozgás: Amikor az inga a legmagasabb pontján van, a potenciális energiája maximális, a kinetikus energiája pedig nulla. Ahogy az inga lefelé mozog, a potenciális energia kinetikus energiává alakul át. A legalacsonyabb ponton a kinetikus energia maximális, a potenciális energia pedig minimális. Ideális esetben a teljes mechanikai energia (a kinetikus és a potenciális energia összege) állandó marad.
- Egy leeső tárgy: Amikor egy tárgyat elejtünk, a kezdeti magasságban gravitációs potenciális energiával rendelkezik. Ahogy esik, ez az energia fokozatosan kinetikus energiává alakul át. Közvetlenül a földbe csapódás előtt a kinetikus energia maximális, a potenciális energia pedig minimális (a referencia szinttől függően).
Nem-Konzervatív Erők és a Mechanikai Energia Disszipációja
A valóságban gyakran vannak jelen nem-konzervatív erők, mint például a súrlódás és a légellenállás. Ezek az erők munkát végeznek a rendszeren, és ez a munka nem tárolódik potenciális energiaként, hanem általában hővé alakul. Ebben az esetben a teljes mechanikai energia nem marad meg, hanem csökken. Ezt az energiacsökkenést disszipációnak nevezzük.
Példák a Mechanikai Energia Disszipációjára
- Egy csúszó tárgy: Amikor egy tárgy egy felületen csúszik, a súrlódási erő munkát végez, és a mechanikai energia egy része hővé alakul, felmelegítve a tárgyat és a felületet. Ennek eredményeként a tárgy mozgása lelassul és végül megáll.
- Egy fékező autó: Az autó fékezése során a kinetikus energia a fékekben súrlódási hővé alakul, ami lelassítja az autót.
A Mechanikai Energia Átalakulásai
A mechanikai energia különböző formái egymásba alakulhatnak. Láttuk már a potenciális energia kinetikus energiává való átalakulását egy leeső tárgy vagy egy inga esetében, és fordítva, a kinetikus energia potenciális energiává alakulását egy felfelé dobott labda esetében, amely eléri a legmagasabb pontját.
További Példák az Energia Átalakulásaira
- Egy vízerőmű: A víztározóban lévő víz gravitációs potenciális energiája a turbinákon átfolyva kinetikus energiává alakul, amely aztán elektromos generátort hajt meg.
- Egy autó motorja: A benzin kémiai energiája először hővé, majd a mozgó alkatrészek révén mechanikai energiává alakul.
- Egy szélmalom: A szél kinetikus energiája a lapátokat forgatva mechanikai energiává alakul, amelyet aztán különböző célokra lehet felhasználni.
A Mechanikai Energia Jelentősége és Alkalmazásai
A mechanikai energia megértése és hasznosítása alapvető fontosságú számos tudományterületen és technológiai alkalmazásban.
Mérnöki Alkalmazások
- Gépészet: A gépek tervezése és működtetése a mechanikai energia átalakításán és továbbításán alapul.
- Építőmérnökség: Az épületek és hidak stabilitásának és a terhelések elviselésének megértéséhez elengedhetetlen a mechanikai erők és energiák ismerete.
- Repüléstechnika: A repülőgépek mozgása és a felhajtóerő létrehozása a mechanikai elveken alapul.

Mindennapi Élet
- A közlekedési eszközök (autók, vonatok, kerékpárok) mechanikai energiát használnak a mozgáshoz.
- A háztartási gépek (mosógép, turmixgép) működéséhez mechanikai energiára van szükség.
- A sporteszközök (labdák, ütők) használata során a mechanikai energia átalakulásai figyelhetők meg.
Összefoglalás
A mechanikai energia a mozgással és a helyzettel kapcsolatos energia. Két fő fajtája van: a kinetikus energia (a mozgás energiája) és a potenciális energia (a helyzetből adódó tárolt energia, amely lehet gravitációs vagy rugalmas). Egy zárt rendszerben, ahol csak konzervatív erők hatnak, a mechanikai energia megmarad. A valóságban azonban nem-konzervatív erők is jelen lehetnek, amelyek a mechanikai energia disszipációjához vezetnek. A mechanikai energia megértése kulcsfontosságú a természeti jelenségek és a technológiai alkalmazások széles körének megértéséhez.
További Tudnivalók a Mechanikai Energiáról
A mechanikai energia fogalmának mélyebb megértéséhez érdemes megvizsgálni a munka-energia tételt is, amely összekapcsolja a munkát és az energiaváltozást. A tétel kimondja, hogy egy testre ható összes erő által végzett munka egyenlő a test kinetikus energiájának megváltozásával:
\\mathbf\{W\_\{net\} \= \\Delta E\_k \= E\_\{k,f\} \- E\_\{k,i\}\}
ahol \(W_{net}\) a nettó munka, \(\Delta E_k\) a kinetikus energia változása, \(E_{k,f}\) a végső kinetikus energia, és \(E_{k,i}\) a kezdeti kinetikus energia.
A Konzervatív Erők és a Potenciális Energia Kapcsolata
A potenciális energia fogalma szorosan kapcsolódik a konzervatív erőkkel. Egy erő akkor konzervatív, ha az általa végzett munka egy zárt úton nulla, vagy ha a két pont között végzett munka független az útvonaltól. A gravitációs erő és a rugalmas erő tipikus példái a konzervatív erőknek. A potenciális energia definíció szerint a konzervatív erő által végzett munka negatívja:
\\mathbf\{\\Delta U \= \-W\_c\}
ahol \(\Delta U\) a potenciális energia változása, és \(W_c\) a konzervatív erő által végzett munka.
A Mechanikai Energia Mérésének Egységei
A mechanikai energiát (mind a kinetikus, mind a potenciális formában) a Nemzetközi Mértékegységrendszerben (SI) joule-ban (J) mérik. Egy joule egyenlő egy newton méterrel (N·m), vagy alapegységekben \(kg \cdot m^2/s^2\).
Komplexebb Rendszerek Mechanikai Energiája
Több testből álló rendszerek esetében a teljes mechanikai energia az egyes testek kinetikus és potenciális energiáinak összege. Például egy bolygórendszerben a bolygók kinetikus energiájának és a bolygók közötti gravitációs potenciális energiának az összege adja a rendszer teljes mechanikai energiáját.
Molekuláris szintű Mechanikai Energia
Bár a mechanikai energia fogalmát leggyakrabban makroszkopikus objektum
Mechanikai Energia Megmaradas Torvenye
A Mechanikai Energia Megmaradásának Törvénye: A Fizika Egyik Alapköve

A mechanikai energia megmaradásának törvénye a fizika egyik legfontosabb és legszélesebb körben alkalmazható alapelve. Kimondja, hogy egy izolált rendszerben, ahol csak konzervatív erők (mint például a gravitációs erő vagy a rugalmas erő) hatnak, a mechanikai energia – vagyis a kinetikus energia és a potenciális energia összege – időben állandó marad. Ez azt jelenti, hogy az energia nem vész el, hanem csak átalakul egyik formájából a másikba. Ebben a részletes cikkben mélyrehatóan megvizsgáljuk ezt a fundamentális törvényt, feltárjuk a mögötte rejlő elveket, szemléletes példákon keresztül mutatjuk be alkalmazásait, és megvitatjuk a nem konzervatív erők hatását is.
A Mechanikai Energia Definíciója és Összetevői
A mechanikai energia egy rendszer azon képessége, hogy munkát végezzen a mozgása vagy a helyzete miatt. Két fő összetevője van: a kinetikus energia és a potenciális energia. Ahhoz, hogy teljes mértékben megértsük a mechanikai energia megmaradásának törvényét, elengedhetetlen, hogy tisztában legyünk ezen összetevők definíciójával és jelentésével.
A Kinetikus Energia: A Mozgás Energiája
A kinetikus energia egy test mozgásából származó energia. Minél nagyobb egy test tömege és minél gyorsabban mozog, annál nagyobb a kinetikus energiája. Matematikailag a kinetikus energia (E\_k) a következőképpen fejezhető ki:
\\mathbf\{E\_k \= \\frac\{1\}\{2\}mv^2\}
ahol \\mathbf\{m\} a test tömege, \\mathbf\{v\} pedig a sebessége. Ebből az egyenletből is látható, hogy a kinetikus energia négyzetesen függ a sebességtől, ami azt jelenti, hogy a sebesség kétszeresére növelése négyszeresére növeli a kinetikus energiát. A tömeggel pedig egyenesen arányos, tehát kétszer akkora tömeg kétszer akkora kinetikus energiát jelent azonos sebesség mellett.
Gondoljunk csak egy guruló labdára, egy repülő repülőgépre vagy egy futó emberre. Mindegyik rendelkezik kinetikus energiával a mozgásuk miatt. Minél gyorsabban mozognak, annál nagyobb ez az energia. A kinetikus energia kulcsszerepet játszik számos fizikai jelenség megértésében, a mikroszkopikus részecskék mozgásától kezdve a bolygók pályájáig.
A Potenciális Energia: A Helyzetből Származó Energia
A potenciális energia egy test helyzetéből vagy konfigurációjából származó tárolt energia. Többféle formája létezik, attól függően, hogy milyen erőhatás eredményezi ezt az energiát. A mechanikában leggyakrabban a gravitációs potenciális energiával és a rugalmas potenciális energiával találkozunk.
Gravitációs Potenciális Energia
A gravitációs potenciális energia egy testnek a gravitációs térben elfoglalt helyzetéből adódik. A Föld felszínén, egy \\mathbf\{h\} magasságban lévő \\mathbf\{m\} tömegű test gravitációs potenciális energiája (E\_p) a következőképpen számítható ki:
\\mathbf\{E\_p \= mgh\}
ahol \\mathbf\{g\} a gravitációs gyorsulás (a Földön megközelítőleg 9\.81 \\, m/s^2). Ebből az egyenletből láthatjuk, hogy minél magasabbra emelünk egy testet, annál nagyobb lesz a gravitációs potenciális energiája. Ez az energia akkor szabadul fel, amikor a test leesik, és a potenciális energia kinetikus energiává alakul át.
Például egy hegy tetején álló kő nagyobb gravitációs potenciális energiával rendelkezik, mint egy a völgyben fekvő kő. Amikor a kő legurul a hegyről, ez a potenciális energia fokozatosan kinetikus energiává alakul át, miközben a magassága csökken.
Rugalmas Potenciális Energia
A rugalmas potenciális energia egy rugalmasan deformálható testben (például egy megnyújtott rugóban vagy egy meghajlított íjban) tárolt energia. Ha egy rugót \\mathbf\{x\} távolsággal megnyújtunk vagy összenyomunk a nyugalmi helyzetéhez képest, a benne tárolt rugalmas potenciális energia (E\_\{pr\}) a következőképpen adható meg:

\\mathbf\{E\_\{pr\} \= \\frac\{1\}\{2\}kx^2\}
ahol \\mathbf\{k\} a rugóállandó, amely a rugó merevségét jellemzi. Minél nagyobb a rugóállandó vagy a deformáció mértéke, annál nagyobb a tárolt rugalmas potenciális energia.
Egy megfeszített íjban tárolt rugalmas potenciális energia például arra használható fel, hogy egy nyilat nagy sebességgel kilőjön. Amikor az íj elengedik, a rugalmas potenciális energia kinetikus energiává alakul át, ami a nyilat repíti.
A Mechanikai Energia Megmaradásának Törvénye: A Kimondás és Magyarázat
Most, hogy megértettük a kinetikus és a potenciális energia fogalmát, rátérhetünk a mechanikai energia megmaradásának törvényére. Ahogy korábban említettük, ez a törvény azt állítja, hogy egy olyan izolált rendszerben, amelyre csak konzervatív erők hatnak, a mechanikai energia (a kinetikus és potenciális energia összege) állandó marad.
Matematikailag ezt a következőképpen fejezhetjük ki:
\\mathbf\{E\_\{mech\} \= E\_k \+ E\_p \= állandó\}
Vagyis, ha egy rendszer kezdeti állapotában a kinetikus energia E\_\{k1\} és a potenciális energia E\_\{p1\}, a mechanikai energia E\_\{mech1\} \= E\_\{k1\} \+ E\_\{p1\}. Egy későbbi időpontban, ha a kinetikus energia E\_\{k2\} és a potenciális energia E\_\{p2\}, akkor a mechanikai energia E\_\{mech2\} \= E\_\{k2\} \+ E\_\{p2\}. A megmaradás törvénye szerint:
\\mathbf\{E\_\{mech1\} \= E\_\{mech2\}\}
\\mathbf\{E\_\{k1\} \+ E\_\{p1\} \= E\_\{k2\} \+ E\_\{p2\}\}
Ez az egyenlet rendkívül hasznos problémák megoldásában, ahol energiatranszformációk történnek, de nincsenek nem konzervatív erők, amelyek energiát vonhatnak el a rendszerből (például súrlódás vagy légellenállás).
Konzervatív Erők vs. Nem Konzervatív Erők
A mechanikai energia megmaradásának törvénye szigorúan csak olyan rendszerekre érvényes, ahol a ható erők konzervatívak. Fontos megérteni a különbséget a konzervatív és a nem konzervatív erők között.
Konzervatív Erők
Egy erő akkor konzervatív, ha az általa végzett munka egy zárt úton nulla, vagy ha a két pont közötti munka független az úttól. A mechanikában a leggyakoribb konzervatív erők a gravitációs erő és a rugalmas erő. Amikor egy konzervatív erő munkát végez egy rendszeren, az energia potenciális energiaként tárolódik, és később visszanyerhető kinetikus energiaként (vagy más formában).
- Gravitációs erő: A gravitációs erő által végzett munka egy test felemelésekor megegyezik a gravitációs potenciális energia növekedésével. Amikor a test leesik, ez a potenciális energia kinetikus energiává alakul vissza.
- Rugalmas erő: Egy rugó megnyújtásakor vagy összenyomásakor a rugalmas erő munkát végez, amely rugalmas potenciális energiaként tárolódik. Amikor a rugó visszatér nyugalmi helyzetébe, ez az energia kinetikus energiává alakulhat.

Nem Konzervatív Erők
Egy erő akkor nem konzervatív, ha az általa végzett munka függ az úttól, és nem nulla egy zárt úton. A mechanikában a leggyakoribb nem konzervatív erők a súrlódási erő és a légellenállás. Amikor egy nem konzervatív erő munkát végez, az energia általában hővé alakul, és nem tér vissza a rendszer mechanikai energiájába.

- Súrlódási erő: Ha egy test egy felületen csúszik, a súrlódási erő munkát végez, amely hővé alakítja a mechanikai energiát (mind a test, mind a felület felmelegszik). Ez az energia nem nyerhető vissza mechanikai munkaként a rendszerben.
- Légellenállás: Egy levegőben mozgó testre ható légellenállási erő szintén nem konzervatív. Munkája hővé alakítja a mechanikai energiát és a levegő áramlásának energiájává.

A mechanikai energia megmaradásának törvénye csak akkor alkalmazható közvetlenül, ha a rendszerben ható összes erő konzervatív. Ha nem konzervatív erők is jelen vannak, akkor a rendszer teljes energiája (beleértve a hőenergiát is) marad meg, de a mechanikai energia önmagában nem feltétlenül állandó.
Példák a Mechanikai Energia Megmaradására
Számos klasszikus példa illusztrálja a mechanikai energia megmaradásának törvényét a gyakorlatban. Nézzünk meg néhányat részletesen:
Egy Szabadon Eső Test
Képzeljünk el egy \\mathbf\{m\} tömegű testet, amelyet egy \\mathbf\{h\} magasságból elejtünk. Kezdetben a test nyugalomban van, így a kinetikus energiája nulla (E\_\{k1\} \= 0), a potenciális energiája pedig E\_\{p1\} \= mgh. Tehát a kezdeti mechanikai energia E\_\{mech1\} \= 0 \+ mgh \= mgh.
Amint a test esni kezd, a gravitációs erő munkát végez rajta, és a potenciális energiája csökken, miközben a sebessége és ezzel együtt a kinetikus energiája nő. Egy tetszőleges \\mathbf\{y\} magasságban (ahol 0 \\le y \\le h), a potenciális energia E\_\{p2\} \= mgy. A sebességet ebben a pontban a következőképpen számíthatjuk ki a mozgásegyenletekből:
v^2 \= v\_0^2 \+ 2a\(h\-y\)

Mivel a kezdeti sebesség v\_0 \= 0 és a gyorsulás a \= g, ezért:
v^2 \= 2g\(h\-y\)
Így a kinetikus energia ebben a pontban:
E\_\{k2\} \= \\frac\{1\}\{2\}mv^2 \= \\frac\{1\}\{2\}m\(2g\(h\-y\)\) \= mg\(h\-y\)
A mechanikai energia ezen a ponton tehát:
E\_\{mech2\} \= E\_\{k2\} \+ E\_\{p2\} \= mg\(h\-y\) \+ mgy \= mgh
Láthatjuk, hogy E\_\{mech1\} \= E\_\{mech2\} \= mgh, ami azt bizonyítja, hogy a mechanikai energia megmarad a szabadesés során (feltételezve, hogy a légellenállás elhanyagolható).
A földetérés pillanatában (y \= 0), a potenciális energia nulla (E\_\{p3\} \= 0), a kinetikus energia pedig:
E\_\{k3\} \= mg\(h\-0\) \= mgh
Így a mechanikai energia ekkor is E\_\{mech3\} \= mgh \+ 0 \= mgh. Az egész folyamat során a gravitációs potenciális energia folyamatosan kinetikus energiává alakul át, de a kettő összege (a mechanikai energia) állandó marad.
Egy Ideális Ingamozgása
Tekintsünk egy ideális ingát, amely egy \\mathbf\{L\} hosszúságú, súlytalan fonálon függő \\mathbf\{m\} tömegű testből áll, és súrlódás nélkül leng. Amikor az inga a legmagasabb pontján van (valamelyik szélső helyzetben), pillanatnyi sebessége nulla, így a kinetikus energiája is nulla. Ebben a pontban a gravitációs potenciális energiája maximális, a legalacsonyabb ponthoz (egyensúlyi helyzethez) viszonyít
Mechanikai Energia Fogalma
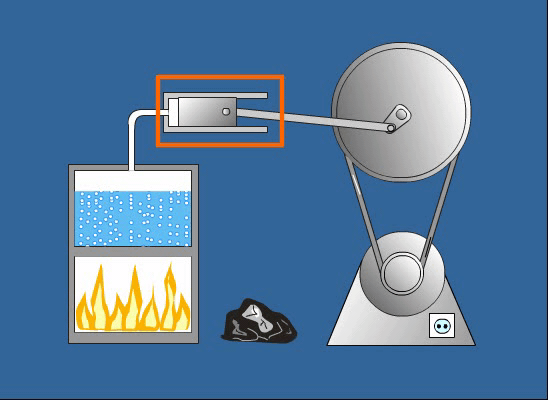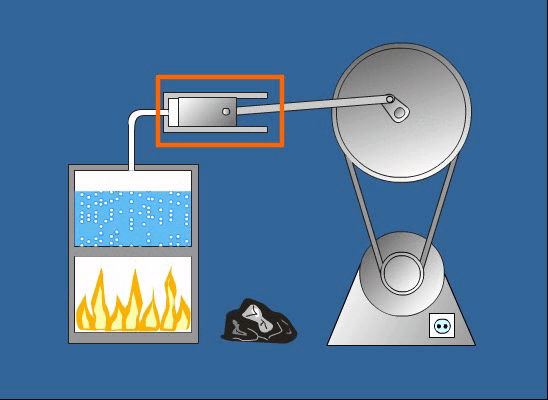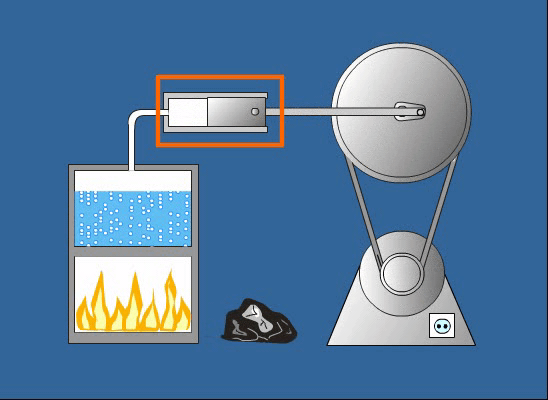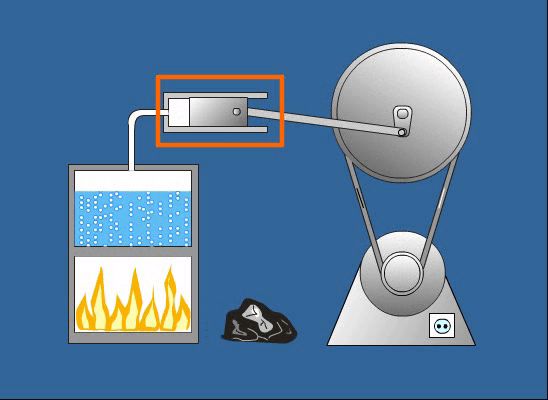
A Mechanikai Energia Fogalma: Átfogó Értelmezés és Alkalmazások
A mechanikai energia alapvető fogalom a fizikában és a mérnöki tudományokban, amely egy test vagy rendszer azon képességét írja le, hogy munkát végezzen a mozgásának vagy a helyzetének köszönhetően. Ez az energiaforma szorosan kapcsolódik a makroszkopikus objektumok mozgásához és kölcsönhatásaihoz, szemben például a termikus vagy elektromágneses energiával, amelyek a mikroszkopikus részecskék viselkedésével függnek össze. A mechanikai energia megértése kulcsfontosságú a fizikai jelenségek széles körének magyarázatához, a legegyszerűbb mozgásoktól kezdve a komplex gépek működéséig.
A Mechanikai Energia Két Fő Típusa
A mechanikai energiát alapvetően két fő összetevőre bonthatjuk: a kinetikus energiára és a potenciális energiára. Ezek az energiaformák szorosan összefüggenek, és egy mechanikai rendszer teljes energiája gyakran e kettő összegéből adódik.
A Kinetikus Energia: A Mozgás Energiája
A kinetikus energia egy test mozgásából származó energia. Minél nagyobb egy test tömege és minél nagyobb a sebessége, annál nagyobb a kinetikus energiája. Matematikailag a kinetikus energia ($E_k$) a következőképpen fejezhető ki:
$$\mathbf{E_k = \frac{1}{2}mv^2}$$
ahol $m$ a test tömege, $v$ pedig a sebessége.
Példák a Kinetikus Energiára a Mindennapi Életben
- Egy száguldó autó jelentős kinetikus energiával rendelkezik.
- Egy repülő labda szintén kinetikus energiával bír.
- A szél, mint mozgó levegő, képes munkát végezni a kinetikus energiájának köszönhetően (pl. szélmalmok forgatása).
- Egy folyó víz kinetikus energiája vízierőművekben hasznosítható.

A Kinetikus Energia Szerepe a Technikában
A kinetikus energia számos technológiai alkalmazás alapját képezi. Például a turbinák forgása, a járművek mozgása, és a különféle gépek működése mind a kinetikus energián alapulnak. A mérnökök gyakran törekednek a kinetikus energia hatékony átalakítására más energiaformákká, vagy éppen a mozgás létrehozására más energiaformákból.
A Potenciális Energia: A Helyzetből vagy Konfigurációból Származó Energia
A potenciális energia egy test vagy rendszer azon energiája, amely a helyzetéből vagy a konfigurációjából adódik. Számos formája létezik, attól függően, hogy milyen erőhatás áll a háttérben. A leggyakrabban említett típusok a gravitációs potenciális energia és a rugalmas potenciális energia.
Gravitációs Potenciális Energia
A gravitációs potenciális energia egy test azon energiája, amely a gravitációs térben elfoglalt helyzetéből adódik. Egy $h$ magasságban lévő, $m$ tömegű test gravitációs potenciális energiája ($E_p$) a következőképpen számítható ki a Föld felszínéhez képest:
$$\mathbf{E_p = mgh}$$
ahol $g$ a gravitációs gyorsulás.
Példák a Gravitációs Potenciális Energiára
- Egy hegy tetején lévő kő nagyobb gravitációs potenciális energiával rendelkezik, mint egy a völgyben lévő.
- Egy megfeszített íjban lévő nyíl rendelkezik gravitációs potenciális energiával, ha függőlegesen tartjuk.
- A víztározókban felgyülemlett víz jelentős gravitációs potenciális energiával rendelkezik, amelyet vízierőművek hasznosítanak.
Rugalmas Potenciális Energia
A rugalmas potenciális energia egy rugalmasan deformált testben tárolt energia. Ha egy rugót megnyújtunk vagy összenyomunk, munkát végzünk rajta, és ez a munka rugalmas potenciális energia formájában tárolódik. A rugalmas potenciális energia ($E_{rug}$) egy $x$-szel megnyújtott vagy összenyomott ideális rugó esetén a következőképpen adható meg:
$$\mathbf{E_{rug} = \frac{1}{2}kx^2}$$
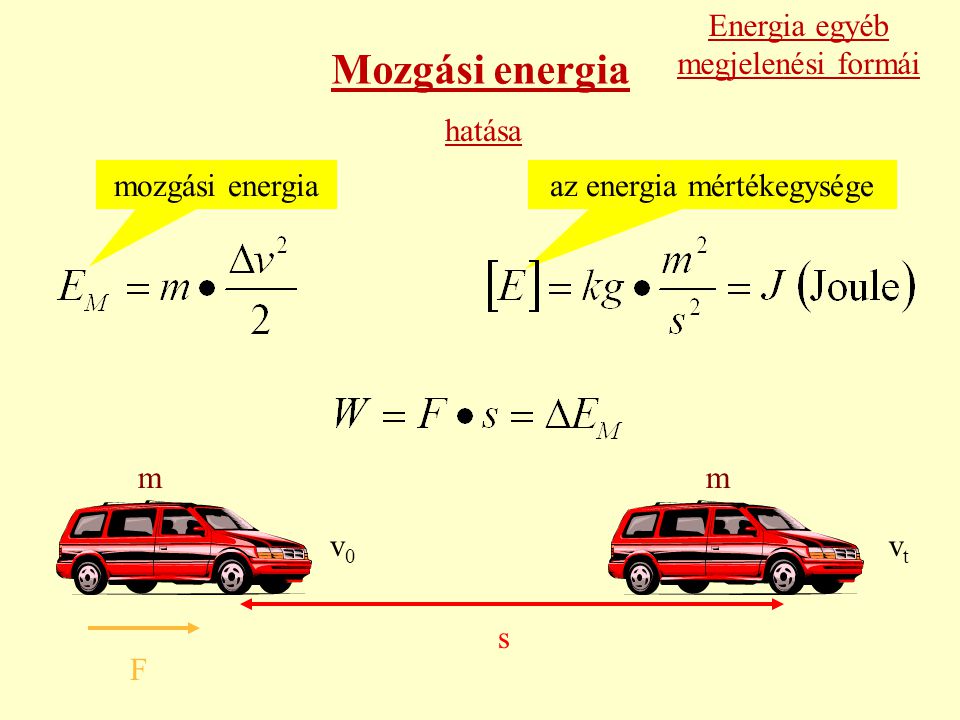
ahol $k$ a rugóállandó, $x$ pedig a rugó egyensúlyi helyzetétől való elmozdulása.
Példák a Rugalmas Potenciális Energiára
- Egy összenyomott rugó rugalmas potenciális energiával rendelkezik.
- Egy megfeszített gumiszalagban szintén rugalmas potenciális energia tárolódik.
- A trambulinra ugró ember a trambulin rugalmas deformációja révén rugalmas potenciális energiát halmoz fel.
Egyéb Formái a Potenciális Energiának
Bár a gravitációs és a rugalmas potenciális energia a leggyakrabban tárgyaltak, léteznek más formái is, mint például az elektromos potenciális energia (két elektromos töltés relatív helyzetéből adódó energia) és a mágneses potenciális energia (mágneses mezőben lévő mágneses dipólus energiája).
A Mechanikai Energia Megmaradásának Törvénye
A mechanikai energia megmaradásának törvénye az egyik legalapvetőbb elv a fizikában. Kimondja, hogy egy izolált rendszerben, ahol csak konzervatív erők (mint a gravitációs erő és az ideális rugóerő) hatnak, a mechanikai energia (a kinetikus és a potenciális energia összege) állandó marad. Matematikailag:
$$\mathbf{E_{mechanikai} = E_k + E_p = állandó}$$

Konzervatív és Nemkonzervatív Erők
A mechanikai energia megmaradása csak akkor érvényes, ha a rendszerben csak konzervatív erők hatnak. Egy erő akkor konzervatív, ha az általa végzett munka nem függ a megtett úttól, csak a kezdeti és a végső ponttól. A gravitációs erő és az ideális rugóerő példák konzervatív erőkre. Ezzel szemben a súrlódási erő egy nemkonzervatív erő, mert az általa végzett munka függ a megtett úttól, és a mechanikai energia egy része hővé alakul.
Példák a Mechanikai Energia Megmaradására
- Egy ingamozgása során a potenciális energia folyamatosan kinetikus energiává alakul át a legalacsonyabb ponton, majd vissza potenciális energiává a szélső pontokon. Ideális esetben (súrlódás nélkül) a teljes mechanikai energia megmarad.
- Egy leeső test gravitációs potenciális energiája fokozatosan kinetikus energiává alakul át, miközben a teljes mechanikai energia állandó marad (légellenállástól eltekintve).
- Egy rugóra akasztott test oszcillációja során a rugalmas potenciális energia és a kinetikus energia periodikusan átalakulnak egymásba, miközben a rendszer teljes mechanikai energiája megmarad.
A Mechanikai Energia Átalakulásai
A valóságban ritkán találkozunk tökéletesen izolált rendszerekkel, és gyakran nemkonzervatív erők is hatnak. Ilyen esetekben a mechanikai energia nem marad meg teljesen, hanem más energiaformákká alakulhat át, például hővé (a súrlódás miatt). Azonban az energia megmaradásának általános törvénye továbbra is érvényes: az energia nem vész el és nem keletkezik a semmiből, csak átalakul egyik formából a másikba.
Példák a Mechanikai Energia Átalakulására
- Egy fékező autóban a kinetikus energia a fékek súrlódása révén hővé alakul.
- Egy vízierőműben a víz gravitációs potenciális energiája először kinetikus energiává alakul a turbinák forgatásával, majd ez a kinetikus energia elektromos energiává alakul a generátorban.
- Egy égő gyufa kémiai energiát alakít át hővé és fényenergiává, de a súrlódással meggyújtott gyufa esetében a mozgás kinetikus energiája hővé alakul, ami beindítja a kémiai reakciót.


A Mechanikai Energia Szerepe a Technikában és a Mérnökségben
A mechanikai energia megértése és alkalmazása központi szerepet játszik a mérnöki tervezésben és a technológiai fejlesztésekben. Számos gép és eszköz működése a mechanikai energia különböző formáinak átalakításán és hasznosításán alapul.
Gépészet és Mechanikai Energia
A gépészet egyik fő területe a gépek tervezése, gyártása és működtetése, amelyek gyakran a mechanikai energiát használják fel munka végzésére. Ide tartoznak a motorok (amelyek kémiai vagy elektromos energiát alakítanak át mechanikai energiává), a hajtóművek (amelyek a mechanikai energia átvitelét és módosítását végzik), és a különféle munkagépek (amelyek a mechanikai energiát valamilyen hasznos feladatra fordítják).
Építőmérnökség és Mechanikai Energia
Az építőmérnököknek is figyelembe kell venniük a mechanikai energiával kapcsolatos jelenségeket, például a szél terhelését az épületekre (ami kinetikus energiával függ össze), vagy a földrengések hatásait (amelyek a föld mozgásából származó mechanikai energiát jelentik).
Energiatermelés és Mechanikai Energia
Számos energiatermelési módszer a mechanikai energia valamilyen formájának elektromos energiává alakításán alapul. A vízierőművek a víz gravitációs potenciális energiáját és kinetikus energiáját hasznosítják, a szélenergia a szél kinetikus energiáját, a hőerőművek pedig a gőz kinetikus energiáját forgatják meg a turbinákat.
Összefoglalás: A Mechanikai Energia Jelentősége
A mechanikai energia a fizika és a mérnöki tudományok egyik alapvető fogalma, amely a testek mozgásával és helyzetével kapcsolatos munkavégző képességét írja le. Két fő formája a kinetikus energia (a mozgás energiája) és a potenciális energia (a helyzetből vagy konfigurációból származó energia). A mechanikai energia megmaradásának törvénye alapvető elv a zárt rendszerekben, ahol csak konzervatív erők hatnak. A valóságban az energia gyakran átalakul más formákká, de az energia megmaradásának általános törvénye mindig érvényesül. A mechanikai energia megértése és alkalmazása nélkülözhetetlen a technológia és a mérnökség számos területén.
További Kapcsolódó Fogalmak
- Munka
- Teljesítmény
- Energiaátalakítás
- Hatásfok
Reméljük, hogy ez az átfogó cikk segített megérteni a mechanikai energia fogalmát és annak jelentőségét a természeti és a technikai világban. Ha további kérdései vannak, ne habozzon felvenni velünk a kapcsolatot!
Mechanikai Energia
A Mechanikai Energia Átfogó Értelmezése és Alkalmazásai
A mechanikai energia a fizika egyik alapvető fogalma, amely egy test vagy rendszer mozgásával és helyzetével kapcsolatos energiát írja le. Lényegében ez az az energia, amely lehetővé teszi a munkavégzést mechanikai úton. A mechanikai energia megértése kulcsfontosságú a klasszikus mechanika, a mérnöki tudományok és számos természeti jelenség magyarázatához. Ebben a részletes cikkben feltárjuk a mechanikai energia különböző aspektusait, beleértve annak definícióját, fajtáit, a megmaradás törvényét, az átalakulás folyamatait és a gyakorlati alkalmazásokat a mindennapi életben és a technológiában.
A Mechanikai Energia Definíciója és Alapelvei
A mechanikai energia egy rendszer azon képessége, hogy munkát végezzen. Ez magában foglalja a mozgással kapcsolatos energiát, amelyet kinetikus energiának nevezünk, és a helyzettel vagy konfigurációval kapcsolatos energiát, amelyet potenciális energiának hívunk. Egy mechanikai rendszer teljes energiája a kinetikus és potenciális energiájának összege, feltéve, hogy nincsenek disszipatív erők, mint például a súrlódás, amelyek hővé alakítják az energiát. A mechanikai energia szorosan kapcsolódik az erő és a mozgás fogalmaihoz, mivel az erők munkát végezhetnek, megváltoztatva egy test mozgását és ezáltal a mechanikai energiáját.

A Kinetikus Energia Részletes Bemutatása
A kinetikus energia egy mozgó test energiája. Minél nagyobb egy test tömege és sebessége, annál nagyobb a kinetikus energiája. Matematikailag a kinetikus energia (E\_k) a következőképpen fejezhető ki:
\\displaystyle E\_k \= \\frac\{1\}\{2\}mv^2

ahol m a test tömege (kilogrammban), és v a test sebessége (méter per másodpercben). Ebből az egyenletből látható, hogy a sebesség négyzetesen befolyásolja a kinetikus energiát, ami azt jelenti, hogy a sebesség kétszeresére növelése négyszeresére növeli a kinetikus energiát azonos tömeg mellett. A kinetikus energia skaláris mennyiség, ami azt jelenti, hogy csak nagysága van, iránya nincs.
Példák a Kinetikus Energiára a Mindennapi Életben
Számos példát találhatunk a kinetikus energiára a mindennapi életben. Egy guruló labda kinetikus energiával rendelkezik a mozgása miatt. Egy repülő repülőgép, egy futó ember vagy egy áramló víz mind rendelkezik kinetikus energiával. Minél gyorsabban mozognak, annál nagyobb a kinetikus energiájuk. A kinetikus energia hasznosítható is, például egy szélmalom a szél kinetikus energiáját alakítja át mechanikai munkává, amely aztán elektromos áramot termelhet.
A Potenciális Energia Részletes Bemutatása
A potenciális energia egy test vagy rendszer helyzetéből vagy konfigurációjából adódó tárolt energia. Többféle formája létezik, attól függően, hogy milyen erőhatás hozza létre. A mechanikában leggyakrabban a gravitációs potenciális energiával és a rugalmas potenciális energiával találkozunk.
Gravitációs Potenciális Energia
A gravitációs potenciális energia egy testnek a gravitációs mezőben elfoglalt helyzetéből adódik. A Föld felszínén egy h magasságban lévő m tömegű test gravitációs potenciális energiája (E\_p) a következőképpen számítható ki:

\\displaystyle E\_p \= mgh
ahol g a gravitációs gyorsulás (a Földön körülbelül 9\.81 \\, m/s^2). Ebből az egyenletből látható, hogy minél magasabban van egy test, annál nagyobb a gravitációs potenciális energiája egy adott referencia szinthez képest (általában a Föld felszíne). A gravitációs potenciális energia is skaláris mennyiség.
Példák a Gravitációs Potenciális Energiára
Egy hegy tetején álló kő gravitációs potenciális energiával rendelkezik a magassága miatt. Ha a kő leesik, ez a potenciális energia kinetikus energiává alakul át. Egy víztározóban felgyülemlett víz szintén gravitációs potenciális energiával rendelkezik, amelyet a vízerőművek elektromos áram termelésére használnak fel, amikor a vizet leengedik turbinákon keresztül.
Rugalmas Potenciális Energia
A rugalmas potenciális energia egy rugalmasan deformálódott testben tárolt energia, például egy megnyújtott vagy összenyomott rugóban. A rugalmas potenciális energia (E\_\{rug\}) egy ideális rugó esetében a következőképpen fejezhető ki (Hooke törvényéből származtatva):
\\displaystyle E\_\{rug\} \= \\frac\{1\}\{2\}kx^2
ahol k a rugóállandó (amely a rugó merevségét jellemzi), és x a rugó egyensúlyi helyzetétől való elmozdulása (megnyúlása vagy összenyomódása). A rugalmas potenciális energia is skaláris mennyiség.
Példák a Rugalmas Potenciális Energiára
Egy összenyomott rugó rugalmas potenciális energiával rendelkezik, amely felszabadulhat, ha a rugó kinyílik, például egy játékpisztolyban, amely egy golyót lő ki. Egy megfeszített íj húrjában is rugalmas potenciális energia tárolódik, amely a nyíl kilövéséhez szükséges kinetikus energiává alakul át.
A Mechanikai Energia Megmaradásának Törvénye
A mechanikai energia megmaradásának törvénye az egyik legalapvetőbb elv a fizikában. Kimondja, hogy egy izolált rendszerben, ahol csak konzervatív erők (mint a gravitáció és a rugalmas erő) hatnak, a rendszer teljes mechanikai energiája (a kinetikus és a potenciális energia összege) állandó marad az időben. Matematikailag ezt így fejezhetjük ki:
\\displaystyle E\_\{mechanikai\} \= E\_k \+ E\_p \= állandó
Ez azt jelenti, hogy az energia nem vész el és nem keletkezik, csak átalakulhat egyik formából a másikba. Például, amikor egy test leesik, a gravitációs potenciális energiája kinetikus energiává alakul át, de a kettő összege állandó (ha elhanyagoljuk a légellenállást).
Konzervatív és Nemkonzervatív Erők
A mechanikai energia megmaradásának törvénye csak akkor érvényes, ha a rendszerben ható erők konzervatívak. Egy erő akkor konzervatív, ha az általa végzett munka független az úttól, csak a kezdő- és végponttól függ. A gravitációs erő és a rugalmas erő példák konzervatív erőkre. Ezzel szemben a nemkonzervatív erők, mint a súrlódás vagy a légellenállás, olyan munkát végeznek, amely függ az úttól, és az általuk végzett munka nem téríthető vissza teljes mértékben más energiaformává (általában hővé alakul). Ha nemkonzervatív erők is jelen vannak, a rendszer teljes mechanikai energiája nem marad állandó, hanem csökkenhet.
Példa a Mechanikai Energia Megmaradására: A Lengőinga
Egy klasszikus példa a mechanikai energia megmaradására a lengőinga. Amikor az inga a legmagasabb pontján van, a sebessége nulla, így a kinetikus energiája is nulla, de a gravitációs potenciális energiája maximális. Ahogy az inga lefelé lendül, a potenciális energia kinetikus energiává alakul át, és a legalacsonyabb ponton a kinetikus energia maximális, míg a potenciális energia minimális (a választott referencia szinttől függően). Ha nem lenne légellenállás és súrlódás a felfüggesztési pontban, az inga örökké lengene, folyamatosan átalakítva a potenciális és kinetikus energiát egymásba, miközben a teljes mechanikai energia állandó maradna.
A Mechanikai Energia Átalakulásai
A mechanikai energia gyakran alakul át más energiaformákká és fordítva. Ahogy fentebb említettük, a potenciális energia kinetikus energiává alakulhat (például egy leeső tárgy esetében), és a kinetikus energia potenciális energiává (például egy felfelé dobott labda esetében, amely lelassul a legmagasabb pontján). Emellett a mechanikai energia átalakulhat hővé (például súrlódás következtében), hanggá (például egy ütközéskor) vagy akár elektromos energiává (például egy generátorban).
Példák a Mechanikai Energia Átalakulására
- Egy autó fékezésekor a mozgási energia (kinetikus energia) a fékekben hővé alakul át a súrlódás miatt.
- Egy vízerőműben a víz gravitációs potenciális energiája először a víz mozgási energiájává alakul át, majd a turbinák forgatásával mechanikai munkává, végül pedig egy generátor segítségével elektromos energiává.
- Amikor egy kalapáccsal egy szögbe ütünk, a kalapács mozgási energiája részben a szög mozgási energiájává és a fa deformálásához szükséges munkává alakul, emellett hő és hang is keletkezik.
- Egy trambulinon ugráló ember folyamatosan alakítja át a gravitációs potenciális energiát rugalmas potenciális energiává (a trambulin rugóiban vagy anyagában) és kinetikus energiává.


A Munka és a Mechanikai Energia Kapcsolata
A munka szorosan kapcsolódik a mechanikai energiához. A munka egy erő által végzett energiaátadás, amikor az erő elmozdít egy testet. Ha egy erő munkát végez egy testen, az megváltoztathatja a test mechanikai energiáját. A munka-energia tétel kimondja, hogy egy testre ható összes erő által végzett nettó munka egyenlő a test kinetikus energiájának megváltozásával:
\\displaystyle W\_\{nettó\} \= \\Delta E\_k \= E\_\{k,végső\} \- E\_\{k,kezdeti\}
Ha csak konzervatív erők végeznek munkát, akkor a teljes mechanikai energia megmarad, ami azt jelenti, hogy a kinetikus energia megváltozása egyenlő a potenciális energia negatív megváltozásával:
\\displaystyle \\Delta E\_k \= \-\\Delta E\_p
vagyis
\\displaystyle \\Delta \(E\_k \+ E\_p\) \= \\Delta E\_\{mechanikai\} \= 0
A Munka Számítása
A munka (W) egy állandó \\mathbf\{F\} erő által végzett munka, amely egy testet \\mathbf\{d\} vektorral elmozdít, a következőképpen számítható ki a skaláris szorzat segítségével:
\\displaystyle W \= \\mathbf\{F\} \\cdot \\mathbf\{d\} \= \|\\mathbf\{F\}\| \|\\mathbf\{d\}\| \\cos \\theta
ahol \|\\mathbf\{F\}\| az erő nagysága, \|\\mathbf\{d\}\| az elmozdulás nagysága, és \\theta az erő és az elmozdulás közötti szög. A munka mértékegysége a joule (J), amely megegyezik egy newton méterrel (N·m).
A Mechanikai Energia Gyakorlati Alkalmazásai
A mechanikai energia elvének megértése és alkalmazása számos technológiai és mérnöki területen elengedhetetlen. Néhány példa:
Energiatermelés
Sok energiatermelési módszer a mechanikai energia átalakításán alapul. A vízerőművek a víz gravitációs potenciális energiáját alakítják át először kinetikus energiává, majd mechanikai munkává a turbinák forgatásával, végül elektromos energiává a generátorokban. A szélenergia a szél kinetikus energiáját használja fel szélturbinák forgatására, ami mechanikai munkát végez, amelyet aztán elektromos árammá alakítanak. A hőerőművekben a hőenergia gőzt termel, amely turbinákat forgatva mechanikai energiát hoz létre, amit aztán elektromos árammá alakítanak.
Közlekedés
A közlekedési eszközök nagymértékben a mechanikai energiára támaszkodnak. A gépjárművek belső égésű motorjai vagy elektromos motorjai mechanikai munkát végeznek a kerekek forgatásához, ami mozgást eredményez. A repülőgépek hajtóművei tolóerőt generálnak, ami a repülőgép kinetikus energiájának növekedéséhez vezet. A vonatok elektromos vagy dízelmotorjai szintén mechanikai energiát használnak a mozgáshoz.
Gyártás és Ipari Folyamatok
A gyártásban és az ipari folyamatokban a mechanikai energia kulcsfontosságú a gépek működtetéséhez. Szerszámgépek, robotok és futószalagok mind mechanikai energiát használnak a feladatok elvégzéséhez. A hidraulikus és pneumatikus rendszerek folyadékok vagy gázok nyomását használják fel mechanikai munka végzésére.
Sport és Szórakozás
A mechanikai energia számos sportban és szórakozási formában is szerepet játszik. Egy labda eldobása vagy egy íjból kilőtt nyíl a testnek adott kinetikus energián alapul. A hullámvasutak a gravitációs potenciális energia és a kinetikus energia folyamatos átalakulásán alapulnak, izgalmas élményt nyújtva.
Összefoglalás
A mechanikai energia a mozgással és a helyzettel kapcsolatos energia, amely két fő formában létezik: kinetikus energia (a mozgás energiája) és potenciális energia (a helyzet vagy konfiguráció energiája). A mechanikai energia megmaradásának törvénye szerint egy izolált rendszer teljes mechanikai energiája állandó marad, ha csak konzervatív erők hatnak. A mechanikai energia folyamatosan átalakulhat más energiaformákká és fordítva, és szorosan kapcsolódik a munkához. A mechanikai energia elvének megértése elengedhetetlen a fizika, a mérnöki tudományok és számos gyakorlati alkalmazás szempontjából, az energiatermeléstől a közlekedésen át a gyártásig és a szórakozásig.
További Tanulási Lehetőségek
Kers Forma 1
A Forma 1 KERS Rendszere: A Kinetikus Energia Forradalma a Versenypályán
A Forma 1 világa folyamatosan fejlődik, a technológiai innovációk pedig elengedhetetlenek a versenyképesség megőrzéséhez. Az egyik legjelentősebb ilyen innováció a Kinetikus Energia Visszanyerő Rendszer, közismert nevén KERS. Ez a rendszer forradalmasította a versenyautók teljesítményét és a versenyzés dinamikáját azáltal, hogy lehetővé tette a fékezéskor felszabaduló energia visszanyerését és későbbi felhasználását.
Mi is pontosan a KERS? A Működés Részletei
A KERS egy olyan hibrid rendszer, amelynek célja a versenyautó mozgási energiájának (kinetikus energiájának) visszanyerése a fékezési fázisban. A hagyományos fékrendszerek ezt az energiát hővé alakítják, ami aztán elveszik a környezet számára. A KERS ezzel szemben ezt az energiát elektromos formában tárolja, majd a pilóta egy gombnyomással ideiglenesen felhasználhatja a gyorsítás érdekében.
A KERS Főbb Komponensei és Működési Elve
A KERS rendszer alapvetően három fő részből áll:

- Motor-generátor egység (MGU-K): Ez az egység felelős a kinetikus energia visszanyeréséért a fékezés során, valamint az eltárolt energia visszaadásáért a hajtásláncba. Az MGU-K általában a motor és a sebességváltó között helyezkedik el.
- Akkumulátor (vagy szuperkondenzátor): Ez az egység tárolja az MGU-K által visszanyert elektromos energiát. Az akkumulátorok vagy szuperkondenzátorok közötti választás a energiasűrűség és a teljesítménysűrűség közötti kompromisszumot tükrözi.
- Vezérlő elektronika: Ez a rendszer felügyeli az energia visszanyerését, tárolását és leadását, biztosítva a rendszer optimális működését és a szabályozások betartását.
A Kinetikus Energia Visszanyerésének Folyamata
Amikor a pilóta fékezni kezd, az MGU-K generátorként működik. A kerekek lassulása által generált forgási energia az MGU-K-n keresztül elektromos energiává alakul. Ez az elektromos energia aztán az akkumulátorban vagy a szuperkondenzátorban tárolódik későbbi felhasználásra.
Az Eltárolt Energia Felhasználása
A pilóta egy kormányon elhelyezett gomb megnyomásával aktiválhatja a KERS rendszert. Ekkor az akkumulátorban vagy szuperkondenzátorban tárolt elektromos energia az MGU-K-t motorként hajtja meg, amely kiegészítő teljesítményt biztosít a hajtáslánc számára. Ez a többletteljesítmény kritikus lehet az előzéshez, a védekezéshez vagy a köridő javításához.
A KERS Története a Forma 1-ben: A Bevezetés és a Fejlődés
A KERS rendszert először a 2009-es Forma 1-es szezonban vezették be. Bár a kezdeti implementáció nem volt kötelező, több csapat is élt a lehetőséggel, hogy előnyt szerezzen a technológia alkalmazásával. A rendszer bevezetése jelentős lépés volt a Forma 1 számára a fenntarthatóbb és technológiailag fejlettebb motorsport irányába.
A 2009-es Szezon: A KERS Debütálása
A 2009-es szezonban olyan csapatok használtak KERS-t, mint a Ferrari, a McLaren, a BMW Sauber, a Renault és a Williams. A kezdeti időszakban a technológia megbízhatósága és integrációja kihívásokat jelentett, de a potenciális előnyök nyilvánvalóak voltak. Például Lewis Hamilton a McLarennel megnyerte a Magyar Nagydíjat, ahol a KERS kulcsszerepet játszott az előzéseiben.
A KERS Evolúciója: A Szabályozások Változása
Az évek során a Forma 1 szabályozói finomították a KERS-re vonatkozó előírásokat. A kezdeti korlátozások után a rendszer egyre kiforrottabbá és elterjedtebbé vált. A 2014-es szezonban a hibrid hajtásláncok bevezetésével a KERS szerepe még hangsúlyosabbá vált, integrálódva az összetettebb energia-visszanyerő rendszerekbe.
A KERS Előnyei és Hátrányai a Forma 1-ben
Mint minden technológiai újításnak, a KERS-nek is vannak előnyei és hátrányai a Forma 1 kontextusában.
A KERS Előnyei
- Növelt teljesítmény: A KERS lehetővé teszi a pilóták számára, hogy ideiglenesen extra teljesítményhez jussanak, ami kulcsfontosságú lehet az előzéshez és a védekezéshez.
- Stratégiai előny: A KERS felhasználása stratégiai szempontból is fontos lehet, például a rajtnál, a kigyorsításoknál vagy a kritikus pillanatokban.
- Technológiai fejlesztés: A Forma 1 a KERS-en keresztül a hibrid technológiák fejlesztésének élvonalában jár, ami a közúti autók fejlesztésére is hatással lehet.
- Fenntarthatóság: Az energia visszanyerése hozzájárul a versenyzés ökológiai lábnyomának csökkentéséhez, bár a fő cél a teljesítmény növelése.
A KERS Hátrányai
- Súlytöbblet: A KERS rendszere, beleértve az akkumulátort és az MGU-K-t, extra súlyt jelent az autó számára, ami befolyásolhatja a kezelhetőséget.
- Komplexitás és költség: A KERS egy komplex és költséges rendszer, amely növeli az autók gyártási és karbantartási költségeit.
- Megbízhatósági problémák: A kezdeti időkben a KERS megbízhatósági problémákkal küzdött, ami kiesésekhez vezethetett. Bár ezek a problémák nagyrészt megoldódtak, a komplex rendszerek mindig magukban hordozzák a meghibásodás kockázatát.
- Szabályozási korlátok: A szabályozások korlátozzák a KERS által leadható energia mennyiségét és idejét, ami befolyásolja a rendszer stratégiai alkalmazását.
A KERS Műszaki Részletei: Mélyebbre Ásunk

A KERS rendszer műszaki megértése elengedhetetlen a technológia teljes körű megértéséhez.
A Motor-Generátor Egység (MGU-K)
Az MGU-K egy elektromos gép, amely kettős funkciót lát el: generátorként működik a fékezés során, elektromos energiát termelve, és motorként működik az eltárolt energia visszaadásakor. Az MGU-K általában egy nagy sebességű, kefe nélküli elektromos motor, amely közvetlenül a hajtáslánchoz kapcsolódik. A hatékonyság maximalizálása érdekében az MGU-K fordulatszáma gyakran a motor fordulatszámához igazodik áttételeken keresztül.
Az Energiatároló Rendszer: Akkumulátorok és Szuperkondenzátorok
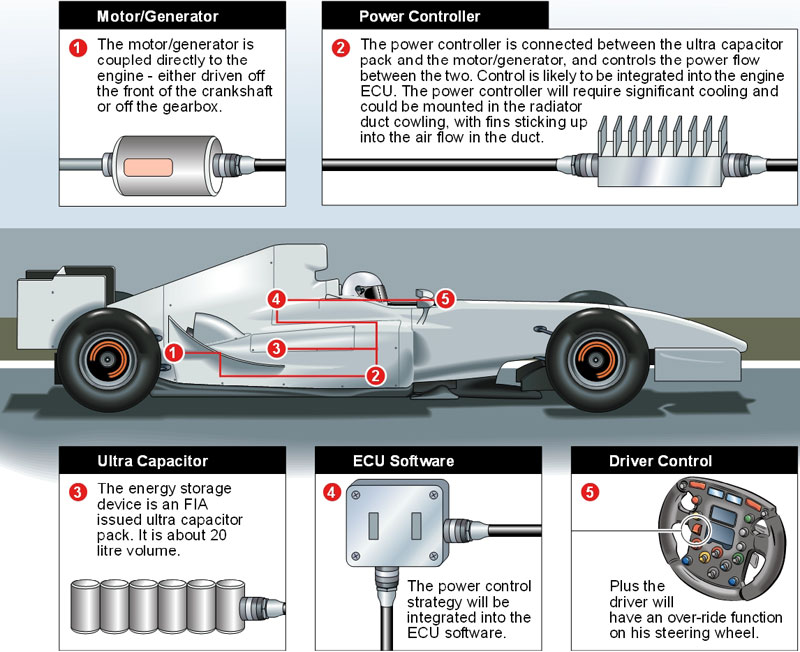
Az energiatárolásra két fő technológiát alkalmaztak a Forma 1-ben: akkumulátorokat és szuperkondenzátorokat.
Akkumulátorok
Az akkumulátorok kémiai reakciók révén tárolják az energiát. Nagy energiasűrűségük miatt képesek nagyobb mennyiségű energiát tárolni, de a töltési és kisütési sebességük általában alacsonyabb, mint a szuperkondenzátoroké.
Szuperkondenzátorok
A szuperkondenzátorok elektrosztatikus elven tárolják az energiát. Kisebb az energiasűrűségük, de sokkal gyorsabban képesek feltöltődni és kisülni, ami ideális a rövid ideig tartó, nagy teljesítményű energiaigények kielégítésére, mint amilyen a KERS aktiválása.
A Forma 1-ben a kezdeti rendszerek gyakran akkumulátorokat használtak, de a technológia fejlődésével a szuperkondenzátorok is elterjedtek a gyorsabb energiaátvitel képességük miatt.
A Vezérlő Elektronika Szerepe
A KERS vezérlő elektronikája kulcsfontosságú a rendszer biztonságos és hatékony működéséhez. Ez a rendszer felügyeli az energia visszanyerésének mértékét, az akkumulátor vagy szuperkondenzátor töltöttségi szintjét, valamint az energia leadásának időzítését és mértékét. A modern vezérlő rendszerek rendkívül kifinomultak, és valós időben optimalizálják a KERS működését a pilóta utasításai és a versenypálya körülményei alapján.
A KERS Hatása a Forma 1 Versenyzésére
A KERS bevezetése jelentős hatással volt a Forma 1 versenyzésére, mind a taktikai, mind a technikai szempontból.
Taktikai Alkalmazások
A pilóták a KERS-t számos taktikai célra használhatják:
- Előzés: A KERS által biztosított extra teljesítmény kritikus lehet az előzési manőverek végrehajtásához, különösen a kigyorsításoknál a kanyarokból.
- Védekezés: A pilóták a KERS segítségével megvédhetik pozíciójukat a támadókkal szemben, növelve a kigyorsításukat a kritikus szakaszokon.
- Rajt: A rajtnál a KERS azonnali teljesítménynövelést biztosít, ami segíthet a jobb pozíció megszerzésében az első kanyarig.
- Köridő javítás: Bizonyos pályaszakaszokon a KERS stratégiai használatával javítani lehet a köridőt, különösen az egyenesekben.

Technikai Kihívások és Megoldások
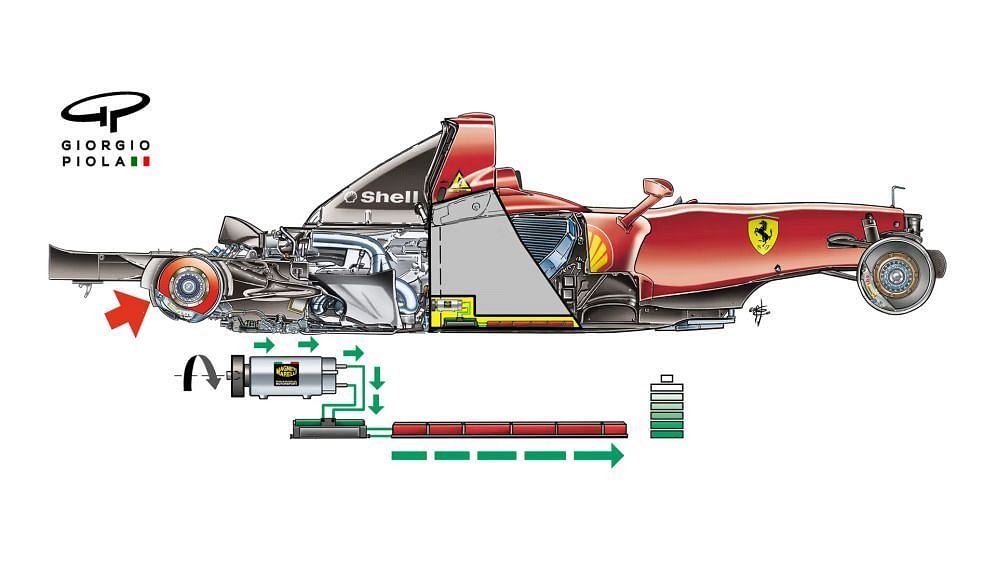
A KERS bevezetése számos technikai kihívást is jelentett a csapatok számára:
- Hűtés: Az elektromos alkatrészek, különösen az akkumulátor vagy szuperkondenzátor, hatékony hűtést igényelnek a túlmelegedés elkerülése érdekében.
- Súlyelosztás: A KERS alkatrészeinek elhelyezése befolyásolja az autó súlyelosztását, ami hatással van a kezelhetőségre. A csapatoknak optimalizálniuk kellett az alkatrészek elhelyezését a legjobb egyensúly elérése érdekében.
- EMI (elektromágneses interferencia): Az elektromos rendszerek interferenciát okozhatnak az autó más elektronikus rendszereivel. A megfelelő árnyékolás és szűrés elengedhetetlen a problémák elkerüléséhez.
- Biztonság: A nagyfeszültségű elektromos rendszerek biztonsági kockázatot jelenthetnek baleset esetén. A Forma 1 szigorú biztonsági előírásokat vezetett be a KERS rendszerekre vonatkozóan.
A Jövő: A KERS és az Energia-Visszanyerő Rendszerek Evolúciója
A Forma 1 továbbra is a hibrid technológiák élvonalában jár, és a KERS-ből kifejlődött komplexebb energia-visszanyerő rendszerek (ERS) kulcsszerepet játszanak a modern versenyautók teljesítményében.
Az ERS Rendszerek: Több Mint KERS
A jelenlegi Forma 1-es autók nem csupán KERS-sel rendelkeznek, hanem egy sokkal összetettebb ERS rendszerrel, amely két motor-generátor egységet foglal magában:
- MGU-K (Motor Generator Unit – Kinetic): Hasonló a korábbi KERS-hez, a fékezés során nyer vissza energiát.
- MGU-H (Motor Generator Unit – Heat): A turbófeltöltő kipufogógázából származó hőenergiát alakítja elektromos energiává. Ez az energia tárolható, vagy közvetlenül felhasználható az MGU-K-n keresztül a hajtáslánc támogatására.
Ez a komplexebb rendszer lehetővé teszi a még hatékonyabb energia-visszanyerést és -felhasználást, tovább növelve a hibrid hajtásláncok jelentőségét a Forma 1-ben.
A Fenntarthatóság Felé: A Hibrid Technológia Jövője
A Forma 1 elkötelezett a fenntarthatóság növelése mellett, és a hibrid technológiák kulcsszerepet játszanak ebben a törekvésben. A jövőben várhatóan még nagyobb hangsúlyt kap az energiahatékonyság és a fenntartható üzemanyagok használata, ami tovább fogja formálni az energia-visszanyerő rendszerek fejlődését.
Összegzés: A KERS Öröksége a Forma 1-ben
A Kinetikus Energia Visszanyerő Rendszer (KERS) bevezetése mérföldkő volt a Forma 1 történetében. Nemcsak a versenyautók teljesítményét növelte, hanem elindított egy technológiai forradalmat, amely a mai komplex hibrid hajtásláncokhoz vezetett. A KERS megmutatta, hogy az energia visszanyerése és intelligens felhasználása kulcsfontosságú lehet a motorsport legmagasabb szintjén, és inspirációt adott a közúti autók hibrid technológiáinak fejlődéséhez is. A KERS öröksége továbbra is él a modern Forma 1-ben, ahol az energia-visszanyerő rendszerek a versenyképesség alapvető elemét képezik.