Energiamegmaradas Elve

Az Energiamegmaradás Elve: A Természet Alapvető Törvénye

Az energiamegmaradás elve a fizika egyik legfontosabb és legalapvetőbb törvénye. Kimondja, hogy egy zárt rendszer teljes energiája időben állandó marad. Ez azt jelenti, hogy az energia nem keletkezhet a semmiből és nem veszhet el, csupán egyik formából a másikba alakulhat át. Ez az elv áthatja a természettudományok minden területét, a mechanikától a termodinamikán át az elektromágnességig és a részecskefizikáig. Megértése elengedhetetlen a természeti jelenségek helyes értelmezéséhez és a technológiai fejlesztésekhez.

Az Energiamegmaradás Elvének Formális Megfogalmazása

Formálisan az energiamegmaradás elvét a következőképpen fogalmazhatjuk meg: egy izolált rendszer teljes energiája állandó. Matematikailag ezt gyakran a következőképpen írjuk le:

$$\Delta E_{rendszer} = 0$$

Ahol $\Delta E_{rendszer}$ a rendszer teljes energiájának megváltozását jelöli. Ez azt jelenti, hogy ha a rendszer izolált (azaz nem cserél energiát a környezetével), akkor a benne lévő összes energia mennyisége nem változik meg. Az energia azonban átalakulhat különböző formák között, mint például kinetikus energia (mozgási energia), potenciális energia (helyzeti energia), hőenergia, elektromágneses energia, kémiai energia és nukleáris energia.

A Zárt és Izolált Rendszerek Fogalma

Fontos megkülönböztetni a zárt és az izolált rendszereket. Egy zárt rendszer olyan rendszer, amely nem cserél anyagot a környezetével, de energiát igen. Ezzel szemben egy izolált rendszer sem anyagot, sem energiát nem cserél a környezetével. Az energiamegmaradás elve szigorúan véve izolált rendszerekre vonatkozik. A valóságban tökéletesen izolált rendszerek nem léteznek, de sok esetben egy rendszer jó közelítéssel izoláltnak tekinthető egy adott időtartamra.

Példa zárt rendszerre

Egy lezárt edényben lévő gáz zárt rendszernek tekinthető, mert a gáz molekulái nem jutnak ki az edényből, de hő formájában energia cserélődhet az edény fala és a környezet között.

Példa (közelítőleg) izolált rendszerre

Egy jól szigetelt termoszban lévő forró kávé egy bizonyos ideig jó közelítéssel izolált rendszernek tekinthető, mivel mind az anyag (a kávé), mind az energia (hő) cseréje a környezettel minimális.

Az Energia Különböző Formái és Átalakulásuk

Az energia számos különböző formában létezhet, és ezek a formák egymásba alakulhatnak az energiamegmaradás elvének megfelelően.

Kinetikus Energia

A kinetikus energia egy test mozgásából származó energia. Egy $m$ tömegű, $v$ sebességgel mozgó test kinetikus energiája a következőképpen számítható:

$$E_k = \frac{1}{2}mv^2$$

Amikor egy tárgy sebessége megváltozik, a kinetikus energiája is megváltozik. Például, amikor egy autó gyorsul, a kinetikus energiája nő, mivel a sebessége nő. Ez az energia a motor által végzett munka révén kerül a rendszerbe, ami végső soron a benzin kémiai energiájából származik.

Potenciális Energia

A potenciális energia egy test helyzetéből vagy konfigurációjából származó tárolt energia. Többféle potenciális energia létezik:

Gravitációs potenciális energia

Egy $m$ tömegű, a Föld felszínétől $h$ magasságban lévő test gravitációs potenciális energiája a következőképpen számítható (feltételezve, hogy $h$ sokkal kisebb, mint a Föld sugara, és a gravitációs gyorsulás ($g$) állandó):

$$E_p = mgh$$

Amikor egy tárgy leesik, a gravitációs potenciális energiája kinetikus energiává alakul. Az energiamegmaradás elve ebben az esetben azt jelenti, hogy a kezdeti potenciális energia (a magasban) egyenlő a végső kinetikus energiával (a földet érés pillanatában), ha nem veszítünk energiát más formákban (pl. légellenállás).

Rugalmas potenciális energia

Egy megnyújtott vagy összenyomott rugó rugalmas potenciális energiával rendelkezik. Ha egy rugó $x$ távolsággal van kitérítve a nyugalmi helyzetéből, akkor a rugalmas potenciális energiája a következőképpen számítható (Hooke-törvényét feltételezve):

$$E_{rugalmas} = \frac{1}{2}kx^2$$

Ahol $k$ a rugóállandó. Amikor egy rugó elengedik, a rugalmas potenciális energia kinetikus energiává alakulhat, vagy munkát végezhet más testeken.

Hőenergia (Termikus Energia)

A hőenergia egy rendszer belső energiájának egy része, amely az atomok és molekulák véletlenszerű mozgásával kapcsolatos. Minél nagyobb a rendszer hőmérséklete, annál nagyobb az atomok és molekulák átlagos kinetikus energiája, és így annál nagyobb a hőenergiája. A hőenergia átadható egyik rendszerről a másikra hő formájában (vezetés, áramlás, sugárzás).

Elektromágneses Energia

Az elektromágneses energia az elektromos és mágneses mezőkkel kapcsolatos energia. Ide tartozik a fény, a rádióhullámok, a mikrohullámok, az infravörös és az ultraibolya sugárzás, a röntgensugárzás és a gammasugárzás. Ezek az energiák képesek terjedni a vákuumban is. Az elektromágneses energia kölcsönhatásba léphet a töltött részecskékkel, és energiát adhat át nekik.

Kémiai Energia

A kémiai energia az atomokat és molekulákat összetartó kémiai kötésekben tárolt energia. Kémiai reakciók során ezek a kötések felbomolhatnak vagy új kötések jöhetnek létre, ami energia felszabadulásával (exoterm reakció) vagy energiafelvétellel (endoterm reakció) járhat. Például az égés során a kémiai energia hő- és fényenergiává alakul.

Nukleáris Energia

A nukleáris energia az atommagban tárolt energia, amely az atommagot alkotó nukleonok (protonok és neutronok) közötti erős kölcsönhatásból származik. Nukleáris reakciók, mint például a maghasadás (fisszió) vagy a magfúzió (fúzió), hatalmas mennyiségű nukleáris energiát szabadíthatnak fel.

Az Energiamegmaradás Elvének Alkalmazásai

Az energiamegmaradás elvének számos fontos alkalmazása van a tudományban és a mérnöki gyakorlatban.

Mechanika

A mechanikában az energiamegmaradás elve segít megérteni a mozgást és a kölcsönhatásokat. Például egy inga mozgása során a gravitációs potenciális energia folyamatosan kinetikus energiává alakul és fordítva, miközben a teljes mechanikai energia (a kinetikus és a potenciális energia összege) állandó marad (ideális esetben, súrlódás nélkül).

Példa: Az egyszerű inga

Egy $m$ tömegű, $L$ hosszúságú fonálon függő inga kezdetben $\theta$ szögben van kitérítve. Amikor elengedjük, a gravitációs potenciális energiája csökken, miközben a kinetikus energiája nő. A legalacsonyabb ponton a potenciális energia minimális, a kinetikus energia pedig maximális. Az energiamegmaradás elve alapján:

$$mgh_{kezdeti} = \frac{1}{2}mv_{legalsó}^2$$

Ahol $h_{kezdeti} = L(1 – \cos\theta)$ a kezdeti magasság, és $v_{legalsó}$ a legalacsonyabb ponton lévő sebesség.

Termodinamika

A termodinamika első főtétele az energiamegmaradás elvének egy speciális megfogalmazása termodinamikai rendszerekre. Kimondja, hogy egy zárt rendszer belső energiájának ($\Delta U$) megváltozása egyenlő a rendszerrel közölt hő ($Q$) és a rendszeren végzett munka ($W$) összegével:

$$\Delta U = Q – W$$

Ez az egyenlet azt fejezi ki, hogy az energia nem vész el és nem keletkezik, csak átalakulhat hővé vagy munkává, és megváltoztathatja a rendszer belső energiáját.

Példa: Gáz expanziója

Ha egy gáz egy hengerben expandál, munkát végez a dugattyún. Ha közben hőt adunk a gázhoz, akkor a belső energiája is megváltozhat. A termodinamika első főtétele segít számszerűsíteni ezeket az energiaátalakulásokat.

Elektromágnesség

Az elektromágnességben az energiamegmaradás elve megnyilvánul például az elektromágneses mező energiájában. Egy elektromos mező és egy mágneses mező energiát tárolhat, és ez az energia átalakulhat más formákká, például a töltött részecskék mozgási energiájává vagy hővé (Joule-hő).

Példa: Kondenzátor kisülése

Egy feltöltött kondenzátor elektromos energiát tárol az elektromos mezőjében. Amikor egy ellenálláson keresztül kisül, ez az energia hővé alakul az ellenállásban (Joule-effektus). Az energiamegmaradás elve azt mondja ki, hogy a kondenzátor kezdeti elektromos energiája egyenlő az ellenálláson disszipált hőenergiával.

Relativitáselmélet és az Energia-Tömeg Ekvivalencia

Einstein speciális relativitáselmélete egy mély kapcsolatot tárt fel az energia és a tömeg között. Az híres $E=mc^2$ egyenlet kimondja, hogy az energia ($E$) és a tömeg ($m$) ekvivalensek egymással, ahol $c$ a fény sebessége vákuumban. Ez azt jelenti, hogy a tömeg az energia egy formája, és az energia tömeggé alakulhat, és fordítva. A relativisztikus energiamegmaradás elve szerint egy zárt rendszer teljes relativisztikus energiája (amely magában foglalja a nyugalmi energiát $mc^2$-t is) megmarad.

Példa: Atomreakciók

Az atomreakciókban, mint például a maghasadás vagy a magfúzió, a tömeg egy kis része energiává alakul át az $E=mc^2$ egyenlet szerint, ami hatalmas mennyiségű energia felszabadulásához vezet.

Az Energiamegmaradás Elvének Kísérleti Bizonyítékai

Az energiamegmaradás elvét számtalan kísérlet és megfigyelés támasztja alá a fizika, a kémia és más természettudományok területén. Soha nem találtak olyan jelenséget, amely egyértelműen megszegné ezt az elvet. Ezért tekintjük az egyik legszilárdabb és legáltalánosabb természeti törvénynek.

A Joule-kísérlet

James Prescott Joule híres kísérletei a 19. század közepén fontos bizonyítékot szolgáltattak a mechanikai munka és a hő közötti ekvivalenciára, ami az energiamegmaradás elvének egyik korai megerősítése volt. Joule megmutatta, hogy egy adott mennyiségű mechanikai munka mindig ugyanannyi hőt termel, függetlenül attól, hogyan végezzük a munkát.

Elektromágneses indukció

Faraday elektromágneses indukciós kísérletei megmutatták, hogy a változó mágneses mező elektromos mezőt hoz létre, és fordítva. Ezek a jelenségek az elektromágneses energia átalakulását és megmaradását tükrözik.

Atom- és magfizikai kísérletek

Az atom- és magfizikai kísérletek során végzett precíz mérések is megerősítették az energiamegmaradás elvét, beleértve a relativisztikus formáját is. Az elemi részecskék kölcsönhatásai és az atommagok átalakulásai során a teljes energia (beleértve a tömegenergiát is) mindig megmarad.

Az Energiamegmaradás Elvének Filozófiai Jelentősége

Az energiamegmaradás elvének nem csak tudományos, hanem filozófiai jelentősége is van. Azt sugallja, hogy a világban van valami állandó és megőrződő, még akkor is, ha minden látszólag változik. Ez az elv hozzájárul a természet egységének és koherenciájának megértéséhez.

A megmaradási törvények szerepe a fizikában

Az energiamegmaradás elve csak egy a sok megmaradási törvény közül a fizikában. Hasonlóan fontos a lendületmegmaradás, a tömegmegmaradás (klasszikus fizikában), a töltésmegmaradás és más megmaradási törvények. Ezek a törvények alapvető szimmetriákkal állnak kapcsolatban a tér, az idő és más fizikai mennyiségek tekintetében (Noether-tétel).

Összefoglalás

Az energiamegmaradás elve a természet egyik legmélyebb és legáltalánosabb törvénye. Kimondja, hogy egy izolált rendszer teljes energiája állandó. Az energia különböző formákban létezhet (kinetikus, potenciális, hő, elektromágneses, kémiai, nukleáris), és ezek a formák egymásba alakulhat

Mechanikai Energia Feladatok

Mechanikai Energia Feladatok: Átfogó Gyakorlatok és Megoldások a Sikeres Tanuláshoz

Üdvözöljük a mechanikai energia világában! Ez az átfogó útmutató részletes feladatokon keresztül segít elmélyíteni a kinetikus energia, a potenciális energia, a munka fogalmát és az energiamegmaradás törvényét. Célunk, hogy a legbonyolultabbnak tűnő feladatokat is érthetővé és megoldhatóvá tegyük. Készüljön fel, hogy elsajátítsa a mechanikai energia alapelveit!

A Mechanikai Energia Alapjai: Kinetikus és Potenciális Energia

A mechanikai energia egy rendszer mozgásával vagy helyzetével kapcsolatos energia. Két fő formája létezik: a kinetikus energia, amely a mozgásból származik, és a potenciális energia, amely a test helyzetéből vagy konfigurációjából adódik. Mindkét fogalom kulcsfontosságú a fizikai problémák megértéséhez és megoldásához.

Kinetikus Energia: A Mozgás Energiája

A kinetikus energia (\\\(E\_k\\\)) egy test mozgásának köszönhető energia. Minél nagyobb egy test tömege és sebessége, annál nagyobb a kinetikus energiája. A kinetikus energia képlete a következő:

\\\(E\_k \= \\frac\{1\}\{2\}mv^2\\\)

ahol \\\(m\\\) a test tömege (kilogrammban), és \\\(v\\\) a test sebessége (méter per szekundumban). A kinetikus energia mértékegysége a joule (J).

Gyakorló Feladatok a Kinetikus Energiához

1. Egy 2 kg tömegű test 5 m/s sebességgel mozog. Mekkora a kinetikus energiája?
2. Egy autó kinetikus energiája 100 kJ, tömege 1000 kg. Mekkora a sebessége?
3. Hasonlítsa össze egy 1 kg-os, 10 m/s sebességgel mozgó test és egy 2 kg-os, 5 m/s sebességgel mozgó test kinetikus energiáját.

Megoldások a Kinetikus Energia Feladataihoz

1. \\\(E\_k \= \\frac\{1\}\{2\} \\times 2 \\text\{ kg\} \\times \(5 \\text\{ m/s\}\)^2 \= 1 \\text\{ kg\} \\times 25 \\text\{ m\}^2/\\text\{s\}^2 \= 25 \\text\{ J\}\\\)
2. \\\(100 \\times 10^3 \\text\{ J\} \= \\frac\{1\}\{2\} \\times 1000 \\text\{ kg\} \\times v^2\\\). Ebből \\\(v^2 \= \\frac\{2 \\times 100 \\times 10^3\}\{1000\} \= 200 \\text\{ m\}^2/\\text\{s\}^2\\\), tehát \\\(v \= \\sqrt\{200\} \\approx 14\.14 \\text\{ m/s\}\\\).
3. Az első test kinetikus energiája: \\\(E\_\{k1\} \= \\frac\{1\}\{2\} \\times 1 \\text\{ kg\} \\times \(10 \\text\{ m/s\}\)^2 \= 50 \\text\{ J\}\\\). A második test kinetikus energiája: \\\(E\_\{k2\} \= \\frac\{1\}\{2\} \\times 2 \\text\{ kg\} \\times \(5 \\text\{ m/s\}\)^2 \= 25 \\text\{ J\}\\\). Tehát az első test kinetikus energiája kétszer akkora.

Potenciális Energia: A Helyzetből Származó Energia

A potenciális energia (\\\(E\_p\\\)) egy test helyzetéből vagy konfigurációjából adódó energia. A leggyakrabban tárgyalt potenciális energiafajták a gravitációs potenciális energia és a rugalmas potenciális energia.

Gravitációs Potenciális Energia

A gravitációs potenciális energia egy test magasságától függ a gravitációs térben. A Föld felszínéhez közeli gravitációs potenciális energia képlete:

\\\(E\_p \= mgh\\\)

ahol \\\(m\\\) a test tömege, \\\(g\\\) a gravitációs gyorsulás (kb. \\\(9\.81 \\text\{ m/s\}^2\\\) a Földön), és \\\(h\\\) a test magassága egy referencia szinthez képest.

Gyakorló Feladatok a Gravitációs Potenciális Energiához

1. Egy 0.5 kg tömegű labdát 10 m magasra emelünk. Mekkora a gravitációs potenciális energiája a talajhoz képest?
2. Egy 50 kg tömegű személy egy 30 m magas épület tetején áll. Mekkora a gravitációs potenciális energiája a talajszinthez viszonyítva?
3. Egy 2 kg-os könyv egy polcon van, amely a talajtól 1.5 m magasan található. Mekkora a könyv gravitációs potenciális energiája?

Megoldások a Gravitációs Potenciális Energia Feladataihoz

1. \\\(E\_p \= 0\.5 \\text\{ kg\} \\times 9\.81 \\text\{ m/s\}^2 \\times 10 \\text\{ m\} \= 49\.05 \\text\{ J\}\\\)

2. \\\(E\_p \= 50 \\text\{ kg\} \\times 9\.81 \\text\{ m/s\}^2 \\times 30 \\text\{ m\} \= 14715 \\text\{ J\}\\\)
3. \\\(E\_p \= 2 \\text\{ kg\} \\times 9\.81 \\text\{ m/s\}^2 \\times 1\.5 \\text\{ m\} \= 29\.43 \\text\{ J\}\\\)

Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmasan deformált testben tárolt energia, például egy megnyújtott vagy összenyomott rugóban. A rugalmas potenciális energia képlete:

\\\(E\_p \= \\frac\{1\}\{2\}kx^2\\\)

ahol \\\(k\\\) a rugóállandó (N/m), és \\\(x\\\) a rugó egyensúlyi helyzetétől való elmozdulása (méterben).

Gyakorló Feladatok a Rugalmas Potenciális Energiához

1. Egy rugó rugóállandója 100 N/m. Mekkora a rugalmas potenciális energia, ha a rugót 0.1 m-rel megnyújtjuk?
2. Egy rugalmas katapultot 0.2 m-rel húzunk hátra. A rugóállandó 500 N/m. Mekkora a tárolt rugalmas potenciális energia?
3. Egy rugóban 10 J rugalmas potenciális energia tárolódik, amikor 0.5 m-rel van összenyomva. Mekkora a rugóállandó?

Megoldások a Rugalmas Potenciális Energia Feladataihoz

1. \\\(E\_p \= \\frac\{1\}\{2\} \\times 100 \\text\{ N/m\} \\times \(0\.1 \\text\{ m\}\)^2 \= 0\.5 \\times 100 \\times 0\.01 \\text\{ J\} \= 0\.5 \\text\{ J\}\\\)
2. \\\(E\_p \= \\frac\{1\}\{2\} \\times 500 \\text\{ N/m\} \\times \(0\.2 \\text\{ m\}\)^2 \= 0\.5 \\times 500 \\times 0\.04 \\text\{ J\} \= 10 \\text\{ J\}\\\)
3. \\\(10 \\text\{ J\} \= \\frac\{1\}\{2\} \\times k \\times \(0\.5 \\text\{ m\}\)^2\\\). Ebből \\\(k \= \\frac\{2 \\times 10\}\{0\.25\} \= 80 \\text\{ N/m\}\\\).

A Munka és az Energia Kapcsolata: A Munkatétel

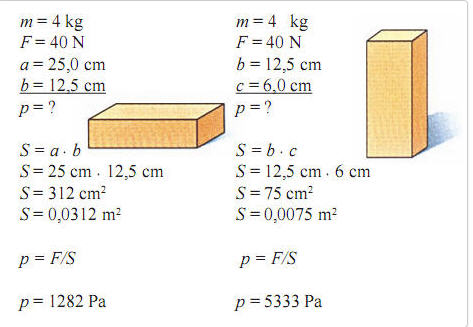
A munka (\\\(W\\\)) az az energia, amely egy testre ható erő hatására megváltozik. Ha egy erő elmozdít egy testet, akkor munkát végez az erő. A munka képlete:

\\\(W \= Fd\\cos\(\\theta\)\\\)

ahol \\\(F\\\) az erő nagysága, \\\(d\\\) az elmozdulás nagysága, és \\\(\\theta\\\) az erő és az elmozdulás közötti szög.

A Munkatétel: A Munka és a Kinetikus Energia Változása

A munkatétel kimondja, hogy egy testre ható összes munka egyenlő a test kinetikus energiájának megváltozásával:

\\\(W\_\{összes\} \= \\Delta E\_k \= E\_\{k,végső\} \- E\_\{k,kezdeti\}\\\)

Gyakorló Feladatok a Munkatételhez

1. Egy 10 kg tömegű test kezdetben nyugalomban van. Egy 20 N-os vízszintes erő hat rá 5 méteren keresztül. Mekkora a test végső kinetikus energiája és sebessége?
2. Egy autó sebessége 20 m/s-ról 30 m/s-ra nő, miközben 500 m-en keresztül gyorsul. A tömege 1500 kg. Mekkora a motor által végzett munka?
3. Egy labdát függőlegesen felfelé dobunk. Kezdeti kinetikus energiája 100 J. A legmagasabb ponton a kinetikus energiája 0 J. Mekkora munkát végzett a gravitációs erő?

Megoldások a Munkatétel Feladataihoz

1. A végzett munka: \\\(W \= Fd \= 20 \\text\{ N\} \\times 5 \\text\{ m\} \= 100 \\text\{ J\}\\\). A munkatétel szerint \\\(\\Delta E\_k \= W\\\), így \\\(E\_\{k,végső\} \- 0 \= 100 \\text\{ J\}\\\), tehát \\\(E\_\{k,végső\} \= 100 \\text\{ J\}\\\). A végső sebességből: \\\(100 \\text\{ J\} \= \\frac\{1\}\{2\} \\times 10 \\text\{ kg\} \\times v^2\\\), \\\(v^2 \= 20 \\text\{ m\}^2/\\text\{s\}^2\\\), \\\(v \= \\sqrt\{20\} \\approx 4\.47 \\text\{ m/s\}\\\).
2. A kezdeti kinetikus energia: \\\(E\_\{k,kezdeti\} \= \\frac\{1\}\{2\} \\times 1500 \\text\{ kg\} \\times \(20 \\text\{ m/s\}\)^2 \= 300000 \\text\{ J\} \= 300 \\text\{ kJ\}\\\). A végső kinetikus energia: \\\(E\_\{k,végső\} \= \\frac\{1\}\{2\} \\times 1500 \\text\{ kg\} \\times \(30 \\text\{ m/s\}\)^2 \= 675000 \\text\{ J\} \= 675 \\text\{ kJ\}\\\). A végzett munka: \\\(W \= \\Delta E\_k \= 675 \\text\{ kJ\} \- 300 \\text\{ kJ\} \= 375 \\text\{ kJ\}\\\).
3. A gravitációs erő lefelé hat, az elmozdulás felfelé. A végzett munka \\\(W \= \\Delta E\_k \= 0 \- 100 \\text\{ J\} \= \-100 \\text\{ J\}\\\). A negatív előjel azt jelzi, hogy a gravitációs erő a mozgás ellenében végez munkát.

Az Energiamegmaradás Törvénye

Az energiamegmaradás törvénye az egyik legalapvetőbb fizikai törvény. Kimondja, hogy egy zárt rendszer teljes energiája állandó marad, bár az energia egyik formájából a másikba alakulhat át. Mechanikai rendszerekben ez azt jelenti, hogy a kinetikus és potenciális energia összege állandó, ha csak konzervatív erők (mint a gravitáció és a rugóerő) végeznek munkát.

\\\(E\_\{mechanikai\} \= E\_k \+ E\_p \= állandó\\\)

Feladatok az Energiamegmaradás Törvényéhez

1. Egy 1 kg tömegű labdát 20 m magasról elejtünk. Mekkora a sebessége, amikor eléri a talajt (elhanyagolva a légellenállást)?
2. Egy 0.2 kg tömegű golyót egy rugó segítségével lőnek ki vízszintesen. A rugóállandó 500 N/m, és a rugót 0.1 m-rel nyomták össze. Mekkora a golyó kilövési sebessége?
3. Egy hullámvasút kocsija egy 40 m magas pontról indul ki nyugalomban. Mekkora a sebessége egy 10 m magas ponton (elhanyagolva a súrlódást)?

Megoldások az Energiamegmaradás Törvénye Feladataihoz

1. A kezdeti mechanikai energia (a legmagasabb ponton): \\\(E\_\{kezdeti\} \= E\_\{k,kezdeti\} \+ E\_\{p,kezdeti\} \= 0 \+ mgh \= 1 \\text\{ kg\} \\times 9\.81 \\text\{ m/s\}^2 \\times 20 \\text\{ m\} \= 196\.2 \\text\{ J\}\\\). A talajon a potenciális energia nulla