Magneses Terersseg Mer Mszer

A mágneses térerősség mérése: Elmélet, eszközök és gyakorlati alkalmazások

A mágneses térerősség mérése alapvető fontosságú számos tudományos, ipari és technológiai területen. Legyen szó akár egy egyszerű mágnes erejének meghatározásáról, akár komplex elektromágneses rendszerek optimalizálásáról, a pontos mérés elengedhetetlen. Ebben az átfogó útmutatóban részletesen bemutatjuk a mágneses térerősség fogalmát, a mérésére szolgáló különböző eszközöket, a mérési elveket és a gyakorlati alkalmazásokat, hogy Ön teljes képet kapjon erről a fontos területről.

Mi a mágneses térerősség? Alapfogalmak és definíciók

A mágneses térerősség egy fizikai mennyiség, amely leírja a mágneses tér intenzitását egy adott pontban. Két fő mennyiség használatos a mágneses tér jellemzésére: a mágneses indukció (\\mathbf\{B\}), amelyet gyakran mágneses fluxussűrűségnek is neveznek, és a mágneses térerősség (\\mathbf\{H\}). Bár a köznapi nyelvben gyakran szinonimaként használják őket, fizikailag különböző fogalmakat takarnak.

A mágneses indukció (\\mathbf\{B\})

A mágneses indukció (\\mathbf\{B\}) azt a erőt írja le, amelyet egy mozgó töltött részecske tapasztal a mágneses térben. Vektor mennyiség, iránya megadja a mágneses erő irányát, nagysága pedig arányos a töltés sebességével és a mágneses tér erősségével. A mágneses indukció mértékegysége a Tesla (T) a Nemzetközi Mértékegységrendszerben (SI). Egy Tesla egyenlő egy Newton per Amperméterrel (N/(A·m)). Egy régebbi, de még ma is használt mértékegység a Gauss (G), ahol 1 T = 10 000 G.

A mágneses térerősség (\\mathbf\{H\})

A mágneses térerősség (\\mathbf\{H\}) egy másik vektor mennyiség, amely a mágneses tér forrásaitól, azaz az áramoktól és a mágneses anyagoktól függ. Kapcsolatban áll a mágneses indukcióval a közeg permeabilitásán (\\mu) keresztül: \\mathbf\{B\} \= \\mu \\mathbf\{H\}. Vákuumban ez az összefüggés \\mathbf\{B\} \= \\mu\_0 \\mathbf\{H\}, ahol \\mu\_0 a vákuum permeabilitása (4\\pi \\times 10^\{\-7\} \\, \\text\{H/m\}). A mágneses térerősség mértékegysége az Amper per méter (A/m) az SI rendszerben.

Miért fontos a kettő megkülönböztetése?

A mágneses indukció (\\mathbf\{B\}) a mágneses tér fizikai hatásait írja le, míg a mágneses térerősség (\\mathbf\{H\}) a tér létrehozásában szerepet játszó áramokhoz és mágneses anyagokhoz kapcsolódik közvetlenebbül. Anyag jelenlétében a permeabilitás (\\mu) befolyásolja a kettő közötti kapcsolatot, ezért fontos a megkülönböztetés, különösen mágneses anyagokkal foglalkozó alkalmazásokban.

A mágneses térerősség mérőműszerei: Áttekintés és működési elvek

Számos különböző elven működő mérőműszer létezik a mágneses térerősség mérésére. A leggyakrabban használtak közé tartoznak a Hall-effektus alapú mérők, a fluxgate magnetométerek, a SQUID magnetométerek és az NMR magnetométerek. Mindegyik típusnak megvannak a maga előnyei és hátrányai a mérési tartomány, az érzékenység, a pontosság és a költség tekintetében.

Hall-effektus alapú mérők (Gaussmérők, Tesla mérők)

A Hall-effektus egy olyan jelenség, amely akkor lép fel, ha egy áramot vezető anyagot mágneses térbe helyeznek, amely merőleges az áram irányára. Ekkor a töltött részecskékre a Lorentz-erő hat, ami töltésszétválasztáshoz és egy, az áramra és a mágneses térre is merőleges feszültség (a Hall-feszültség) kialakulásához vezet. A Hall-feszültség nagysága arányos a mágneses indukció (\\mathbf\{B\}) erősségével.

Működési elv

A Hall-effektus alapú mérők egy vékony félvezető anyagból készült Hall-elemet tartalmaznak. Amikor a Hall-elemet egy mágneses térbe helyezik, és áramot vezetnek rajta keresztül, a keletkező Hall-feszültséget mérik. Ez a feszültség kalibrálható úgy, hogy közvetlenül megadja a mágneses indukció értékét Gaussban vagy Teslában. Ezek a mérők általában robusztusak, könnyen használhatók és széles mérési tartományban alkalmazhatók.

Alkalmazási területek

A Hall-effektus alapú mérőket széles körben használják az iparban, a kutatásban és a minőségellenőrzésben. Néhány tipikus alkalmazás:

• Állandó mágnesek erősségének mérése
• Elektromágnesek térerősségének mérése
• Mágneses szeparátorok és más mágneses berendezések ellenőrzése
• Geomágneses mérések (kevésbé érzékeny változatokkal)

Fluxgate magnetométerek

A fluxgate magnetométerek a magas permeabilitású mag telítésének elvén működnek. Egy ferromágneses magot egy váltakozó árammal meghajtott tekercs vesz körül. A váltakozó áram a magot periodikusan telítésbe viszi. Külső mágneses tér jelenlétében a telítési ciklus aszimmetrikussá válik, ami egy második tekercsben egy második harmonikus frekvenciájú feszültséget indukál. Ennek a feszültségnek az amplitúdója arányos a külső mágneses tér erősségével.

Működési elv

A fluxgate magnetométerek nagy érzékenységükről ismertek, különösen alacsony frekvenciájú és statikus mágneses terek mérésére. Gyakran használják őket a geomágneses tér mérésére, űrkutatási alkalmazásokban és a gyenge mágneses anomáliák detektálására.

Alkalmazási területek

• Geomágneses kutatások és navigáció
• Űrkutatás (bolygóközi mágneses terek mérése)
• Geofizikai feltárás (ásványkutatás, régészet)
• Biztonságtechnika (fémérzékelők)

SQUID magnetométerek (Superconducting Quantum Interference Device)

A SQUID magnetométerek rendkívül érzékeny eszközök, amelyek a szupravezetés kvantummechanikai jelenségeit használják ki a mágneses fluxus nagyon pontos mérésére. Egy SQUID egy vagy több Josephson-átmenetet tartalmaz egy szupravezető hurokban. A mágneses fluxus változása a hurokban kvantált áramok és feszültségek változását eredményezi, amelyek rendkívül kis mágneses térerősségek mérésére is alkalmasak.

Működési elv

A SQUID magnetométerek a legérzékenyebb ismert mágneses tér mérők. Működésükhöz rendkívül alacsony hőmérsékletre (néhány Kelvin) van szükség, hogy a szupravezető állapotot fenntartsák. Alkalmazásaik közé tartozik az orvosi képalkotás (magnetoenkefalográfia, magnetokardiográfia), a geológia, az anyagtudomány és az alapvető fizikai kutatások.

Alkalmazási területek

• Orvosi képalkotás (MEG, MCG)
• Geológia és geofizika (nagyon gyenge mágneses anomáliák mérése)
• Anyagtudomány (mágneses tulajdonságok vizsgálata)
• Alapvető fizikai kutatások

NMR magnetométerek (Nuclear Magnetic Resonance)

Az NMR magnetométerek az atommagok mágneses momentumának a külső mágneses térrel való kölcsönhatásán alapulnak. Bizonyos atommagok (pl. a hidrogénmag, azaz a proton) spinje mágneses momentummal rendelkezik. Külső mágneses térben ezek a momentumok a tér irányába rendeződnek. Ha egy rádiófrekvenciás impulzust alkalmazunk, amely rezonanciában van a magok precessziós frekvenciájával (Larmor-frekvencia), akkor a magok gerjesztődnek. A gerjesztett magok ezután egy gyenge rádiófrekvenciás jelet bocsátanak ki, amelynek frekvenciája arányos a külső mágneses tér erősségével.

Működési elv

Az NMR magnetométerek nagy pontossággal képesek mérni a mágneses indukciót. Gyakran használják őket a geomágneses tér abszolút mérésére és laboratóriumi standardként a mágneses tér kalibrálására.

Alkalmazási területek

• Geomágneses mérések (abszolút érték mérése)
• Laboratóriumi standardok és kalibrálás
• Orvosi képalkotás (MRI – Magnetic Resonance Imaging, amely az NMR elvén működik, bár nem közvetlenül a térerősséget méri kívülről)

A mágneses térerősség mérésének gyakorlata: Fontos szempontok

A pontos mágneses térerősség méréséhez figyelembe kell venni néhány fontos szempontot, mint például a mérőműszer megfelelő kiválasztása, a kalibrálás, a környezeti hatások és a mérési eljárás.

A megfelelő mérőműszer kiválasztása

A mérési feladathoz leginkább megfelelő mérőműszer kiválasztása kulcsfontosságú. Figyelembe kell venni a mérendő mágneses tér várható erősségét, a szükséges pontosságot, a mérési környezetet (pl. hőmérséklet, jelen lévő egyéb elektromágneses mezők) és a költségvetést.

Kalibrálás

A mérőműszerek rendszeres kalibrálása elengedhetetlen a pontos mérések biztosításához. A kalibrálás során a mérőműszer által mutatott értékeket összehasonlítják egy ismert, pontos standarddal, és szükség esetén korrekciós tényezőket alkalmaznak.

Környezeti hatások

A mérést befolyásolhatják a környezetben jelen lévő egyéb mágneses és elektromos mezők, valamint a hőmérséklet. Fontos, hogy a mérést olyan helyen végezzük, ahol a zavaró hatások minimalizálhatók. Bizonyos esetekben árnyékolást kell alkalmazni a külső mágneses terek kizárására.

Mérési eljárás

A mérési eljárást a mérőműszer típusa és a mérendő mágneses tér jellege határozza meg. Pontszerű mérés esetén a szenzort a kívánt mérési pontba kell helyezni. Térbeli eloszlás mérése esetén a szenzort a vizsgált tér különböző pontjain kell végigmozgatni, vagy több szenzort kell egyszerre használni.

A mágneses térerősség mérésének alkalmazásai

A mágneses térerősség mérésének rendkívül széleskörű alkalmazásai vannak a különböző tudományterületeken és az iparban.

Tudományos kutatás

A fizikában, a geofizikában, az asztrofizikában és a biológiai tudományokban a mágneses térerősség mérése alapvető fontosságú. Például a plazmafizikai kísérletekben a mágneses tér konfigurációjának és erősségének ismerete elengedhetetlen a plazma bezárásához. A geofizikában a Föld mágneses terének vizsgálata segít megérteni a bolygó belső szerkezetét és a geomágneses jelenségeket. Az asztrofizikában a csillagok és galaxisok mágneses tereinek mérése fontos információkat nyújt ezeknek az objektumoknak a keletkezéséről és fejlődéséről. A biológiában pedig az élőlények által keltett gyenge mágneses mezők vizsgálata (biomagnetizmus) új kutatási irányokat nyit meg.

Ipari alkalmazások

Az iparban a mágneses térerősség mérése a minőségellenőrzés, a folyamatirányítás és a biztonságtechnika területén játszik fontos szerepet. Például a mágneses anyagok gyártásánál a végtermék mágneses tulajdonságainak ellenőrzése elengedhetetlen. Az elektromos gépek (motorok, generátorok, transzformátorok) tervezésénél és gyártásánál a mágneses tér eloszlásának pontos ismerete kulcsfontosságú a hatékony működéshez. A roncsolásmentes anyagvizsgálatban a mágneses részecskés vizsgálat a felületi és a felület közeli hibák kimutatására szolgál, amelynek során a mágneses tér deformációit detektálják. A biztonságtechnikában a fémérzékelők a mágneses tér megzavarásának elvén működnek.

Orvosi alkalmazások

Az orvosi diagnosztikában a mágneses tér mérésén alapuló eljárások egyre fontosabbá válnak. A magnetoenkefalográfia (MEG) az agyi aktivitás által keltett rendkívül gyenge mágneses mezőket méri, és lehetővé teszi az agyi funkciók nem invazív vizsgálatát. A magnetokardiográfia (MCG) a szív elektromos aktivitása által keltett mágneses mezőket rögzíti. A mágneses rezonancia képalkotás (MRI)

Magneses Indukcio Fogalma

A mágneses indukció fogalma és részletes magyarázata

Ebben a kimerítő cikkben mélyrehatóan feltárjuk a mágneses indukció lenyűgöző jelenségét. Célunk, hogy egy átfogó képet nyújtsunk erről az alapvető fizikai fogalomról, amely az elektromágnesesség megértésének sarokköve. Részletesen elemezzük a definícióját, a hozzá kapcsolódó alapelveket, a matematikai leírását, a mérési egységeit, valamint a gyakorlati alkalmazásait a mindennapi életben és a modern technológiában. Kísérletekkel és szemléletes példákkal illusztráljuk a jelenséget, hogy az olvasó számára a lehető legvilágosabb és legérthetőbb legyen.

Mi a mágneses indukció? A definíció részletes elemzése

A mágneses indukció, más néven mágneses fluxussűrűség vagy röviden B-mező, egy vektormennyiség, amely leírja a mágneses tér erősségét és irányát egy adott pontban. Képzeljünk el egy olyan teret, ahol mágneses hatások érvényesülnek. A mágneses indukció megmutatja, hogy egy mozgó töltésre vagy egy árammal átjárt vezetőre mekkora erő hat ezen a ponton, és milyen irányban. Ez a fogalom elengedhetetlen az elektromágneses jelenségek, mint például az elektromos motorok, generátorok és transzformátorok működésének megértéséhez.

A mágneses indukció mint vektormennyiség

Fontos hangsúlyozni, hogy a mágneses indukció egy vektormennyiség, ami azt jelenti, hogy nemcsak nagysága van, hanem iránya is. Az irányát hagyományosan úgy definiáljuk, hogy az a方向ba mutat, amerre egy képzeletbeli északi pólusú tesztmágnes elmozdulna a tér adott pontjában. A nagysága pedig azt adja meg, hogy milyen erős a mágneses hatás. Ezt a kettős tulajdonságot vektorokkal ábrázoljuk, ahol a vektor hossza a nagyságot, a nyíl pedig az irányt jelöli.

A mágneses indukció és a mágneses tér közötti kapcsolat

A mágneses tér egy olyan térrész, ahol mágneses erők hatnak. A mágneses indukció ennek a térnek egy lokális jellemzője. Minden pontban a mágneses térben definiálhatunk egy mágneses indukció vektort. Különböző források hozhatnak létre mágneses teret, például állandó mágnesek vagy elektromos árammal átjárt vezetők. Az általuk létrehozott mágneses tér minden pontjában létezik egy jól definiált mágneses indukció.

A mágneses indukció matematikai leírása és képletei

A mágneses indukciót pontosan leírhatjuk matematikai egyenletek segítségével. Ezek az egyenletek nemcsak a jelenség kvantitatív megértéséhez elengedhetetlenek, hanem lehetővé teszik a mágneses mezőkkel kapcsolatos számításokat és előrejelzéseket is.

A Lorentz-erő és a mágneses indukció kapcsolata

A mágneses indukció egyik legfontosabb definíciója a Lorentz-erőn keresztül történik. Egy q töltésű részecskére, amely \\mathbf\{v\} sebességgel mozog egy \\mathbf\{B\} mágneses indukciójú térben, a mágneses erő (\\mathbf\{F\}\_m) a következőképpen adható meg:

\\mathbf\{F\}\_m \= q \(\\mathbf\{v\} \\times \\mathbf\{B\}\)

Ez az egyenlet megmutatja, hogy a mágneses erő merőleges mind a részecske sebességére, mind a mágneses indukció vektorára. A kereszttermék (\\times) eredményezi a erő irányát, amelyet a jobbkéz-szabállyal határozhatunk meg. Ha a töltés pozitív, akkor a mágneses erő iránya a jobb kezünk hüvelykujjának irányába mutat, ha az ujjaink a sebesség irányába görbülnek, és a tenyerünk a mágneses indukció irányába néz.

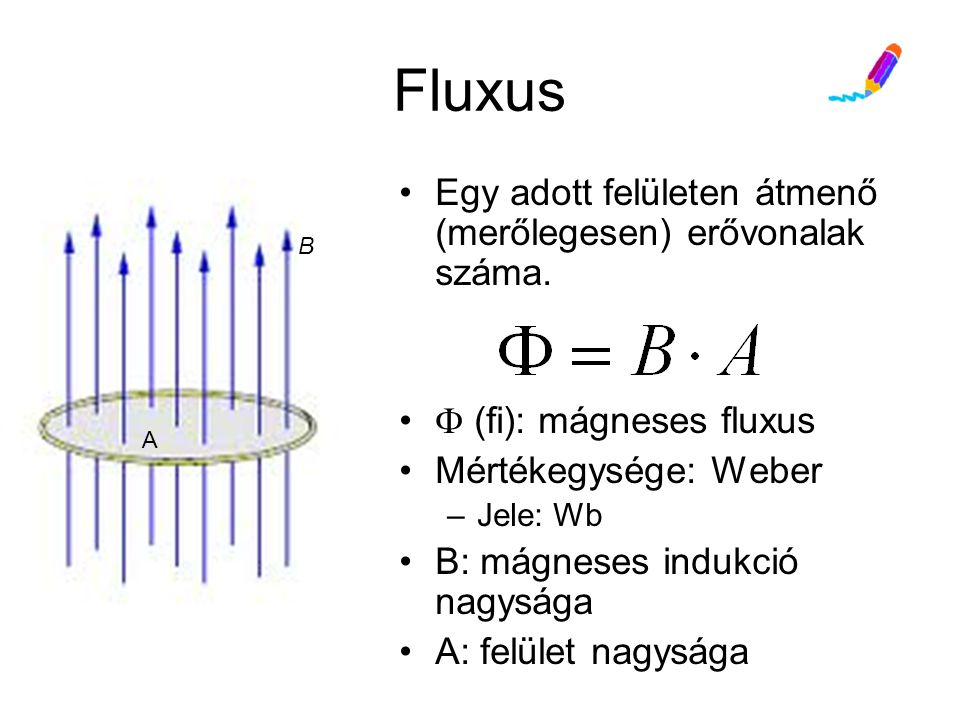
A mágneses fluxus és a mágneses indukció kapcsolata

Egy másik fontos fogalom a mágneses fluxus (\\Phi\_B), amely megadja, hogy mennyi a mágneses mező “áramlik át” egy adott felületen. A mágneses fluxus a mágneses indukció és a felület vektoros szorzatának integrálja:

\\Phi\_B \= \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}

Ha a mágneses mező homogén a felületen, és a felület normálvektora párhuzamos a mágneses indukcióval, akkor az egyenlet egyszerűsödik:

\\Phi\_B \= B A \\cos \\theta

ahol B a mágneses indukció nagysága, A a felület területe, és \\theta a mágneses indukció és a felület normálvektora közötti szög.

A mágneses indukció mértékegységei

A mágneses indukció SI-mértékegysége a Tesla (T). Egy Tesla egyenlő egy Newton per Amper-méter (N/Am). Ez a definíció a Lorentz-erő képletéből származik:

1 \\, \\text\{T\} \= 1 \\, \\frac\{\\text\{N\}\}\{\\text\{A\} \\cdot \\text\{m\}\}

Egy másik, régebbi mértékegység a Gauss (G). A Tesla és a Gauss közötti kapcsolat a következő:

1 \\, \\text\{T\} \= 10^4 \\, \\text\{G\}

A gyakorlatban mindkét egységet használják, de a tudományos közösségben a Tesla az elfogadottabb SI-egység.

Példák a tipikus mágneses indukció értékekre

• A Föld mágneses tere a felszín közelében: kb. 10^\{\-4\} T (0.5 Gauss körül).
• Egy hűtőmágnes: kb. 10^\{\-2\} T (100 Gauss körül).

• Egy erős ipari mágnes: néhány Tesla.
• Egy orvosi MRI készülék mágneses tere: tipikusan 1.5-3 Tesla, de léteznek erősebb rendszerek is.

A mágneses indukció forrásai

A mágneses indukció, azaz a mágneses tér különböző forrásokból származhat. A két fő forrás az állandó mágnesek és az elektromos áram.

Állandó mágnesek

Az állandó mágnesek olyan anyagok, amelyek atomi szinten rendezett mágneses dipólusokkal rendelkeznek. Ezek a dipólusok eredetileg az elektronok spinjéből és keringéséből származnak. Bizonyos anyagokban, mint például a ferromágneses anyagokban (pl. vas, nikkel, kobalt), ezek a dipólusok spontán módon egy irányba rendeződhetnek, még külső mágneses tér hiányában is, létrehozva egy makroszkopikus mágneses teret. Az állandó mágneseknek van egy északi és egy déli pólusuk, és a mágneses tér vonalai az északi pólustól indulnak ki, és a déli pólusban végződnek a mágnesen kívül, míg a mágnesen belül a déli pólustól az északi pólus felé haladnak.

Elektromos áram

Egy másik, rendkívül fontos forrása a mágneses indukciónak az elektromos áram. Amikor elektromos töltések mozognak, mágneses teret hoznak létre maguk körül. Ezt a jelenséget írja le az Ampère-törvény. Egy egyenes, hosszú vezető körül, amelyben I áram folyik, a mágneses indukció (\\mathbf\{B\}) körkörös vonalak mentén helyezkedik el a vezető körül, és a nagysága a következőképpen adható meg:

B \= \\frac\{\\mu\_0 I\}\{2 \\pi r\}

ahol \\mu\_0 a vákuum permeabilitása (4\\pi \\times 10^\{\-7\} \\, \\text\{T\} \\cdot \\text\{m/A\}), I az áram erőssége, és r a vezetőtől mért távolság. A mágneses tér irányát itt is a jobbkéz-szabállyal határozhatjuk meg: ha a hüvelykujjunk az áram irányába mutat, akkor a begörbülő ujjaink a mágneses tér vonalainak irányát jelzik.

Elektromágnesek

Az elektromos áram mágneses hatását kihasználva hozhatunk létre elektromágneseket. Egy tekercsbe (szolenoidba) vezetett elektromos áram sokkal erősebb és irányíthatóbb mágneses teret generál, mint egy egyenes vezető. A szolenoid belsejében a mágneses tér közel homogén, és a nagysága arányos a tekercs menetszámával, az áram erősségével és fordítottan arányos a tekercs hosszával (hosszú szolenoid esetén). Az elektromágnesek kulcsfontosságúak számos technológiai alkalmazásban, a reléktől kezdve az MRI-berendezésekig.

A mágneses indukció fontos törvényei

Számos alapvető fizikai törvény írja le a mágneses indukció viselkedését és kapcsolatát más fizikai mennyiségekkel.

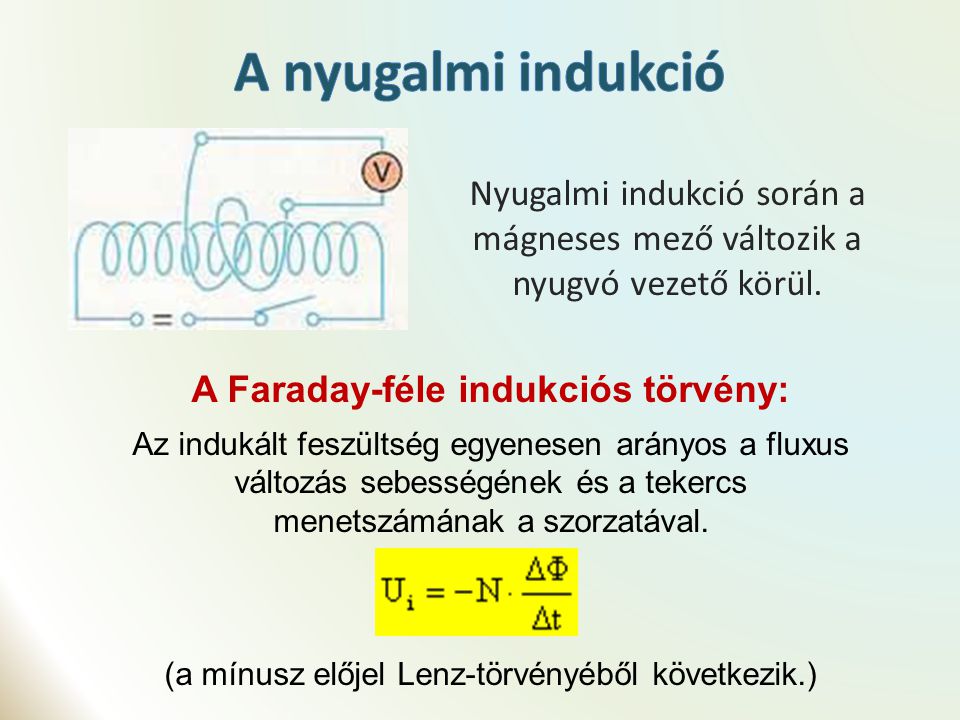
Faraday indukciós törvénye

A Faraday indukciós törvénye az egyik legfontosabb törvény az elektromágnesességben. Kimondja, hogy ha egy zárt vezetőhurokban megváltozik a mágneses fluxus, akkor a hurokban elektromotoros erő (EMF) indukálódik. Az indukált EMF nagysága egyenlő a mágneses fluxus időbeli változásának sebességével:

\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}

A negatív előjel a Lenz-törvényt tükrözi, amely kimondja, hogy az indukált áram (és az általa létrehozott mágneses tér) olyan irányú, hogy akadályozza a fluxus változását, amely létrehozta.

Lenz törvénye

Ahogy említettük, a Lenz törvénye kiegészíti Faraday törvényét azáltal, hogy megadja az indukált áram irányát. Ha egy mágnes közeledik egy tekercshez, az indukált áram olyan mágneses teret hoz létre, amely taszítja a mágnest. Ha a mágnes távolodik, az indukált áram olyan mágneses teret hoz létre, amely vonzza a mágnest. Ez az “ellenállás” a fluxus változásával szemben az energia megmaradásának elvéből következik.

Gauss törvénye a mágnesességre

A Gauss törvénye a mágnesességre kimondja, hogy nincsenek mágneses monopólusok, azaz nincsenek olyan “mágneses töltések”, amelyekből a mágneses térvonalak kiindulnának vagy amelyekben végződnének. Matematikailag ezt úgy fejezzük ki, hogy egy zárt felületen átmenő mágneses fluxus mindig nulla:

\\oint \\mathbf\{B\} \\cdot d\\mathbf\{A\} \= 0

Ez azt jelenti, hogy a mágneses térvonalak mindig zárt hurkokat alkotnak.

Ampère törvénye (kibővítve Maxwell korrekciójával)

Az Ampère törvénye eredetileg az elektromos áram és az általa létrehozott mágneses tér közötti kapcsolatot írta le:

\\oint \\mathbf\{B\} \\cdot d\\mathbf\{l\} \= \\mu\_0 I\_\{enc\}

ahol az integrál egy zárt görbe mentén történik, és I\_\{enc\} a görbe által körülvett áram. Maxwell kiegészítette ezt a törvényt a eltolási áram fogalmával, hogy figyelembe vegye a változó elektromos mezők mágneses hatását is. A Maxwell-Ampère törvény kibővített formája:

\\oint \\mathbf\{B\} \\cdot d\\mathbf\{l\} \= \\mu\_0 \\left\(I\_\{enc\} \+ \\epsilon\_0 \\frac\{d\\Phi\_E\}\{dt\}\\right\)

ahol \\epsilon\_0 a vákuum permittivitása, és \\frac\{d\\Phi\_E\}\{dt\} az elektromos fluxus időbeli változásának sebessége.

Kísérletek a mágneses indukció bemutatására

A mágneses indukció jelensége látványos kísérletekkel demonstrálható, amelyek segítenek a fogalom intuitív megértésében.

Mágnes mozgatása tekercsben

Egy egyszerű, de szemléletes kísérlet, ha egy állandó mágnest mozgatunk egy tekercs belsejében vagy annak közelében. Ha a mágnest a tekercsbe toljuk, a tekercsben feszültség indukálódik, és ha egy zárt áramkör részét képezi a tekercs, akkor áram is folyik. Amikor a mágnes áll, nincs indukált feszültség vagy áram. Ha a mágnest kihúzzuk a tekercsből, ismét feszültség indukálódik, de az ellenkező polaritással, ami fordított irányú áramot eredményez.

Két tekercs kísérlete

Egy másik klasszikus kísérlet két egymás közelében elhelyezett tekercset használ. Ha az egyik tekercsben (primer tekercs) változtatjuk az áramot (például be- vagy kikapcsoljuk, vagy a nagyságát változtatjuk), akkor a változó mágneses fluxus a másik tekercsen (szekunder tekercs) keresztül is áthalad, és abban feszültséget indukál. Ez az elv áll a transzformátorok működésének hátterében.

A mágneses indukció alkalmazásai

A mágneses indukció elvén számos nélkülözhetetlen technológiai eszköz és berendezés működik.

Elektromos generátorok

Az elektromos generátorok mechanikai energiát alakítanak át elektromos energiává a mágneses indukció segítségével. Egy vezetőhurkot (vagy tekercset) egy mágneses térben forgatnak, vagy egy mágneses teret forgatnak egy álló vezetőhurok körül. Mindkét esetben a vezetőhurkon áthaladó mágneses fluxus változik, ami elektromotoros erőt (feszültséget) indukál a hurokban. Ez az

Magneses Indukcio Felhasznalasa

A mágneses indukció felhasználása: Átfogó útmutató

A mágneses indukció az elektromágnesesség egyik alapvető jelensége, amely nélkül a modern technológia elképzelhetetlen lenne. Lényege, hogy egy változó mágneses tér elektromos mezőt hoz létre, ami elektromos áramot indukálhat egy vezetőben. Ez az elv képezi számos nélkülözhetetlen eszköz és technológia működésének alapját, a mindennapi háztartási gépektől a komplex ipari berendezésekig és a csúcstechnológiás orvosi eljárásokig. Ebben a részletes útmutatóban feltárjuk a mágneses indukció sokrétű felhasználási területeit, bemutatva annak fontosságát és a mögötte rejlő tudományos alapelveket.

A mágneses indukció alapjai: Faraday törvénye

A mágneses indukció jelenségét Michael Faraday fedezte fel az 1830-as években. Faraday törvénye kvantitatívan írja le az indukált elektromotoros erő (EMF) nagyságát egy zárt áramkörben. A törvény kimondja, hogy az indukált EMF egyenesen arányos a zárt áramkörön áthaladó mágneses fluxus időbeli változásának sebességével. Matematikailag ezt a következőképpen fejezhetjük ki:

\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}

Ahol \\mathcal\{E\} az indukált elektromotoros erő (voltokban), \\Phi\_B a mágneses fluxus (weberben), és t az idő (másodpercekben). A negatív előjel (Lenz törvénye) azt jelzi, hogy az indukált áram olyan irányú, hogy mágneses terével akadályozza a fluxus változását, amely létrehozta őt. Ez az alapelv kulcsfontosságú a mágneses indukció számos alkalmazásának megértéséhez.

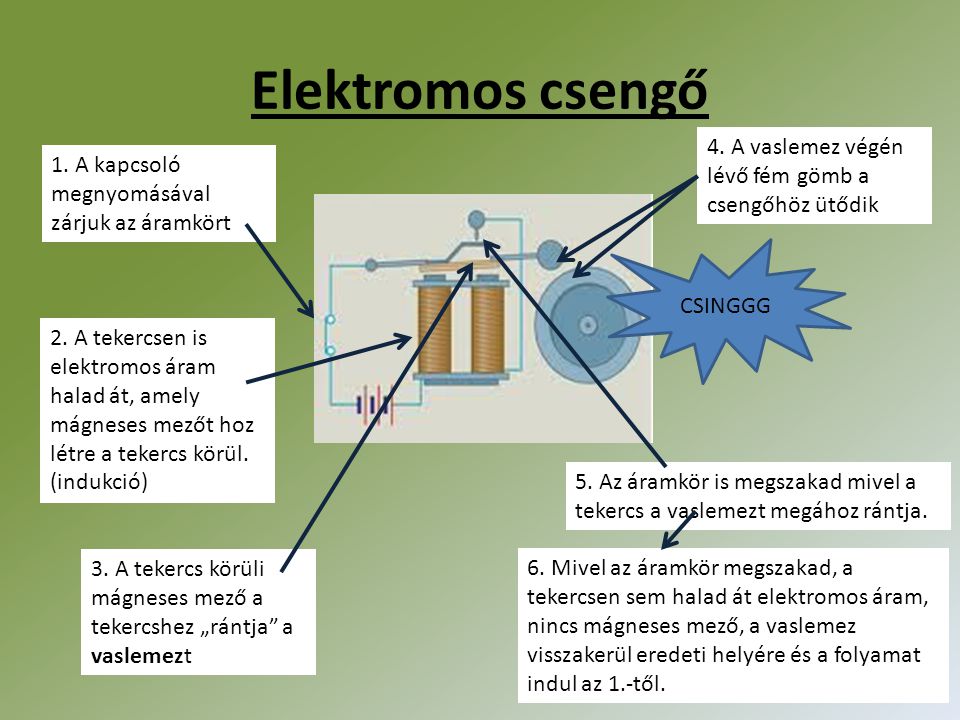
A mágneses fluxus fogalma

A mágneses fluxus (\\Phi\_B) a mágneses térnek egy adott felületen áthaladó mértéke. Homogén mágneses tér esetén, amely merőleges egy A területű felületre, a mágneses fluxus a mágneses indukció (B) és a terület szorzata: \\Phi\_B \= B \\cdot A. Ha a mágneses tér nem merőleges a felületre, akkor a fluxus a \\Phi\_B \= B \\cdot A \\cdot \\cos\(\\theta\) képlettel számítható ki, ahol \\theta a mágneses tér és a felület normálvektora közötti szög.

Lenz törvényének jelentősége

Lenz törvénye, amely a negatív előjelben nyilvánul meg Faraday törvényében, alapvető a mágneses indukció irányának meghatározásában. Ez a törvény biztosítja az energiamegmaradás elvét az elektromágneses indukció folyamatában. Az indukált áram mindig olyan mágneses teret hoz létre, amely ellentétes az eredeti mágneses fluxus változásával. Ez a visszacsatolási mechanizmus elengedhetetlen számos elektromos eszköz stabil és hatékony működéséhez.

A mágneses indukció gyakorlati felhasználási területei

A mágneses indukció elvén működő technológiák áthatják mindennapi életünket és a modern ipar számos területét. A következőkben részletesen bemutatjuk a legfontosabb alkalmazásokat.

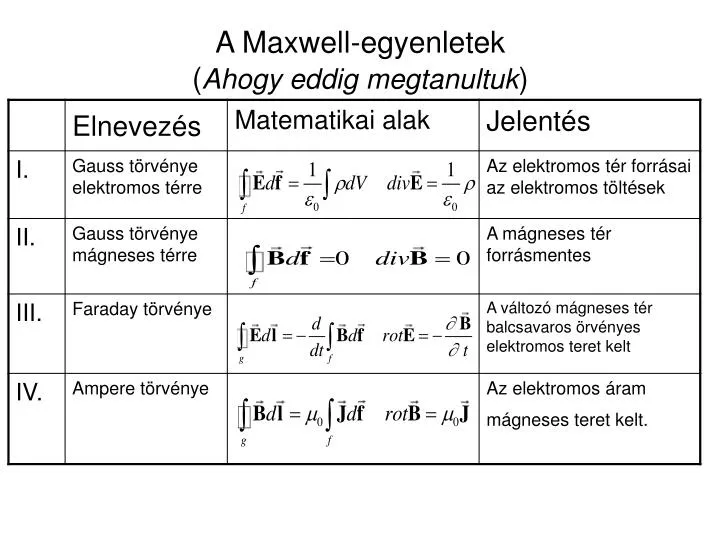
Elektromos transzformátorok

Az elektromos transzformátorok a mágneses indukció egyik legfontosabb és legelterjedtebb alkalmazását képviselik. Ezek az eszközök lehetővé teszik a váltakozó feszültség szintjének megváltoztatását anélkül, hogy a frekvencia megváltozna. Egy ideális transzformátor két tekercsből áll, amelyek egy közös vasmagra vannak feltekercselve. Az egyik tekercsre (primer tekercs) váltakozó feszültséget kapcsolunk, ami változó mágneses fluxust hoz létre a vasmagban. Ez a változó fluxus a másik tekercsben (szekunder tekercs) elektromotoros erőt indukál. A primer és szekunder tekercsek menetszámainak aránya határozza meg a feszültség transzformációjának mértékét:

\\frac\{V\_p\}\{V\_s\} \= \\frac\{N\_p\}\{N\_s\}

Ahol V\_p a primer feszültség, V\_s a szekunder feszültség, N\_p a primer tekercs menetszáma, és N\_s a szekunder tekercs menetszáma.

A transzformátorok szerepe az energiaelosztásban

A transzformátorok kulcsfontosságúak az elektromos energia hatékony elosztásában. A távvezetékeken nagy feszültséggel továbbítják az áramot, hogy csökkentsék az ellenállásból adódó veszteségeket (P \= I^2R). A generátoroknál termelt alacsonyabb feszültséget transzformátorokkal növelik fel a távvezetékekhez szükséges magas feszültségre. A fogyasztási helyeken aztán újabb transzformátorok csökkentik a feszültséget a biztonságos és használható szintre (pl. 230 V háztartási feszültség).

Különféle típusú transzformátorok

Számos különböző típusú transzformátor létezik, amelyek speciális alkalmazásokhoz készülnek. Ide tartoznak például a hálózati transzformátorok, a leválasztó transzformátorok, az impulzus transzformátorok és az audio transzformátorok. Mindegyik típus a mágneses indukció elvén működik, de kialakításuk és paramétereik az adott feladathoz vannak optimalizálva.

Elektromos generátorok

Az elektromos generátorok a mágneses indukció elvét használják fel mechanikai energia elektromos energiává alakítására. Egy egyszerű generátor egy mágneses térben forgó vezető hurokból áll. Amikor a hurok forog, a rajta áthaladó mágneses fluxus változik, ami elektromotoros erőt indukál a hurokban. Ezt az indukált EMF-et aztán elektromos áramként lehet kinyerni.

A generátorok működési elve

A generátorok működésének alapja Faraday indukciós törvénye. A mechanikai energia (pl. vízturbina, gőzturbina, szélkerék által biztosított forgatás) a vezető hurkot vagy tekercset a mágneses térben mozgatja. Ez a mozgás megváltoztatja a mágneses fluxust a tekercsen keresztül, indukálva ezzel elektromos feszültséget. A feszültség polaritása a hurok mágneses térhez viszonyított mozgásának irányától függ (Lenz törvénye).

Különféle típusú generátorok

Számos különböző típusú elektromos generátor létezik, amelyeket a felhasznált energiaforrás és a generált áram típusa szerint csoportosíthatunk. Ide tartoznak az AC (váltakozó áramú) generátorok (alternátorok) és a DC (egyenáramú) generátorok (dinamók). A nagy erőművekben használt turbinák hatalmas alternátorokat hajtanak meg, míg a kisebb, hordozható generátorok belső égésű motorokat használnak a forgatáshoz.

Elektromotorok

Az elektromotorok a mágneses indukció egy másik fontos alkalmazását képviselik, bár itt az elv fordított a generátorokhoz képest. Az elektromotorok elektromos energiát alakítanak át mechanikai energiává. Működésük azon alapul, hogy egy árammal átfolyó vezetőre mágneses tér erőhatást fejt ki (Lorentz-erő). A motorok gyakran tartalmaznak tekercseket, amelyek mágneses teret hoznak létre, és kölcsönhatásba lépnek egy állandó mágnes vagy egy másik elektromágnes terével, ami forgómozgást eredményez.

Az elektromotorok működési elve

Ha egy árammal átfolyó vezető egy mágneses térben helyezkedik el, akkor a vezetőre erő hat. Ennek az erőnek az iránya a Fleming-féle bal kéz szabályával határozható meg. Az elektromotorokban tekercseket használnak, hogy növeljék a létrehozott forgatónyomatékot. A kommutátor (DC motorokban) vagy a váltakozó áramú táplálás (AC motorokban) biztosítja, hogy a forgórészre ható erő mindig a forgás irányába mutasson.

Az elektromotorok széleskörű alkalmazása

Az elektromotorokat a legkülönbözőbb területeken használják, a háztartási gépektől (pl. mosógépek, hűtőszekrények, ventilátorok) az ipari berendezésekig (pl. szerszámgépek, futószalagok) és a közlekedésig (pl. elektromos autók, vonatok). Az elektromotorok hatékonyak, megbízhatóak és sokféle méretben és teljesítményben elérhetőek.

Indukciós főzőlapok

Az indukciós főzőlapok a mágneses indukció egy modern és hatékony háztartási alkalmazását jelentik. Ezek a főzőlapok nem a főzőlap felületét melegítik fel közvetlenül, hanem egy elektromágneses mezőt hoznak létre, amely a megfelelő edény aljában indukál áramot (örvényáramokat). Ez az indukált áram az edény anyagának ellenállása miatt hőt termel, így magát az edényt és annak tartalmát melegíti fel.

Az indukciós főzés előnyei

Az indukciós főzés számos előnnyel jár a hagyományos főzési módszerekkel szemben. Gyorsabb a felfűtési idő, mivel a hő közvetlenül az edényben keletkezik. Energiahatékonyabb, mert kevesebb hő vész kárba. Biztonságosabb, mivel a főzőlap felülete csak az edénytől melegszik fel, és gyorsan lehűl, ha az edényt eltávolítják. Emellett precízebb hőmérséklet-szabályozást tesz lehetővé.

Az indukciós főzéshez használt edények

Az indukciós főzéshez olyan edények szükségesek, amelyeknek az alja ferromágneses anyagból (pl. vas, acél) készül. Ez azért fontos, mert a mágneses térnek képesnek kell lennie áramot indukálni az edény aljában. Az alumínium vagy réz edények önmagukban nem működnek indukciós főzőlapon, hacsak nincs ferromágneses réteg az aljukon.

Vezeték nélküli töltés

A vezeték nélküli töltési technológiák szintén a mágneses indukció elvén alapulnak. Két tekercset használnak: egyet az adóban (pl. töltőpadban) és egyet a vevőben (pl. okostelefonban). Amikor az adó tekercsén váltakozó áram folyik át, változó mágneses teret hoz létre. Ha a vevő tekercs a mágneses tér közelébe kerül, ebben a tekercsben elektromos áram indukálódik, amely a készülék akkumulátorának töltésére használható.

A vezeték nélküli töltés működése

A legelterjedtebb vezeték nélküli töltési szabvány a Qi szabvány, amely induktív csatolást használ. Az adó tekercs egy rezonáns áramkör része, amely egy bizonyos frekvencián működik. Amikor a vevő tekercs a közelbe kerül, a két áramkör rezonánsan csatolódik, lehetővé téve az energia hatékony átvitelét. A töltési sebesség és hatékonyság függ a tekercsek közötti távolságtól és a rendszer kialakításától.

A vezeték nélküli töltés alkalmazásai

A vezeték nélküli töltést egyre szélesebb körben alkalmazzák okostelefonok, okosórák, vezeték nélküli fülhallgatók és más hordozható elektronikai eszközök töltésére. Emellett kutatások folynak nagyobb teljesítményű vezeték nélküli töltési rendszerek kifejlesztésére elektromos járművekhez is.

Mágneses rezonancia képalkotás (MRI)

A mágneses rezonancia képalkotás (MRI) egy orvosi képalkotó eljárás, amely erős mágneses teret és rádióhullámokat használ a test részletes képeinek létrehozásához. Bár az MRI nem közvetlenül a mágneses indukció klasszikus elvén működik, az elektromágneses indukció elengedhetetlen szerepet játszik a jelek detektálásában.

Az MRI működési elve

Az MRI során a pácienst egy erős mágneses térbe helyezik, amely a testben lévő vízmolekulákban található protonok (hidrogénatomok magjai) spinjét rendezi. Ezután rádiófrekvenciás impulzusokat bocsátanak ki, amelyek átmenetileg megzavarják ezt az alignmentet. Amikor a protonok visszatérnek eredeti állapotukba, rádióhullámokat bocsátanak ki. Ezeket a jeleket érzékeny tekercsekkel (amelyek a mágneses indukció elvén működnek) detektálják, és számítógépes algoritmusok segítségével részletes képeket alkotnak a test belső szerkezetéről.

Az MRI jelentősége az orvosi diagnosztikában

Az MRI rendkívül értékes diagnosztikai eszköz, amely kiváló lágyrész-kontrasztot biztosít, így különösen alkalmas agy, gerincvelő, ízületek és más lágy szövetek vizsgálatára. Nem használ ionizáló sugárzást (mint a röntgen vagy a CT), ezért biztonságosabb eljárásnak tekinthető bizonyos esetekben.

Egyéb alkalmazások

A fentieken túl a mágneses indukció számos más területen is fontos szerepet játszik:

• Indukciós érzékelők: Fémek jelenlétének érzékelésére használják, például érintésmentes