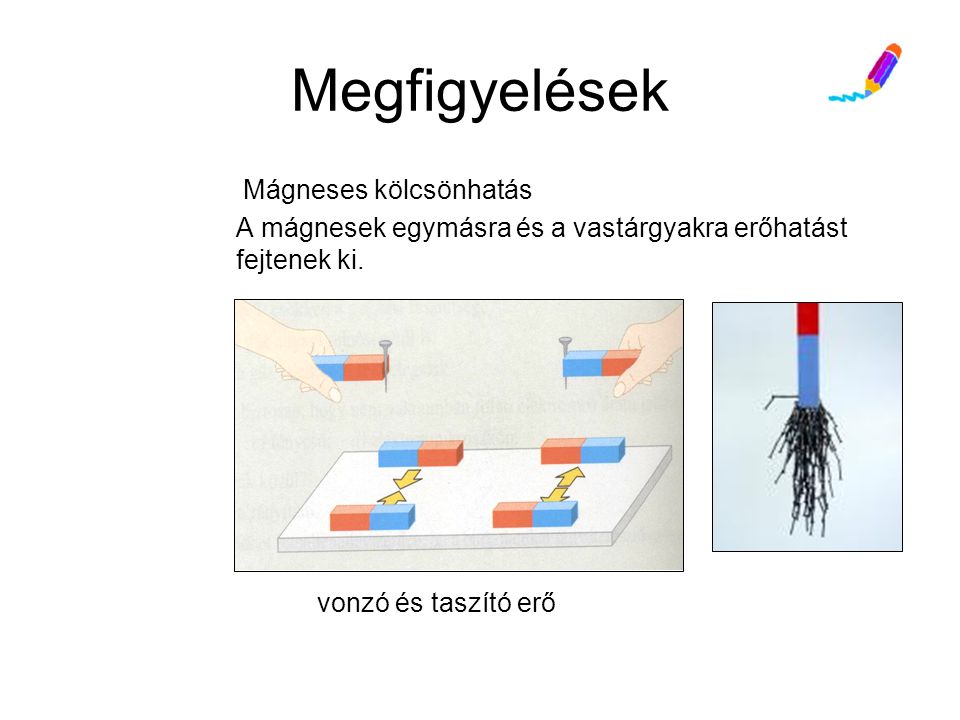
Magneses Megosztas
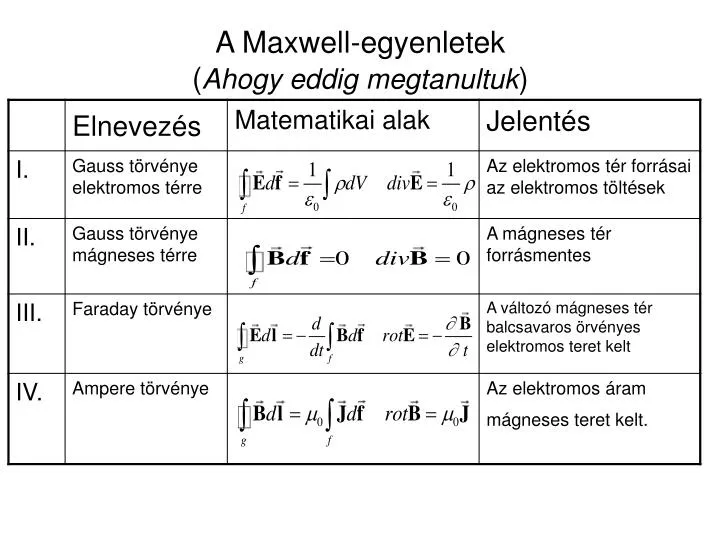
A Mágneses Megosztás Átfogó Tanulmánya: Elmélet, Alkalmazások és Jövőbeli Lehetőségek
A mágneses megosztás egy lenyűgöző jelenség, amely a fizika alapvető erői közé tartozó mágnesesség elvén alapszik. Ez a fogalom sokkal többet foglal magában, mint csupán két mágnes vonzását vagy taszítását. A modern tudomány és technológia számos területén kulcsszerepet játszik, az energiaátviteltől kezdve az adatmentésen át a legkülönfélébb szenzorok működéséig. Ebben a részletes elemzésben mélyrehatóan feltárjuk a mágneses megosztás elméleti alapjait, a gyakorlati alkalmazásainak széles spektrumát, a legújabb kutatási eredményeket és a jövőbeli potenciálját.
A Mágnesesség Alapjai és a Mágneses Megosztás Elve
A mágnesesség egy olyan fizikai jelenség, amelyet a mozgó elektromos töltések hoznak létre. Az atomok elektronjainak mozgása és a spinjük is mágneses momentumot eredményez. Az anyagok mágneses tulajdonságai attól függenek, hogy ezek a mikroszkopikus mágneses momentumok hogyan rendeződnek. A mágneses megosztás lényegében azt jelenti, hogy egy mágneses tér hatással van egy másik mágneses objektumra, vagy egy mágneses objektum hatással van egy mágneses térre. Ez a kölcsönhatás erőket és nyomatékokat eredményezhet.
A Mágneses Tér és annak Jellemzői
A mágneses tér egy vektormező, amely a mozgó elektromos töltések és a mágneses momentummal rendelkező anyagok körül létezik. A mágneses teret általában a \\mathbf\{B\} szimbólummal jelöljük, és mértékegysége a Tesla (T). A mágneses tér erősségét és irányát a tér minden pontjában definiáljuk. A mágneses tér vonalainak képzeletbeli görbéi segítenek a tér vizualizálásában. Ezek a vonalak a mágnes északi pólusától indulnak és a déli pólusánál érnek véget, a mágnes belsejében pedig zárt hurkokat alkotnak. A mágneses tér erőssége arányos a mágneses térvonalak sűrűségével.
A Biot-Savart Törvény

A Biot-Savart törvény egy alapvető fizikai törvény, amely leírja, hogy egy állandó elektromos áram hogyan hoz létre mágneses teret. A törvény szerint egy I áramot vezető d\\mathbf\{l\} hosszúságú kis vezetőszegmens által egy \\mathbf\{r\} távolságra lévő pontban létrehozott d\\mathbf\{B\} mágneses tér a következőképpen számítható ki:
\\mathbf\{dB\} \= \\frac\{\\mu\_0\}\{4\\pi\} \\frac\{I d\\mathbf\{l\} \\times \\mathbf\{\\hat\{r\}\}\}\{r^2\}
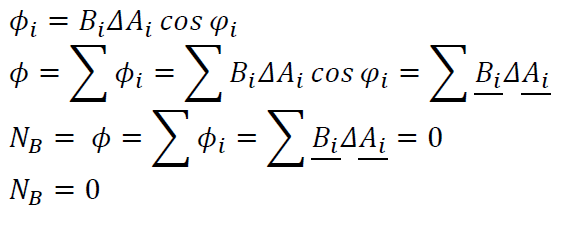
ahol \\mu\_0 a vákuum permeabilitása, és \\mathbf\{\\hat\{r\}\} az egységvektor a vezetőszegmenstől a megfigyelési pontig.
Az Ampère-féle Törvény
Az Ampère-féle törvény egy másik fontos összefüggés a mágnesesség területén, amely a mágneses tér és az áram közötti kapcsolatot írja le. Integrális formájában a törvény kimondja, hogy a mágneses tér vonalintegrálja egy zárt görbe mentén arányos a görbe által körülvett teljes árammal:
\\oint \\mathbf\{B\} \\cdot d\\mathbf\{l\} \= \\mu\_0 I\_\{enc\}
ahol I\_\{enc\} a zárt görbe által körülvett teljes áram.
A Mágneses Erő
Egy mozgó töltésre mágneses tér hatására erő hat. Ezt az erőt Lorentz-erőnek nevezzük, amelynek mágneses komponense a következőképpen adható meg:
\\mathbf\{F\}\_B \= q \(\\mathbf\{v\} \\times \\mathbf\{B\}\)
ahol q a töltés nagysága, \\mathbf\{v\} a töltés sebessége, és \\mathbf\{B\} a mágneses tér. Ez az erő mindig merőleges a töltés sebességére és a mágneses térre is, ezért nem végez munkát a töltésen, csupán megváltoztatja annak mozgásának irányát.
Erő áramvezetőre mágneses térben
Ha egy I áramot vezető vezető d\\mathbf\{l\} hosszúságú szegmense mágneses térben van, akkor erre a szegmensre ható mágneses erő:
d\\mathbf\{F\} \= I d\\mathbf\{l\} \\times \\mathbf\{B\}
Egy véges hosszúságú vezetőre ható teljes erő a fenti kifejezés integrálásával kapható meg a vezető mentén.
Erő két áramvezető között
Két párhuzamos, áramot vezető vezető egymásra mágneses erőt fejt ki. Ha az áramok azonos irányúak, az erők vonzóak, ha ellentétes irányúak, akkor taszítóak. Két hosszú, párhuzamos, d távolságra lévő vezető között, amelyeken I\_1 és I\_2 áram folyik, az egységnyi hosszra jutó erő:
\\frac\{F\}\{L\} \= \\frac\{\\mu\_0 I\_1 I\_2\}\{2\\pi d\}

Mágneses Momentum
A mágneses momentum egy olyan vektor mennyiség, amely egy objektum mágneses erősségét és irányát jellemzi. Egy áramhurok mágneses momentuma a hurok által bezárt terület és az áram szorzatával arányos, és iránya a jobbkéz-szabály szerint adódik:
\\mathbf\{\\mu\} \= I \\mathbf\{A\}
ahol I az áram a hurokban, és \\mathbf\{A\} a hurok által bezárt területvektor (irányát a jobbkéz-szabály adja meg).
Nyomaték mágneses térben lévő mágneses momentumra
Egy \\mathbf\{\\mu\} mágneses momentummal rendelkező objektumra, amely egy \\mathbf\{B\} mágneses térben található, ható nyomaték:
\\mathbf\{\\tau\} \= \\mathbf\{\\mu\} \\times \\mathbf\{B\}
Ez a nyomaték arra törekszik, hogy a mágneses momentumot a mágneses tér irányába forgassa.
A Mágneses Megosztás Alkalmazásai a Technikában
A mágneses megosztás elvén alapuló technológiák rendkívül széles körben elterjedtek a modern világban. Az alábbiakban néhány fontosabb alkalmazást részletezünk.
Elektromágneses Indukció és Energiaátvitel
Az elektromágneses indukció jelensége, amelyet Faraday fedezett fel, alapvető fontosságú az elektromos energia termelésében és átvitelében. Ha egy mágneses tér változik egy vezető hurok környezetében, vagy ha egy vezető hurok mozog egy mágneses térben, akkor a hurokban elektromotoros erő (EMF) indukálódik. Ez az elv áll a transzformátorok és a generátorok működésének hátterében.
Transzformátorok
A transzformátorok olyan eszközök, amelyek elektromágneses indukció segítségével képesek váltakozó feszültséget egyik áramkörből egy másikba átalakítani anélkül, hogy a két áramkör között közvetlen elektromos kapcsolat lenne. Egy tipikus transzformátor két tekercsből (primer és szekunder) áll, amelyek egy közös vasmagra vannak feltekercselve. A primer tekercsben folyó váltakozó áram változó mágneses teret hoz létre a vasmagban, amely indukálja a feszültséget a szekunder tekercsben. A feszültségek aránya a tekercsek menetszámának arányával egyenlő:
\\frac\{V\_p\}\{V\_s\} \= \\frac\{N\_p\}\{N\_s\}
ahol V\_p a primer feszültség, V\_s a szekunder feszültség, N\_p a primer tekercs menetszáma, és N\_s a szekunder tekercs menetszáma.
Generátorok
Az elektromos generátorok mechanikai energiát alakítanak át elektromos energiává az elektromágneses indukció elvén. A legegyszerűbb generátor egy mágneses térben forgó vezető hurkot tartalmaz. A hurok mozgása a mágneses téren keresztül változó mágneses fluxust eredményez a hurokban, ami elektromotoros erőt indukál. A modern erőművekben használt nagyméretű generátorok is ezen az elven működnek, ahol a forgómozgást gőz-, víz- vagy szélturbinák biztosítják.
Vezeték Nélküli Energiaátvitel
A mágneses megosztás lehetővé teszi a vezeték nélküli energiaátvitelt is. Két rezonáns tekercs között, amelyek azonos frekvencián rezonálnak, hatékony energiaátvitel valósulhat meg mágneses rezonancia révén. Ezt a technológiát alkalmazzák például okostelefonok vezeték nélküli töltésére és orvosi implantátumok energiaellátására.
Adatrögzítés és Adatvisszaolvasás
A mágneses megosztás kulcsszerepet játszik az adatok rögzítésében és visszaolvasásában is, különösen a hagyományos merevlemezek (HDD) esetében. Az adatok mágneses rétegen lévő apró mágneses domének polaritásának beállításával kerülnek rögzítésre. Az olvasófej, amely egy érzékeny mágneses szenzort tartalmaz, érzékeli ezeknek a doméneknek a mágneses terét, és így képes visszaolvasni a tárolt információt.

Merevlemezek (HDD)
A merevlemezek több forgó lemezből állnak, amelyek mágneses anyaggal vannak bevonva. A rögzítőfej elektromágnes segítségével képes lokálisan megváltoztatni a mágneses réteg polaritását, így bináris adatokat (0 és 1) tárolva. Az olvasófej egy induktív vagy magnetoreszisztív szenzor segítségével érzékeli a mágneses mező változásait a lemez forgása közben, és ezeket a változásokat elektromos jelekké alakítja, amelyek a tárolt adatoknak felelnek meg.
Mágneskártyák
A mágneskártyák, mint például a hitelkártyák és a beléptető kártyák, egy vékony mágneses csíkot tartalmaznak, amelyen az információ mágnesesen van kódolva. Amikor a kártyát egy olvasón keresztülhúzzák, az olvasófej érzékeli a mágneses csík mezőjét, és dekódolja az azon tárolt adatokat.
Szenzorok és Mérőeszközök
A mágneses megosztás elvén működő szenzorok és mérőeszközök rendkívül érzékenyek és sokoldalúak. Számos területen alkalmazzák őket, a navigációtól kezdve az ipari automatizáláson át az orvosi diagnosztikáig.
Hall-effektus Szenzorok
A Hall-effektus jelensége akkor lép fel, ha egy áramot vezető vezetőt egy mágneses térbe helyezünk, amely merőleges az áram irányára. Ekkor a vezetőben az áramra és a mágneses térre is merőleges irányban feszültség keletkezik, amelyet Hall-feszültségnek nevezünk. A Hall-effektus szenzorok ezt az elvet használják mágneses terek mérésére, pozícióérzékelésre és árammérésre.
Magnetoreszisztív Szenzorok
A magnetoreszisztív szenzorok olyan anyagok ellenállásának változását használják ki, amelyek mágneses tér hatására következnek be. Különböző típusai léteznek, mint például az anizotróp magnetoresztencia (AMR), a gigantikus magnetoresztencia (GMR) és a tunnelező magnetoresztencia (TMR). Ezek a szenzorok rendkívül érzékenyek és széles körben alkalmazzák őket például a merevlemezek olvasófejeiben, az autóiparban (sebesség- és pozícióérzékelők), valamint a biológiai és orvosi diagnosztikában.
SQUID-ok (Szupervezető Kvantum Interferencia Eszközök)
A SQUID-ok rendkívül érzékeny magnetométerek, amelyek a szupravezetés kvantummechanikai jelenségeit használják ki a rendkívül gyenge mágneses terek mérésére. Alkalmazzák őket például az orvosi képalkotásban (magnetoenkefalográfia, magnetokardiográfia), a geofizikában és az alapvető fizikai kutatásokban.
Mágneses Levitatáció
A mágneses levitatáció (maglev) egy olyan jelenség, amelyben egy objektumot mágneses erők segítségével lebegtetnek egy másik objektum felett anélkül, hogy fizikai érintkezés lenne közöttük. Ezt a technológiát alkalmazzák például a maglev vonatoknál, ahol a súrlódás csökkentésével nagy sebességek érhetők el.
Maglev Vonatok
A maglev vonatok erős mágneseket használnak mind a vonat, mind a pálya mentén. A vonatot a pálya fölé emelik és előre hajtják a mágneses erők. Mivel nincs fizikai érintkezés a vonat és a pálya között, a súrlódás jelentősen csökken, ami lehetővé teszi a nagyon nagy sebességek elérését és a csendesebb működést.
Orvosi Alkalmazások
A mágneses megosztás számos orvosi alkalmazásban is fontos szerepet játszik.
Mágneses Rezonancia Képalkotás (MRI)
A mágneses rezonancia képalkotás (MRI) egy orvosi képalkotó eljárás, amely erős mágneses teret és rádióhullámokat használ a test belső szerkezetének részletes képeinek létrehozására. Az MRI a testben lévő vízmolekulákban található hidrogénatomok magjainak mágneses tulajdonságait használja ki.
Mágneses Terá
Magneses Indukcio Keplet
A Mágneses Indukció Képlete: Mélyreható Elemzés és Alkalmazások
A Mágneses Indukció Alapjai
A mágneses indukció egy alapvető jelenség az elektromágnesség területén, amely leírja, hogyan hoz létre egy változó mágneses tér elektromos teret. Ez a kölcsönhatás képezi számos modern technológia működésének alapját, a generátoroktól a transzformátorokig. Ahhoz, hogy teljes mértékben megértsük a mágneses indukció képletét, először is tisztáznunk kell a kapcsolódó alapfogalmakat, mint például a mágneses fluxus és Faraday törvénye.
A Mágneses Fluxus Fogalma
A mágneses fluxus (\\Phi\_B) egy adott felületen áthaladó mágneses tér mennyiségének mértéke. Képzeljünk el egy mágneses teret, amelyet mágneses térvonalakkal ábrázolunk. A mágneses fluxus arányos azzal a vonalszámmal, amely egy adott felületet áthalad. Matematikailag a mágneses fluxust a következőképpen definiáljuk:
\\Phi\_B \= \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}
Ahol \\mathbf\{B\} a mágneses indukció vektor (más néven mágneses tér sűrűség), és d\\mathbf\{A\} a felület egy infiniteszimális elemének vektoros területe, amelynek iránya merőleges a felületre. Ha a mágneses tér homogén a felületen, és a mágneses tér vektor párhuzamos a felület normálisával, akkor a képlet egyszerűsödik:
\\Phi\_B \= BA \\cos\{\\theta\}
Ahol B a mágneses tér erőssége, A a felület területe, és \\theta a mágneses tér vektor és a felület normálisának szöge. A mágneses fluxus mértékegysége a Weber (Wb), ahol 1 Wb = 1 Tm$^2$ (Tesla-négyzetméter).
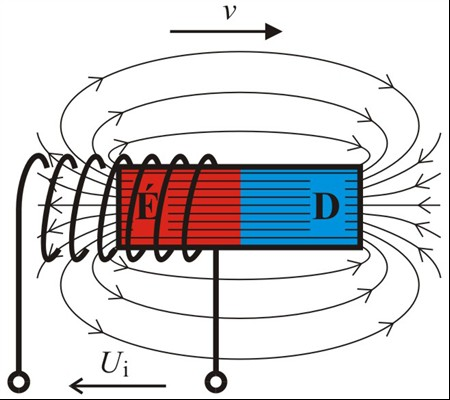
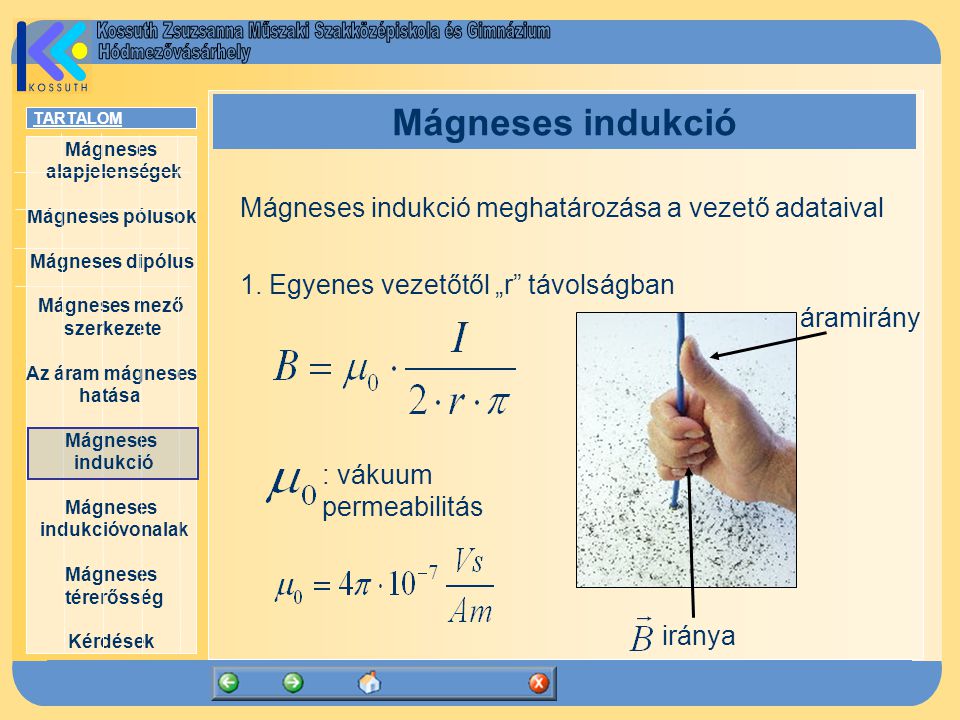
Faraday Indukciós Törvénye
Michael Faraday kísérletei során fedezte fel az elektromágneses indukció alapvető törvényét. Faraday törvénye kimondja, hogy egy zárt áramkörben indukált elektromotoros erő (EMF, \\mathcal\{E\}) egyenlő a mágneses fluxus időbeli változásának negatívjával az áramkörön keresztül:
\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}
Ez a képlet a mágneses indukció képletének központi eleme. A negatív előjel Lenz törvényét tükrözi, amely szerint az indukált áram iránya olyan, hogy mágneses terével akadályozza a fluxus változását, amely létrehozta őt.

Az Indukált Elektromotoros Erő Részletesebben
Az indukált elektromotoros erő (EMF) valójában egy potenciálkülönbség, amely egy vezetőben vagy áramkörben jön létre a változó mágneses fluxus hatására. Ez az EMF képes áramot hajtani, ha az áramkör zárt. A Faraday-féle indukciós törvény kvantitatív kapcsolatot teremt a változó mágneses fluxus és az indukált EMF között.
Lenz Törvényének Szerepe
Mint említettük, a Faraday-féle indukciós törvényben szereplő negatív előjel a Lenz-törvény következménye. Lenz törvénye elengedhetetlen az indukált áram és az indukált mágneses tér irányának meghatározásához. Egyszerűen fogalmazva, az indukált áram olyan irányú, hogy az általa létrehozott mágneses tér ellentétes a fluxus változásával, amely az indukciót okozta. Ez az elv biztosítja az energiamegmaradást az elektromágneses indukciós folyamatokban.
A Mágneses Indukció Képletének Levezetése Mozgó Vezető Esetén
Tekintsünk egy l hosszúságú vezetőt, amely egy homogén \\mathbf\{B\} mágneses térben v sebességgel mozog, úgy hogy a sebességvektor merőleges a mágneses tér vektorra és a vezetőre is. A vezetőben lévő töltött részecskékre (például elektronokra) ható mágneses erő a Lorentz-erő:
\\mathbf\{F\} \= q\(\\mathbf\{v\} \\times \\mathbf\{B\}\)

Ahol q a töltés. Az elektronokra ható erő iránya a jobbkéz-szabály szerint meghatározható. Ennek az erőnek a hatására a töltések a vezető mentén elmozdulnak, ami egy elektromos teret hoz létre a vezetőben. Amikor a mágneses erő által létrehozott elektromos erő egyensúlyba kerül a töltésekre ható mágneses erővel, egy állandó elektromos tér alakul ki.

Az indukált elektromotoros erő a vezető két vége közötti potenciálkülönbség:
\\mathcal\{E\} \= \\int \(\\mathbf\{v\} \\times \\mathbf\{B\}\) \\cdot d\\mathbf\{l\}
Ha \\mathbf\{v\}, \\mathbf\{B\} és d\\mathbf\{l\} páronként merőlegesek egymásra, akkor ez leegyszerűsödik:
\\mathcal\{E\} \= Blv
Ez a képlet azt mutatja, hogy egy mozgó vezetőben indukált EMF arányos a mágneses tér erősségével, a vezető hosszával és a sebességével.
A Mágneses Indukció Képletének Levezetése Változó Mágneses Tér Esetén
Most vizsgáljuk meg azt az esetet, amikor egy rögzített áramkörben változik a mágneses fluxus. Faraday törvénye közvetlenül megadja az indukált EMF-et:
\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}
Ha a mágneses tér időben változik, de a felület állandó, akkor a fluxus időbeli deriváltja a mágneses tér időbeli deriváltjával függ össze:
\\frac\{d\\Phi\_B\}\{dt\} \= \\frac\{d\}\{dt\} \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\} \= \\int \\frac\{\\partial \\mathbf\{B\}\}\{\\partial t\} \\cdot d\\mathbf\{A\}
Így az indukált EMF:
\\mathcal\{E\} \= \-\\int \\frac\{\\partial \\mathbf\{B\}\}\{\\partial t\} \\cdot d\\mathbf\{A\}
Ez a forma a mágneses indukció képletének egy általánosabb megközelítése, amely a változó mágneses tér hatására létrejövő elektromos teret írja le.
A Mágneses Indukció és az Elektromos Tér kapcsolata: Faraday-Maxwell törvény
A Faraday-féle indukciós törvény a Maxwell-egyenletek egyik alapvető formája, amely összekapcsolja a változó mágneses teret az elektromos térrel. Integrális formában a Faraday-Maxwell törvény így szól:
\\oint \\mathbf\{E\} \\cdot d\\mathbf\{l\} \= \-\\frac\{d\}\{dt\} \\iint\_S \\mathbf\{B\} \\cdot d\\mathbf\{A\} \= \-\\frac\{d\\Phi\_B\}\{dt\}
Ahol a bal oldalon az elektromos tér vonalintegrálja egy zárt görbe mentén, a jobb oldalon pedig a mágneses fluxus időbeli változása a görbe által határolt felületen keresztül látható. Ez az egyenlet azt fejezi ki, hogy egy változó mágneses fluxus elektromos teret indukál.
Differenciális formában a Faraday-Maxwell törvény:
\\nabla \\times \\mathbf\{E\} \= \-\\frac\{\\partial \\mathbf\{B\}\}\{\\partial t\}
Ez a forma lokális kapcsolatot ír le a térben az elektromos tér rotációja és a mágneses tér időbeli változása között.
Az Induktivitás Fogalma
Az induktivitás (L) egy áramkör azon tulajdonsága, amely ellenáll az áram változásának önindukció vagy kölcsönös indukció révén. Ha egy áramkörben áram folyik, mágneses fluxust hoz létre, amely arányos az árammal:
\\Phi\_B \= LI
Ahol I az áram. Ha az áram időben változik, a mágneses fluxus is változik, ami Faraday törvénye szerint elektromotoros erőt indukál az áramkörben:
\\mathcal\{E\} \= \-L \\frac\{dI\}\{dt\}
Ez az önindukció jelensége. Az induktivitás mértékegysége a Henry (H).
Kölcsönös Indukció
A kölcsönös indukció akkor lép fel, ha egy áramkörben változó áram egy másik közeli áramkörben is elektromotoros erőt indukál a két áramkör által megosztott mágneses fluxus változása miatt. Ha az 1. áramkörben I\_1 áram folyik, a 2. áramkörben létrejövő mágneses fluxus \\Phi\_\{21\} \= M\_\{21\}I\_1, ahol M\_\{21\} a 2. áramkör 1. áramkörre vonatkozó kölcsönös induktivitása. A 2. áramkörben indukált EMF:
\\mathcal\{E\}\_2 \= \-\\frac\{d\\Phi\_\{21\}\}\{dt\} \= \-M\_\{21\} \\frac\{dI\_1\}\{dt\}
Hasonlóképpen, az 1. áramkörben az áram változása a 2. áramkörben fluxust hoz létre, \\Phi\_\{12\} \= M\_\{12\}I\_2, és az 1. áramkörben indukált EMF:
\\mathcal\{E\}\_1 \= \-\\frac\{d\\Phi\_\{12\}\}\{dt\} \= \-M\_\{12\} \\frac\{dI\_2\}\{dt\}
A Mágneses Indukció Alkalmazásai
A mágneses indukció elve számos technológiai alkalmazás alapját képezi:
Elektromos Generátorok
A generátorok mechanikai energiát alakítanak át elektromos energiává a mágneses indukció segítségével. Egy tekercset vagy vezetőt egy mágneses térben forgatnak, ami a mágneses fluxus változását okozza a tekercsen keresztül, indukálva ezzel egy elektromotoros erőt és áramot.
Transzformátorok
A transzformátorok a kölcsönös indukció elvén működnek. Két vagy több tekercsből állnak, amelyek egy közös mágneses magra vannak feltekercselve. Egyik tekercsben (primer tekercs) változó áramot vezetnek, ami változó mágneses fluxust hoz létre a magban. Ez a változó fluxus elektromotoros erőt indukál a másik tekercsben (szekunder tekercs), lehetővé téve a feszültség és az áram átalakítását.
Indukciós Főzés
Az indukciós főzőlapok változó mágneses teret használnak, hogy áramot indukáljanak a főzőedény aljában. Ez az indukált áram (örvényáram) felmelegíti az edényt, így főzve meg az ételt.
Elektromágneses Fékek
Bizonyos járművekben elektromágneses fékeket használnak, amelyek a mágneses indukció elvén működnek. A mozgó kerekekkel együtt forgó féktárcsába mágneses teret hoznak létre, ami örvényáramokat indukál a tárcsában. Ezek az áramok mágneses teret hoznak létre, amely ellentétes az eredetivel, így fékező hatást eredményez.
Vezeték Nélküli Töltés
A vezeték nélküli töltési technológiák, mint például a mobiltelefonok töltése, szintén a mágneses indukciót használják. Egy adótekercsben váltakozó áramot vezetnek, ami változó mágneses teret hoz létre. Ez a tér elektromos áramot indukál a vevőtekercsben, amely a töltendő eszközben található.
Példák a Mágneses Indukció Képletének Alkalmazására
Példa 1: Mozgó vezető
Egy 0.5 m hosszú vezető 2 T erősségű mágneses térben mozog 10 m/s sebességgel, úgy hogy a sebesség merőleges a mágneses térre és a vezetőre. Számítsuk ki az indukált elektromotoros erőt!
Használjuk a \\mathcal\{E\} \= Blv képletet:
\\mathcal\{E\} \= \(2 \\, \\text\{T\}\) \\times \(0\.5 \\, \\text\{m\}\) \\times \(10 \\, \\text\{m/s\}\) \= 10 \\, \\text\{V\}
Tehát az indukált elektromotoros erő 10 V.
Példa 2: Változó mágneses fluxus
Egy 0.1 m
Magneses Indukcio Fogalma
A mágneses indukció fogalma és részletes magyarázata
Ebben a kimerítő cikkben mélyrehatóan feltárjuk a mágneses indukció lenyűgöző jelenségét. Célunk, hogy egy átfogó képet nyújtsunk erről az alapvető fizikai fogalomról, amely az elektromágnesesség megértésének sarokköve. Részletesen elemezzük a definícióját, a hozzá kapcsolódó alapelveket, a matematikai leírását, a mérési egységeit, valamint a gyakorlati alkalmazásait a mindennapi életben és a modern technológiában. Kísérletekkel és szemléletes példákkal illusztráljuk a jelenséget, hogy az olvasó számára a lehető legvilágosabb és legérthetőbb legyen.
Mi a mágneses indukció? A definíció részletes elemzése
A mágneses indukció, más néven mágneses fluxussűrűség vagy röviden B-mező, egy vektormennyiség, amely leírja a mágneses tér erősségét és irányát egy adott pontban. Képzeljünk el egy olyan teret, ahol mágneses hatások érvényesülnek. A mágneses indukció megmutatja, hogy egy mozgó töltésre vagy egy árammal átjárt vezetőre mekkora erő hat ezen a ponton, és milyen irányban. Ez a fogalom elengedhetetlen az elektromágneses jelenségek, mint például az elektromos motorok, generátorok és transzformátorok működésének megértéséhez.
A mágneses indukció mint vektormennyiség
Fontos hangsúlyozni, hogy a mágneses indukció egy vektormennyiség, ami azt jelenti, hogy nemcsak nagysága van, hanem iránya is. Az irányát hagyományosan úgy definiáljuk, hogy az a方向ba mutat, amerre egy képzeletbeli északi pólusú tesztmágnes elmozdulna a tér adott pontjában. A nagysága pedig azt adja meg, hogy milyen erős a mágneses hatás. Ezt a kettős tulajdonságot vektorokkal ábrázoljuk, ahol a vektor hossza a nagyságot, a nyíl pedig az irányt jelöli.
A mágneses indukció és a mágneses tér közötti kapcsolat
A mágneses tér egy olyan térrész, ahol mágneses erők hatnak. A mágneses indukció ennek a térnek egy lokális jellemzője. Minden pontban a mágneses térben definiálhatunk egy mágneses indukció vektort. Különböző források hozhatnak létre mágneses teret, például állandó mágnesek vagy elektromos árammal átjárt vezetők. Az általuk létrehozott mágneses tér minden pontjában létezik egy jól definiált mágneses indukció.
A mágneses indukció matematikai leírása és képletei
A mágneses indukciót pontosan leírhatjuk matematikai egyenletek segítségével. Ezek az egyenletek nemcsak a jelenség kvantitatív megértéséhez elengedhetetlenek, hanem lehetővé teszik a mágneses mezőkkel kapcsolatos számításokat és előrejelzéseket is.
A Lorentz-erő és a mágneses indukció kapcsolata
A mágneses indukció egyik legfontosabb definíciója a Lorentz-erőn keresztül történik. Egy q töltésű részecskére, amely \\mathbf\{v\} sebességgel mozog egy \\mathbf\{B\} mágneses indukciójú térben, a mágneses erő (\\mathbf\{F\}\_m) a következőképpen adható meg:
\\mathbf\{F\}\_m \= q \(\\mathbf\{v\} \\times \\mathbf\{B\}\)
Ez az egyenlet megmutatja, hogy a mágneses erő merőleges mind a részecske sebességére, mind a mágneses indukció vektorára. A kereszttermék (\\times) eredményezi a erő irányát, amelyet a jobbkéz-szabállyal határozhatunk meg. Ha a töltés pozitív, akkor a mágneses erő iránya a jobb kezünk hüvelykujjának irányába mutat, ha az ujjaink a sebesség irányába görbülnek, és a tenyerünk a mágneses indukció irányába néz.
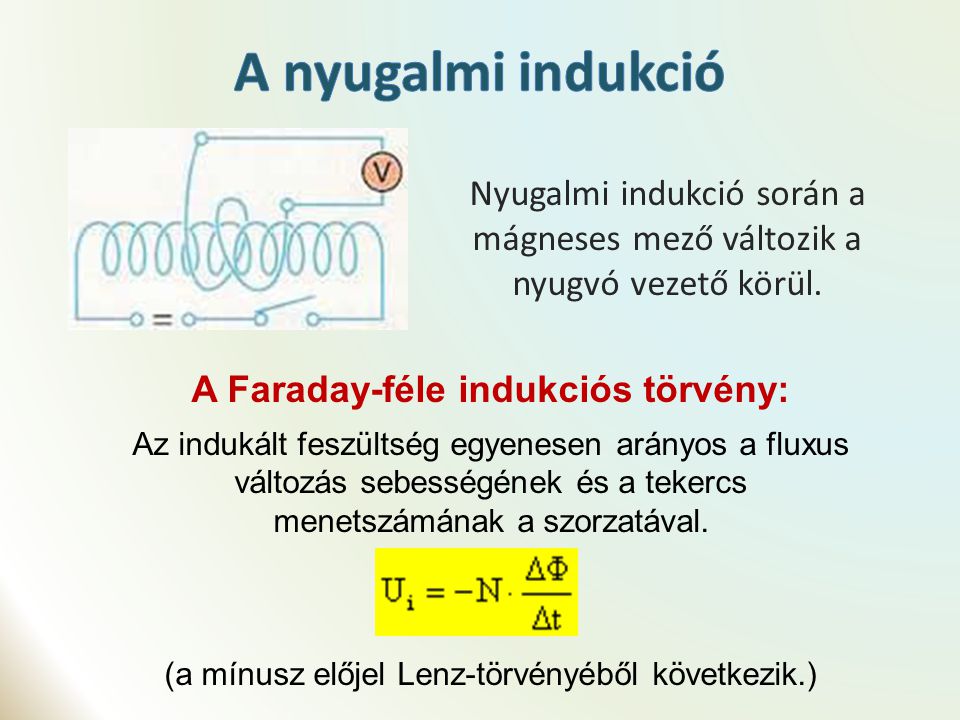
A mágneses fluxus és a mágneses indukció kapcsolata
Egy másik fontos fogalom a mágneses fluxus (\\Phi\_B), amely megadja, hogy mennyi a mágneses mező “áramlik át” egy adott felületen. A mágneses fluxus a mágneses indukció és a felület vektoros szorzatának integrálja:
\\Phi\_B \= \\int \\mathbf\{B\} \\cdot d\\mathbf\{A\}
Ha a mágneses mező homogén a felületen, és a felület normálvektora párhuzamos a mágneses indukcióval, akkor az egyenlet egyszerűsödik:
\\Phi\_B \= B A \\cos \\theta
ahol B a mágneses indukció nagysága, A a felület területe, és \\theta a mágneses indukció és a felület normálvektora közötti szög.
A mágneses indukció mértékegységei
A mágneses indukció SI-mértékegysége a Tesla (T). Egy Tesla egyenlő egy Newton per Amper-méter (N/Am). Ez a definíció a Lorentz-erő képletéből származik:
1 \\, \\text\{T\} \= 1 \\, \\frac\{\\text\{N\}\}\{\\text\{A\} \\cdot \\text\{m\}\}
Egy másik, régebbi mértékegység a Gauss (G). A Tesla és a Gauss közötti kapcsolat a következő:
1 \\, \\text\{T\} \= 10^4 \\, \\text\{G\}
A gyakorlatban mindkét egységet használják, de a tudományos közösségben a Tesla az elfogadottabb SI-egység.
Példák a tipikus mágneses indukció értékekre
- A Föld mágneses tere a felszín közelében: kb. 10^\{\-4\} T (0.5 Gauss körül).
- Egy hűtőmágnes: kb. 10^\{\-2\} T (100 Gauss körül).
- Egy erős ipari mágnes: néhány Tesla.
- Egy orvosi MRI készülék mágneses tere: tipikusan 1.5-3 Tesla, de léteznek erősebb rendszerek is.


A mágneses indukció forrásai
A mágneses indukció, azaz a mágneses tér különböző forrásokból származhat. A két fő forrás az állandó mágnesek és az elektromos áram.
Állandó mágnesek
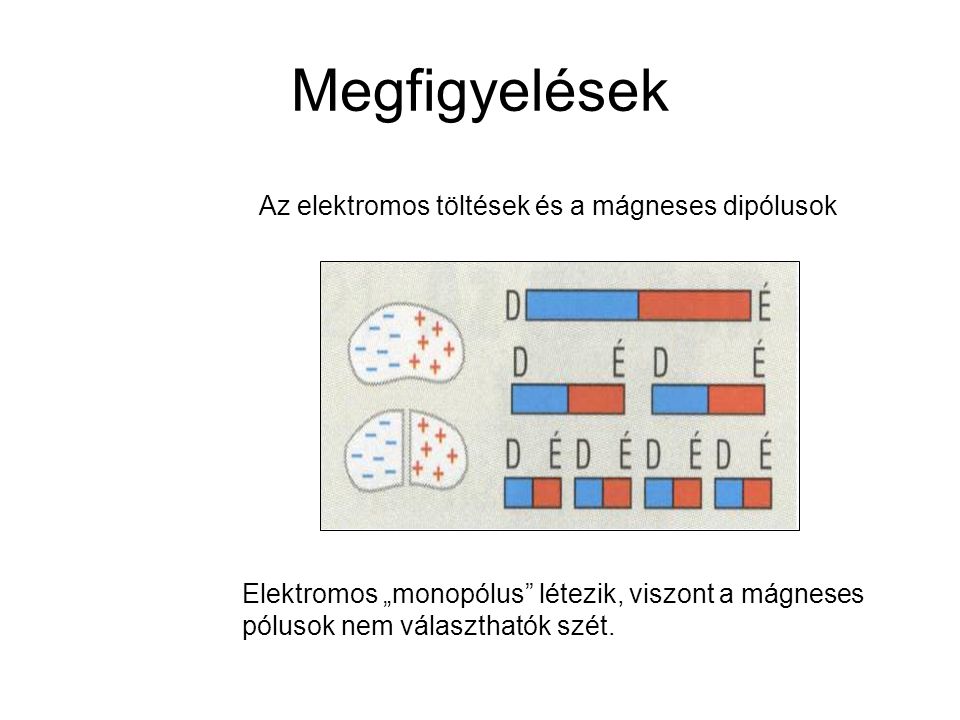
Az állandó mágnesek olyan anyagok, amelyek atomi szinten rendezett mágneses dipólusokkal rendelkeznek. Ezek a dipólusok eredetileg az elektronok spinjéből és keringéséből származnak. Bizonyos anyagokban, mint például a ferromágneses anyagokban (pl. vas, nikkel, kobalt), ezek a dipólusok spontán módon egy irányba rendeződhetnek, még külső mágneses tér hiányában is, létrehozva egy makroszkopikus mágneses teret. Az állandó mágneseknek van egy északi és egy déli pólusuk, és a mágneses tér vonalai az északi pólustól indulnak ki, és a déli pólusban végződnek a mágnesen kívül, míg a mágnesen belül a déli pólustól az északi pólus felé haladnak.
Elektromos áram
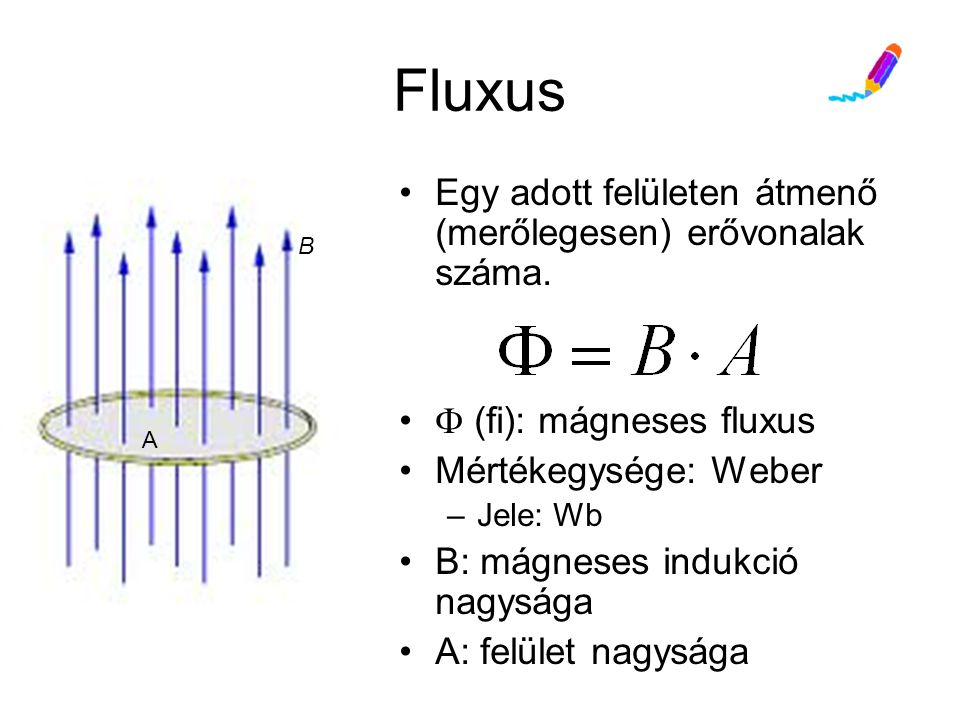
Egy másik, rendkívül fontos forrása a mágneses indukciónak az elektromos áram. Amikor elektromos töltések mozognak, mágneses teret hoznak létre maguk körül. Ezt a jelenséget írja le az Ampère-törvény. Egy egyenes, hosszú vezető körül, amelyben I áram folyik, a mágneses indukció (\\mathbf\{B\}) körkörös vonalak mentén helyezkedik el a vezető körül, és a nagysága a következőképpen adható meg:
B \= \\frac\{\\mu\_0 I\}\{2 \\pi r\}
ahol \\mu\_0 a vákuum permeabilitása (4\\pi \\times 10^\{\-7\} \\, \\text\{T\} \\cdot \\text\{m/A\}), I az áram erőssége, és r a vezetőtől mért távolság. A mágneses tér irányát itt is a jobbkéz-szabállyal határozhatjuk meg: ha a hüvelykujjunk az áram irányába mutat, akkor a begörbülő ujjaink a mágneses tér vonalainak irányát jelzik.
Elektromágnesek
Az elektromos áram mágneses hatását kihasználva hozhatunk létre elektromágneseket. Egy tekercsbe (szolenoidba) vezetett elektromos áram sokkal erősebb és irányíthatóbb mágneses teret generál, mint egy egyenes vezető. A szolenoid belsejében a mágneses tér közel homogén, és a nagysága arányos a tekercs menetszámával, az áram erősségével és fordítottan arányos a tekercs hosszával (hosszú szolenoid esetén). Az elektromágnesek kulcsfontosságúak számos technológiai alkalmazásban, a reléktől kezdve az MRI-berendezésekig.

A mágneses indukció fontos törvényei
Számos alapvető fizikai törvény írja le a mágneses indukció viselkedését és kapcsolatát más fizikai mennyiségekkel.

Faraday indukciós törvénye
A Faraday indukciós törvénye az egyik legfontosabb törvény az elektromágnesességben. Kimondja, hogy ha egy zárt vezetőhurokban megváltozik a mágneses fluxus, akkor a hurokban elektromotoros erő (EMF) indukálódik. Az indukált EMF nagysága egyenlő a mágneses fluxus időbeli változásának sebességével:
\\mathcal\{E\} \= \-\\frac\{d\\Phi\_B\}\{dt\}
A negatív előjel a Lenz-törvényt tükrözi, amely kimondja, hogy az indukált áram (és az általa létrehozott mágneses tér) olyan irányú, hogy akadályozza a fluxus változását, amely létrehozta.
Lenz törvénye
Ahogy említettük, a Lenz törvénye kiegészíti Faraday törvényét azáltal, hogy megadja az indukált áram irányát. Ha egy mágnes közeledik egy tekercshez, az indukált áram olyan mágneses teret hoz létre, amely taszítja a mágnest. Ha a mágnes távolodik, az indukált áram olyan mágneses teret hoz létre, amely vonzza a mágnest. Ez az “ellenállás” a fluxus változásával szemben az energia megmaradásának elvéből következik.
Gauss törvénye a mágnesességre
A Gauss törvénye a mágnesességre kimondja, hogy nincsenek mágneses monopólusok, azaz nincsenek olyan “mágneses töltések”, amelyekből a mágneses térvonalak kiindulnának vagy amelyekben végződnének. Matematikailag ezt úgy fejezzük ki, hogy egy zárt felületen átmenő mágneses fluxus mindig nulla:
\\oint \\mathbf\{B\} \\cdot d\\mathbf\{A\} \= 0
Ez azt jelenti, hogy a mágneses térvonalak mindig zárt hurkokat alkotnak.
Ampère törvénye (kibővítve Maxwell korrekciójával)
Az Ampère törvénye eredetileg az elektromos áram és az általa létrehozott mágneses tér közötti kapcsolatot írta le:
\\oint \\mathbf\{B\} \\cdot d\\mathbf\{l\} \= \\mu\_0 I\_\{enc\}
ahol az integrál egy zárt görbe mentén történik, és I\_\{enc\} a görbe által körülvett áram. Maxwell kiegészítette ezt a törvényt a eltolási áram fogalmával, hogy figyelembe vegye a változó elektromos mezők mágneses hatását is. A Maxwell-Ampère törvény kibővített formája:
\\oint \\mathbf\{B\} \\cdot d\\mathbf\{l\} \= \\mu\_0 \\left\(I\_\{enc\} \+ \\epsilon\_0 \\frac\{d\\Phi\_E\}\{dt\}\\right\)
ahol \\epsilon\_0 a vákuum permittivitása, és \\frac\{d\\Phi\_E\}\{dt\} az elektromos fluxus időbeli változásának sebessége.
Kísérletek a mágneses indukció bemutatására
A mágneses indukció jelensége látványos kísérletekkel demonstrálható, amelyek segítenek a fogalom intuitív megértésében.
Mágnes mozgatása tekercsben
Egy egyszerű, de szemléletes kísérlet, ha egy állandó mágnest mozgatunk egy tekercs belsejében vagy annak közelében. Ha a mágnest a tekercsbe toljuk, a tekercsben feszültség indukálódik, és ha egy zárt áramkör részét képezi a tekercs, akkor áram is folyik. Amikor a mágnes áll, nincs indukált feszültség vagy áram. Ha a mágnest kihúzzuk a tekercsből, ismét feszültség indukálódik, de az ellenkező polaritással, ami fordított irányú áramot eredményez.
Két tekercs kísérlete
Egy másik klasszikus kísérlet két egymás közelében elhelyezett tekercset használ. Ha az egyik tekercsben (primer tekercs) változtatjuk az áramot (például be- vagy kikapcsoljuk, vagy a nagyságát változtatjuk), akkor a változó mágneses fluxus a másik tekercsen (szekunder tekercs) keresztül is áthalad, és abban feszültséget indukál. Ez az elv áll a transzformátorok működésének hátterében.
A mágneses indukció alkalmazásai
A mágneses indukció elvén számos nélkülözhetetlen technológiai eszköz és berendezés működik.
Elektromos generátorok
Az elektromos generátorok mechanikai energiát alakítanak át elektromos energiává a mágneses indukció segítségével. Egy vezetőhurkot (vagy tekercset) egy mágneses térben forgatnak, vagy egy mágneses teret forgatnak egy álló vezetőhurok körül. Mindkét esetben a vezetőhurkon áthaladó mágneses fluxus változik, ami elektromotoros erőt (feszültséget) indukál a hurokban. Ez az
Az Elektromos Aram Magneses Hatasa Ppt
Az Elektromos Áram Mágneses Hatása: A Tudomány és Technológia Alapköve
Az elektromos áram mágneses hatása a fizika egyik alapvető jelensége, amely áthatja mindennapi életünket a legegyszerűbb elektromos eszközöktől a legösszetettebb technológiákig. Ez a látszólag egyszerű kapcsolat az elektromosság és a mágnesség között forradalmasította a tudományt és a technikát, lehetővé téve olyan találmányokat, mint az elektromotor, a generátor és a transzformátor. Ebben a részletes tanulmányban mélyrehatóan feltárjuk ennek a lenyűgöző jelenségnek a hátterét, a hozzá kapcsolódó kísérleteket, elméleteket és gyakorlati alkalmazásokat.
Az Elektromágnesség Történeti Gyökerei
Az elektromosság és a mágnesség közötti kapcsolat megértésének útja évszázadokon átívelő felfedezések sorozata volt. Kezdetben a két jelenséget teljesen különállónak tekintették. A sztatikus elektromosság jelenségeit már az ókorban ismerték, ahogy a borostyánkő dörzsölésével apró tárgyakat lehetett vonzani. A természetes mágnesesség, amelyet a magnetit ásvány mutat, szintén régóta ismert jelenség volt. Azonban a kettő közötti valódi kapcsolat csak a 19. század elején vált nyilvánvalóvá.
Hans Christian Ørsted Forradalmi Kísérlete (1820)
A sorsdöntő áttörést Hans Christian Ørsted dán fizikus 1820-as kísérlete hozta meg. Egy véletlennek köszönhetően Ørsted észrevette, hogy amikor egy árammal átfolyó vezeték közelében elhelyezett iránytű tűje elmozdult. Ez volt az első kísérleti bizonyíték arra, hogy az elektromos áram mágneses teret hoz létre. Ørsted publikációja hatalmas izgalmat váltott ki a tudományos közösségben, és elindította az elektromágnesség intenzív kutatását.
Ørsted Kísérletének Részletei
Ørsted kísérletében egy egyszerű áramkört használt, amely egy galvánelemből, vezetékekből és egy kapcsolóból állt. Amikor az áramkör zárult, és áram kezdett folyni a vezetékben, az a vezeték közelében elhelyezett iránytű tűje merőlegesen állt be a vezetékre. Amikor az áramot kikapcsolták, a tű visszatért eredeti, észak-déli irányába. Ez egyértelműen megmutatta, hogy az elektromos áram valamilyen módon mágneses hatást fejt ki a környezetére.
André-Marie Ampère További Vizsgálatai
André-Marie Ampère francia fizikus lelkesen vetette bele magát az Ørsted felfedezése nyomán felmerült kérdésekbe. Ampère kiterjedt kísérleteket végzett az árammal átfolyó vezetékek közötti kölcsönhatásokra. Felfedezte, hogy két párhuzamos, azonos irányban áramot vezető vezeték vonzza egymást, míg ha az áram iránya ellentétes, akkor taszítják egymást. Ez a jelenség analóg a mágneses pólusok közötti kölcsönhatáshoz.
Ampère Törvénye
Ampère munkásságának egyik csúcspontja az Ampère törvényének megalkotása volt, amely kvantitatív kapcsolatot ír le az elektromos áram és az általa létrehozott mágneses tér között. A törvény integrális formában a következőképpen fejezhető ki:
$$\oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{enc}$$
ahol $\mathbf{B}$ a mágneses indukció, $d\mathbf{l}$ az integrálás vonaleleme, $\mu_0$ a vákuum permeabilitása, és $I_{enc}$ a zárt görbe által körülvett áram. Ez a törvény alapvető fontosságú az elektromágneses jelenségek megértéséhez és a mágneses mezők számításához.
Michael Faraday és az Elektromágneses Indukció
Michael Faraday angol tudós nevéhez fűződik az elektromágneses indukció felfedezése 1831-ben. Faraday megmutatta, hogy egy változó mágneses tér elektromos áramot indukálhat egy vezetőben. Ez a felfedezés nemcsak az elektromágnesség megértésének egy újabb mérföldköve volt, hanem a modern elektromos technológia alapjait is megteremtette.
Faraday Indukciós Törvénye
Faraday indukciós törvénye szerint az indukált elektromotoros erő (EMF) egy zárt áramkörben egyenlő a mágneses fluxus időbeli változásának negatívjával:
$$\mathcal{E} = -\frac{d\Phi_B}{dt}$$
ahol $\mathcal{E}$ az indukált elektromotoros erő, és $\Phi_B$ a mágneses fluxus. Ez a törvény magyarázza a generátorok működését, amelyek mechanikai energiát alakítanak át elektromos energiává.
James Clerk Maxwell és az Elektromágneses Elmélet Egyesítése
James Clerk Maxwell skót fizikus az 1860-as években egyesítette az addig ismert elektromos és mágneses jelenségeket egy átfogó elektromágneses elméletbe. Maxwell négy egyenlete, a Maxwell-egyenletek, leírják az elektromos és mágneses mezők viselkedését és kölcsönhatásait, valamint azt, hogy a fény elektromágneses hullám. Maxwell munkája nemcsak az elektromágnesség megértésének csúcspontja volt, hanem a modern fizika egyik alappillére is.
A Maxwell-egyenletek

A Maxwell-egyenletek differenciális formában a következők:
- Gauss törvénye az elektromosságról: $$\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0}$$
- Gauss törvénye a mágnességről: $$\nabla \cdot \mathbf{B} = 0$$
- Faraday indukciós törvénye: $$\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}$$
- Ampère-Maxwell törvény: $$\nabla \times \mathbf{B} = \mu_0 \left( \mathbf{J} + \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} \right)$$
ahol $\mathbf{E}$ az elektromos térerősség, $\mathbf{B}$ a mágneses indukció, $\rho$ a töltéssűrűség, $\mathbf{J}$ az áramsűrűség, $\epsilon_0$ a vákuum permittivitása, és $\mu_0$ a vákuum permeabilitása.
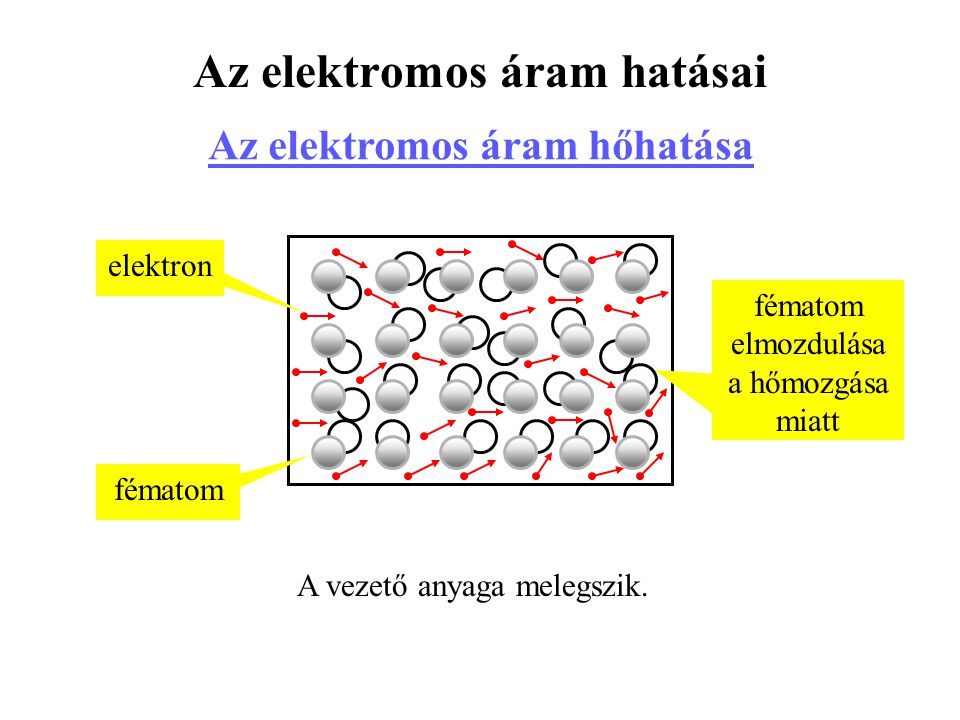
Az Elektromos Áram Mágneses Hatásának Fizikai Alapjai
Ahhoz, hogy mélyebben megértsük az elektromos áram mágneses hatását, meg kell vizsgálnunk a mögöttes fizikai elveket. Amikor elektromos áram folyik egy vezetőben, valójában elektromos töltések (általában elektronok) mozognak. Ezek a mozgó töltések hozzák létre a mágneses teret a vezető körül.
A Biot-Savart Törvény
A Biot-Savart törvény egy matematikai egyenlet, amely leírja egy árammal átfolyó vezeték egy kis szegmense által létrehozott mágneses teret egy adott pontban. A törvény szerint a mágneses tér $d\mathbf{B}$ egy $I d\mathbf{l}$ áramszegmens által egy $\mathbf{r}$ vektorral távolabbi pontban a következőképpen adható meg:
$$d\mathbf{B} = \frac{\mu_0}{4\pi} \frac{I d\mathbf{l} \times \mathbf{\hat{r}}}{r^2}$$
ahol $I$ az áram erőssége, $d\mathbf{l}$ az áramszegmens vektor, $\mathbf{r}$ a vektor az áramszegmenstől a megfigyelési pontig, $\mathbf{\hat{r}}$ az $\mathbf{r}$ irányába mutató egységvektor, és $\mu_0$ a vákuum permeabilitása.
A Mágneses Tér Vonalai
A mágneses teret gyakran mágneses térvonalakkal szemléltetjük. Ezek olyan képzeletbeli vonalak, amelyek minden pontban a mágneses indukció $\mathbf{B}$ irányába mutatnak. Az árammal átfolyó egyenes vezeték körül a mágneses térvonalak koncentrikus körök, amelyek középpontja a vezeték tengelyében van. A mágneses tér erőssége a vezetékhez közelebb nagyobb, és távolodva csökken. A mágneses tér irányát a jobbkéz-szabállyal lehet meghatározni: ha a jobb kezünk hüvelykujja az áram irányába mutat, akkor a begörbülő ujjaink a mágneses térvonalak irányát jelzik.
Mágneses Erő Árammal Átfolyó Vezetőre
Ha egy árammal átfolyó vezető mágneses térbe kerül, akkor mágneses erő hat rá. Ennek az erőnek az iránya merőleges mind az áram irányára, mind a mágneses tér irányára, és nagysága a következőképpen adható meg:

$$\mathbf{F} = I \mathbf{l} \times \mathbf{B}$$
ahol $\mathbf{F}$ a mágneses erő, $I$ az áram erőssége, $\mathbf{l}$ a vezető árammal átfolyó szakaszának vektora (irányával megegyezik az áram irányával), és $\mathbf{B}$ a külső mágneses tér.
Az Elektromos Áram Mágneses Hatásának Kísérleti Bemutatása
Számos klasszikus kísérlet szemlélteti az elektromos áram mágneses hatását.
Az Iránytű Elhajlása Áram Hatására
Ahogy azt Ørsted is megfigyelte, egy árammal átfolyó vezeték közelében elhelyezett iránytű tűje elhajlik. Ez a legegyszerűbb módja annak, hogy demonstráljuk az áram mágneses hatását. A tű elhajlásának iránya függ az áram irányától és a vezeték irányához viszonyított helyzetétől.
Két Párhuzamos Vezeték Kölcsönhatása
Amint azt Ampère felfedezte, két párhuzamos, árammal átfolyó vezeték erővel hat egymásra. Ha az áramok azonos irányúak, a vezetékek vonzzák egymást. Ha az áramok ellentétes irányúak, a vezetékek taszítják egymást. Ennek az erőnek a nagysága arányos a vezetékekben folyó áramok szorzatával és a vezetékek hosszával, és fordítottan arányos a köztük lévő távolsággal.
A Tekercs Mágneses Tere (Szolenoid)
Ha egy vezetéket tekercs alakúra formálunk (ezt szolenoidnak nevezzük), az áram mágneses hatása felerősödik. A szolenoid belsejében a mágneses tér közelítőleg homogén és párhuzamos a tekercs tengelyével. A szolenoidon kívül a mágneses tér hasonlít egy rúd mágnes teréhez, és északi és déli pólusa van. A szolenoid mágneses terének erőssége arányos a tekercs menetszámával, az áram erősségével és fordítottan arányos a tekercs hosszával.
A Szolenoid Mágneses Terének Képlete
Egy ideális, végtelen hosszú szolenoid belsejében a mágneses tér erőssége:
$$B = \mu_0 n I$$
ahol $n = N/L$ a menetsűrűség (a menetszám per egységnyi hosszúság), és $I$ az áram erőssége.
Az Elektromágnesesség Alkalmazásai a Technikában
Az elektromos áram mágneses hatásának felfedezése és az elektromágnesség elméletének kidolgozása a modern technológia számtalan területén alapvető fontosságúvá vált.
Elektromágnesek
Az elektromágnesek olyan mágnesek, amelyek mágneses terét elektromos áram hozza létre. Általában egy vasmag köré tekercselt huzalból állnak. Amikor áram folyik a huzalban, a vasmag felmágneseződik, létrehozva egy erős mágneses teret. Az elektromágnesek előnye, hogy mágneses erejük az áram erősségének változtatásával szabályozható, és az áram kikapcsolásával a mágnesesség megszűnik. Széles körben alkalmazzák őket darukban, mágneszárakban, hangszórókban és sok más eszközben.
Elektromotorok
Az elektromotorok olyan eszközök, amelyek elektromos energiát alakítanak át mechanikai energiává az elektromos áram mágneses hatásának felhasználásával. Egy tipikus elektromotorban egy árammal átfolyó tekercs (a rotor) egy állandó mágneses térben vagy egy másik elektromágneses térben forog. A tekercsre ható mágneses erő forgatónyomatékot hoz létre, amely a rotort forgatja. Elektromotorokat használnak a háztartási gépektől az ipari berendezéseken át az elektromos járművekig.
Elektromos Generátorok
Az elektromos generátorok az elektromágneses indukció elvén működnek, és mechanikai energiát alakítanak át elektromos energiává. Egy tipikus generátorban egy tekercset vagy egy mágnest mozgatnak egy mágneses térben vagy egy tekercs közelében, ami elektromos áramot indukál a tekercsben. A generátorok alapvető fontosságúak az elektromos energia előállításában, legyen szó akár erőművekről, akár hordozható generátorokról.
Transzformátorok
A transzformátorok olyan passzív elektromos eszközök, amelyek két vagy több tekercs segítségével változtatják meg a váltakozó feszültséget és áramot anélkül, hogy megváltoztatnák a frekvenciát. A működésük az elektromágneses indukción alapul. Egy váltakozó áram az egyik tekercsben (a primer tekercsben) változó mágneses teret hoz létre, amely indukál egy váltakozó feszültséget a másik tekercsben (a szekunder tekercsben). A transzform
Arammal Atjart Vezet Magneses Tere

Az Árammal Átjárt Vezető Mágneses Tere – A Tudomány Mélyére Hatolva
Ebben a kimerítő cikkben részletesen feltárjuk az árammal átjárt vezető körül kialakuló mágneses teret. Megvizsgáljuk a jelenség mögött rejlő alapvető fizikai törvényeket, bemutatjuk a kísérleti bizonyítékokat, és feltárjuk a gyakorlati alkalmazások széles skáláját. Célunk, hogy egy átfogó és érthető képet nyújtsunk erről a kulcsfontosságú elektromágneses jelenségről.
Az Elektromosság és a Magnetizmus Kapcsolata – Egy Történelmi Áttekintés
Az elektromosság és a magnetizmus közötti kapcsolat megértése a fizika egyik legjelentősebb áttörése volt. Bár a két jelenséget korábban különállóként kezelték, számos kísérlet és megfigyelés rávilágított mély összefüggéseikre. Hans Christian Ørsted 1820-as híres kísérlete volt az egyik első, amely közvetlenül kimutatta, hogy az árammal átjárt vezető mágneses teret hoz létre. Ő azt tapasztalta, hogy egy iránytű tűje eltérül egy árammal átjárt vezeték közelében, ami egyértelműen jelezte a mágneses hatást.
Ørsted Kísérlete és Következményei
Ørsted kísérlete forradalmi jelentőségű volt, mivel megcáfolta azt a korábbi elképzelést, hogy az elektromosság és a magnetizmus független jelenségek. A kísérlet egyszerűsége ellenére mélyreható következményei voltak a fizika fejlődésére. Ez a megfigyelés indította el az elektromágnesség intenzív kutatását, amely olyan alapvető törvények felfedezéséhez vezetett, mint Ampère törvénye és Faraday indukciós törvénye.
Az Árammal Átjárt Egyenes Vezető Mágneses Tere
Kezdjük a legegyszerűbb esettel: egy egyenes, hosszú vezetővel, amelyen áram folyik. Kísérletek azt mutatják, hogy az ilyen vezető körül koncentrikus körök alakjában mágneses tér jön létre. A mágneses tér vonalainak iránya a jobbkéz-szabállyal határozható meg: ha a jobb kezünk hüvelykujja az áram irányába mutat, akkor a begörbülő ujjaink a mágneses tér vonalainak irányát jelzik.
A Biot-Savart Törvény
A Biot-Savart törvény egy fundamentális törvény az elektromágnességben, amely lehetővé teszi, hogy kiszámítsuk egy árammal átjárt vezető egy kis szakasza által létrehozott mágneses tér $\mathbf{dB}$ értékét egy adott pontban. A törvény szerint:
$$\mathbf{dB} = \frac{\mu_0}{4\pi} \frac{I d\mathbf{l} \times \mathbf{r}}{r^3}$$
ahol:
- $\mathbf{dB}$ a mágneses tér infinitezimális eleme,
- $\mu_0$ a vákuum permeabilitása ($4\pi \times 10^{ -7} \, \text{T}\cdot\text{m/A}$),
- $I$ az áram erőssége a vezetőben,
- $d\mathbf{l}$ a vezető egy infinitezimális hosszúságú vektoreleme az áram irányában,
- $\mathbf{r}$ a vektor a vezető $d\mathbf{l}$ elemétől a megfigyelési pontig,
- $r$ a vektor $\mathbf{r}$ nagysága.
Az Egyenes Hosszú Vezető Mágneses Terének Számítása
A Biot-Savart törvény integrálásával megkaphatjuk egy egyenes, hosszú vezető által létrehozott mágneses tér nagyságát egy tőle $r$ távolságra lévő pontban:

$$B = \frac{\mu_0 I}{2\pi r}$$
Ez az egyenlet azt mutatja, hogy a mágneses tér erőssége egyenesen arányos az áram erősségével ($I$) és fordítottan arányos a vezetőtől való távolsággal ($r$). A mágneses tér vonalai koncentrikus körök a vezető körül, és a tér erőssége a vezetőtől távolodva csökken.
Az Árammal Átjárt Körhurok Mágneses Tere
Vizsgáljuk meg most egy árammal átjárt körhurok által létrehozott mágneses teret. Egy ilyen hurok is mágneses teret generál, amelynek alakja bonyolultabb, mint egy egyenes vezetőé. A hurok középpontjában a mágneses tér vonalai közelítőleg egyenesek és merőlegesek a hurok síkjára.

A Körhurok Középpontjában Lévő Mágneses Tér
Egy $R$ sugarú, $I$ áramot vezető körhurok középpontjában a mágneses tér nagysága a Biot-Savart törvény alkalmazásával számítható ki:
$$B = \frac{\mu_0 I}{2 R}$$
A mágneses tér iránya ismét a jobbkéz-szabállyal határozható meg: ha a jobb kezünk ujjai az áram irányába görbülnek a hurokban, akkor a kinyújtott hüvelykujjunk a mágneses tér irányát mutatja a hurok középpontjában.
A Körhurok Mágneses Terének Általános Esete
A körhurok síkjától távolabbi pontokban a mágneses tér képlete bonyolultabb. Azonban általánosságban elmondható, hogy a körhurok mágneses tere dipólus jellegű, ami azt jelenti, hogy távolról úgy viselkedik, mint egy kis rúdmágnes, és rendelkezik északi és déli pólussal.
A Tekercs (Solenoid) Mágneses Tere
Ha több körhurkot egymás mellé helyezünk és összekapcsolunk, egy tekercset (vagy szolenoidot) kapunk. Az árammal átjárt tekercs mágneses tere sokkal erősebb és homogénabb lehet a belsejében, mint egyetlen huroké.
Az Ideális Szolenoid Mágneses Tere
Egy ideális szolenoid egy végtelen hosszú, szorosan tekercselt huzalból álló tekercs. Egy ilyen ideális szolenoid belsejében a mágneses tér homogén és párhuzamos a szolenoid tengelyével, míg kívül a mágneses tér elhanyagolhatóan kicsi. A szolenoid belsejében a mágneses tér nagysága:
$$B = \mu_0 n I$$
ahol $n$ a menetsűrűség (a menetek száma az egységnyi hosszon, $n = N/l$, ahol $N$ a teljes menetszám és $l$ a szolenoid hossza), és $I$ az áram erőssége.
A Véges Hosszúságú Szolenoid Mágneses Tere
A valóságban a szolenoidok véges hosszúságúak. Egy véges hosszúságú szolenoid mágneses tere a végeinél gyengébb és nem teljesen homogén. A mágneses tér pontos kiszámítása bonyolultabb integrálást igényel, de a lényeg megmarad: a szolenoid belsejében a mágneses tér erősebb, mint egyetlen huroké, és a menetsűrűséggel arányos.
A Toroid Mágneses Tere
Egy toroid egy olyan tekercs, amelyet egy tórusz (egy fánk alakú felület) mentén tekercselnek fel. Az árammal átjárt toroid mágneses tere a toroid belsejére korlátozódik, és a külső tér elhanyagolhatóan kicsi.
A Toroid Belsejében Lévő Mágneses Tér
Egy $N$ menetszámú, $r$ belső és $R$ külső sugárral rendelkező toroid belsejében, a középsugártól (körülbelül $(r+R)/2$) távol nem lévő pontokban a mágneses tér nagysága:
$$B = \frac{\mu_0 N I}{2\pi \rho}$$

ahol $\rho$ a tórusz tengelyétől mért távolság. Ez az egyenlet azt mutatja, hogy a mágneses tér a toroid belsejében nem teljesen homogén, hanem fordítottan arányos a távolsággal a tengelytől.
Ampère Törvénye – Egy Általánosabb Megközelítés
Ampère törvénye egy másik alapvető törvény az elektromágnességben, amely kapcsolatot teremt az áramok és az általuk létrehozott mágneses tér között. Integrális formában Ampère törvénye így szól:
$$\oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{enc}$$
ahol az integrál egy tetszőleges zárt görbe mentén vett vonalintegrálja a mágneses térnek ($\mathbf{B}$), $d\mathbf{l}$ a görbe infinitezimális hosszúságú vektoreleme, és $I_{enc}$ a görbe által körülvett teljes áram.
Ampère Törvényének Alkalmazása
Ampère törvénye különösen hasznos olyan szimmetrikus árameloszlások mágneses terének kiszámításához, mint az egyenes hosszú vezető, a szolenoid és a toroid. A törvény alkalmazásához ki kell választanunk egy olyan zárt Ampère-féle hurkot, amely kihasználja a szimmetriát, így az integrál könnyen elvégezhető.
Az Árammal Átjárt Vezetők Közötti Erőhatás
Ha két árammal átjárt vezető egymás közelében helyezkedik el, akkor mindkettő mágneses teret hoz létre, és ez a mágneses tér erőhatást gyakorol a másik vezetőben folyó áramra. Ez az erőhatás az Lorentz-erő speciális esete.
Párhuzamos Vezetők Esetén
Két párhuzamos, $d$ távolságra lévő vezető esetén, amelyekben $I_1$ és $I_2$ áram folyik, az egyik vezetőre a másik által kifejtett erő hosszegységenként:
$$F/l = \frac{\mu_0 I_1 I_2}{2\pi d}$$
Ha az áramok azonos irányúak, az erő vonzó jellegű; ha ellentétes irányúak, az erő taszító.
Gyakorlati Alkalmazások
Az árammal átjárt vezetők mágneses terének jelensége számos technológiai alkalmazás alapját képezi:
- Elektromágnesek: A tekercsek (szolenoidok) erős mágneses teret hoznak létre, amelyeket sokféle célra használnak, például darukban, mágneszárakban és orvosi képalkotó eljárásokban (MRI).
- Elektromos motorok: Az elektromos motorok az árammal átjárt vezetők mágneses terének egymásra hatásán alapulnak, ami forgatónyomatékot hoz létre.
- Hangszórók: A hangszórókban egy árammal átjárt tekercs mágneses tere kölcsönhatásba lép egy állandó mágnes terével, ami a membrán rezgését és hangot eredményez.
- Indukciós eszközök: Az elektromágneses indukció elvén működő eszközök, mint például a transzformátorok, szintén az árammal átjárt vezetők által létrehozott változó mágneses teret használják ki.


Összefoglalás
Az árammal átjárt vezető mágneses tere egy alapvető jelenség az elektromágnességben, amelynek megértése elengedhetetlen a modern technológia számos területén. A Biot-Savart törvény és Ampère törvénye kulcsfontosságú eszközök a mágneses tér jellemzőinek kiszámításához különböző geometriájú vezetők esetén. A jelenség gyakorlati alkalmazásai rendkívül sokrétűek, az egyszerű elektromágnesektől a komplex elektromos motorokig és orvosi berendezésekig terjednek.
További Kutatási Lehetőségek
Az elektromágnesség területe továbbra is aktív kutatási terület. A kutatók folyamatosan keresik az új alkalmazási lehetőségeket és a jelenségek mélyebb megértését, beleértve a szupravezető anyagok mágneses terének viselkedését és az elektromágneses hullámok terjedését.
Kísérletek Otthon
Egyszerű kísérletekkel otthon is szemléltethető az árammal átjárt vezető mágneses tere. Például egy iránytű segítségével megfigyelhető a mágneses tér egy árammal átjárt huzal körül. Ezek a kísérletek segítenek a fogalmak gyakorlati megértésében.
A Jövő Perspektívái
Az elektromágnesség és az árammal átjárt vezetők mágneses tere továbbra is kulcsszerepet fognak játszani a jövő technológiájában, beleértve az energiaátvitelt, a közlekedést és az információs technológiát.