Munka Energia Teljesitmeny Hatasfok Feladatok

A Munka, Energia, Teljesítmény és Hatásfok Mélyreható Tanulmányozása

Ebben a részletes cikkben átfogóan vizsgáljuk a fizika négy alapvető fogalmát: a munkát, az energiát, a teljesítményt és a hatásfokot. Célunk, hogy ne csupán definíciókat adjunk, hanem mélyrehatóan megértsük ezen fogalmak közötti összefüggéseket, gyakorlati alkalmazásaikat és a hozzájuk kapcsolódó számítási módszereket. Számos példán és kidolgozott feladaton keresztül segítjük az olvasót a téma alapos elsajátításában.

1. A Munka Fogalma a Fizikában

A fizikában a munka akkor végezhető, ha egy erő egy testet elmozdít. Fontos megjegyezni, hogy pusztán egy erő hatása nem feltétlenül jelent munkavégzést; az elmozdulás elengedhetetlen. Matematikailag a munka (W) egy állandó \\mathbf\{F\} erő által végzett munkát, amely egy testet egyenes vonalban \\mathbf\{d\} vektorral elmozdít, a következőképpen definiáljuk:

\\mathbf\{W\} \= \\mathbf\{F\} \\cdot \\mathbf\{d\} \= \|\\mathbf\{F\}\| \|\\mathbf\{d\}\| \\cos \\theta

ahol \|\\mathbf\{F\}\| az erő nagysága, \|\\mathbf\{d\}\| az elmozdulás nagysága, és \\theta az erő és az elmozdulás vektorai közötti szög. A munka SI mértékegysége a joule (J), amely megegyezik egy newton méterrel (N·m).

1.1. Pozitív, Negatív és Nulla Munka

A végzett munka lehet pozitív, negatív vagy nulla, attól függően, hogy az erő és az elmozdulás vektorai milyen szöget zárnak be egymással.

• Pozitív munka: Ha az erőnek az elmozdulás irányába eső komponense van (\\theta < 90^\\circ), a munka pozitív. Például, amikor egy izom összehúzódik és megemel egy súlyt, az izom által kifejtett erő pozitív munkát végez a súlyon.
• Negatív munka: Ha az erőnek az elmozdulással ellentétes irányú komponense van (90^\\circ < \\theta \\le 180^\\circ), a munka negatív. Például, amikor egy súlyt lassan leengedünk, a gravitációs erő negatív munkát végez a súlyon (az elmozdulás felfelé, a gravitációs erő lefelé irányul). A súrlódási erő is negatív munkát végez, mivel mindig a mozgással ellentétes irányú.
• Nulla munka: Ha az erő merőleges az elmozdulásra (\\theta \= 90^\\circ), vagy ha nincs elmozdulás (\|\\mathbf\{d\}\| \= 0), a munka nulla. Például, egy vízszintes felületen egyenletes sebességgel haladó testre ható függőleges tartóerő nem végez munkát, mert az erő merőleges az elmozdulásra. Továbbá, ha valaki egy nehéz tárgyat tart a helyén anélkül, hogy elmozdulna, nem végez munkát a tárgyon, annak ellenére, hogy erőt fejt ki.

1.2. Változó Erő Munkája

Ha az erő nem állandó, vagy az elmozdulás nem egyenes vonalú, a végzett munkát integrálással számíthatjuk ki. Egy egydimenziós esetben, ha egy F\(x\) erő hat egy testre, miközben az x\_1 pozícióból az x\_2 pozícióba mozdul el, a végzett munka:

W \= \\int\_\{x\_1\}^\{x\_2\} F\(x\) \\, dx

Három dimenzióban ez az integrál egy görbe mentén történik:

W \= \\int\_\{\\mathbf\{r\}\_1\}^\{\\mathbf\{r\}\_2\} \\mathbf\{F\} \\cdot d\\mathbf\{r\}

ahol d\\mathbf\{r\} az infiniteszimális elmozdulásvektor a pálya mentén.

1.3. Példák a Munkavégzésre

• Egy ember egy nehéz dobozt tol a padlón. A tolóerő munkát végez a dobozon, ha az elmozdul. A súrlódási erő negatív munkát végez.
• Egy lift felemel egy személyt. A lift kábelének húzóereje pozitív munkát végez a személyen. A gravitációs erő negatív munkát végez.
• Egy műhold kering a Föld körül. A gravitációs erő (ami ebben az esetben centripetális erő) nem végez munkát a műholdon, mert az erő mindig merőleges a sebességre (és így az infiniteszimális elmozdulásra).

2. Az Energia Fogalma és Formái

Az energia egy rendszer azon képessége, hogy munkát végezzen. Skalár mennyiség, és SI mértékegysége szintén a joule (J). Az energia számos formában létezhet, és az egyik formából a másikba alakulhat át. A munkatétel alapvető fontosságú az energia és a munka közötti kapcsolat megértéséhez. Kimondja, hogy egy testre ható összes erő által végzett munka egyenlő a test kinetikus energiájának megváltozásával:

W\_\{összes\} \= \\Delta K \= K\_f \- K\_i \= \\frac\{1\}\{2\}mv\_f^2 \- \\frac\{1\}\{2\}mv\_i^2

ahol m a test tömege, v\_i a kezdeti sebesség és v\_f a végső sebesség.

2.1. Kinetikus Energia

A kinetikus energia (K) egy mozgó test energiája, amely a tömegétől (m) és a sebességének a négyzetétől (v) függ:

K \= \\frac\{1\}\{2\}mv^2

Minél nagyobb egy test tömege vagy sebessége, annál nagyobb a kinetikus energiája.

2.2. Potenciális Energia

A potenciális energia egy test helyzetéből vagy konfigurációjából adódó tárolt energia. Különböző típusai léteznek:

• Gravitációs potenciális energia (U\_g): Egy m tömegű test gravitációs potenciális energiája a Föld felszínéhez képest h magasságban:

  U\_g \= mgh

  ahol g a gravitációs gyorsulás.

• Rugalmas potenciális energia (U\_e): Egy k rugóállandójú rugóban tárolt energia, ha x távolsággal megnyújtjuk vagy összenyomjuk a nyugalmi helyzetéhez képest:

  U\_e \= \\frac\{1\}\{2\}kx^2

• Elektromos potenciális energia: Elektromos töltések közötti kölcsönhatásból származó energia.
• Kémiai potenciális energia: Az atomok és molekulák közötti kémiai kötésekben tárolt energia.
• Nukleáris potenciális energia: Az atommagban tárolt energia.

2.3. Az Energia Megmaradásának Törvénye

Az egyik legfontosabb természeti törvény az energia megmaradásának törvénye, amely kimondja, hogy egy zárt rendszer teljes energiája állandó marad, bár az energia egyik formából a másikba alakulhat át. Matematikailag:

E\_\{kezdeti\} \= E\_\{végső\}

Például, egy leeső labda gravitációs potenciális energiája fokozatosan kinetikus energiává alakul át (a légellenállást elhanyagolva). A teljes mechanikai energia (E \= K \+ U) állandó marad.

3. A Teljesítmény Definíciója és Jelentősége

A teljesítmény (P) a munka végzésének sebességét vagy az energiaátalakulás sebességét adja meg. Más szóval, megmutatja, hogy milyen gyorsan végeznek munkát vagy alakítanak át energiát. Matematikailag:

P \= \\frac\{W\}\{t\} \= \\frac\{dE\}\{dt\}

ahol W a végzett munka, t az idő, E az energia és t az idő. A teljesítmény SI mértékegysége a watt (W), amely megegyezik egy joule per szekundummal (J/s).

3.1. Átlagos és Pillanatnyi Teljesítmény

• Átlagos teljesítmény: Az összes végzett munka osztva az eltelt idővel:

  P\_\{átlagos\} \= \\frac\{\\Delta W\}\{\\Delta t\}

• Pillanatnyi teljesítmény: A teljesítmény egy adott pillanatban, ami a munka idő szerinti deriváltja:

  P \= \\lim\_\{\\Delta t \\to 0\} \\frac\{\\Delta W\}\{\\Delta t\} \= \\frac\{dW\}\{dt\}

  Ha egy \\mathbf\{F\} erő hat egy testre, amely \\mathbf\{v\} sebességgel mozog, a pillanatnyi teljesítmény kifejezhető a következőképpen is:

  

  P \= \\mathbf\{F\} \\cdot \\mathbf\{v\} \= \|\\mathbf\{F\}\| \|\\mathbf\{v\}\| \\cos \\phi

  ahol \\phi az erő és a sebesség vektorai közötti szög.

3.2. A Teljesítmény Gyakorlati Alkalmazásai

A teljesítmény fogalma kulcsfontosságú számos területen, például a gépészetben (motorok teljesítménye), az elektromosságban (elektromos eszközök fogyasztása) és a biológiában (izomzat által kifejtett teljesítmény).

• Egy autó motorjának teljesítménye megmutatja, hogy milyen gyorsan képes munkát végezni a jármű gyorsításához vagy emelkedőn való feljutáshoz.
• Egy izzó teljesítménye (wattban megadva) azt jelzi, hogy másodpercenként mennyi elektromos energiát alakít át fény- és hőenergiává.

4. A Hatásfok Fogalma és Számítása

A hatásfok (\\eta) egy rendszer vagy folyamat hatékonyságának mértéke. Azt adja meg, hogy a befektetett energia vagy végzett munka mekkora része hasznos munkává vagy a kívánt energiaformává alakul át. A hatásfok egy dimenzió nélküli mennyiség, amelyet gyakran százalékban adnak meg. Matematikailag:

\\eta \= \\frac\{\\text\{Hasznos kimenet\}\}\{\\text\{Befektetett bemenet\}\} \= \\frac\{W\_\{hasznos\}\}\{W\_\{befektetett\}\} \= \\frac\{E\_\{hasznos\}\}\{E\_\{befektetett\}\} \= \\frac\{P\_\{hasznos\}\}\{P\_\{befektetett\}\}

Mivel a kimenet sosem lehet nagyobb a bemenetnél (az energiamegmaradás törvénye miatt), a hatásfok mindig kisebb vagy egyenlő 1-gyel (vagy 100%-kal).

4.1. Példák a Hatásfokra

• Egy villanymotor hatásfoka megmutatja, hogy a felvett elektromos energia mekkora hányada alakul át mechanikai munkává. A maradék energia általában hő formájában veszik el.
• Egy hőerőgép hatásfoka azt jelzi, hogy a befektetett hőenergia mekkora része alakul át mechanikai munkává. A Carnot-ciklus adja meg a hőerőgépek elméleti maximális hatásfokát.
• Egy napelem hatásfoka azt mutatja meg, hogy a beeső napfény energiájának mekkora hányadát alakítja át elektromos energiává.

4.2. A Hatásfok Növelésének Fontossága

A hatásfok növelése számos szempontból fontos. Gazdasági szempontból kevesebb bemeneti energiára van szükség ugyanazon hasznos kimenet eléréséhez, ami költségmegtakarítást eredményez. Környezetvédelmi szempontból a magasabb hatásfok kevesebb energiafelhasználást jelent, ami csökkenti a természeti erőforrások kimerülését és a környezetszennyezést.

5. Kapcsolat a Munka, Energia, Teljesítmény és Hatásfok Között

Ezek a négy fogalom szorosan összefügg egymással. A munka az energiaátadás egyik formája. Az energia a munkavégzés képessége. A teljesítmény a munka végzésének vagy az energiaátalakulás sebessége. A hatásfok pedig azt méri, hogy ez az energiaátalakulás mennyire hatékony.

Gyakran egy rendszerbe energiát fektetünk be, amely munkát végez. A teljesítmény megadja, hogy ez a munkavégzés milyen gyorsan történik, a hatásfok pedig azt, hogy a befektetett energia mekkora része fordítódik hasznos munkára.

6. Gyakorlati Feladatok a Munka, Energia, Teljesítmény és Hatásfok Témakörében

Az alábbiakban néhány gyakorlati feladatot talál, amelyek segítenek elmélyíteni a fent tárgyalt fogalmak megértését.

6.1. Munka Feladatok

1. Egy 50 kg tömegű dobozt vízszintes felületen 10 m távolságra tolunk egy 20 N nagyságú vízszintes erővel. Mennyi munkát végzünk a dobozon? Ha a súrlódási erő 10 N, mennyi munkát végez a súrlódási erő? Mennyi a nettó munka?
2. Egy 2 kg tömegű labdát 3 m magasra emelünk. Mennyi munkát végezünk a labdán a gravitáció ellenében?
3. Egy rugót, amelynek rugóállandója 100 N/m, 0.2 m-rel megnyújtunk. Mennyi munkát végeztünk a rugó megnyújtása során?

6.2. Energia Feladatok

Munka Energia Teljesitmeny Fogalma

A Munka, Energia és Teljesítmény Fogalma: Átfogó Értelmezés

Ebben a részletes cikkben mélyrehatóan feltárjuk a fizika három alapvető fogalmát: a munkát, az energiát és a teljesítményt. Megvizsgáljuk azok definícióit, a közöttük lévő összefüggéseket, a mérésükre használt egységeket, valamint számos gyakorlati példán keresztül illusztráljuk a jelentőségüket a természettudományokban és a mindennapi életben. Célunk, hogy egy olyan átfogó képet nyújtsunk, amely nem csupán a fogalmak puszta ismertetésére szorítkozik, hanem azok mélyebb megértését is elősegíti.

A Munka Fizikai Értelmezése

A fizikában a munka fogalma eltér a mindennapi értelemben vett munkavégzéstől. Fizikai értelemben akkor végzünk munkát egy testtel, ha egy erő hatására az elmozdul. A munka tehát szorosan kapcsolódik mind az erőhöz, mind az elmozduláshoz. Ha egy erő hat egy testre, de az nem mozdul el, akkor fizikai értelemben nem beszélhetünk munkavégzésről.

A Munka Definíciója és Képlete

A munka (W) matematikailag az erő (\\mathbf\{F\}) és az elmozdulás (\\mathbf\{d\}) skaláris szorzataként definiálható:

\\mathbf\{W\} \= \\mathbf\{F\} \\cdot \\mathbf\{d\} \= \|\\mathbf\{F\}\| \|\\mathbf\{d\}\| \\cos \\theta

ahol:

• \|\\mathbf\{F\}\| az erő nagysága.
• \|\\mathbf\{d\}\| az elmozdulás nagysága.
• \\theta az erő és az elmozdulás vektorai közötti szög.

Ha az erő és az elmozdulás azonos irányú (\\theta \= 0^\\circ), akkor \\cos \\theta \= 1, és a végzett munka egyszerűen az erő és az elmozdulás szorzata: W \= Fd. Ha az erő és az elmozdulás egymásra merőleges (\\theta \= 90^\\circ), akkor \\cos \\theta \= 0, ami azt jelenti, hogy a végzett munka nulla. Például, ha egy súlyt vízszintesen tartunk, anélkül, hogy elmozdítanánk, akkor a gravitációs erő munkája nulla, mert az elmozdulás nulla.

A Munka Mértékegysége

A munka SI-mértékegysége a joule (J). Egy joule az a munka, amelyet akkor végzünk, ha egy newton (N) nagyságú erő egy méteren (m) keresztül hat egy testre az erő irányában. Tehát: 1 \\, \\text\{J\} \= 1 \\, \\text\{N\} \\cdot \\text\{m\}.

Pozitív és Negatív Munka

A végzett munka lehet pozitív, negatív vagy nulla. Pozitív munkát akkor végzünk, ha az erőnek az elmozdulás irányába eső komponense az elmozdulással azonos irányú. Ilyenkor az erő növeli a test mozgási energiáját. Negatív munkát akkor végzünk, ha az erőnek az elmozdulás irányába eső komponense az elmozdulással ellentétes irányú. Ilyenkor az erő csökkenti a test mozgási energiáját. A súrlódási erő például mindig negatív munkát végez, mert az elmozdulással ellentétes irányú.

Példák a Munkavégzésre

• Egy doboz felemelése a földről: A felfelé irányuló erő munkát végez a gravitációs erő ellenében. Ez pozitív munka.
• Egy autó fékezése: A fékrendszer által kifejtett súrlódási erő negatív munkát végez az autó mozgási energiáján.
• Egy bolygó keringése egy csillag körül: A gravitációs erő merőleges a bolygó sebességére, így nem végez munkát (ideális esetben, elhanyagolva a relativisztikus hatásokat és a többi égitest gravitációs hatását).

Az Energia Fogalma és Formái

Az energia egy test vagy rendszer munkavégző képessége. Számos formában létezhet, és az egyik formából a másikba alakulhat. Az energia megmaradási tétele az egyik legfontosabb alapelv a fizikában, amely kimondja, hogy egy zárt rendszer teljes energiája állandó marad, bár az energia formája megváltozhat.

A Kinetikus Energia

A kinetikus energia egy mozgó test energiája. Egy m tömegű, v sebességgel mozgó test kinetikus energiája (E\_k) a következőképpen számítható:

E\_k \= \\frac\{1\}\{2\}mv^2

A kinetikus energia mindig nemnegatív, és mértékegysége szintén a joule (J).

A Potenciális Energia

A potenciális energia egy test helyzetéből vagy konfigurációjából adódó energia. Többféle potenciális energia létezik, beleértve a gravitációs potenciális energiát, a rugalmas potenciális energiát és az elektromos potenciális energiát.

Gravitációs Potenciális Energia

A gravitációs potenciális energia egy m tömegű testnek a gravitációs mezőben elfoglalt helyzetéből adódó energiája. Ha a testet egy referencia szinthez képest h magasságban helyezzük el, akkor a gravitációs potenciális energiája (E\_p) a következő:

E\_p \= mgh

ahol g a gravitációs gyorsulás.

Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmasan deformált testben tárolt energia, például egy megnyújtott vagy összenyomott rugóban. Ha egy rugót x távolsággal nyújtunk meg vagy nyomunk össze a nyugalmi helyzetéből, akkor a benne tárolt rugalmas potenciális energia (E\_\{rug\}) a következő:

E\_\{rug\} \= \\frac\{1\}\{2\}kx^2

ahol k a rugóállandó.

A Belső Energia

A belső energia egy rendszer atomjainak és molekuláinak mozgásához és kölcsönhatásaihoz kapcsolódó energia. Magában foglalja a molekulák kinetikus energiáját (hőmozgás) és a potenciális energiáját (a molekulák közötti kötésekből adódóan). A belső energia megváltozása hőcsere vagy munkavégzés révén következhet be.

Egyéb Energiaformák

A fentieken kívül számos más energiaforma létezik, mint például:

• Hőenergia: A rendszer belső energiájának az a része, amely a hőmérsékletével arányos.
• Elektromos energia: Elektromos töltések mozgásához vagy elektromos mezőkhöz kapcsolódó energia.
• Mágneses energia: Mágneses mezőkhöz kapcsolódó energia.
• Kémiai energia: Az atomok és molekulák közötti kémiai kötésekben tárolt energia.
• Nukleáris energia: Az atommagban tárolt energia.
• Sugárzási energia: Elektromágneses hullámok formájában terjedő energia (pl. fény).

A Teljesítmény Fogalma

A teljesítmény (P) a munkavégzés sebességét vagy az energiaátalakulás sebességét adja meg. Azt mutatja meg, hogy mennyi munka végezhető el egységnyi idő alatt, vagy mennyi energia alakul át egységnyi idő alatt.

A Teljesítmény Definíciója és Képlete

A teljesítmény matematikailag a végzett munka (\\Delta W) és az eltelt idő (\\Delta t) hányadosaként definiálható:

P \= \\frac\{\\Delta W\}\{\\Delta t\}

Ha a teljesítmény állandó, akkor P \= W/t. A teljesítmény kifejezhető az erő és a sebesség segítségével is:

P \= \\mathbf\{F\} \\cdot \\mathbf\{v\} \= \|\\mathbf\{F\}\| \|\\mathbf\{v\}\| \\cos \\alpha

ahol \\mathbf\{v\} a sebesség, és \\alpha az erő és a sebesség vektorai közötti szög.

A Teljesítmény Mértékegysége

A teljesítmény SI-mértékegysége a watt (W). Egy watt az egy joule munka másodpercenként (1 \\, \\text\{W\} \= 1 \\, \\text\{J/s\}). Egy másik gyakran használt mértékegység a lóerő (LE), bár ez nem SI-egység (1 \\, \\text\{LE\} \\approx 746 \\, \\text\{W\}).

Példák a Teljesítményre

• Egy izzó teljesítménye megadja, hogy mennyi elektromos energiát alakít át fény- és hőenergiává másodpercenként.
• Egy motor teljesítménye azt mutatja meg, hogy milyen gyorsan képes munkát végezni (pl. egy jármű gyorsításakor).
• Egy erőmű teljesítménye azt jelzi, hogy mennyi elektromos energiát képes termelni másodpercenként.

A Munka, Energia és Teljesítmény Közötti Kapcsolat

A munka, az energia és a teljesítmény szorosan összefüggő fizikai mennyiségek. A munka az energiaátadás egyik formája. Ha egy rendszeren munkát végzünk, akkor az energiája megváltozik. Például, ha felemelünk egy tárgyat, munkát végzünk rajta, és ezzel növeljük a gravitációs potenciális energiáját. A teljesítmény pedig azt mutatja meg, hogy milyen gyorsan történik ez az energiaátadás vagy munkavégzés.

A Munkatétel

A munkatétel egy fontos összefüggés a munka és a kinetikus energia között. Kimondja, hogy egy testre ható összes erő által végzett eredő munka egyenlő a test kinetikus energiájának megváltozásával:

W\_\{eredő\} \= \\Delta E\_k \= E\_\{k,végső\} \- E\_\{k,kezdeti\} \= \\frac\{1\}\{2\}mv\_f^2 \- \\frac\{1\}\{2\}mv\_i^2

Ez a tétel rendkívül hasznos a mozgással kapcsolatos problémák megoldásában.

Az Energiamegmaradás Törvénye

Az energiamegmaradás törvénye az egyik legalapvetőbb természeti törvény. Kimondja, hogy egy zárt rendszer teljes energiája állandó marad. Az energia nem keletkezhet és nem semmisülhet meg, csak egyik formából a másikba alakulhat át. Például egy leeső tárgy gravitációs potenciális energiája fokozatosan kinetikus energiává alakul át.

Kapcsolat a Teljesítménnyel

Mint korábban említettük, a teljesítmény az energiaváltozás sebessége is:

P \= \\frac\{\\Delta E\}\{\\Delta t\}

Ez a képlet azt mutatja, hogy minél nagyobb a teljesítmény, annál gyorsabban történik az energiaátalakulás vagy a munkavégzés.

Gyakorlati Alkalmazások

A munka, az energia és a teljesítmény fogalmai alapvető fontosságúak a fizika számos területén és a mérnöki tudományokban. Néhány példa:

• Mechanika: A mozgás, erők és energia kölcsönhatásainak leírása.
• Termodinamika: A hő és a munka közötti kapcsolatok, valamint az energia átalakulásának tanulmányozása.
• Elektromosság és Magnetizmus: Az elektromos és mágneses mezőkben végzett munka és tárolt energia elemzése.

• Gépészet: Motorok, generátorok és más gépek tervezése és működésének megértése.
• Építészet: Az épületek energiahatékonyságának tervezése.
• Sport: A sportolók által kifejtett munka és teljesítmény elemzése.

Összefoglalás

Ebben a cikkben részletesen megvizsgáltuk a munka, az energia és a teljesítmény fogalmait. Láthattuk, hogy a munka egy erő által végzett energiaátadás, az energia a munkavégző képesség, a teljesítmény pedig a munkavégzés vagy energiaátalakulás sebessége. Megismertük a mérésükre használt egységeket és a közöttük lévő alapvető fizikai összefüggéseket, mint a munkatételt és az energiamegmaradás törvényét. Reméljük, hogy ez az átfogó magyarázat segített elmélyíteni ezen kulcsfontosságú fizikai fogalmak megértését.

Kulcsszavak összefoglalása:

• Munka: Erő hatására történő elmozdulással kapcsolatos energiaátadás.
• Energia: Munkavégző képesség, különböző formákban létezhet.
• Teljesítmény: A munkavégzés vagy energiaátalakulás sebessége.

A Munka Vektoros Jellege Részletesebben

Ahogy korábban említettük, a munka az erő és az elmozdulás skaláris szorzata. Ez azt jelenti, hogy a munka egy skaláris mennyiség, azaz csak nagysága van, iránya nincs. Azonban az erő és az elmozdulás vektorok, és a közöttük lévő szög (\\theta) kritikus a végzett munka szempontjából.

Esetek a Szög Függvényében

• Ha 0^\\circ \\le \\theta < 90^\\circ, akkor \\cos \\theta \> 0, és a munka pozitív. Ez azt jelenti, hogy az erőnek van az elmozdulás irányába eső komponense, ami hozzájárul a mozgáshoz vagy az energia növekedéséhez. Például egy lejtőn felfelé húzott tárgy esetén a húzóerő munkája pozitív.
• Ha \\theta \= 90^\\circ, akkor \\cos \\theta \= 0, és a munka nulla. Ez azt jelenti, hogy az erő merőleges az elmozdulásra, így nem végez munkát a mozgás irányában. Például egy vízszintes felületen egyenletes sebességgel mozgó testre ható függőleges tartóerő munkája nulla.
• Ha 90^\\circ < \\theta \\le 180^\\circ,

Munka Energia Teljesitmeny Fizika Tetel

A Munka, Energia és Teljesítmény Alapvető Tételei a Fizikában

A fizika egyik legfontosabb területe a mechanika, amely a testek mozgásával és az azokat kiváltó erőkkel foglalkozik. Ebben a kontextusban három alapvető fogalom kiemelkedő jelentőséggel bír: a munka, az energia és a teljesítmény. Ezek a fogalmak nem csupán elméleti konstrukciók, hanem a mindennapi életünk számos jelenségének megértéséhez és a technológiai fejlődéshez is nélkülözhetetlenek. Cikkünk célja, hogy részletesen feltárja ezen fogalmak lényegét, bemutassa a közöttük lévő összefüggéseket, és elmagyarázza a hozzájuk kapcsolódó alapvető fizikai tételeket.

1. A Munka Fogalma a Fizikában

A hétköznapi nyelvhasználattól eltérően a fizikában a munka egy pontosan definiált fogalom. Fizikai értelemben akkor végzünk munkát egy testtel, ha egy erő hatására a test elmozdul az erő irányában (vagy az erő elmozdulásának irányába eső komponense mentén). Matematikailag a munka (W) az erő (\\mathbf\{F\}) és az elmozdulás (\\mathbf\{d\}) skaláris szorzataként definiálható:

W \= \\mathbf\{F\} \\cdot \\mathbf\{d\} \= \|\\mathbf\{F\}\| \|\\mathbf\{d\}\| \\cos \\theta

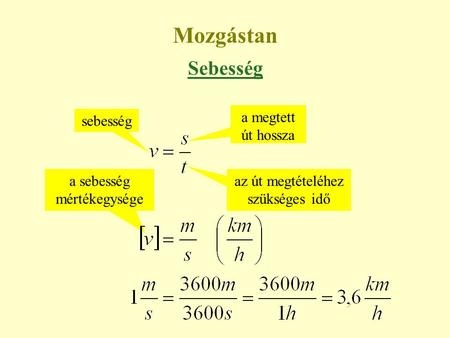
ahol \|\\mathbf\{F\}\| az erő nagysága, \|\\mathbf\{d\}\| az elmozdulás nagysága, \\theta pedig az erő és az elmozdulás közötti szög.

1.1. A Mechanikai Munka Különböző Esetei

Attól függően, hogy az erő és az elmozdulás milyen szögben áll egymáshoz, a végzett munka lehet pozitív, negatív vagy nulla:

• Pozitív munka: Ha az erőnek van az elmozdulás irányába eső komponense (0^\\circ \\le \\theta < 90^\\circ). Például, amikor egy dobozt húzunk a padlón, és az elmozdulás is ebben az irányban történik.
• Negatív munka: Ha az erőnek az elmozdulással ellentétes irányú komponense van (90^\\circ < \\theta \\le 180^\\circ). Például a súrlódási erő munkája, amikor egy test mozog, vagy amikor fékezünk egy autót.
• Nulla munka: Ha az erő merőleges az elmozdulásra (\\theta \= 90^\\circ), vagy ha az elmozdulás nulla. Például a gravitációs erő munkája egy vízszintes felületen egyenletesen mozgó testre nulla, vagy ha egy falat próbálunk tolni, de az nem mozdul el.

1.2. A Munka Mértékegysége

A munka SI-mértékegysége a joule (J). Egy joule az a munka, amelyet akkor végzünk, ha egy newton (N) nagyságú erő egy méteren (m) keresztül hat egy testre az erő irányában. Tehát: 1 \\, \\text\{J\} \= 1 \\, \\text\{N\} \\cdot \\text\{m\} \= 1 \\, \\text\{kg\} \\cdot \\text\{m\}^2/\\text\{s\}^2.

1.3. Változó Erő Munkája

Ha az erő nem állandó az elmozdulás során, akkor a munkát integrálással számíthatjuk ki. Egy egydimenziós mozgás esetén, ha az erő F\(x\) a pozíció függvénye, és a test x\_1-től x\_2-ig mozdul el, a végzett munka:

W \= \\int\_\{x\_1\}^\{x\_2\} F\(x\) \\, dx

Több dimenzióban ez az integrál vonalintegrállá alakul:

W \= \\int\_\{\\mathbf\{r\}\_1\}^\{\\mathbf\{r\}\_2\} \\mathbf\{F\} \\cdot d\\mathbf\{r\}

ahol d\\mathbf\{r\} az infinitezimális elmozdulásvektor.

2. Az Energia Fogalma a Fizikában

Az energia a fizikai rendszer azon képessége, hogy munkát végezzen. Számos formában létezhet, beleértve a kinetikus energiát (a mozgás energiája), a potenciális energiát (a helyzetből vagy konfigurációból származó energia), a hőenergiát, a kémiai energiát, a nukleáris energiát és a sugárzási energiát. Az energia SI-mértékegysége szintén a joule (J).

2.1. Kinetikus Energia

A kinetikus energia (K) egy mozgó test energiája. Egy m tömegű, v sebességgel mozgó test kinetikus energiája:

K \= \\frac\{1\}\{2\} m v^2

A kinetikus energia mindig nemnegatív, és a test sebességének négyzetével arányos.

2.2. Potenciális Energia

A potenciális energia (U) egy test helyzetéből vagy konfigurációjából származó tárolt energia. Különböző típusai léteznek, mint például a gravitációs potenciális energia és a rugalmas potenciális energia.

2.2.1. Gravitációs Potenciális Energia

A gravitációs potenciális energia egy m tömegű testnek a gravitációs mezőben elfoglalt helyzetéből adódik. A Föld felszínéhez közel, ahol a gravitációs gyorsulás (g) közel állandó, a h magasságban lévő test gravitációs potenciális energiája:

U\_g \= mgh

A potenciális energia nullpontjának megválasztása tetszőleges, de általában a Föld felszínét vagy egy referenciaszintet választunk.

2.2.2. Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmasan deformált testben (például egy megnyújtott vagy összenyomott rugóban) tárolt energia. Ha egy ideális rugót x távolsággal elmozdítunk egyensúlyi helyzetéből, a benne tárolt rugalmas potenciális energia:

U\_r \= \\frac\{1\}\{2\} k x^2

ahol k a rugóállandó, amely a rugó merevségét jellemzi.

3. A Munka–Energia Tétel

A munka–energia tétel egy alapvető elv a mechanikában, amely összekapcsolja a testre ható erők által végzett munkát a test kinetikus energiájának megváltozásával. A tétel kimondja, hogy egy testre ható összes erő által végzett eredő munka egyenlő a test kinetikus energiájának megváltozásával:

W\_\{eredő\} \= \\Delta K \= K\_f \- K\_i \= \\frac\{1\}\{2\} m v\_f^2 \- \\frac\{1\}\{2\} m v\_i^2

ahol v\_i a kezdeti sebesség és v\_f a végső sebesség.

3.1. Konzervatív Erők és Potenciális Energia

Bizonyos erők, mint például a gravitációs erő és a rugalmas erő, konzervatív erők. Egy konzervatív erő által végzett munka független az úttól, csak a kezdeti és a végső helyzettől függ. Konzervatív erők esetén bevezethető a potenciális energia fogalma úgy, hogy az erő által végzett munka egyenlő a potenciális energia negatív megváltozásával:

W\_c \= \-\\Delta U \= \-\(U\_f \- U\_i\) \= U\_i \- U\_f

ahol W\_c a konzervatív erő által végzett munka.

3.2. Nemkonzervatív Erők

Vannak olyan erők is, amelyek nem konzervatívak, például a súrlódási erő. A nemkonzervatív erők által végzett munka függ az úttól, és nem lehet hozzájuk potenciális energiát rendelni. A nemkonzervatív erők munkája (W\_\{nc\}) a rendszer mechanikai energiájának megváltozását okozza:

W\_\{nc\} \= \\Delta E\_\{mech\} \= \\Delta K \+ \\Delta U

ahol E\_\{mech\} \= K \+ U a mechanikai energia.

4. Az Energiamegmaradás Törvénye

Az energiamegmaradás törvénye az egyik legalapvetőbb elv a fizikában. Kimondja, hogy egy zárt rendszer teljes energiája állandó marad, feltéve, hogy nincsenek külső hatások. Az energia átalakulhat egyik formából a másikba, de nem keletkezhet és nem semmisülhet meg. Matematikailag:

\\Delta E\_\{total\} \= 0

ahol E\_\{total\} a rendszer összes energiájának összege.

4.1. Mechanikai Energia Megmaradása

Ha egy rendszerben csak konzervatív erők végeznek munkát, akkor a mechanikai energia megmarad:

\\Delta E\_\{mech\} \= \\Delta K \+ \\Delta U \= 0

K\_i \+ U\_i \= K\_f \+ U\_f

Ez azt jelenti, hogy a kezdeti mechanikai energia egyenlő a végső mechanikai energiával.

4.2. Általános Energiamegmaradás

Ha nemkonzervatív erők is jelen vannak, akkor a mechanikai energia nem marad meg, de a teljes energia (beleértve a hőenergiát stb.) igen. A nemkonzervatív erők által végzett munka a mechanikai energia egy részének más energiaformákká (például hővé) alakulását eredményezi.

5. A Teljesítmény Fogalma

A teljesítmény (P) a munka végzésének sebességét vagy az energiaátalakulás sebességét jelenti. Azt adja meg, hogy mennyi munka végezhető el egy adott idő alatt, vagy mennyi energia alakul át egységnyi idő alatt. Matematikailag:

P \= \\frac\{W\}\{\\Delta t\} \= \\frac\{dE\}\{dt\}

ahol W a végzett munka, \\Delta t az eltelt idő, dE az energiaváltozás, és dt az infinitezimális időintervallum.

5.1. Átlagos és Pillanatnyi Teljesítmény

• Átlagos teljesítmény (\\bar\{P\}): Az összes végzett munka osztva az eltelt idővel: \\bar\{P\} \= \\frac\{W\}\{\\Delta t\}.
• Pillanatnyi teljesítmény (P): A munka végzésének vagy energiaátalakulásnak a pillanatnyi sebessége: P \= \\lim\_\{\\Delta t \\to 0\} \\frac\{\\Delta W\}\{\\Delta t\} \= \\frac\{dW\}\{dt\}. Ha egy \\mathbf\{F\} erő hat egy \\mathbf\{v\} sebességgel mozgó testre, a pillanatnyi teljesítmény: P \= \\mathbf\{F\} \\cdot \\mathbf\{v\} \= \|\\mathbf\{F\}\| \|\\mathbf\{v\}\| \\cos \\phi, ahol \\phi az erő és a sebesség közötti szög.

5.2. A Teljesítmény Mértékegysége

A teljesítmény SI-mértékegysége a watt (W). Egy watt az egy joule munka másodpercenként (1 \\, \\text\{W\} \= 1 \\, \\text\{J/s\}). Egy másik gyakran használt mértékegység a lóerő (LE), bár ez nem SI-egység (1 \\, \\text\{LE\} \\approx 746 \\, \\text\{W\}).

6. Összefoglalás: A Munka, Energia és Teljesítmény Kapcsolata

A munka, az energia és a teljesítmény szorosan összefüggő fogalmak a fizikában. A munka az energiaátadás egyik formája. Amikor munka végeznek egy rendszeren, az energiája megváltozik. A teljesítmény pedig azt mutatja meg, hogy milyen gyorsan történik ez az energiaátadás vagy munkavégzés.

6.1. A Munka mint Energiaátadás

A munka tekinthető az energia egyik formájának, amelyet egy erő ad át egy testnek, miközben az elmozdul. Ha pozitív munka végeznek egy testen, az energiája nő (általában a kinetikus vagy potenciális energiája). Ha negatív munka végeznek, az energiája csökken.

6.2. Az Energia és a Teljesítmény Kapcsolata

A teljesítmény az időegységre eső energiaváltozás. Ha egy rendszerben \\Delta E energiaváltozás történik \\Delta t idő alatt, akkor az átlagos teljesítmény \\bar\{P\} \= \\frac\{\\Delta E\}\{\\Delta t\}. A pillanatnyi teljesítmény pedig a deriváltként adható meg: P \= \\frac\{dE\}\{dt\}.

7. Példák a Munka,

Munka Energia Teljesitmeny Feladatok Megoldassal

A Munka, Energia és Teljesítmény Világa: Átfogó Útmutató Feladatokkal és Részletes Megoldásokkal

Ebben a kimerítő cikkben mélyrehatóan feltárjuk a munka, az energia és a teljesítmény alapvető fogalmait a fizikában. Nem csupán definíciókkal szolgálunk, hanem részletes magyarázatokon keresztül vezetjük végig Olvasóinkat, illusztratív példákkal és gondosan kidolgozott feladatokkal segítve a megértést. Célunk, hogy Ön ne csak elsajátítsa ezeket a kulcsfontosságú fizikai elveket, hanem képes legyen azokat magabiztosan alkalmazni a legkülönfélébb problémák megoldása során.

A Munka Fogalma a Fizikában: Több, Mint Pusztán Fáradozás

A hétköznapi nyelvhasználattól eltérően a fizikában a munka egy precízen definiált fogalom. Akkor végzünk munkát egy testtel, ha egy erő hatására a test elmozdul az erő irányában (vagy az erő elmozdulás irányú komponense mentén). Matematikailag a munka (W) a testre ható erő (\\mathbf\{F\}) és az elmozdulás (\\mathbf\{d\}) skaláris szorzataként definiálható:

\\mathbf\{W\} \= \\mathbf\{F\} \\cdot \\mathbf\{d\} \= \|\\mathbf\{F\}\| \|\\mathbf\{d\}\| \\cos \\theta

ahol \|\\mathbf\{F\}\| az erő nagysága, \|\\mathbf\{d\}\| az elmozdulás nagysága, és \\theta az erő és az elmozdulás közötti szög. A munka mértékegysége a Joule (J), amely megegyezik az 1 Newton szorozva 1 méterrel (1 N⋅m).

Példa a Munka Számítására

Képzeljünk el egy esetet, ahol egy 10 N nagyságú vízszintes erővel eltolunk egy dobozt 5 méteren keresztül egy vízszintes felületen. Mivel az erő és az elmozdulás azonos irányú, a \\cos \\theta \= \\cos 0^\\circ \= 1. Így a végzett munka:

W \= \(10 \\, \\text\{N\}\) \\times \(5 \\, \\text\{m\}\) \\times 1 \= 50 \\, \\text\{J\}

Feladat 1: Munkavégzés Ferde Erővel

Egy 2 kg tömegű testet egy vízszintes felületen húzunk egy 20 N nagyságú erővel, amely a vízszintessel 30 fokos szöget zár be. Mekkora munkát végzünk, ha a test 3 métert mozdul el?

Megoldás:

Az erő vízszintes komponense F\_x \= \|\\mathbf\{F\}\| \\cos \\theta \= 20 \\, \\text\{N\} \\times \\cos 30^\\circ \= 20 \\, \\text\{N\} \\times \\frac\{\\sqrt\{3\}\}\{2\} \\approx 17\.32 \\, \\text\{N\}.

A végzett munka W \= F\_x \\times d \= 17\.32 \\, \\text\{N\} \\times 3 \\, \\text\{m\} \\approx 51\.96 \\, \\text\{J\}.

Az Energia Sokszínű Formái: A Munkavégzés Lehetősége

Az energia egy test vagy rendszer azon képessége, hogy munkát végezzen. Számos formában létezik, beleértve a kinetikus energiát (mozgás energiája), a potenciális energiát (helyzetből vagy állapotból származó energia), a termikus energiát (hő), a kémiai energiát, a nukleáris energiát és a sugárzási energiát. Az energia mértékegysége szintén a Joule (J).

Kinetikus Energia: A Mozgásban Rejlő Erő

Egy m tömegű, v sebességgel mozgó test kinetikus energiája (K) a következőképpen számítható:

K \= \\frac\{1\}\{2\} m v^2

Minél nagyobb a test tömege vagy sebessége, annál nagyobb a kinetikus energiája, és annál több munkát képes végezni a megállásáig.

Potenciális Energia: A Helyzetből Adódó Lehetőség

A potenciális energia egy test helyzetéből vagy konfigurációjából adódik. A leggyakrabban tárgyalt formái a gravitációs potenciális energia és a rugalmas potenciális energia.

Gravitációs Potenciális Energia

Egy m tömegű testnek a Föld felszínétől h magasságban lévő gravitációs potenciális energiája (U\_g) a következőképpen adható meg:

U\_g \= mgh

ahol g a gravitációs gyorsulás (kb. 9\.81 \\, \\text\{m/s\}^2 a Föld felszínén).

Rugalmas Potenciális Energia

Egy k rugóállandójú rugóban, amely x méterrel van megnyújtva vagy összenyomva, tárolt rugalmas potenciális energia (U\_e) a következőképpen számítható:

U\_e \= \\frac\{1\}\{2\} k x^2

Feladat 2: Kinetikus és Potenciális Energia

Egy 0.5 kg tömegű labdát 10 m/s sebességgel függőlegesen feldobunk a földről. Mekkora a labda kinetikus energiája a feldobás pillanatában? Mekkora a gravitációs potenciális energiája a legmagasabb ponton, ha a légellenállást elhanyagoljuk?

Megoldás:

A feldobás pillanatában a kinetikus energia: K \= \\frac\{1\}\{2\} \(0\.5 \\, \\text\{kg\}\) \(10 \\, \\text\{m/s\}\)^2 \= 25 \\, \\text\{J\}.

A legmagasabb ponton a kinetikus energia nulla (a labda pillanatnyi sebessége nulla). Az összes kezdeti kinetikus energia gravitációs potenciális energiává alakul. Így a legmagasabb ponton a potenciális energia is 25 J.

A Munkatétel: Kapocs a Munka és az Energia Között

A munkatétel egy alapvető elv a mechanikában, amely kimondja, hogy egy testre ható összes erő által végzett nettó munka egyenlő a test kinetikus energiájának megváltozásával:

W\_\{netto\} \= \\Delta K \= K\_f \- K\_i \= \\frac\{1\}\{2\} m v\_f^2 \- \\frac\{1\}\{2\} m v\_i^2

Ez a tétel rendkívül hasznos a mozgás elemzésében, különösen akkor, ha az erők nem állandóak.

Feladat 3: A Munkatétel Alkalmazása

Egy 1000 kg tömegű autó álló helyzetből indul, és egy állandó eredő erő hatására 20 m/s sebességet ér el 100 méter megtétele után. Mekkora volt az eredő erő?

Megoldás:

A kinetikus energia megváltozása: \\Delta K \= \\frac\{1\}\{2\} \(1000 \\, \\text\{kg\}\) \(20 \\, \\text\{m/s\}\)^2 \- \\frac\{1\}\{2\} \(1000 \\, \\text\{kg\}\) \(0 \\, \\text\{m/s\}\)^2 \= 200000 \\, \\text\{J\}.

A munkatétel szerint W\_\{netto\} \= \\Delta K, így F\_\{netto\} \\times d \= 200000 \\, \\text\{J\}.

Az eredő erő F\_\{netto\} \= \\frac\{200000 \\, \\text\{J\}\}\{100 \\, \\text\{m\}\} \= 2000 \\, \\text\{N\}.

Az Energia Megmaradásának Törvénye: Egyetemes Elv

Az energia megmaradásának törvénye az egyik legalapvetőbb és legszélesebb körben érvényesülő természeti törvény. Kimondja, hogy egy zárt rendszer teljes energiája állandó marad az időben. Az energia átalakulhat egyik formából a másikba, de nem keletkezhet és nem veszhet el.

Példa az Energia Megmaradására

Egy inga lengése során a gravitációs potenciális energia folyamatosan kinetikus energiává alakul, amikor az inga lefelé mozog, és fordítva, a kinetikus energia potenciális energiává alakul, amikor az inga felfelé lendül. Ha elhanyagoljuk a súrlódást és a légellenállást, a rendszer mechanikai energiája (a kinetikus és potenciális energia összege) állandó marad.

Feladat 4: Energia Megmaradás Inga Esetén

Egy 1 kg tömegű inga 1 méter hosszú fonálon lóg. Az ingát vízszintes helyzetből elengedjük. Mekkora lesz az inga sebessége a legalsó ponton?

Megoldás:

A kezdeti helyzetben az ingának csak gravitációs potenciális energiája van a legalsó ponthoz képest: U\_i \= mgh \= \(1 \\, \\text\{kg\}\) \(9\.81 \\, \\text\{m/s\}^2\) \(1 \\, \\text\{m\}\) \= 9\.81 \\, \\text\{J\}. A kezdeti kinetikus energia nulla.

A legalsó ponton a gravitációs potenciális energia nulla, és az összes kezdeti potenciális energia kinetikus energiává alakul: K\_f \= \\frac\{1\}\{2\} m v\_f^2.

Az energia megmaradásának törvénye szerint U\_i \= K\_f, így 9\.81 \\, \\text\{J\} \= \\frac\{1\}\{2\} \(1 \\, \\text\{kg\}\) v\_f^2.

Ebből a sebesség v\_f \= \\sqrt\{\\frac\{2 \\times 9\.81 \\, \\text\{J\}\}\{1 \\, \\text\{kg\}\}\} \\approx 4\.43 \\, \\text\{m/s\}.

A Teljesítmény Fogalma: A Munkavégzés Sebessége

A teljesítmény (P) azt adja meg, hogy milyen gyorsan végeznek munkát, vagy milyen gyorsan alakul át az energia. Matematikailag a teljesítmény a végzett munka és az eltelt idő hányadosa:

P \= \\frac\{W\}\{t\}

A teljesítményt az energia idő szerinti deriváltjaként is definiálhatjuk:

P \= \\frac\{dE\}\{dt\}

A teljesítmény mértékegysége a Watt (W), amely megegyezik az 1 Joule per másodperccel (1 J/s).

Teljesítmény Állandó Erő Esetén

Ha egy állandó \\mathbf\{F\} erő egy testet \\mathbf\{v\} sebességgel mozgat, akkor a teljesítmény:

P \= \\mathbf\{F\} \\cdot \\mathbf\{v\} \= \|\\mathbf\{F\}\| \|\\mathbf\{v\}\| \\cos \\phi

ahol \\phi az erő és a sebesség közötti szög.

Feladat 5: Teljesítmény Számítása

Egy daru egy 500 kg tömegű terhet 10 méter magasra emel fel 20 másodperc alatt állandó sebességgel. Mekkora a daru által kifejtett átlagos teljesítmény?

Megoldás:

A daru által végzett munka a gravitáció ellenében: W \= mgh \= \(500 \\, \\text\{kg\}\) \(9\.81 \\, \\text\{m/s\}^2\) \(10 \\, \\text\{m\}\) \= 49050 \\, \\text\{J\}.

Az átlagos teljesítmény: P \= \\frac\{W\}\{t\} \= \\frac\{49050 \\, \\text\{J\}\}\{20 \\, \\text\{s\}\} \= 2452\.5 \\, \\text\{W\}.

A Hatásfok: A Hasznos Munkavégzés Mértéke

A valóságban az energiaátalakítások sosem tökéletesek; mindig van valamennyi energiaveszteség, leggyakrabban hő formájában. A hatásfok (\\eta) azt adja meg, hogy egy rendszer a befektetett energiának vagy munkának mekkora hányadát képes hasznos munkává vagy energiává alakítani:

\\eta \= \\frac\{W\_\{hasznos\}\}\{W\_\{befektetett\}\} \= \\frac\{E\_\{hasznos\}\}\{E\_\{befektetett\}\}

A hatásfok mindig 0 és 1 (vagy 0% és 100%) közötti érték.

Példa a Hatásfokra

Egy elektromos motor 1000 J elektromos energiát vesz fel, és ennek hatására 800 J mechanikai munkát végez. A motor hatásfoka \\eta \= \\frac\{800 \\, \\text\{J\}\}\{1000 \\, \\text\{J\}\} \= 0\.8, vagyis 80%.

Feladat 6: Hatásfok Számítása

Egy benzinmotor 50000 J kémiai energiát alakít át, miközben 12500 J mechanikai munkát végez. Mekkora a motor hatásfoka?

Megoldás:

A motor hatásfoka: \\eta \= \\frac\{12500 \\, \\text\{J\}\}\{50000 \\, \\text\{J\}\} \= 0\.25, vagyis 25%.

További Összetett Feladatok a Munka, Energia és Teljesítmény Témakörében

Összetett Feladat 1: Lejtőn Csúszó Test

Egy 5 kg tömegű test egy 30