Energiamegmaradas Torvenye Ppt

Az Energia-megmaradás Törvénye: A Fizika Sarkköve

Az energia-megmaradás törvénye a fizika egyik legfontosabb és legalapvetőbb elve. Kimondja, hogy egy zárt rendszer teljes energiája időben állandó marad. Ez azt jelenti, hogy az energia nem keletkezhet a semmiből és nem veszhet el a semmibe, csupán egyik formájából átalakulhat egy másikba. Ez a megdöbbentően egyszerű, mégis mélyreható kijelentés áthatja a természettudományok szinte minden területét, a klasszikus mechanikától a termodinamikán át egészen a részecskefizikáig és a kozmológiáig. Cikkünkben részletesen feltárjuk ennek a fundamentális törvénynek a jelentőségét, történeti hátterét, különböző megnyilvánulásait és gyakorlati alkalmazásait.

Az Energia-megmaradás Történeti Gyökerei

Az energia-megmaradás gondolata nem egyetlen pillanatban született meg, hanem évszázadok tudományos munkájának és megfigyeléseinek eredményeként formálódott ki. Már a korai gondolkodók is felismerték bizonyos mennyiségek állandóságát a természeti jelenségekben. Például Arisztotelész a mozgás megmaradásával kapcsolatos elképzeléseket fogalmazott meg, bár ezek még nem voltak a modern értelemben vett energia-megmaradás koncepciójával egyenértékűek. A 17. században Christiaan Huygens tanulmányozta az ütközéseket, és megállapította, hogy bizonyos mennyiségek, mint például a mozgási energia egy speciális formája, megmaradnak rugalmas ütközések során.

A Mechanikai Munkától a Hő Természetéig

A 18. és 19. század fordulóján a mechanikai munka fogalmának pontosítása és a hő jelenségének megértése kulcsszerepet játszott az energia-megmaradás elvének megfogalmazásában. Benjamin Thompson (Rumford gróf) megfigyelései ágyúfúrás közben azt mutatták, hogy a súrlódás hatására korlátlan mennyiségű hő keletkezhet, ami megkérdőjelezte a hő korábban elfogadott, anyagszerű elméletét (a kalorikum-elméletet). Rumford kísérletei arra utaltak, hogy a hő valójában a mozgás egy formája.

A Termodinamika Első Főtételének Megszületése

A 19. század közepén olyan tudósok munkája nyomán, mint Julius Robert Mayer, James Prescott Joule és Hermann von Helmholtz, az energia-megmaradás elve egyre világosabbá és általánosabbá vált. Joule kísérletei, amelyekben mechanikai munkával hőt állított elő, és megmérte a kettő közötti ekvivalenciát (a mechanikai munka hőegyenértékét), döntő bizonyítékot szolgáltattak az energia különböző formái közötti átalakulásra és az energia összességének megmaradására. Helmholtz pedig 1847-ben megjelent munkájában, “Über die Erhaltung der Kraft” (Az erő megmaradásáról), átfogóan fogalmazta meg az energia-megmaradás általános elvét, amely magában foglalta a mechanikai, hő-, elektromos, mágneses és kémiai energiát is. Ez a munka tekinthető a termodinamika első főtételének egyik korai megfogalmazásának, amely kimondja, hogy egy zárt rendszer belső energiájának megváltozása egyenlő a rendszerrel közölt hő és a rendszeren végzett munka összegével: $$\Delta U = Q – W$$. Ebben az egyenletben $\Delta U$ a belső energia megváltozását, $Q$ a közölt hőt, $W$ pedig a rendszer által végzett munkát jelöli.

Az Energia Különböző Formái

Az energia a természet számos különböző formájában létezhet. Az energia-megmaradás törvénye azt állítja, hogy bár az energia formát válthat, a teljes mennyisége egy zárt rendszerben állandó marad. Nézzük meg az energia néhány fontosabb formáját:

Mechanikai Energia

A mechanikai energia egy objektum mozgásával és helyzetével kapcsolatos energia. Két fő összetevője van:

Mozgási Energia (Kinetikus Energia)

A mozgási energia egy test mozgásából származik. Egy $m$ tömegű, $v$ sebességgel mozgó test mozgási energiája a következőképpen számítható ki: $$E_k = \frac{1}{2}mv^2$$. Minél nagyobb a test tömege vagy sebessége, annál nagyobb a mozgási energiája. Például egy guruló labdának, egy repülő repülőgépnek vagy egy áramló víznek mozgási energiája van.

Potenciális Energia (Helyzeti Energia)

A potenciális energia egy test helyzetéből vagy konfigurációjából származik. Többféle potenciális energia létezik, attól függően, hogy milyen erőhatás hozza létre:

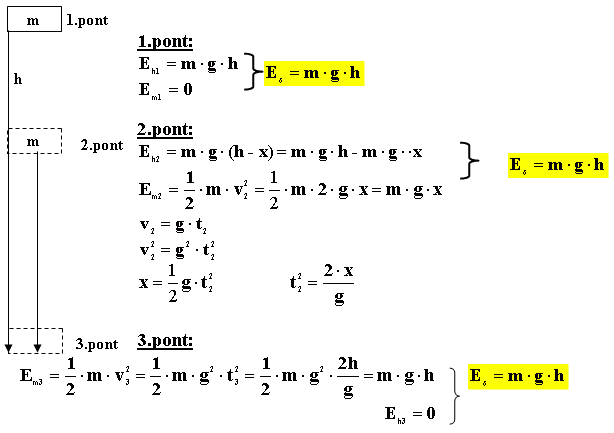
##### Gravitációs Potenciális Energia

A gravitációs potenciális energia egy test magasságától függ egy gravitációs mezőben. Egy $m$ tömegű, a referencia szinthez képest $h$ magasságban lévő test gravitációs potenciális energiája a Föld felszínén közelítőleg: $$E_p = mgh$$, ahol $g$ a gravitációs gyorsulás. Például egy felemelt kőnek vagy egy víztározóban lévő víznek gravitációs potenciális energiája van.

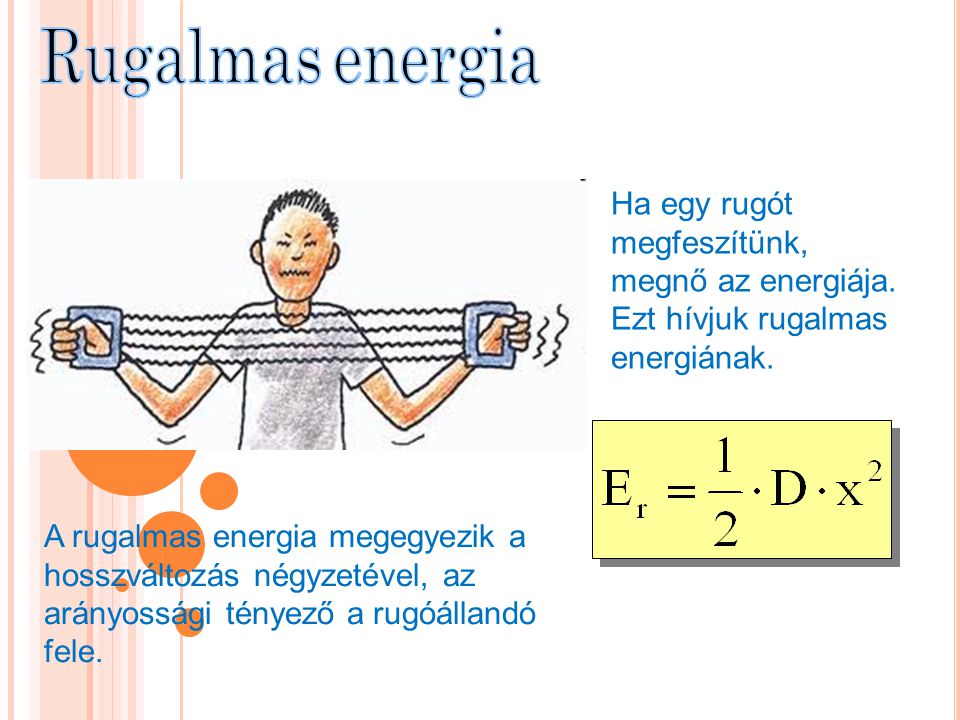
##### Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmas test (például egy rugó) deformációjából származik. Ha egy rugót $x$ távolsággal nyújtunk meg vagy nyomunk össze a nyugalmi helyzetéhez képest, akkor a benne tárolt rugalmas potenciális energia: $$E_{rug} = \frac{1}{2}kx^2$$, ahol $k$ a rugóállandó.

##### Elektromos Potenciális Energia

Az elektromos potenciális energia elektromos töltések kölcsönhatásából származik. Két $q_1$ és $q_2$ töltés közötti elektromos potenciális energia $r$ távolságban: $$E_{el} = k_e \frac{q_1 q_2}{r}$$, ahol $k_e$ a Coulomb-állandó.

##### Mágneses Potenciális Energia

A mágneses potenciális energia mágneses mezők kölcsönhatásából származik.

Hőenergia (Termikus Energia)

A hőenergia egy anyag atomjainak és molekuláinak véletlenszerű mozgásával kapcsolatos energia. Minél gyorsabban mozognak az atomok és molekulák, annál nagyobb az anyag hőenergiája, és annál magasabb a hőmérséklete. A hőenergia átadódhat egyik testről a másikra hő formájában (vezetés, áramlás, sugárzás).

Elektromágneses Energia

Az elektromágneses energia elektromos és mágneses mezőkhöz kapcsolódik. Az elektromágneses sugárzás, beleértve a látható fényt, a rádióhullámokat, a mikrohullámokat, az infravörös sugárzást, az ultraibolya sugárzást, a röntgensugarakat és a gammasugarakat, mind elektromágneses energiát hordoz. Ennek az energiának a terjedéséhez nincs szükség közegre.

Kémiai Energia

A kémiai energia az atomokat és molekulákat összetartó kémiai kötésekben tárolt energia. Kémiai reakciók során ezek a kötések felbomolhatnak vagy új kötések jöhetnek létre, ami energia felszabadulásával (exoterm reakciók) vagy energiaelnyeléssel (endoterm reakciók) járhat. Például a fa égésekor a kémiai energia hő- és fényenergiává alakul.

Nukleáris Energia

A nukleáris energia az atommagokban tárolt energia. Atommagreakciók, például a maghasadás (fisszió) vagy a magfúzió (fúzió) során hatalmas mennyiségű energia szabadulhat fel az atommagok átalakulása révén. Az atomerőművek a maghasadást használják fel elektromos energia előállítására, míg a Nap energiája a magfúzióból származik.

Az Energia-megmaradás Elvének Megnyilvánulásai

Az energia-megmaradás törvénye a természeti jelenségek széles körében megfigyelhető és alapvető szerepet játszik azok megértésében.

Mechanikai Rendszerekben

Egy ideális, súrlódásmentes mechanikai rendszerben a mozgási és potenciális energia összege állandó marad. Például egy inga lengése során a legmagasabb pontokon a potenciális energia maximális, a mozgási energia nulla, míg a legalacsonyabb ponton a mozgási energia maximális, a potenciális energia minimális (ha a referenciaszintet ott vesszük fel). A köztes pontokon az energia folyamatosan átalakul a két forma között, de az összegük állandó marad.

Termodinamikai Rendszerekben

A termodinamika első főtétele az energia-megmaradás elvének alkalmazása termodinamikai rendszerekre. Kimondja, hogy egy rendszer belső energiájának megváltozása egyenlő a rendszerrel közölt hő és a rendszeren végzett munka összegével. Ez azt jelenti, hogy az energia nem vész el és nem keletkezik, csak átalakulhat hővé vagy munkává, és megváltoztathatja a rendszer belső energiáját.

Elektromágneses Jelenségekben

Az elektromágneses mezők is energiát tárolnak. Például egy kondenzátor elektromos mezőben tárol energiát, míg egy induktor mágneses mezőben. Elektromágneses hullámok terjedésekor az elektromos és mágneses mezők energiája folyamatosan átalakul egymásba, de a hullám által szállított teljes energia megmarad.

Kémiai Reakciókban

Kémiai reakciók során az energia-megmaradás elve is érvényesül. Az exoterm reakciók során felszabaduló energia a kiindulási anyagok kémiai kötéseiben tárolt energia különbségéből származik, és ez az energia hő vagy fény formájában jelenik meg. Az endoterm reakciókhoz pedig energia befektetése szükséges a reakció végbemeneteléhez, ez az energia a környezetből vagy más energiaforrásból származik.

Nukleáris Reakciókban

A nukleáris reakciók, mint a maghasadás és a magfúzió, hatalmas energiakibocsátással járhatnak. Ebben az esetben az energia-megmaradás elve az energia és a tömeg ekvivalenciájának (amelyet Einstein híres $E=mc^2$ egyenlete fejez ki) kiterjesztésével értelmezhető. A reakció során a tömeg egy kis része energiává alakul, vagy fordítva, energia tömeggé alakulhat.

Példák az Energia-megmaradásra a Mindennapi Életben

Az energia-megmaradás törvénye nem csupán egy elméleti fogalom, hanem a mindennapi élet számos jelenségében megnyilvánul:

• Egy leejtett labda: Amikor a labdát elejtjük, a gravitációs potenciális energiája mozgási energiává alakul. A földnek ütközve ez az energia részben hővé és hanggá alakul, valamint deformálhatja a labdát és a talajt.
• Egy autó mozgása: Az autóban tárolt kémiai energia (az üzemanyagban) égés során hőenergiává alakul, amely aztán mechanikai munkává alakul a motorban, ami az autót mozgatja. A mozgás során fellépő súrlódás miatt a mechanikai energia egy része hővé alakul.
• Egy villanykörte világítása: Az elektromos energia a vezetékeken keresztül eljut a villanykörtébe, ahol fény- és hőenergiává alakul.
• Egy szélerőmű működése: A szél mozgási energiája forgatja a turbinákat, ami mechanikai energiát hoz létre, amelyet aztán egy generátor elektromos energiává alakít.
• A fotoszintézis: A növények a napfény elektromágneses energiáját használják fel szén-dioxidból és vízből glükóz (kémiai energia) előállítására.

Miért Fontos az Energia-megmaradás Törvénye?

Az energia-megmaradás törvénye rendkívül fontos a fizikában és más természettudományokban több okból is:

• Alapvető természeti törvény: Számos fizikai elmélet és számítás alapját képezi.
• Problémamegoldás: Segít bonyolult rendszerek viselkedésének megértésében és előrejelzésében. Az energia-megmaradás egyenletei gyakran egyszerűbbek a mozgásegyenleteknél, és elegendő információt nyújthatnak a rendszer végső állapotának meghatározásához.

• Lehetetlen folyamatok azonosítása: Lehetővé teszi olyan folyamatok azonosítását, amelyek ellentmondanak a fizika törvényeinek (például a perpetuum mobile első fajtája, amely külső energiaforrás nélkül végezne munkát).
• Technológiai fejlesztések: Számos technológiai alkalmazás alapul az energia különböző formáinak átalakításán, és az energia-megmaradás elvének megértése elengedhetetlen ezeknek a technológiáknak a tervezéséhez és optimalizálásához.

Az Energia-megmaradás és a Környezetvédelem

Az energia-megmaradás elvének megértése kulcsfontosságú a környezetvédelmi erőfeszítések szempontjából is. Bár az energia nem vész el, az átalakulások során gyakran olyan formák keletkeznek (például hő), amelyek kevésbé hasznosak vagy károsak a környezetre. Az energiahatékonyság növelése és a megújuló energiaforrások használata mind azon alapul, hogy minél hatékonyabban használjuk fel a rendelkezésre álló energiát és csökkentsük a nem kívánt energiaveszteségeket.

Mozgasi Energia Mertekegysege

A Mozgási Energia Mértékegysége: A Kinetikus Energia Részletes Feltárása

Ebben az átfogó cikkben részletesen megvizsgáljuk a mozgási energia mértékegységét, elmélyedünk a kinetikus energia fogalmában, annak fizikai jelentőségében, és bemutatjuk, hogyan számíthatjuk ki a mozgó testek energiáját. Célunk, hogy egy olyan kimerítő útmutatót nyújtsunk, amely minden kérdésre választ ad a témával kapcsolatban, legyen szó diákokról, tanárokról vagy a fizika iránt érdeklődőkről.

Mi az a Mozgási Energia (Kinetikus Energia)?

A mozgási energia, más néven kinetikus energia, az a munka, amely egy testet nyugalmi állapotból egy adott sebességre gyorsít fel. Képzeljünk el egy álló autót, amelyet eltolunk. Ahhoz, hogy az autó mozogni kezdjen, munkát kell végeznünk rajta, energiát kell befektetnünk. Ez a befektetett energia alakul át az autó mozgási energiájává. Minél nagyobb a test tömege és minél nagyobb a sebessége, annál nagyobb a mozgási energiája.

A Kinetikus Energia Fogalmának Mélyebb Értelmezése

A kinetikus energia nem más, mint a testek mozgásából származó energia. Ez egy skaláris mennyiség, ami azt jelenti, hogy csak nagysága van, iránya nincs. A kinetikus energia szorosan kapcsolódik a test impulzusához és a munkatételhez. A munkatétel kimondja, hogy egy testre ható összes erő által végzett munka egyenlő a test kinetikus energiájának megváltozásával.

Történelmi Áttekintés: A Mozgási Energia Koncepciójának Fejlődése

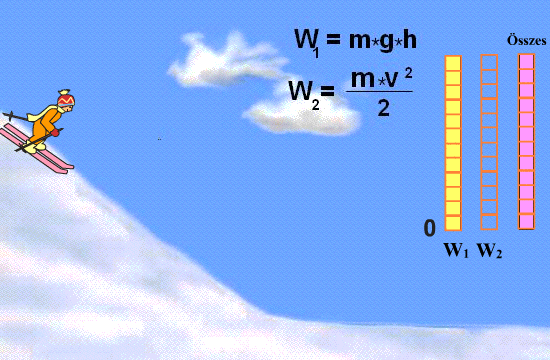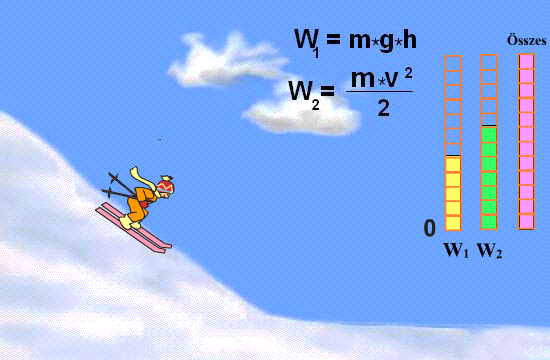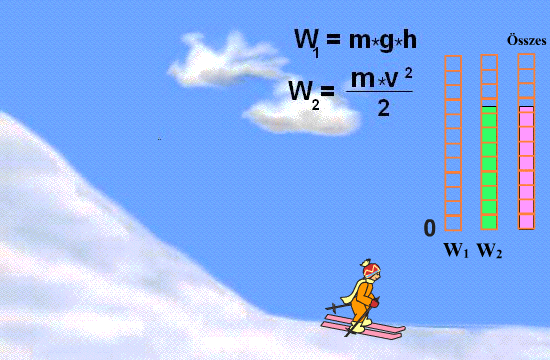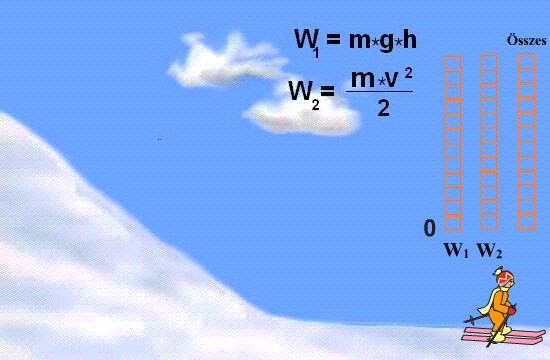
A mozgási energia fogalmának megértése évszázadokig tartó tudományos munka eredménye. Már a korai gondolkodók is felismerték a mozgás és az erő közötti kapcsolatot. A 17. században olyan tudósok, mint Galileo Galilei és Isaac Newton, lefektették a klasszikus mechanika alapjait, amelyek elengedhetetlenek a kinetikus energia pontos leírásához. A vis viva (élő erő) fogalma, amelyet Gottfried Wilhelm Leibniz és mások fejlesztettek ki, a kinetikus energia korai előfutárának tekinthető. A modern értelemben vett kinetikus energia fogalma a 19. században, a termodinamika és az energiamegmaradás törvényének kidolgozásával nyert végleges formát.

A Mozgási Energia Mértékegysége: A Joule

A mozgási energia (és általában mindenféle energia) nemzetközi mértékegységrendszerben (SI) mértékegysége a joule, amelyet James Prescott Joule angol fizikus tiszteletére neveztek el. A joule (J) egy származtatott SI-egység, amelyet az alapegységekkel a következőképpen fejezhetünk ki:

\\text\{1 J\} \= \\text\{1 kg\} \\cdot \\left\(\\frac\{\\text\{m\}\}\{\\text\{s\}\}\\right\)^2 \= \\text\{1 kg\} \\cdot \\text\{m\}^2 \\cdot \\text\{s\}^\{\-2\}

Ez azt jelenti, hogy egy joule az a munkamennyiség, amely ahhoz szükséges, hogy egy 1 kilogramm tömegű testet 1 méter per szekundum sebességre gyorsítsunk fel nyugalmi állapotból (bár ez nem a legközvetlenebb definíciója a joule-nak, de segít megérteni a kapcsolatot a tömeg, a sebesség és az energia között a kinetikus energia szempontjából). Pontosabban, egy joule az a munka, amelyet akkor végzünk, ha egy 1 newton nagyságú erőt 1 méter távolságon keresztül fejtünk ki az erő irányában.

A Joule Kapcsolata Más Mértékegységekkel

Fontos megérteni, hogy a joule nem csak a mozgási energia mértékegysége, hanem mindenféle energiáé, beleértve a potenciális energiát, a hőenergiát, a elektromágneses energiát stb. Gyakran találkozhatunk más energiamértékegységekkel is, mint például a kalória (cal) vagy a kilowattóra (kWh), de a tudományos és technikai területen az SI-rendszerbeli joule az elfogadott és preferált egység.

• 1 kalória (cal) ≈ 4,184 joule (J)
• 1 kilokalória (kcal) = 1000 kalória ≈ 4184 joule (J)
• 1 kilowattóra (kWh) = 3,6 × 10⁶ joule (J)

A Mozgási Energia Kiszámítása

A mozgási energia (E\_k) kiszámításának képlete rendkívül fontos a fizikában:

E\_k \= \\frac\{1\}\{2\} m v^2

Ahol:

• E\_k a mozgási energia (joule-ban)
• m a test tömege (kilogrammban)
• v a test sebessége (méter per szekundumban)

Ez az egyenlet azt mutatja, hogy a mozgási energia egyenesen arányos a test tömegével, és a sebesség négyzetével. Ez azt jelenti, hogy ha egy test sebessége kétszeresére nő, a mozgási energiája négyszeresére nő (ugyanazon tömeg mellett).

Példák a Mozgási Energia Számítására

1. Példa: Egy futó ember mozgási energiája

Egy 70 kg tömegű ember 5 m/s sebességgel fut. Számítsuk ki a mozgási energiáját!

E\_k \= \\frac\{1\}\{2\} \\cdot 70 \\text\{ kg\} \\cdot \(5 \\text\{ m/s\}\)^2 \= \\frac\{1\}\{2\} \\cdot 70 \\cdot 25 \\text\{ J\} \= 35 \\cdot 25 \\text\{ J\} \= 875 \\text\{ J\}

Tehát a futó ember mozgási energiája 875 joule.

2. Példa: Egy autó mozgási energiája

Egy 1000 kg tömegű autó 20 m/s sebességgel halad. Mekkora a mozgási energiája?

E\_k \= \\frac\{1\}\{2\} \\cdot 1000 \\text\{ kg\} \\cdot \(20 \\text\{ m/s\}\)^2 \= \\frac\{1\}\{2\} \\cdot 1000 \\cdot 400 \\text\{ J\} \= 500 \\cdot 400 \\text\{ J\} \= 200000 \\text\{ J\} \= 200 \\text\{ kJ\}

Az autó mozgási energiája 200 kilojoule.

3. Példa: Egy labda eldobása

Egy 0,5 kg tömegű labdát 10 m/s sebességgel eldobunk. Mennyi a labda mozgási energiája?

E\_k \= \\frac\{1\}\{2\} \\cdot 0,5 \\text\{ kg\} \\cdot \(10 \\text\{ m/s\}\)^2 \= \\frac\{1\}\{2\} \\cdot 0,5 \\cdot 100 \\text\{ J\} \= 0,25 \\cdot 100 \\text\{ J\} \= 25 \\text\{ J\}

A labda mozgási energiája 25 joule.

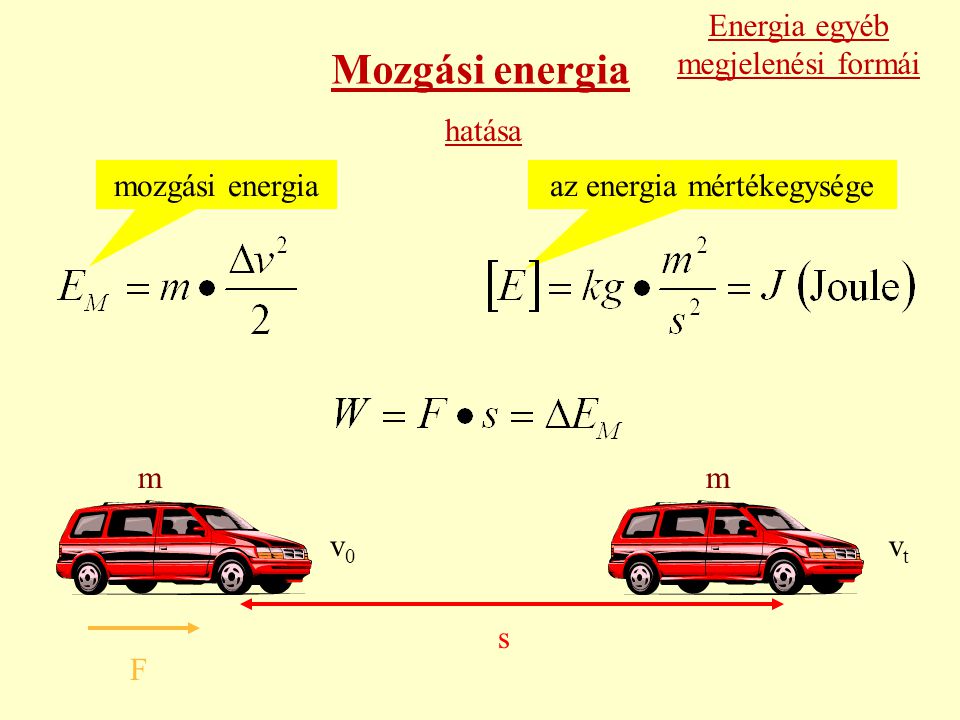
A Mozgási Energia és a Munka Kapcsolata

A munka-energia tétel alapvető fontosságú a fizika megértésében. Kimondja, hogy egy testre ható összes erő által végzett munka egyenlő a test kinetikus energiájának megváltozásával. Matematikailag:

W\_\{összes\} \= \\Delta E\_k \= E\_\{k,vég\} \- E\_\{k,kezdet\}

Ahol W\_\{összes\} a testre ható összes erő által végzett munka, \\Delta E\_k pedig a kinetikus energia megváltozása.

Példa a Munka-Energia Tételre

Egy álló 2 kg tömegű testre egy 10 N nagyságú, vízszintes erő hat 3 méteren keresztül. Mekkora lesz a test sebessége a 3 méter megtétele után?

1. A végzett munka kiszámítása: W \= F \\cdot d \= 10 \\text\{ N\} \\cdot 3 \\text\{ m\} \= 30 \\text\{ J\}.
2. A munka-energia tétel alkalmazása: W \= \\Delta E\_k \= E\_\{k,vég\} \- E\_\{k,kezdet\}. Mivel a test kezdetben nyugalomban volt, E\_\{k,kezdet\} \= 0. Tehát 30 \\text\{ J\} \= E\_\{k,vég\}.
3. A végső kinetikus energia képletének felhasználása a sebesség meghatározásához: E\_\{k,vég\} \= \\frac\{1\}\{2\} m v^2.

   30 \\text\{ J\} \= \\frac\{1\}\{2\} \\cdot 2 \\text\{ kg\} \\cdot v^2

   30 \= v^2

   v \= \\sqrt\{30\} \\text\{ m/s\} \\approx 5,48 \\text\{ m/s\}

   Tehát a test sebessége a 3 méter megtétele után körülbelül 5,48 m/s lesz.

A Mozgási Energia Különböző Formái és Kontextusai

A mozgási energia nem csak a lineáris mozgáshoz kapcsolódik. Megkülönböztethetünk más formáit is:

Rotációs Kinetikus Energia

A forgó testeknek is van mozgási energiájuk, amelyet rotációs kinetikus energiának nevezünk. Ez az energia a test tehetetlenségi nyomatékától (I) és szögsebességétől (\\omega) függ:

E\_\{rot\} \= \\frac\{1\}\{2\} I \\omega^2

Például egy forgó keréknek vagy egy pörgő korcsolyázónak van rotációs kinetikus energiája.

Rezgési Kinetikus Energia

A rezgő rendszerekben, mint például egy rugón lévő tömeg vagy egy hanghullám, az energia periodikusan alakul át potenciális és kinetikus energia között. A rezgési kinetikus energia a rezgő testek mozgásához kapcsolódik.

A Mozgási Energia Jelentősége a Különböző Területeken

A Közlekedésben

A közlekedési eszközök, mint az autók, vonatok, repülők, mind mozgási energiával rendelkeznek. A mozgási energia növeléséhez munkát kell végezni (pl. a motor által), a mozgási energia csökkentéséhez pedig fékezésre van szükség, amely során a mozgási energia más formákká (főként hővé) alakul át.

Az Ipari Termelésben

Számos ipari folyamat során a mozgási energia kulcsfontosságú. Gépek, szerszámok működnek mozgási energia segítségével, legyen szó forgó alkatrészekről, szállítószalagokról vagy megmunkáló eszközökről.

A Természetben

A természetben is mindenütt jelen van a mozgási energia. A szél mozgása (szélenergia), a víz áramlása (vízienergia), a hullámok mozgása (hullámenergia) mind a mozgási energia megnyilvánulásai. Az élőlények mozgása, a bolygók keringése a Nap körül szintén a mozgási energiához köthető.

A Mozgási Energia Megőrzése

Egy zárt rendszerben, ahol nincsenek disszipatív erők (mint például a súrlódás), a teljes mechanikai energia (a potenciális és a kinetikus energia összege) megmarad. Bár a kinetikus energia potenciális energiává alakulhat és fordítva, a kettő összege állandó marad. Ez az energiamegmaradás elve.

Példa az Energiamegmaradásra

Egy inga lengése során a legalsó ponton a potenciális energia a legkisebb (ha a nullszintet itt vesszük), és a kinetikus energia a legnagyobb. A legmagasabb pontokon pedig a kinetikus energia nulla (a pillanatnyi megállás miatt), és a potenciális energia a legnagyobb. A köztes pontokon az energia részben kinetikus, részben potenciális, de a kettő összege (ha nincsenek veszteségek) állandó.

Gyakran Ismételt Kérdések a Mozgási Energiával Kapcsolatban

Mi a különbség a mozgási energia és a potenciális energia között?

A mozgási energia egy test mozgásából származik, míg a potenciális energia a test helyzetéből vagy állapotából adódik (pl. gravitációs potenciális energia a magasságtól függ, rugalmas potenciális energia a rugó megnyúlásától).

Milyen tényezőktől függ a mozgási energia?

A mozgási energia két fő tényezőtől függ: a test tömegétől és a sebességének négyzetétől.

Lehet-e a mozgási energia negatív?

Nem, a mozgási energia mindig nemnegatív. A tömeg (m) mindig pozitív, és a sebesség négyzete (v^2) is mindig nemnegatív.

Mi a mozgási energia mértékegysége?

A mozgási energia mértékegysége a joule (J) a Nemzetközi Mértékegységrendszerben (SI).

Összefoglalás

A mozgási energia, vagy kinetikus energia, egy test mozgásának köszönhető energia. Mértékegysége a joule (J). Kiszámítása a E\_k \= \\frac\{1\}\{2\} m v^2 képlettel történik, ahol m a tömeg és v a sebesség. A mozgási energia alapvető fogalom a fizikában, és számos területen fontos szerepet játszik, a közlekedéstől a természeti jelenségekig. A munka-energia tétel és az energiamegmaradás elve segít megérteni a mozgási energia és más energiaformák közötti kapcsolatot.

További Olvasmányok és Források

• Fizika tankönyvek
• Online fizika kurzusok
• Tudományos cikkek a mechanikáról

Reméljük, hogy ez a részletes útmutató segített megérteni a mozg