Energiamegmaradas Torvenye Ppt

Az Energia-megmaradás Törvénye: A Fizika Sarkköve

Az energia-megmaradás törvénye a fizika egyik legfontosabb és legalapvetőbb elve. Kimondja, hogy egy zárt rendszer teljes energiája időben állandó marad. Ez azt jelenti, hogy az energia nem keletkezhet a semmiből és nem veszhet el a semmibe, csupán egyik formájából átalakulhat egy másikba. Ez a megdöbbentően egyszerű, mégis mélyreható kijelentés áthatja a természettudományok szinte minden területét, a klasszikus mechanikától a termodinamikán át egészen a részecskefizikáig és a kozmológiáig. Cikkünkben részletesen feltárjuk ennek a fundamentális törvénynek a jelentőségét, történeti hátterét, különböző megnyilvánulásait és gyakorlati alkalmazásait.

Az Energia-megmaradás Történeti Gyökerei

Az energia-megmaradás gondolata nem egyetlen pillanatban született meg, hanem évszázadok tudományos munkájának és megfigyeléseinek eredményeként formálódott ki. Már a korai gondolkodók is felismerték bizonyos mennyiségek állandóságát a természeti jelenségekben. Például Arisztotelész a mozgás megmaradásával kapcsolatos elképzeléseket fogalmazott meg, bár ezek még nem voltak a modern értelemben vett energia-megmaradás koncepciójával egyenértékűek. A 17. században Christiaan Huygens tanulmányozta az ütközéseket, és megállapította, hogy bizonyos mennyiségek, mint például a mozgási energia egy speciális formája, megmaradnak rugalmas ütközések során.

A Mechanikai Munkától a Hő Természetéig

A 18. és 19. század fordulóján a mechanikai munka fogalmának pontosítása és a hő jelenségének megértése kulcsszerepet játszott az energia-megmaradás elvének megfogalmazásában. Benjamin Thompson (Rumford gróf) megfigyelései ágyúfúrás közben azt mutatták, hogy a súrlódás hatására korlátlan mennyiségű hő keletkezhet, ami megkérdőjelezte a hő korábban elfogadott, anyagszerű elméletét (a kalorikum-elméletet). Rumford kísérletei arra utaltak, hogy a hő valójában a mozgás egy formája.

A Termodinamika Első Főtételének Megszületése

A 19. század közepén olyan tudósok munkája nyomán, mint Julius Robert Mayer, James Prescott Joule és Hermann von Helmholtz, az energia-megmaradás elve egyre világosabbá és általánosabbá vált. Joule kísérletei, amelyekben mechanikai munkával hőt állított elő, és megmérte a kettő közötti ekvivalenciát (a mechanikai munka hőegyenértékét), döntő bizonyítékot szolgáltattak az energia különböző formái közötti átalakulásra és az energia összességének megmaradására. Helmholtz pedig 1847-ben megjelent munkájában, “Über die Erhaltung der Kraft” (Az erő megmaradásáról), átfogóan fogalmazta meg az energia-megmaradás általános elvét, amely magában foglalta a mechanikai, hő-, elektromos, mágneses és kémiai energiát is. Ez a munka tekinthető a termodinamika első főtételének egyik korai megfogalmazásának, amely kimondja, hogy egy zárt rendszer belső energiájának megváltozása egyenlő a rendszerrel közölt hő és a rendszeren végzett munka összegével: $$\Delta U = Q – W$$. Ebben az egyenletben $\Delta U$ a belső energia megváltozását, $Q$ a közölt hőt, $W$ pedig a rendszer által végzett munkát jelöli.

Az Energia Különböző Formái

Az energia a természet számos különböző formájában létezhet. Az energia-megmaradás törvénye azt állítja, hogy bár az energia formát válthat, a teljes mennyisége egy zárt rendszerben állandó marad. Nézzük meg az energia néhány fontosabb formáját:

Mechanikai Energia

A mechanikai energia egy objektum mozgásával és helyzetével kapcsolatos energia. Két fő összetevője van:

Mozgási Energia (Kinetikus Energia)

A mozgási energia egy test mozgásából származik. Egy $m$ tömegű, $v$ sebességgel mozgó test mozgási energiája a következőképpen számítható ki: $$E_k = \frac{1}{2}mv^2$$. Minél nagyobb a test tömege vagy sebessége, annál nagyobb a mozgási energiája. Például egy guruló labdának, egy repülő repülőgépnek vagy egy áramló víznek mozgási energiája van.

Potenciális Energia (Helyzeti Energia)

A potenciális energia egy test helyzetéből vagy konfigurációjából származik. Többféle potenciális energia létezik, attól függően, hogy milyen erőhatás hozza létre:

##### Gravitációs Potenciális Energia

A gravitációs potenciális energia egy test magasságától függ egy gravitációs mezőben. Egy $m$ tömegű, a referencia szinthez képest $h$ magasságban lévő test gravitációs potenciális energiája a Föld felszínén közelítőleg: $$E_p = mgh$$, ahol $g$ a gravitációs gyorsulás. Például egy felemelt kőnek vagy egy víztározóban lévő víznek gravitációs potenciális energiája van.

##### Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmas test (például egy rugó) deformációjából származik. Ha egy rugót $x$ távolsággal nyújtunk meg vagy nyomunk össze a nyugalmi helyzetéhez képest, akkor a benne tárolt rugalmas potenciális energia: $$E_{rug} = \frac{1}{2}kx^2$$, ahol $k$ a rugóállandó.

##### Elektromos Potenciális Energia

Az elektromos potenciális energia elektromos töltések kölcsönhatásából származik. Két $q_1$ és $q_2$ töltés közötti elektromos potenciális energia $r$ távolságban: $$E_{el} = k_e \frac{q_1 q_2}{r}$$, ahol $k_e$ a Coulomb-állandó.

##### Mágneses Potenciális Energia

A mágneses potenciális energia mágneses mezők kölcsönhatásából származik.

Hőenergia (Termikus Energia)

A hőenergia egy anyag atomjainak és molekuláinak véletlenszerű mozgásával kapcsolatos energia. Minél gyorsabban mozognak az atomok és molekulák, annál nagyobb az anyag hőenergiája, és annál magasabb a hőmérséklete. A hőenergia átadódhat egyik testről a másikra hő formájában (vezetés, áramlás, sugárzás).

Elektromágneses Energia

Az elektromágneses energia elektromos és mágneses mezőkhöz kapcsolódik. Az elektromágneses sugárzás, beleértve a látható fényt, a rádióhullámokat, a mikrohullámokat, az infravörös sugárzást, az ultraibolya sugárzást, a röntgensugarakat és a gammasugarakat, mind elektromágneses energiát hordoz. Ennek az energiának a terjedéséhez nincs szükség közegre.

Kémiai Energia

A kémiai energia az atomokat és molekulákat összetartó kémiai kötésekben tárolt energia. Kémiai reakciók során ezek a kötések felbomolhatnak vagy új kötések jöhetnek létre, ami energia felszabadulásával (exoterm reakciók) vagy energiaelnyeléssel (endoterm reakciók) járhat. Például a fa égésekor a kémiai energia hő- és fényenergiává alakul.

Nukleáris Energia

A nukleáris energia az atommagokban tárolt energia. Atommagreakciók, például a maghasadás (fisszió) vagy a magfúzió (fúzió) során hatalmas mennyiségű energia szabadulhat fel az atommagok átalakulása révén. Az atomerőművek a maghasadást használják fel elektromos energia előállítására, míg a Nap energiája a magfúzióból származik.

Az Energia-megmaradás Elvének Megnyilvánulásai

Az energia-megmaradás törvénye a természeti jelenségek széles körében megfigyelhető és alapvető szerepet játszik azok megértésében.

Mechanikai Rendszerekben

Egy ideális, súrlódásmentes mechanikai rendszerben a mozgási és potenciális energia összege állandó marad. Például egy inga lengése során a legmagasabb pontokon a potenciális energia maximális, a mozgási energia nulla, míg a legalacsonyabb ponton a mozgási energia maximális, a potenciális energia minimális (ha a referenciaszintet ott vesszük fel). A köztes pontokon az energia folyamatosan átalakul a két forma között, de az összegük állandó marad.

Termodinamikai Rendszerekben

A termodinamika első főtétele az energia-megmaradás elvének alkalmazása termodinamikai rendszerekre. Kimondja, hogy egy rendszer belső energiájának megváltozása egyenlő a rendszerrel közölt hő és a rendszeren végzett munka összegével. Ez azt jelenti, hogy az energia nem vész el és nem keletkezik, csak átalakulhat hővé vagy munkává, és megváltoztathatja a rendszer belső energiáját.

Elektromágneses Jelenségekben

Az elektromágneses mezők is energiát tárolnak. Például egy kondenzátor elektromos mezőben tárol energiát, míg egy induktor mágneses mezőben. Elektromágneses hullámok terjedésekor az elektromos és mágneses mezők energiája folyamatosan átalakul egymásba, de a hullám által szállított teljes energia megmarad.

Kémiai Reakciókban

Kémiai reakciók során az energia-megmaradás elve is érvényesül. Az exoterm reakciók során felszabaduló energia a kiindulási anyagok kémiai kötéseiben tárolt energia különbségéből származik, és ez az energia hő vagy fény formájában jelenik meg. Az endoterm reakciókhoz pedig energia befektetése szükséges a reakció végbemeneteléhez, ez az energia a környezetből vagy más energiaforrásból származik.

Nukleáris Reakciókban

A nukleáris reakciók, mint a maghasadás és a magfúzió, hatalmas energiakibocsátással járhatnak. Ebben az esetben az energia-megmaradás elve az energia és a tömeg ekvivalenciájának (amelyet Einstein híres $E=mc^2$ egyenlete fejez ki) kiterjesztésével értelmezhető. A reakció során a tömeg egy kis része energiává alakul, vagy fordítva, energia tömeggé alakulhat.

Példák az Energia-megmaradásra a Mindennapi Életben

Az energia-megmaradás törvénye nem csupán egy elméleti fogalom, hanem a mindennapi élet számos jelenségében megnyilvánul:

• Egy leejtett labda: Amikor a labdát elejtjük, a gravitációs potenciális energiája mozgási energiává alakul. A földnek ütközve ez az energia részben hővé és hanggá alakul, valamint deformálhatja a labdát és a talajt.
• Egy autó mozgása: Az autóban tárolt kémiai energia (az üzemanyagban) égés során hőenergiává alakul, amely aztán mechanikai munkává alakul a motorban, ami az autót mozgatja. A mozgás során fellépő súrlódás miatt a mechanikai energia egy része hővé alakul.
• Egy villanykörte világítása: Az elektromos energia a vezetékeken keresztül eljut a villanykörtébe, ahol fény- és hőenergiává alakul.
• Egy szélerőmű működése: A szél mozgási energiája forgatja a turbinákat, ami mechanikai energiát hoz létre, amelyet aztán egy generátor elektromos energiává alakít.
• A fotoszintézis: A növények a napfény elektromágneses energiáját használják fel szén-dioxidból és vízből glükóz (kémiai energia) előállítására.

Miért Fontos az Energia-megmaradás Törvénye?

Az energia-megmaradás törvénye rendkívül fontos a fizikában és más természettudományokban több okból is:

• Alapvető természeti törvény: Számos fizikai elmélet és számítás alapját képezi.
• Problémamegoldás: Segít bonyolult rendszerek viselkedésének megértésében és előrejelzésében. Az energia-megmaradás egyenletei gyakran egyszerűbbek a mozgásegyenleteknél, és elegendő információt nyújthatnak a rendszer végső állapotának meghatározásához.

• Lehetetlen folyamatok azonosítása: Lehetővé teszi olyan folyamatok azonosítását, amelyek ellentmondanak a fizika törvényeinek (például a perpetuum mobile első fajtája, amely külső energiaforrás nélkül végezne munkát).
• Technológiai fejlesztések: Számos technológiai alkalmazás alapul az energia különböző formáinak átalakításán, és az energia-megmaradás elvének megértése elengedhetetlen ezeknek a technológiáknak a tervezéséhez és optimalizálásához.

Az Energia-megmaradás és a Környezetvédelem

Az energia-megmaradás elvének megértése kulcsfontosságú a környezetvédelmi erőfeszítések szempontjából is. Bár az energia nem vész el, az átalakulások során gyakran olyan formák keletkeznek (például hő), amelyek kevésbé hasznosak vagy károsak a környezetre. Az energiahatékonyság növelése és a megújuló energiaforrások használata mind azon alapul, hogy minél hatékonyabban használjuk fel a rendelkezésre álló energiát és csökkentsük a nem kívánt energiaveszteségeket.

Energiamegmaradas Torvenye Pelda

Az Energia-megmaradás Törvénye: A Világegyetem Alapvető Elve

Az energia-megmaradás törvénye a fizika egyik legfontosabb és legátfogóbb alapelve. Kimondja, hogy egy zárt rendszer teljes energiája időben állandó marad. Ez azt jelenti, hogy az energia nem teremthető és nem pusztítható el, csupán egyik formájából a másikba alakulhat át. Ez a látszólag egyszerű kijelentés mélyreható következményekkel jár a természeti jelenségek megértésére és a technológiai fejlesztésekre nézve. Cikkünkben részletesen feltárjuk az energia-megmaradás törvényének jelentését, különböző megjelenési formáit, és számos példán keresztül szemléltetjük alkalmazását a tudomány és a mindennapi élet különböző területein. Célunk, hogy egy átfogó és érthető képet nyújtsunk erről a fundamentális természeti törvényről, amely áthatja a minket körülvevő világ minden aspektusát.

Az Energia Fogalmának Meghatározása és Különböző Formái

Ahhoz, hogy megértsük az energia-megmaradás törvényét, először tisztáznunk kell magának az energia fogalmát. Az energia egy rendszer azon képessége, hogy munkát végezzen. Bár gyakran nehéz közvetlenül érzékelni, az energia jelenléte a különböző folyamatokban nyilvánvalóvá válik. Az energia számos különböző formában létezhet, amelyek mindegyike fontos szerepet játszik a természeti jelenségekben és a technológiai alkalmazásokban. Nézzük meg a legfontosabb energiaformákat:

Mechanikai Energia: Mozgás és Pozíció Potenciálja

A mechanikai energia egy test mozgásából (kinetikus energia) vagy a rá ható erőtérben elfoglalt helyzetéből (potenciális energia) származik. A kinetikus energia a mozgó testekkel kapcsolatos energia, amely a tömegüktől és a sebességük négyzeteivel arányos: $E_k = \frac{1}{2}mv^2$. Például egy guruló labdának, egy repülő repülőgépnek vagy egy forgó keréknek kinetikus energiája van. A potenciális energia egy test helyzetéből adódó energia egy erőterben. A leggyakoribb példa a gravitációs potenciális energia, amely egy test magasságától függ egy gravitációs mezőben: $E_p = mgh$, ahol $m$ a tömeg, $g$ a gravitációs gyorsulás, és $h$ a magasság egy referencia szinthez képest. Egy felemelt kőnek vagy egy megfeszített rugónak potenciális energiája van.

Hőenergia: A Részecskék Mozgásának Következménye

A hőenergia, más néven termikus energia, egy anyag atomjainak és molekuláinak véletlenszerű mozgásával kapcsolatos energia. Minél gyorsabban mozognak ezek a részecskék, annál nagyobb az anyag hőenergiája és annál magasabb a hőmérséklete. A hőenergia átadódhat egyik testről a másikra hő formájában, amelynek három fő módja van: hővezetés (kondukció), hőáramlás (konvekció) és hősugárzás (radiáció). A hőenergia alapvető szerepet játszik a termodinamikai folyamatokban és a mindennapi jelenségekben, mint például a víz forrása vagy a testünk melegen tartása.

Elektromágneses Energia: A Töltött Részecskék Kölcsönhatása

Az elektromágneses energia az elektromos és mágneses mezőkkel kapcsolatos energia. Ide tartozik a fény, a rádióhullámok, a mikrohullámok, az infravörös sugárzás, az ultraibolya sugárzás, a röntgensugarak és a gammasugarak. Ezek mind elektromágneses hullámok, amelyek energiát szállítanak. Az elektromos mezők töltött részecskék között hatnak, míg a mágneses mezők mozgó töltések (azaz áram) vagy mágneses dipólusok körül jönnek létre. Az elektromágneses energia nélkülözhetetlen a modern technológiában, az energiatermeléstől a kommunikációig.

Kémiai Energia: A Kötésekben Tárolt Potenciál

A kémiai energia az atomokat és molekulákat összetartó kémiai kötésekben tárolt potenciális energia. Ez az energia szabadul fel kémiai reakciók során, amikor a kötések átrendeződnek. Például a fa égésekor a fa molekuláiban tárolt kémiai energia hővé és fénnyé alakul át. Az élelmiszerekben tárolt kémiai energia pedig a szervezetünk számára biztosítja a működéshez szükséges energiát. A fosszilis tüzelőanyagok, mint a kőolaj, a földgáz és a szén, szintén jelentős mennyiségű kémiai energiát tárolnak.

Nukleáris Energia: Az Atommag Erejének Kiaknázása

A nukleáris energia az atommagban tárolt energia. Ez az energia felszabadulhat nukleáris reakciók során, mint például a maghasadás (fisszió), amikor egy nehéz atommag kisebb magokra bomlik, vagy a magfúzió (fúzió), amikor könnyű atommagok egyesülnek egy nehezebbé. A nukleáris energia hatalmas mennyiségű energiát képes felszabadítani, amit atomerőművekben villamos energia termelésére használnak, de atombombákban is alkalmaznak.

Az Energia-megmaradás Törvényének Formális Megfogalmazása

Az energia-megmaradás törvénye matematikailag is megfogalmazható. Egy zárt rendszerben a teljes energia ($E_{total}$) időben állandó:

$$\frac{dE_{total}}{dt} = 0$$

Ez azt jelenti, hogy ha egy rendszerben különböző energiaformák alakulnak át egymásba, a rendszer teljes energiája nem változik. Ha a rendszer nem zárt, azaz energia cserélődik a környezetével, akkor a rendszer energiájának megváltozása megegyezik a környezettel kicserélt energiával (munkavégzés vagy hőátadás formájában).

Történelmi Háttér: Az Energia-megmaradás Elvének Fejlődése

Az energia-megmaradás elvének felismerése egy hosszú és összetett folyamat volt a tudomány történetében. Számos tudós járult hozzá a koncepció kialakulásához különböző területeken végzett kísérleteikkel és elméleti munkájukkal.

A Korai Elképzelések és a Mechanikai Világnézet

A 17. és 18. században a tudósok, mint például Gottfried Wilhelm Leibniz, már felvetették a vis viva (élő erő) fogalmát, amely a mai kinetikus energiához hasonlít. Leibniz úgy vélte, hogy a vis viva megmarad a mechanikai kölcsönhatások során. Bár ez nem volt a teljes energia-megmaradás elve, fontos lépés volt a felé.

A Hő és a Munka Ekvivalenciájának Felfedezése

A 19. század elején olyan tudósok, mint Julius Robert Mayer, James Prescott Joule és Hermann von Helmholtz, kísérletekkel és elméleti megfontolásokkal kimutatták a hő és a munka közötti ekvivalenciát. Joule híres kísérleteivel bebizonyította, hogy a mechanikai munka hővé alakítható, és meghatározta a mechanikai munka és a hő egysége közötti átszámítási tényezőt (Joule-állandó). Mayer orvosi megfigyelései alapján jutott arra a következtetésre, hogy a hő és a munka különböző formái ugyanannak a dolognak, az energiának. Helmholtz pedig egy átfogó matematikai keretet adott az energia-megmaradás elvének.

Az Általános Elv Megszületése

Az 1840-es évekre az energia-megmaradás törvénye általánosan elfogadottá vált a tudományos közösségben, kiterjesztve a mechanikai, termikus, elektromos és kémiai jelenségekre is. Ez az elv alapvetővé vált a fizika és más természettudományok számára, és a mai napig is megkérdőjelezhetetlen érvényességgel bír.

Példák az Energia-megmaradás Törvényének Alkalmazására

Az energia-megmaradás törvénye számos természeti jelenség és technológiai alkalmazás megértésének kulcsa. Nézzünk meg néhány konkrét példát:

Mechanikai Rendszerek: A Hullámvasút Példája

Egy hullámvasút kocsija a pálya tetejére felhúzva potenciális energiával rendelkezik. Amikor a kocsi elindul lefelé, ez a potenciális energia fokozatosan kinetikus energiává alakul át, ami a kocsi sebességének növekedésében nyilvánul meg. A pálya alján a potenciális energia minimális, míg a kinetikus energia maximális. A felfelé ívelő szakaszokon a kinetikus energia ismét potenciális energiává alakul át. Ha nem lenne súrlódás és légellenállás, a kocsi folyamatosan ugyanarra a magasságra jutna vissza. A valóságban azonban a mechanikai energia egy része hővé alakul a súrlódás miatt, ezért a kocsi egyre alacsonyabbra jut a következő emelkedéseknél.

Termodinamikai Rendszerek: A Hőerőmű Működése

Egy hőerőműben valamilyen üzemanyag (például szén, földgáz vagy nukleáris anyag) elégetésével hőenergiát termelnek. Ez a hőenergia vizet forral fel, amely gőzt hoz létre. A nagynyomású gőz turbinákat hajt meg, amelyek mechanikai munkát végeznek. A turbinákhoz kapcsolt generátorok ezt a mechanikai munkát elektromos energiává alakítják át. Az energia-megmaradás törvénye itt abban nyilvánul meg, hogy az üzemanyagban tárolt kémiai vagy nukleáris energia végső soron elektromos energiává alakul át, miközben más energiaformák (például hőveszteség) is keletkeznek. A teljes energia mennyisége a folyamat során megmarad.

Elektromágneses Rendszerek: Az Elektromos Generátor

Egy elektromos generátor mechanikai energiát alakít át elektromos energiává. Például egy forgó mágnes egy tekercs közelében változó mágneses teret hoz létre, ami elektromos áramot indukál a tekercsben (Faraday-féle indukció). Az energia-megmaradás törvénye szerint a mechanikai munkával bevitt energia (a mágnes forgatása) az elektromos áram energiájává alakul át. A veszteségek (például a tekercs ellenállásából származó hő) szintén figyelembe veendők az energia-mérlegben.

Kémiai Reakciók: Az Égés Folyamata

A fa égése egy kémiai reakció, amely során a fa molekuláiban tárolt kémiai energia hővé és fénnyé alakul át. A reakció során a fa és az oxigén molekulái átrendeződnek, új molekulákat (például szén-dioxidot és vizet) hozva létre, miközben energia szabadul fel. Az energia-megmaradás törvénye itt azt jelenti, hogy a kiindulási anyagok kémiai energiájának és a felszabaduló hő- és fényenergiának az összege megegyezik a termékek kémiai energiájával (ami ebben az esetben alacsonyabb, mivel energia szabadult fel) plusz a környezetbe távozó bármilyen más energiával.

Nukleáris Reakciók: A Nap Működése

A Nap energiájának forrása a magfúzió, amelynek során a Nap magjában lévő hidrogénatomok héliumatomokká egyesülnek hatalmas hő és fény kibocsátása közben. Ebben a folyamatban a tömeg egy kis része energiává alakul át az $E=mc^2$ képlet szerint (Einstein híres egyenlete a tömeg és az energia ekvivalenciájáról). Bár a tömeg nem marad meg, a teljes energia (beleértve a tömegnek megfelelő energiát is) megmarad. A Nap által kibocsátott energia eljut a Földre, és alapvető fontosságú az élet fenntartásához.

Az Energia-megmaradás Törvényének Általánosítása

A relativitáselmélet megjelenésével Albert Einstein rámutatott a tömeg és az energia közötti szoros kapcsolatra. Az $E=mc^2$ egyenlet azt fejezi ki, hogy a tömeg is az energia egyik formája. Ezért a modern fizikában az energia-megmaradás törvényét gyakran a tömeg-energia megmaradásának törvényeként emlegetik, különösen a nukleáris fizikában és a nagy energiájú folyamatok leírásakor. Ebben az értelemben a zárt rendszer teljes tömeg-energiája marad állandó.

Következtetések: Az Energia-megmaradás Jelentősége

Az energia-megmaradás törvénye nem csupán egy fizikai elv, hanem egy alapvető keretrendszer, amely lehetővé teszi számunkra a természeti jelenségek megértését és a technológiai fejlesztéseket. Segítségével megérthetjük az erőművek működését, a járművek mozgását, a kémiai reakciók lejátszódását és a csillagok fényét. Bár az energia egyik formából a másikba átalakulhat, a teljes mennyisége mindig megmarad egy zárt rendszerben. Ez a törvény rávilágít az energia alapvető fontosságára és arra, hogy az energiaforrásaink végesek, ezért a hatékony energiafelhasználás és a fenntartható energiaforrások kutatása kiemelten fontos feladatunk.

További Vizsgálatok és Alkalmazások

Az energia-megmaradás törvénye továbbra is a modern fizika és mérnöki tudományok egyik sarokköve. Számos területen alkalmazz

Energiamegmaradas Elve

Az Energiamegmaradás Elve: A Természet Alapvető Törvénye

Az energiamegmaradás elve a fizika egyik legfontosabb és legalapvetőbb törvénye. Kimondja, hogy egy zárt rendszer teljes energiája időben állandó marad. Ez azt jelenti, hogy az energia nem keletkezhet a semmiből és nem veszhet el, csupán egyik formából a másikba alakulhat át. Ez az elv áthatja a természettudományok minden területét, a mechanikától a termodinamikán át az elektromágnességig és a részecskefizikáig. Megértése elengedhetetlen a természeti jelenségek helyes értelmezéséhez és a technológiai fejlesztésekhez.

Az Energiamegmaradás Elvének Formális Megfogalmazása

Formálisan az energiamegmaradás elvét a következőképpen fogalmazhatjuk meg: egy izolált rendszer teljes energiája állandó. Matematikailag ezt gyakran a következőképpen írjuk le:

$$\Delta E_{rendszer} = 0$$

Ahol $\Delta E_{rendszer}$ a rendszer teljes energiájának megváltozását jelöli. Ez azt jelenti, hogy ha a rendszer izolált (azaz nem cserél energiát a környezetével), akkor a benne lévő összes energia mennyisége nem változik meg. Az energia azonban átalakulhat különböző formák között, mint például kinetikus energia (mozgási energia), potenciális energia (helyzeti energia), hőenergia, elektromágneses energia, kémiai energia és nukleáris energia.

A Zárt és Izolált Rendszerek Fogalma

Fontos megkülönböztetni a zárt és az izolált rendszereket. Egy zárt rendszer olyan rendszer, amely nem cserél anyagot a környezetével, de energiát igen. Ezzel szemben egy izolált rendszer sem anyagot, sem energiát nem cserél a környezetével. Az energiamegmaradás elve szigorúan véve izolált rendszerekre vonatkozik. A valóságban tökéletesen izolált rendszerek nem léteznek, de sok esetben egy rendszer jó közelítéssel izoláltnak tekinthető egy adott időtartamra.

Példa zárt rendszerre

Egy lezárt edényben lévő gáz zárt rendszernek tekinthető, mert a gáz molekulái nem jutnak ki az edényből, de hő formájában energia cserélődhet az edény fala és a környezet között.

Példa (közelítőleg) izolált rendszerre

Egy jól szigetelt termoszban lévő forró kávé egy bizonyos ideig jó közelítéssel izolált rendszernek tekinthető, mivel mind az anyag (a kávé), mind az energia (hő) cseréje a környezettel minimális.

Az Energia Különböző Formái és Átalakulásuk

Az energia számos különböző formában létezhet, és ezek a formák egymásba alakulhatnak az energiamegmaradás elvének megfelelően.

Kinetikus Energia

A kinetikus energia egy test mozgásából származó energia. Egy $m$ tömegű, $v$ sebességgel mozgó test kinetikus energiája a következőképpen számítható:

$$E_k = \frac{1}{2}mv^2$$

Amikor egy tárgy sebessége megváltozik, a kinetikus energiája is megváltozik. Például, amikor egy autó gyorsul, a kinetikus energiája nő, mivel a sebessége nő. Ez az energia a motor által végzett munka révén kerül a rendszerbe, ami végső soron a benzin kémiai energiájából származik.

Potenciális Energia

A potenciális energia egy test helyzetéből vagy konfigurációjából származó tárolt energia. Többféle potenciális energia létezik:

Gravitációs potenciális energia

Egy $m$ tömegű, a Föld felszínétől $h$ magasságban lévő test gravitációs potenciális energiája a következőképpen számítható (feltételezve, hogy $h$ sokkal kisebb, mint a Föld sugara, és a gravitációs gyorsulás ($g$) állandó):

$$E_p = mgh$$

Amikor egy tárgy leesik, a gravitációs potenciális energiája kinetikus energiává alakul. Az energiamegmaradás elve ebben az esetben azt jelenti, hogy a kezdeti potenciális energia (a magasban) egyenlő a végső kinetikus energiával (a földet érés pillanatában), ha nem veszítünk energiát más formákban (pl. légellenállás).

Rugalmas potenciális energia

Egy megnyújtott vagy összenyomott rugó rugalmas potenciális energiával rendelkezik. Ha egy rugó $x$ távolsággal van kitérítve a nyugalmi helyzetéből, akkor a rugalmas potenciális energiája a következőképpen számítható (Hooke-törvényét feltételezve):

$$E_{rugalmas} = \frac{1}{2}kx^2$$

Ahol $k$ a rugóállandó. Amikor egy rugó elengedik, a rugalmas potenciális energia kinetikus energiává alakulhat, vagy munkát végezhet más testeken.

Hőenergia (Termikus Energia)

A hőenergia egy rendszer belső energiájának egy része, amely az atomok és molekulák véletlenszerű mozgásával kapcsolatos. Minél nagyobb a rendszer hőmérséklete, annál nagyobb az atomok és molekulák átlagos kinetikus energiája, és így annál nagyobb a hőenergiája. A hőenergia átadható egyik rendszerről a másikra hő formájában (vezetés, áramlás, sugárzás).

Elektromágneses Energia

Az elektromágneses energia az elektromos és mágneses mezőkkel kapcsolatos energia. Ide tartozik a fény, a rádióhullámok, a mikrohullámok, az infravörös és az ultraibolya sugárzás, a röntgensugárzás és a gammasugárzás. Ezek az energiák képesek terjedni a vákuumban is. Az elektromágneses energia kölcsönhatásba léphet a töltött részecskékkel, és energiát adhat át nekik.

Kémiai Energia

A kémiai energia az atomokat és molekulákat összetartó kémiai kötésekben tárolt energia. Kémiai reakciók során ezek a kötések felbomolhatnak vagy új kötések jöhetnek létre, ami energia felszabadulásával (exoterm reakció) vagy energiafelvétellel (endoterm reakció) járhat. Például az égés során a kémiai energia hő- és fényenergiává alakul.

Nukleáris Energia

A nukleáris energia az atommagban tárolt energia, amely az atommagot alkotó nukleonok (protonok és neutronok) közötti erős kölcsönhatásból származik. Nukleáris reakciók, mint például a maghasadás (fisszió) vagy a magfúzió (fúzió), hatalmas mennyiségű nukleáris energiát szabadíthatnak fel.

Az Energiamegmaradás Elvének Alkalmazásai

Az energiamegmaradás elvének számos fontos alkalmazása van a tudományban és a mérnöki gyakorlatban.

Mechanika

A mechanikában az energiamegmaradás elve segít megérteni a mozgást és a kölcsönhatásokat. Például egy inga mozgása során a gravitációs potenciális energia folyamatosan kinetikus energiává alakul és fordítva, miközben a teljes mechanikai energia (a kinetikus és a potenciális energia összege) állandó marad (ideális esetben, súrlódás nélkül).

Példa: Az egyszerű inga

Egy $m$ tömegű, $L$ hosszúságú fonálon függő inga kezdetben $\theta$ szögben van kitérítve. Amikor elengedjük, a gravitációs potenciális energiája csökken, miközben a kinetikus energiája nő. A legalacsonyabb ponton a potenciális energia minimális, a kinetikus energia pedig maximális. Az energiamegmaradás elve alapján:

$$mgh_{kezdeti} = \frac{1}{2}mv_{legalsó}^2$$

Ahol $h_{kezdeti} = L(1 – \cos\theta)$ a kezdeti magasság, és $v_{legalsó}$ a legalacsonyabb ponton lévő sebesség.

Termodinamika

A termodinamika első főtétele az energiamegmaradás elvének egy speciális megfogalmazása termodinamikai rendszerekre. Kimondja, hogy egy zárt rendszer belső energiájának ($\Delta U$) megváltozása egyenlő a rendszerrel közölt hő ($Q$) és a rendszeren végzett munka ($W$) összegével:

$$\Delta U = Q – W$$

Ez az egyenlet azt fejezi ki, hogy az energia nem vész el és nem keletkezik, csak átalakulhat hővé vagy munkává, és megváltoztathatja a rendszer belső energiáját.

Példa: Gáz expanziója

Ha egy gáz egy hengerben expandál, munkát végez a dugattyún. Ha közben hőt adunk a gázhoz, akkor a belső energiája is megváltozhat. A termodinamika első főtétele segít számszerűsíteni ezeket az energiaátalakulásokat.

Elektromágnesség

Az elektromágnességben az energiamegmaradás elve megnyilvánul például az elektromágneses mező energiájában. Egy elektromos mező és egy mágneses mező energiát tárolhat, és ez az energia átalakulhat más formákká, például a töltött részecskék mozgási energiájává vagy hővé (Joule-hő).

Példa: Kondenzátor kisülése

Egy feltöltött kondenzátor elektromos energiát tárol az elektromos mezőjében. Amikor egy ellenálláson keresztül kisül, ez az energia hővé alakul az ellenállásban (Joule-effektus). Az energiamegmaradás elve azt mondja ki, hogy a kondenzátor kezdeti elektromos energiája egyenlő az ellenálláson disszipált hőenergiával.

Relativitáselmélet és az Energia-Tömeg Ekvivalencia

Einstein speciális relativitáselmélete egy mély kapcsolatot tárt fel az energia és a tömeg között. Az híres $E=mc^2$ egyenlet kimondja, hogy az energia ($E$) és a tömeg ($m$) ekvivalensek egymással, ahol $c$ a fény sebessége vákuumban. Ez azt jelenti, hogy a tömeg az energia egy formája, és az energia tömeggé alakulhat, és fordítva. A relativisztikus energiamegmaradás elve szerint egy zárt rendszer teljes relativisztikus energiája (amely magában foglalja a nyugalmi energiát $mc^2$-t is) megmarad.

Példa: Atomreakciók

Az atomreakciókban, mint például a maghasadás vagy a magfúzió, a tömeg egy kis része energiává alakul át az $E=mc^2$ egyenlet szerint, ami hatalmas mennyiségű energia felszabadulásához vezet.

Az Energiamegmaradás Elvének Kísérleti Bizonyítékai

Az energiamegmaradás elvét számtalan kísérlet és megfigyelés támasztja alá a fizika, a kémia és más természettudományok területén. Soha nem találtak olyan jelenséget, amely egyértelműen megszegné ezt az elvet. Ezért tekintjük az egyik legszilárdabb és legáltalánosabb természeti törvénynek.

A Joule-kísérlet

James Prescott Joule híres kísérletei a 19. század közepén fontos bizonyítékot szolgáltattak a mechanikai munka és a hő közötti ekvivalenciára, ami az energiamegmaradás elvének egyik korai megerősítése volt. Joule megmutatta, hogy egy adott mennyiségű mechanikai munka mindig ugyanannyi hőt termel, függetlenül attól, hogyan végezzük a munkát.

Elektromágneses indukció

Faraday elektromágneses indukciós kísérletei megmutatták, hogy a változó mágneses mező elektromos mezőt hoz létre, és fordítva. Ezek a jelenségek az elektromágneses energia átalakulását és megmaradását tükrözik.

Atom- és magfizikai kísérletek

Az atom- és magfizikai kísérletek során végzett precíz mérések is megerősítették az energiamegmaradás elvét, beleértve a relativisztikus formáját is. Az elemi részecskék kölcsönhatásai és az atommagok átalakulásai során a teljes energia (beleértve a tömegenergiát is) mindig megmarad.

Az Energiamegmaradás Elvének Filozófiai Jelentősége

Az energiamegmaradás elvének nem csak tudományos, hanem filozófiai jelentősége is van. Azt sugallja, hogy a világban van valami állandó és megőrződő, még akkor is, ha minden látszólag változik. Ez az elv hozzájárul a természet egységének és koherenciájának megértéséhez.

A megmaradási törvények szerepe a fizikában

Az energiamegmaradás elve csak egy a sok megmaradási törvény közül a fizikában. Hasonlóan fontos a lendületmegmaradás, a tömegmegmaradás (klasszikus fizikában), a töltésmegmaradás és más megmaradási törvények. Ezek a törvények alapvető szimmetriákkal állnak kapcsolatban a tér, az idő és más fizikai mennyiségek tekintetében (Noether-tétel).

Összefoglalás

Az energiamegmaradás elve a természet egyik legmélyebb és legáltalánosabb törvénye. Kimondja, hogy egy izolált rendszer teljes energiája állandó. Az energia különböző formákban létezhet (kinetikus, potenciális, hő, elektromágneses, kémiai, nukleáris), és ezek a formák egymásba alakulhat

Munka Energia Teljesitmeny Hatasfok Feladatok

A Munka, Energia, Teljesítmény és Hatásfok Mélyreható Tanulmányozása

Ebben a részletes cikkben átfogóan vizsgáljuk a fizika négy alapvető fogalmát: a munkát, az energiát, a teljesítményt és a hatásfokot. Célunk, hogy ne csupán definíciókat adjunk, hanem mélyrehatóan megértsük ezen fogalmak közötti összefüggéseket, gyakorlati alkalmazásaikat és a hozzájuk kapcsolódó számítási módszereket. Számos példán és kidolgozott feladaton keresztül segítjük az olvasót a téma alapos elsajátításában.

1. A Munka Fogalma a Fizikában

A fizikában a munka akkor végezhető, ha egy erő egy testet elmozdít. Fontos megjegyezni, hogy pusztán egy erő hatása nem feltétlenül jelent munkavégzést; az elmozdulás elengedhetetlen. Matematikailag a munka (W) egy állandó \\mathbf\{F\} erő által végzett munkát, amely egy testet egyenes vonalban \\mathbf\{d\} vektorral elmozdít, a következőképpen definiáljuk:

\\mathbf\{W\} \= \\mathbf\{F\} \\cdot \\mathbf\{d\} \= \|\\mathbf\{F\}\| \|\\mathbf\{d\}\| \\cos \\theta

ahol \|\\mathbf\{F\}\| az erő nagysága, \|\\mathbf\{d\}\| az elmozdulás nagysága, és \\theta az erő és az elmozdulás vektorai közötti szög. A munka SI mértékegysége a joule (J), amely megegyezik egy newton méterrel (N·m).

1.1. Pozitív, Negatív és Nulla Munka

A végzett munka lehet pozitív, negatív vagy nulla, attól függően, hogy az erő és az elmozdulás vektorai milyen szöget zárnak be egymással.

• Pozitív munka: Ha az erőnek az elmozdulás irányába eső komponense van (\\theta < 90^\\circ), a munka pozitív. Például, amikor egy izom összehúzódik és megemel egy súlyt, az izom által kifejtett erő pozitív munkát végez a súlyon.
• Negatív munka: Ha az erőnek az elmozdulással ellentétes irányú komponense van (90^\\circ < \\theta \\le 180^\\circ), a munka negatív. Például, amikor egy súlyt lassan leengedünk, a gravitációs erő negatív munkát végez a súlyon (az elmozdulás felfelé, a gravitációs erő lefelé irányul). A súrlódási erő is negatív munkát végez, mivel mindig a mozgással ellentétes irányú.
• Nulla munka: Ha az erő merőleges az elmozdulásra (\\theta \= 90^\\circ), vagy ha nincs elmozdulás (\|\\mathbf\{d\}\| \= 0), a munka nulla. Például, egy vízszintes felületen egyenletes sebességgel haladó testre ható függőleges tartóerő nem végez munkát, mert az erő merőleges az elmozdulásra. Továbbá, ha valaki egy nehéz tárgyat tart a helyén anélkül, hogy elmozdulna, nem végez munkát a tárgyon, annak ellenére, hogy erőt fejt ki.

1.2. Változó Erő Munkája

Ha az erő nem állandó, vagy az elmozdulás nem egyenes vonalú, a végzett munkát integrálással számíthatjuk ki. Egy egydimenziós esetben, ha egy F\(x\) erő hat egy testre, miközben az x\_1 pozícióból az x\_2 pozícióba mozdul el, a végzett munka:

W \= \\int\_\{x\_1\}^\{x\_2\} F\(x\) \\, dx

Három dimenzióban ez az integrál egy görbe mentén történik:

W \= \\int\_\{\\mathbf\{r\}\_1\}^\{\\mathbf\{r\}\_2\} \\mathbf\{F\} \\cdot d\\mathbf\{r\}

ahol d\\mathbf\{r\} az infiniteszimális elmozdulásvektor a pálya mentén.

1.3. Példák a Munkavégzésre

• Egy ember egy nehéz dobozt tol a padlón. A tolóerő munkát végez a dobozon, ha az elmozdul. A súrlódási erő negatív munkát végez.
• Egy lift felemel egy személyt. A lift kábelének húzóereje pozitív munkát végez a személyen. A gravitációs erő negatív munkát végez.
• Egy műhold kering a Föld körül. A gravitációs erő (ami ebben az esetben centripetális erő) nem végez munkát a műholdon, mert az erő mindig merőleges a sebességre (és így az infiniteszimális elmozdulásra).

2. Az Energia Fogalma és Formái

Az energia egy rendszer azon képessége, hogy munkát végezzen. Skalár mennyiség, és SI mértékegysége szintén a joule (J). Az energia számos formában létezhet, és az egyik formából a másikba alakulhat át. A munkatétel alapvető fontosságú az energia és a munka közötti kapcsolat megértéséhez. Kimondja, hogy egy testre ható összes erő által végzett munka egyenlő a test kinetikus energiájának megváltozásával:

W\_\{összes\} \= \\Delta K \= K\_f \- K\_i \= \\frac\{1\}\{2\}mv\_f^2 \- \\frac\{1\}\{2\}mv\_i^2

ahol m a test tömege, v\_i a kezdeti sebesség és v\_f a végső sebesség.

2.1. Kinetikus Energia

A kinetikus energia (K) egy mozgó test energiája, amely a tömegétől (m) és a sebességének a négyzetétől (v) függ:

K \= \\frac\{1\}\{2\}mv^2

Minél nagyobb egy test tömege vagy sebessége, annál nagyobb a kinetikus energiája.

2.2. Potenciális Energia

A potenciális energia egy test helyzetéből vagy konfigurációjából adódó tárolt energia. Különböző típusai léteznek:

• Gravitációs potenciális energia (U\_g): Egy m tömegű test gravitációs potenciális energiája a Föld felszínéhez képest h magasságban:

  U\_g \= mgh

  ahol g a gravitációs gyorsulás.

• Rugalmas potenciális energia (U\_e): Egy k rugóállandójú rugóban tárolt energia, ha x távolsággal megnyújtjuk vagy összenyomjuk a nyugalmi helyzetéhez képest:

  U\_e \= \\frac\{1\}\{2\}kx^2

• Elektromos potenciális energia: Elektromos töltések közötti kölcsönhatásból származó energia.
• Kémiai potenciális energia: Az atomok és molekulák közötti kémiai kötésekben tárolt energia.
• Nukleáris potenciális energia: Az atommagban tárolt energia.

2.3. Az Energia Megmaradásának Törvénye

Az egyik legfontosabb természeti törvény az energia megmaradásának törvénye, amely kimondja, hogy egy zárt rendszer teljes energiája állandó marad, bár az energia egyik formából a másikba alakulhat át. Matematikailag:

E\_\{kezdeti\} \= E\_\{végső\}

Például, egy leeső labda gravitációs potenciális energiája fokozatosan kinetikus energiává alakul át (a légellenállást elhanyagolva). A teljes mechanikai energia (E \= K \+ U) állandó marad.

3. A Teljesítmény Definíciója és Jelentősége

A teljesítmény (P) a munka végzésének sebességét vagy az energiaátalakulás sebességét adja meg. Más szóval, megmutatja, hogy milyen gyorsan végeznek munkát vagy alakítanak át energiát. Matematikailag:

P \= \\frac\{W\}\{t\} \= \\frac\{dE\}\{dt\}

ahol W a végzett munka, t az idő, E az energia és t az idő. A teljesítmény SI mértékegysége a watt (W), amely megegyezik egy joule per szekundummal (J/s).

3.1. Átlagos és Pillanatnyi Teljesítmény

• Átlagos teljesítmény: Az összes végzett munka osztva az eltelt idővel:

  P\_\{átlagos\} \= \\frac\{\\Delta W\}\{\\Delta t\}

• Pillanatnyi teljesítmény: A teljesítmény egy adott pillanatban, ami a munka idő szerinti deriváltja:

  P \= \\lim\_\{\\Delta t \\to 0\} \\frac\{\\Delta W\}\{\\Delta t\} \= \\frac\{dW\}\{dt\}

  Ha egy \\mathbf\{F\} erő hat egy testre, amely \\mathbf\{v\} sebességgel mozog, a pillanatnyi teljesítmény kifejezhető a következőképpen is:

  

  P \= \\mathbf\{F\} \\cdot \\mathbf\{v\} \= \|\\mathbf\{F\}\| \|\\mathbf\{v\}\| \\cos \\phi

  ahol \\phi az erő és a sebesség vektorai közötti szög.

3.2. A Teljesítmény Gyakorlati Alkalmazásai

A teljesítmény fogalma kulcsfontosságú számos területen, például a gépészetben (motorok teljesítménye), az elektromosságban (elektromos eszközök fogyasztása) és a biológiában (izomzat által kifejtett teljesítmény).

• Egy autó motorjának teljesítménye megmutatja, hogy milyen gyorsan képes munkát végezni a jármű gyorsításához vagy emelkedőn való feljutáshoz.
• Egy izzó teljesítménye (wattban megadva) azt jelzi, hogy másodpercenként mennyi elektromos energiát alakít át fény- és hőenergiává.

4. A Hatásfok Fogalma és Számítása

A hatásfok (\\eta) egy rendszer vagy folyamat hatékonyságának mértéke. Azt adja meg, hogy a befektetett energia vagy végzett munka mekkora része hasznos munkává vagy a kívánt energiaformává alakul át. A hatásfok egy dimenzió nélküli mennyiség, amelyet gyakran százalékban adnak meg. Matematikailag:

\\eta \= \\frac\{\\text\{Hasznos kimenet\}\}\{\\text\{Befektetett bemenet\}\} \= \\frac\{W\_\{hasznos\}\}\{W\_\{befektetett\}\} \= \\frac\{E\_\{hasznos\}\}\{E\_\{befektetett\}\} \= \\frac\{P\_\{hasznos\}\}\{P\_\{befektetett\}\}

Mivel a kimenet sosem lehet nagyobb a bemenetnél (az energiamegmaradás törvénye miatt), a hatásfok mindig kisebb vagy egyenlő 1-gyel (vagy 100%-kal).

4.1. Példák a Hatásfokra

• Egy villanymotor hatásfoka megmutatja, hogy a felvett elektromos energia mekkora hányada alakul át mechanikai munkává. A maradék energia általában hő formájában veszik el.
• Egy hőerőgép hatásfoka azt jelzi, hogy a befektetett hőenergia mekkora része alakul át mechanikai munkává. A Carnot-ciklus adja meg a hőerőgépek elméleti maximális hatásfokát.
• Egy napelem hatásfoka azt mutatja meg, hogy a beeső napfény energiájának mekkora hányadát alakítja át elektromos energiává.

4.2. A Hatásfok Növelésének Fontossága

A hatásfok növelése számos szempontból fontos. Gazdasági szempontból kevesebb bemeneti energiára van szükség ugyanazon hasznos kimenet eléréséhez, ami költségmegtakarítást eredményez. Környezetvédelmi szempontból a magasabb hatásfok kevesebb energiafelhasználást jelent, ami csökkenti a természeti erőforrások kimerülését és a környezetszennyezést.

5. Kapcsolat a Munka, Energia, Teljesítmény és Hatásfok Között

Ezek a négy fogalom szorosan összefügg egymással. A munka az energiaátadás egyik formája. Az energia a munkavégzés képessége. A teljesítmény a munka végzésének vagy az energiaátalakulás sebessége. A hatásfok pedig azt méri, hogy ez az energiaátalakulás mennyire hatékony.

Gyakran egy rendszerbe energiát fektetünk be, amely munkát végez. A teljesítmény megadja, hogy ez a munkavégzés milyen gyorsan történik, a hatásfok pedig azt, hogy a befektetett energia mekkora része fordítódik hasznos munkára.

6. Gyakorlati Feladatok a Munka, Energia, Teljesítmény és Hatásfok Témakörében

Az alábbiakban néhány gyakorlati feladatot talál, amelyek segítenek elmélyíteni a fent tárgyalt fogalmak megértését.

6.1. Munka Feladatok

1. Egy 50 kg tömegű dobozt vízszintes felületen 10 m távolságra tolunk egy 20 N nagyságú vízszintes erővel. Mennyi munkát végzünk a dobozon? Ha a súrlódási erő 10 N, mennyi munkát végez a súrlódási erő? Mennyi a nettó munka?
2. Egy 2 kg tömegű labdát 3 m magasra emelünk. Mennyi munkát végezünk a labdán a gravitáció ellenében?
3. Egy rugót, amelynek rugóállandója 100 N/m, 0.2 m-rel megnyújtunk. Mennyi munkát végeztünk a rugó megnyújtása során?

6.2. Energia Feladatok

Munka Energia Teljesitmeny Feladatok Megoldassal

A Munka, Energia és Teljesítmény Világa: Átfogó Útmutató Feladatokkal és Részletes Megoldásokkal

Ebben a kimerítő cikkben mélyrehatóan feltárjuk a munka, az energia és a teljesítmény alapvető fogalmait a fizikában. Nem csupán definíciókkal szolgálunk, hanem részletes magyarázatokon keresztül vezetjük végig Olvasóinkat, illusztratív példákkal és gondosan kidolgozott feladatokkal segítve a megértést. Célunk, hogy Ön ne csak elsajátítsa ezeket a kulcsfontosságú fizikai elveket, hanem képes legyen azokat magabiztosan alkalmazni a legkülönfélébb problémák megoldása során.

A Munka Fogalma a Fizikában: Több, Mint Pusztán Fáradozás

A hétköznapi nyelvhasználattól eltérően a fizikában a munka egy precízen definiált fogalom. Akkor végzünk munkát egy testtel, ha egy erő hatására a test elmozdul az erő irányában (vagy az erő elmozdulás irányú komponense mentén). Matematikailag a munka (W) a testre ható erő (\\mathbf\{F\}) és az elmozdulás (\\mathbf\{d\}) skaláris szorzataként definiálható:

\\mathbf\{W\} \= \\mathbf\{F\} \\cdot \\mathbf\{d\} \= \|\\mathbf\{F\}\| \|\\mathbf\{d\}\| \\cos \\theta

ahol \|\\mathbf\{F\}\| az erő nagysága, \|\\mathbf\{d\}\| az elmozdulás nagysága, és \\theta az erő és az elmozdulás közötti szög. A munka mértékegysége a Joule (J), amely megegyezik az 1 Newton szorozva 1 méterrel (1 N⋅m).

Példa a Munka Számítására

Képzeljünk el egy esetet, ahol egy 10 N nagyságú vízszintes erővel eltolunk egy dobozt 5 méteren keresztül egy vízszintes felületen. Mivel az erő és az elmozdulás azonos irányú, a \\cos \\theta \= \\cos 0^\\circ \= 1. Így a végzett munka:

W \= \(10 \\, \\text\{N\}\) \\times \(5 \\, \\text\{m\}\) \\times 1 \= 50 \\, \\text\{J\}

Feladat 1: Munkavégzés Ferde Erővel

Egy 2 kg tömegű testet egy vízszintes felületen húzunk egy 20 N nagyságú erővel, amely a vízszintessel 30 fokos szöget zár be. Mekkora munkát végzünk, ha a test 3 métert mozdul el?

Megoldás:

Az erő vízszintes komponense F\_x \= \|\\mathbf\{F\}\| \\cos \\theta \= 20 \\, \\text\{N\} \\times \\cos 30^\\circ \= 20 \\, \\text\{N\} \\times \\frac\{\\sqrt\{3\}\}\{2\} \\approx 17\.32 \\, \\text\{N\}.

A végzett munka W \= F\_x \\times d \= 17\.32 \\, \\text\{N\} \\times 3 \\, \\text\{m\} \\approx 51\.96 \\, \\text\{J\}.

Az Energia Sokszínű Formái: A Munkavégzés Lehetősége

Az energia egy test vagy rendszer azon képessége, hogy munkát végezzen. Számos formában létezik, beleértve a kinetikus energiát (mozgás energiája), a potenciális energiát (helyzetből vagy állapotból származó energia), a termikus energiát (hő), a kémiai energiát, a nukleáris energiát és a sugárzási energiát. Az energia mértékegysége szintén a Joule (J).

Kinetikus Energia: A Mozgásban Rejlő Erő

Egy m tömegű, v sebességgel mozgó test kinetikus energiája (K) a következőképpen számítható:

K \= \\frac\{1\}\{2\} m v^2

Minél nagyobb a test tömege vagy sebessége, annál nagyobb a kinetikus energiája, és annál több munkát képes végezni a megállásáig.

Potenciális Energia: A Helyzetből Adódó Lehetőség

A potenciális energia egy test helyzetéből vagy konfigurációjából adódik. A leggyakrabban tárgyalt formái a gravitációs potenciális energia és a rugalmas potenciális energia.

Gravitációs Potenciális Energia

Egy m tömegű testnek a Föld felszínétől h magasságban lévő gravitációs potenciális energiája (U\_g) a következőképpen adható meg:

U\_g \= mgh

ahol g a gravitációs gyorsulás (kb. 9\.81 \\, \\text\{m/s\}^2 a Föld felszínén).

Rugalmas Potenciális Energia

Egy k rugóállandójú rugóban, amely x méterrel van megnyújtva vagy összenyomva, tárolt rugalmas potenciális energia (U\_e) a következőképpen számítható:

U\_e \= \\frac\{1\}\{2\} k x^2

Feladat 2: Kinetikus és Potenciális Energia

Egy 0.5 kg tömegű labdát 10 m/s sebességgel függőlegesen feldobunk a földről. Mekkora a labda kinetikus energiája a feldobás pillanatában? Mekkora a gravitációs potenciális energiája a legmagasabb ponton, ha a légellenállást elhanyagoljuk?

Megoldás:

A feldobás pillanatában a kinetikus energia: K \= \\frac\{1\}\{2\} \(0\.5 \\, \\text\{kg\}\) \(10 \\, \\text\{m/s\}\)^2 \= 25 \\, \\text\{J\}.

A legmagasabb ponton a kinetikus energia nulla (a labda pillanatnyi sebessége nulla). Az összes kezdeti kinetikus energia gravitációs potenciális energiává alakul. Így a legmagasabb ponton a potenciális energia is 25 J.

A Munkatétel: Kapocs a Munka és az Energia Között

A munkatétel egy alapvető elv a mechanikában, amely kimondja, hogy egy testre ható összes erő által végzett nettó munka egyenlő a test kinetikus energiájának megváltozásával:

W\_\{netto\} \= \\Delta K \= K\_f \- K\_i \= \\frac\{1\}\{2\} m v\_f^2 \- \\frac\{1\}\{2\} m v\_i^2

Ez a tétel rendkívül hasznos a mozgás elemzésében, különösen akkor, ha az erők nem állandóak.

Feladat 3: A Munkatétel Alkalmazása

Egy 1000 kg tömegű autó álló helyzetből indul, és egy állandó eredő erő hatására 20 m/s sebességet ér el 100 méter megtétele után. Mekkora volt az eredő erő?

Megoldás:

A kinetikus energia megváltozása: \\Delta K \= \\frac\{1\}\{2\} \(1000 \\, \\text\{kg\}\) \(20 \\, \\text\{m/s\}\)^2 \- \\frac\{1\}\{2\} \(1000 \\, \\text\{kg\}\) \(0 \\, \\text\{m/s\}\)^2 \= 200000 \\, \\text\{J\}.

A munkatétel szerint W\_\{netto\} \= \\Delta K, így F\_\{netto\} \\times d \= 200000 \\, \\text\{J\}.

Az eredő erő F\_\{netto\} \= \\frac\{200000 \\, \\text\{J\}\}\{100 \\, \\text\{m\}\} \= 2000 \\, \\text\{N\}.

Az Energia Megmaradásának Törvénye: Egyetemes Elv

Az energia megmaradásának törvénye az egyik legalapvetőbb és legszélesebb körben érvényesülő természeti törvény. Kimondja, hogy egy zárt rendszer teljes energiája állandó marad az időben. Az energia átalakulhat egyik formából a másikba, de nem keletkezhet és nem veszhet el.

Példa az Energia Megmaradására

Egy inga lengése során a gravitációs potenciális energia folyamatosan kinetikus energiává alakul, amikor az inga lefelé mozog, és fordítva, a kinetikus energia potenciális energiává alakul, amikor az inga felfelé lendül. Ha elhanyagoljuk a súrlódást és a légellenállást, a rendszer mechanikai energiája (a kinetikus és potenciális energia összege) állandó marad.

Feladat 4: Energia Megmaradás Inga Esetén

Egy 1 kg tömegű inga 1 méter hosszú fonálon lóg. Az ingát vízszintes helyzetből elengedjük. Mekkora lesz az inga sebessége a legalsó ponton?

Megoldás:

A kezdeti helyzetben az ingának csak gravitációs potenciális energiája van a legalsó ponthoz képest: U\_i \= mgh \= \(1 \\, \\text\{kg\}\) \(9\.81 \\, \\text\{m/s\}^2\) \(1 \\, \\text\{m\}\) \= 9\.81 \\, \\text\{J\}. A kezdeti kinetikus energia nulla.

A legalsó ponton a gravitációs potenciális energia nulla, és az összes kezdeti potenciális energia kinetikus energiává alakul: K\_f \= \\frac\{1\}\{2\} m v\_f^2.

Az energia megmaradásának törvénye szerint U\_i \= K\_f, így 9\.81 \\, \\text\{J\} \= \\frac\{1\}\{2\} \(1 \\, \\text\{kg\}\) v\_f^2.

Ebből a sebesség v\_f \= \\sqrt\{\\frac\{2 \\times 9\.81 \\, \\text\{J\}\}\{1 \\, \\text\{kg\}\}\} \\approx 4\.43 \\, \\text\{m/s\}.

A Teljesítmény Fogalma: A Munkavégzés Sebessége

A teljesítmény (P) azt adja meg, hogy milyen gyorsan végeznek munkát, vagy milyen gyorsan alakul át az energia. Matematikailag a teljesítmény a végzett munka és az eltelt idő hányadosa:

P \= \\frac\{W\}\{t\}

A teljesítményt az energia idő szerinti deriváltjaként is definiálhatjuk:

P \= \\frac\{dE\}\{dt\}

A teljesítmény mértékegysége a Watt (W), amely megegyezik az 1 Joule per másodperccel (1 J/s).

Teljesítmény Állandó Erő Esetén

Ha egy állandó \\mathbf\{F\} erő egy testet \\mathbf\{v\} sebességgel mozgat, akkor a teljesítmény:

P \= \\mathbf\{F\} \\cdot \\mathbf\{v\} \= \|\\mathbf\{F\}\| \|\\mathbf\{v\}\| \\cos \\phi

ahol \\phi az erő és a sebesség közötti szög.

Feladat 5: Teljesítmény Számítása

Egy daru egy 500 kg tömegű terhet 10 méter magasra emel fel 20 másodperc alatt állandó sebességgel. Mekkora a daru által kifejtett átlagos teljesítmény?

Megoldás:

A daru által végzett munka a gravitáció ellenében: W \= mgh \= \(500 \\, \\text\{kg\}\) \(9\.81 \\, \\text\{m/s\}^2\) \(10 \\, \\text\{m\}\) \= 49050 \\, \\text\{J\}.

Az átlagos teljesítmény: P \= \\frac\{W\}\{t\} \= \\frac\{49050 \\, \\text\{J\}\}\{20 \\, \\text\{s\}\} \= 2452\.5 \\, \\text\{W\}.

A Hatásfok: A Hasznos Munkavégzés Mértéke

A valóságban az energiaátalakítások sosem tökéletesek; mindig van valamennyi energiaveszteség, leggyakrabban hő formájában. A hatásfok (\\eta) azt adja meg, hogy egy rendszer a befektetett energiának vagy munkának mekkora hányadát képes hasznos munkává vagy energiává alakítani:

\\eta \= \\frac\{W\_\{hasznos\}\}\{W\_\{befektetett\}\} \= \\frac\{E\_\{hasznos\}\}\{E\_\{befektetett\}\}

A hatásfok mindig 0 és 1 (vagy 0% és 100%) közötti érték.

Példa a Hatásfokra

Egy elektromos motor 1000 J elektromos energiát vesz fel, és ennek hatására 800 J mechanikai munkát végez. A motor hatásfoka \\eta \= \\frac\{800 \\, \\text\{J\}\}\{1000 \\, \\text\{J\}\} \= 0\.8, vagyis 80%.

Feladat 6: Hatásfok Számítása

Egy benzinmotor 50000 J kémiai energiát alakít át, miközben 12500 J mechanikai munkát végez. Mekkora a motor hatásfoka?

Megoldás:

A motor hatásfoka: \\eta \= \\frac\{12500 \\, \\text\{J\}\}\{50000 \\, \\text\{J\}\} \= 0\.25, vagyis 25%.

További Összetett Feladatok a Munka, Energia és Teljesítmény Témakörében

Összetett Feladat 1: Lejtőn Csúszó Test

Egy 5 kg tömegű test egy 30

Helyzeti Energia Szamitasa

A Helyzeti Energia Számítása: Részletes Útmutató

Ebben az átfogó útmutatóban részletesen feltárjuk a helyzeti energia fogalmát, a számításának módjait, a különböző típusait és azok gyakorlati alkalmazásait. Célunk, hogy egy olyan mélyreható ismeretanyagot nyújtsunk, amely mindenki számára érthetővé teszi a potenciális energia világát, legyen szó diákokról, tanárokról vagy a fizika iránt érdeklődő laikusokról.

Mi a Helyzeti Energia (Potenciális Energia)?

A helyzeti energia, más néven potenciális energia, egy olyan energiaforma, amely egy objektum helyzetéből vagy konfigurációjából adódik egy erőmezőn belül. Ez azt jelenti, hogy az objektum képes munkát végezni a helyzetének vagy konfigurációjának megváltozásával. A potenciális energia nem önmagában létezik, hanem mindig egy erőmezőhöz kapcsolódik, mint például a gravitációs mező, az elektromos mező vagy a rugalmas erő tere.

A Gravitációs Potenciális Energia

A leggyakrabban emlegetett formája a helyzeti energiának a gravitációs potenciális energia. Ez az energia egy objektum tömegéből és a gravitációs mezőben elfoglalt magasságából származik. Minél magasabban van egy objektum a referencia szinthez képest (általában a Föld felszíne), annál nagyobb a gravitációs potenciális energiája. Amikor ez az objektum leesik, a potenciális energia mozgási energiává alakul át.

A Gravitációs Potenciális Energia Képlete

A gravitációs potenciális energia (E\_p) számításának képlete a következő:

\\mathbf\{E\_p \= m \\cdot g \\cdot h\}

ahol:

• \\mathbf\{m\} az objektum tömege (kilogrammban, kg)
• \\mathbf\{g\} a gravitációs gyorsulás a Föld felszínén (körülbelül 9\.81 \\, m/s^2)
• \\mathbf\{h\} az objektum magassága a referencia szinthez képest (méterben, m)

Példa a Gravitációs Potenciális Energia Számítására

Képzeljünk el egy 2 \\, kg tömegű könyvet, amely egy 1\.5 \\, m magas polcon van. A könyv gravitációs potenciális energiája a Föld felszínéhez képest:

\\mathbf\{E\_p \= 2 \\, kg \\cdot 9\.81 \\, m/s^2 \\cdot 1\.5 \\, m \= 29\.43 \\, J\}

Tehát a könyv 29\.43 \\, Joule gravitációs potenciális energiával rendelkezik.

A Referencia Szint Fontossága

Fontos megjegyezni, hogy a gravitációs potenciális energia relatív fogalom, mivel függ a választott referencia szinttől. Általában a Föld felszínét tekintjük referencia szintnek, ahol a magasság h\=0, és így a potenciális energia is nulla. Azonban bizonyos problémák esetén más referencia szintek is praktikusak lehetnek.

A Rugalmas Potenciális Energia

Egy másik fontos típusa a helyzeti energiának a rugalmas potenciális energia. Ez az energia akkor tárolódik egy rugalmas testben (például egy rugóban), amikor azt megnyújtják vagy összenyomják az eredeti egyensúlyi helyzetéhez képest. A rugalmas erő, amely visszaállítja a rugót az egyensúlyi helyzetébe, végzi a munkát.

A Rugalmas Potenciális Energia Képlete

A rugalmas potenciális energia (E\_\{pr\}) számításának képlete a következő:

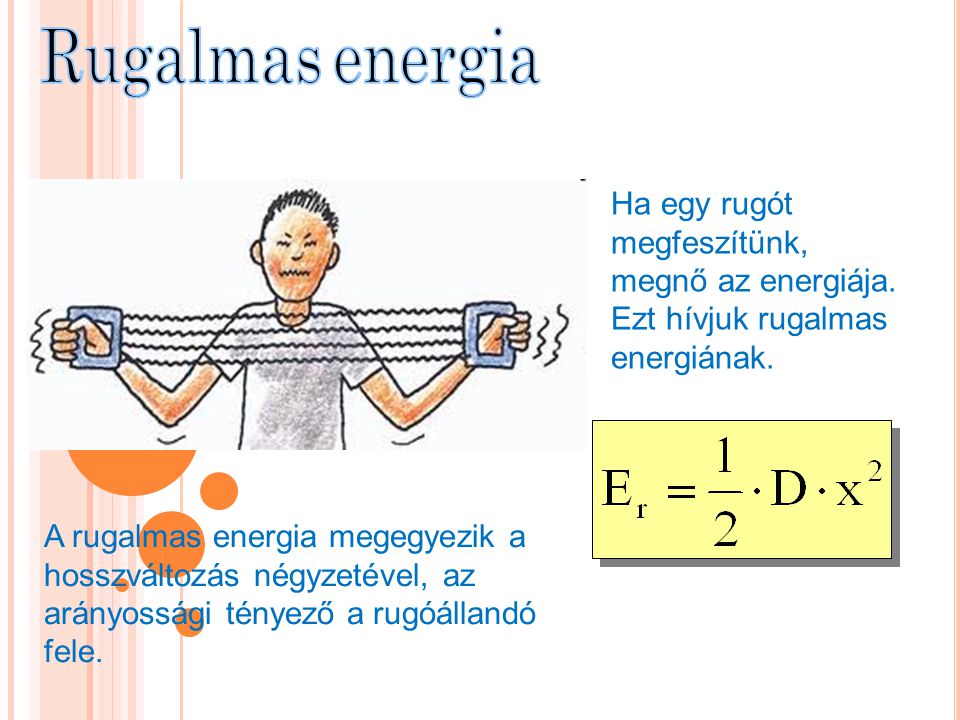
\\mathbf\{E\_\{pr\} \= \\frac\{1\}\{2\} \\cdot k \\cdot x^2\}

ahol:

• \\mathbf\{k\} a rugó rugóállandója (Newton/méterben, N/m), amely a rugó merevségét jellemzi.
• \\mathbf\{x\} a rugó megnyúlása vagy összenyomódása az egyensúlyi helyzetéhez képest (méterben, m).

Példa a Rugalmas Potenciális Energia Számítására

Tekintsünk egy rugót, amelynek rugóállandója 100 \\, N/m. Ha ezt a rugót 0\.1 \\, m-rel megnyújtjuk, a benne tárolt rugalmas potenciális energia:

\\mathbf\{E\_\{pr\} \= \\frac\{1\}\{2\} \\cdot 100 \\, N/m \\cdot \(0\.1 \\, m\)^2 \= 0\.5 \\, J\}

Tehát a megnyújtott rugó 0\.5 \\, Joule rugalmas potenciális energiával rendelkezik.

Egyéb Potenciális Energia Típusok

A gravitációs és a rugalmas potenciális energia mellett léteznek más formái is a helyzeti energiának:

• Elektromos potenciális energia: Két elektromos töltés közötti kölcsönhatásból származik.
• Mágneses potenciális energia: Mágneses mezőben lévő mágneses dipólus energiája.
• Kémiai potenciális energia: Az atomok és molekulák közötti kémiai kötésekben tárolt energia.
• Nukleáris potenciális energia: Az atommagban lévő nukleonok közötti kölcsönhatásból származó energia.

Bár ezek nem közvetlenül a “helyzetből” adódnak a szó szoros értelmében, mégis potenciális energiának nevezzük őket, mert egy adott konfigurációban tárolódnak, és felszabadulhatnak, munkát végezve.

A Helyzeti Energia Számításának Általános Elvei

Általánosságban elmondható, hogy a potenciális energia számítása egy adott erőmezőben a következőképpen történik:

1. Meg kell határozni az erőmezőt (pl. gravitációs, rugalmas).
2. Ki kell választani egy referencia pontot vagy konfigurációt, ahol a potenciális energia nulla.
3. A potenciális energia a munkával egyenlő, amelyet az erőmező végez ahhoz, hogy az objektumot a referencia pontból az aktuális helyzetébe vagy konfigurációjába vigye (vagy fordítva, az aktuális helyzetből a referencia pontba).

A Munkavégzés és a Potenciális Energia Kapcsolata

A potenciális energia szorosan kapcsolódik a munkavégzés fogalmához. Ha egy konzervatív erő (mint a gravitációs erő vagy a rugalmas erő) munkát végez egy objektumon, akkor a rendszer potenciális energiája megváltozik. A munkavégzés nagysága egyenlő a potenciális energia változásának negatívjával:

\\mathbf\{W \= \-\\Delta E\_p\}

Ez azt jelenti, hogy ha az erő munkát végez az objektumon (pl. egy leeső tárgy esetén a gravitáció), akkor a potenciális energia csökken. Ha pedig külső erő munkát végez az objektumon a konzervatív erő ellenében (pl. egy tárgy felemelése), akkor a potenciális energia nő.

A Helyzeti Energia Gyakorlati Alkalmazásai

A helyzeti energia fogalma és számítása számos területen kulcsfontosságú:

Energiatermelés

A vízerőművek a gravitációs potenciális energiát használják fel elektromos áram előállítására. A magasabban elhelyezkedő víztározókban tárolt víz potenciális energiával rendelkezik, amely mozgási energiává alakul át, amikor a vizet leengedik a turbinákon keresztül, megforgatva azokat és generátorokat hajtva.

Mechanikai Rendszerek

A rugók széles körben alkalmazásra kerülnek mechanikai rendszerekben, például felfüggesztésekben, órákban és különféle eszközökben. A bennük tárolt rugalmas potenciális energia lehetővé teszi a mozgást és az erő kifejtését.

Sport és Szórakozás

A hullámvasutak működése nagymértékben a gravitációs potenciális energián alapul. A kocsikat egy magas pontra húzzák fel, ahol nagy a potenciális energiájuk, majd ez az energia mozgási energiává alakul át a lejtőkön lefelé haladva.

Tárolt Energia

A akkumulátorokban és más energiatároló eszközökben kémiai potenciális energia tárolódik, amely elektromos energiává alakítható át szükség esetén.

Összefoglalás

A helyzeti energia vagy potenciális energia egy alapvető fogalom a fizikában, amely egy objektum helyzetéből vagy konfigurációjából adódik egy erőmezőn belül. Két fő típusát vizsgáltuk részletesen: a gravitációs potenciális energiát (E\_p \= m \\cdot g \\cdot h) és a rugalmas potenciális energiát (E\_\{pr\} \= \\frac\{1\}\{2\} \\cdot k \\cdot x^2). Megbeszéltük a számításuk módjait, a referencia szint fontosságát és a gyakorlati alkalmazásaikat az energiatermeléstől a mechanikai rendszereken át a sportig.

Reméljük, hogy ez a részletes útmutató segített megérteni a helyzeti energia lényegét és számításának módjait. Ha további kérdései vannak, ne habozzon feltenni!

A Gravitációs Potenciális Energia Mélyebben

A gravitációs potenciális energia nem csupán egy egyszerű képletet takar. Valójában a gravitációs mezőben végzett munka eredménye, amikor egy tömeget egy adott pontból egy másik pontba mozgatunk. A gravitációs erő egy konzervatív erő, ami azt jelenti, hogy a munkavégzése nem függ az úttól, csupán a kezdő- és végpont helyzetétől.

A Gravitációs Erő és a Munkavégzés

A Föld felszínén egy m tömegű objektumra ható gravitációs erő lefelé irányul, és nagysága F\_g \= m \\cdot g. Ha ezt az objektumot függőlegesen felfelé mozgatjuk egy h magasságra, akkor a külső erőnek (amely legyőzi a gravitációt) W \= F \\cdot d \= \(m \\cdot g\) \\cdot h munkát kell végeznie. Ez a bevitt munka tárolódik az objektumban gravitációs potenciális energiaként.

A Potenciális Energia Függése a Magasságtól

Ahogy a képlet is mutatja (E\_p \= m \\cdot g \\cdot h), a gravitációs potenciális energia egyenesen arányos az objektum tömegével és a referencia szint feletti magasságával. Egy kétszer akkora tömegű objektum azonos magasságban kétszer akkora potenciális energiával rendelkezik. Hasonlóképpen, egy objektum kétszer akkora magasságban kétszer akkora potenciális energiával rendelkezik (ugyanazon tömeg mellett).

Általános Gravitációs Potenciális Energia

A Föld felszínétől távolabb, vagy két tetszőleges tömeg közötti gravitációs potenciális energia leírásához az általános gravitációs törvényt kell használnunk. Két m\_1 és m\_2 tömeg közötti gravitációs potenciális energia, amelyek r távolságra vannak egymástól:

\\mathbf\{U \= \-G \\frac\{m\_1 m\_2\}\{r\}\}

ahol G az univerzális gravitációs állandó (6\.674 \\times 10^\{\-11\} \\, N \\cdot m^2/kg^2). Ebben az esetben a referencia pont a végtelen távolság (r \\rightarrow \\infty), ahol a potenciális energia nulla.

A Föld felszínénél alkalmazott E\_p \= m \\cdot g \\cdot h képlet valójában ennek az általánosabb képletnek egy közelítése, amikor a magasság h sokkal kisebb, mint a Föld sugara.

A Rugalmas Potenciális Energia Részletesebben

A rugalmas potenciális energia a rugalmas erő munkájának eredménye. A Hooke-törvény szerint egy ideális rugó által kifejtett erő (F\_r) egyenesen arányos a rugó egyensúlyi helyzetétől való elmozdulásával (x):

\\mathbf\{F\_r \= \-k \\cdot x\}

A negatív előjel azt jelzi, hogy a rugóerő mindig az elmozdulással ellentétes irányú, azaz visszaállító erő.

A Munkavégzés a Rugó Megnyújtásakor vagy Összenyomásakor

Ahhoz, hogy egy rugót megnyújtsunk vagy összenyomjunk egy x távolsággal, külső erőre van szükség, amely legyőzi a rugóerőt. Az ehhez szükséges munka a rugalmas potenciális energiában tárolódik. A munkát az erő integráljával számíthatjuk ki az elmozdulás mentén:

\\mathbf\{W \= \\int\_\{0\}^\{x\} F\_\{ext\} \\, dx \= \\int\_\{0\}^\{x\} kx \\, dx \= \\frac\{1\}\{2\} k x^2\}

Mivel a munkavégzés egyenlő a potenciális energia megváltozásával (a referencia pont a x\=0 egyensúlyi helyzet), kapjuk a rugalmas potenciális energia képletét: E\_\{pr\} \= \\frac\{1\}\{2\} k x^2.

A Rugóállandó Jelentősége

A rugóállandó (k) a rugó merevségének mértéke. Egy nagy k értékű rugó merevebb, nagyobb erőre van szükség az azonos mértékű megnyújtásához vagy öss

Helyzeti Energia Kiszamitasa

A Helyzeti Energia Kiszámítása: A Potenciális Energia Részletes Megközelítése

A helyzeti energia, más néven potenciális energia, a fizikában egy test vagy rendszer energiájának azon összetevője, amely a test vagy a rendszer helyzetéből vagy konfigurációjából adódik. Ez az energia tárolt formában van jelen, és képes munkát végezni, ha a rendszer megváltoztatja a helyzetét vagy konfigurációját. A helyzeti energia kulcsfontosságú fogalom a mechanikában, az elektromágnességben és más fizikai területeken is. Ebben a részletes útmutatóban mélyrehatóan megvizsgáljuk a helyzeti energia fogalmát, a különböző típusait, a kiszámításának módjait, valamint a gyakorlati alkalmazásait.

A Helyzeti Energia Alapjai

Ahhoz, hogy megértsük a helyzeti energia kiszámítását, először tisztáznunk kell magát a fogalmat. A potenciális energia egy olyan energiaforma, amely egy objektum vagy rendszer relatív helyzetéből, elrendezéséből vagy állapotából származik. Nem mozgással, hanem a potenciállal van összefüggésben, hogy mozgást hozzon létre. Gondoljunk egy magasban tartott kőre: amíg tartjuk, nem mozog, de rendelkezik potenciális energiával, amely felszabadul, ha elengedjük, és a gravitáció hatására leesik.

A Potenciális Energia Különböző Típusai

A potenciális energiának többféle formája létezik, amelyek különböző kölcsönhatásokhoz kapcsolódnak. A leggyakrabban előforduló típusok a következők:

Gravitációs Potenciális Energia

A gravitációs potenciális energia egy objektum tömegéből és a gravitációs mezőben elfoglalt helyzetéből adódik. Minél magasabban van egy objektum a Föld felszínéhez képest (vagy egy másik gravitációs testhez képest), annál nagyobb a gravitációs potenciális energiája. A gravitációs potenciális energia kiszámításának képlete a következő:

\\Large E\_p \= mgh

ahol:

• \(E_p\) a gravitációs potenciális energia (joule-ban mérve)
• \(m\) az objektum tömege (kilogrammban mérve)
• \(g\) a gravitációs gyorsulás (a Földön körülbelül \(9.81 \, m/s^2\))
• \(h\) az objektum magassága egy referencia szinthez képest (méterben mérve)

A referencia szint megválasztása önkényes, de a számítások szempontjából konzisztensnek kell lennie. Gyakran a Föld felszínét választják referencia szintnek, ahol a magasság \(h=0\), és így a potenciális energia is nulla.

Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmasan deformálható objektumban (például egy rugóban vagy egy gumiszalagban) tárolt energia, amelyet az objektum alakjának megváltoztatása okoz. Ha egy rugót megnyújtunk vagy összenyomunk, munkát végzünk rajta, és ez a munka rugalmas potenciális energiaként tárolódik. A rugalmas potenciális energia kiszámításának képlete a Hooke-törvényen alapul:

\\Large E\_p \= \\frac\{1\}\{2\}kx^2

ahol:

• \(E_p\) a rugalmas potenciális energia (joule-ban mérve)
• \(k\) a rugóállandó (newton per méterben mérve), amely a rugó merevségét jellemzi

• \(x\) a rugó egyensúlyi helyzetétől való elmozdulás (méterben mérve)

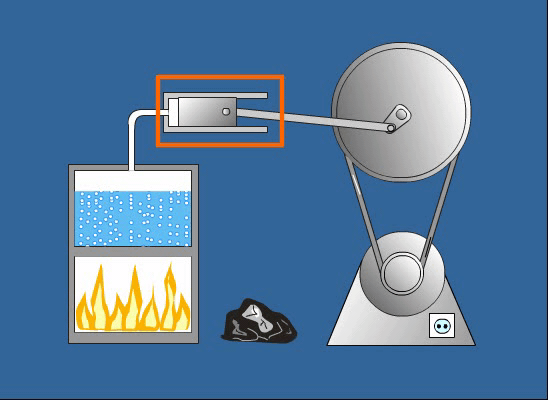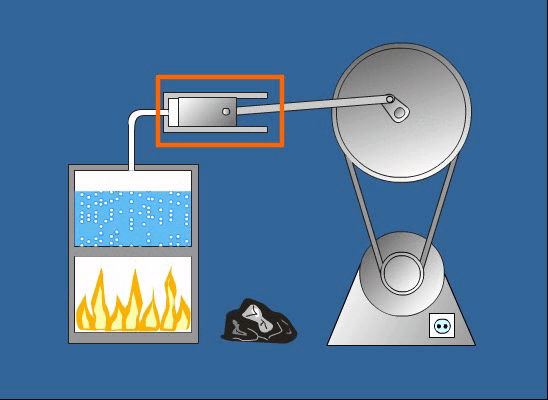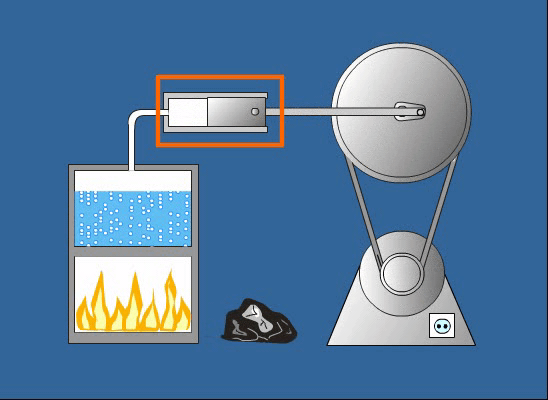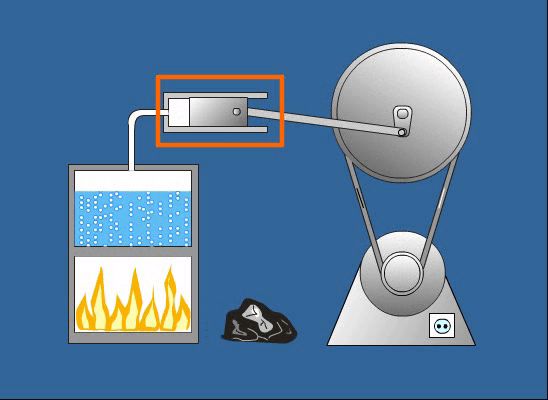
Minél nagyobb a rugóállandó vagy az elmozdulás, annál nagyobb a tárolt rugalmas potenciális energia.

Elektromos Potenciális Energia

Az elektromos potenciális energia elektromos töltések rendszerében tárolt energia, amely a töltések egymáshoz viszonyított helyzetéből adódik. Két azonos előjelű töltés közelebb hozása növeli az elektromos potenciális energiát, mivel munkát kell végeznünk a taszítóerő ellenében. Két ellentétes előjelű töltés közelebb hozása csökkenti az elektromos potenciális energiát, mivel a vonzóerő munkát végez.

Két ponttöltés \(q_1\) és \(q_2\) elektromos potenciális energiája \(r\) távolságban a következőképpen számítható:

\\Large E\_p \= k\_e \\frac\{q\_1 q\_2\}\{r\}

ahol \(k_e\) a Coulomb-állandó (\(8.9875 \times 10^9 \, N \cdot m^2/C^2\)).

Mágneses Potenciális Energia

A mágneses potenciális energia mágneses mezőben elhelyezkedő mágneses dipólus energiája. Például egy iránytű tűjének mágneses potenciális energiája függ a Föld mágneses mezőjéhez viszonyított orientációjától. A mágneses potenciális energia bonyolultabb képletekkel írható le, amelyek figyelembe veszik a mágneses momentumot és a mágneses mező erősségét.

Kémiai Potenciális Energia

A kémiai potenciális energia az atomok és molekulák közötti kémiai kötésekben tárolt energia. Ez az energia szabadul fel kémiai reakciók során, például égéskor vagy emésztéskor. Bár nem közvetlenül a helyzettel kapcsolatos a makroszkopikus értelemben, mégis potenciális energiának tekintjük, mivel a részecskék konfigurációjában rejlik.

Nukleáris Potenciális Energia

A nukleáris potenciális energia az atommagban lévő nukleonok (protonok és neutronok) közötti kölcsönhatásokból származik. Ez az energia szabadul fel nukleáris reakciók során, például a maghasadáskor vagy a magfúziókor. Hatalmas mennyiségű energia tárolható ebben a formában.

A Gravitációs Helyzeti Energia Részletes Kiszámítása

Mivel a “helyzeti energia kiszámítása” kifejezés a köznapi nyelvben leggyakrabban a gravitációs potenciális energiára utal, most ezt a típust fogjuk részletesebben megvizsgálni.

A Képlet Értelmezése

A gravitációs potenciális energia képlete, \(E_p = mgh\), egyszerű, de mély jelentéssel bír. A képlet azt mutatja, hogy a potenciális energia egyenesen arányos a test tömegével (\(m\)), a gravitációs gyorsulással (\(g\)), és a referencia szinthez viszonyított magasságával (\(h\)).

Tömeg (\(m\))

A tömeg az anyag mennyiségének mértéke egy objektumban. Minél nagyobb egy objektum tömege, annál nagyobb a gravitációs erő, amely hat rá, és annál nagyobb a potenciális energiája egy adott magasságban.

Gravitációs Gyorsulás (\(g\))

A gravitációs gyorsulás a gravitációs tér által egy objektumra kifejtett gyorsulás. A Föld felszínén ez az érték átlagosan \(9.81 \, m/s^2\). Más égitesteken (például a Holdon vagy a Marson) a gravitációs gyorsulás eltérő.

Magasság (\(h\))

A magasság az objektum vertikális távolsága egy kiválasztott referencia szinthez képest. A referencia szint lehet a Föld felszíne, egy épület alapja, vagy bármilyen más kényelmes pont. Fontos, hogy a számítás során következetesen ugyanazt a referencia szintet használjuk.

Példák a Gravitációs Potenciális Energia Kiszámítására

Nézzünk néhány példát a gravitációs potenciális energia kiszámítására, hogy jobban megértsük a képlet alkalmazását.

1. példa: Egy leeső alma

Egy \(0.2 \, kg\) tömegű alma egy \(3 \, m\) magas faágról esik le. Mennyi volt az alma gravitációs potenciális energiája, mielőtt leesett (a Föld felszínéhez képest)?

Adatok:

• Tömeg (\(m\)) = \(0.2 \, kg\)
• Magasság (\(h\)) = \(3 \, m\)
• Gravitációs gyorsulás (\(g\)) = \(9.81 \, m/s^2\)

A képletet alkalmazva:

\\Large E\_p \= mgh \= \(0\.2 \\, kg\) \\times \(9\.81 \\, m/s^2\) \\times \(3 \\, m\) \= 5\.886 \\, J

Tehát az alma gravitációs potenciális energiája a faágon \(5.886 \, joule\) volt.

2. példa: Egy hegy tetején lévő turista

Egy \(70 \, kg\) tömegű turista egy \(1500 \, m\) magas hegy tetején áll. Mennyi a turista gravitációs potenciális energiája a tengerszinthez képest?

Adatok:

• Tömeg (\(m\)) = \(70 \, kg\)
• Magasság (\(h\)) = \(1500 \, m\)
• Gravitációs gyorsulás (\(g\)) = \(9.81 \, m/s^2\)

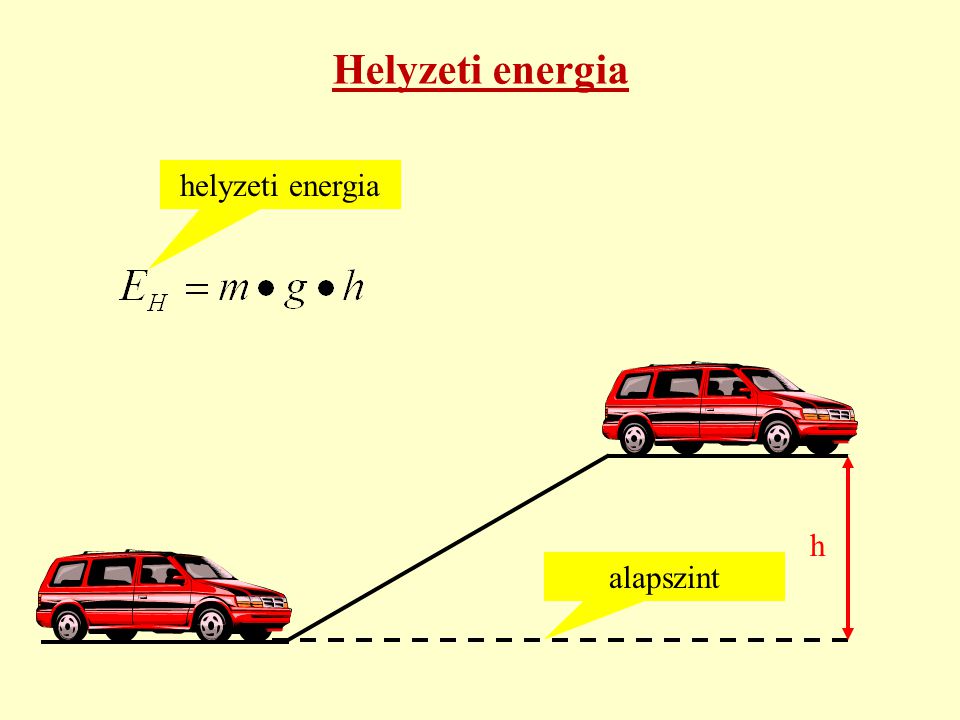
A képletet alkalmazva:

\\Large E\_p \= mgh \= \(70 \\, kg\) \\times \(9\.81 \\, m/s^2\) \\times \(1500 \\, m\) \= 1,030,050 \\, J \= 1030\.05 \\, kJ

A turista gravitációs potenciális energiája a tengerszinthez képest körülbelül \(1030.05 \, kilojoule\).

3. példa: Egy repülőgép

Egy \(50,000 \, kg\) tömegű repülőgép \(10,000 \, m\) magasan repül a tengerszint felett. Számítsuk ki a repülőgép gravitációs potenciális energiáját.

Adatok:

• Tömeg (\(m\)) = \(50,000 \, kg\)
• Magasság (\(h\)) = \(10,000 \, m\)
• Gravitációs gyorsulás (\(g\)) = \(9.81 \, m/s^2\)

A képletet alkalmazva:

\\Large E\_p \= mgh \= \(50,000 \\, kg\) \\times \(9\.81 \\, m/s^2\) \\times \(10,000 \\, m\) \= 4,905,000,000 \\, J \= 4\.905 \\, GJ

A repülőgép gravitációs potenciális energiája \(4.905 \, gigajoule\>.

A Referencia Szint Fontossága

Fontos megjegyezni, hogy a gravitációs potenciális energia értéke függ a választott referencia szinttől. Ha egy másik referencia szintet választunk, a magasság (\(h\)) értéke megváltozik, és így a potenciális energia értéke is. Azonban a potenciális energia különbsége két pont között független a referencia szint megválasztásától. Például, ha egy objektum \(h_1\) magasságból \(h_2\) magasságba esik, a potenciális energia változása \(mg(h_2 – h_1)\), ami nem függ attól, hogy a \(h=0\) szintet hol vettük fel.

A Rugalmas Helyzeti Energia Részletes Kiszámítása

Most nézzük meg a rugalmas potenciális energia kiszámítását részletesebben.

A Képlet Értelmezése

A rugalmas potenciális energia képlete, \(E_p = \frac{1}{2}kx^2\), azt mutatja, hogy a tárolt energia arányos a rugóállandóval (\(k\)) és az elmozdulás négyzetével (\(x^2\)).

Rugóállandó (\(k\))

A rugóállandó (\(k\)) a rugó merevségének mértéke. Nagyobb \(k\) érték merevebb rugót jelent, amelyhez nagyobb erő szükséges az azonos mértékű megnyújtáshoz vagy összenyomáshoz. A rugóállandót általában newton per méter (\(N/m\)) egységben mérik.

Elmozdulás (\(x\))

Az elmozdulás (\(x\)) a rugó egyensúlyi helyzetétől való távolságot jelenti. Ez lehet megnyúlás vagy összenyomás. A potenciális energia az elmozdulás négyzetével arányos, ami azt jelenti, hogy az elmozdulás kétszeresére növelése négyszeresére növeli a tárolt energiát.

Példák a Rugalmas Potenciális Energia Kiszámítására

Nézzünk néhány példát a rugalmas potenciális energia kiszámítására.

1. példa: Megnyújtott rugó

Egy rugó rugóállandója \(k = 100 \, N/m\). Mennyi a rugalmas potenciális energia, ha a rugót \(0.1 \, m\)-rel megnyújtjuk?

Adatok:

• Rugóállandó (\(k\)) = \(100 \, N/m\)
• Elmozdulás (\(x\)) = \(0.1 \, m\)

A képletet alkalmazva:

\\Large E\_p \= \\frac\{1\}\{2\}kx^2 \= \\frac\{1\}\{2\} \\times \(100 \\, N/m\) \\times \(0\.1 \\, m\)^2 \= \\frac\{1\}\{2\} \\times 100 \\times 0\.01 \\, J \= 0\.5 \\, J

A rugalmas potenciális energia \(0.5 \, joule

Helyzeti Energia Fogalma

A Helyzeti Energia Fogalma: Mélyreható Értelmezés és Alkalmazások

Mi a Helyzeti Energia? A Potenciális Energia Alapjai

A helyzeti energia, más néven potenciális energia, egy olyan tárolt energiaforma, amely egy objektum helyzetéből, konfigurációjából vagy állapotából ered. Ez az energia akkor képes munkát végezni, amikor az objektum felszabadul, és helyzete vagy konfigurációja megváltozik. A helyzeti energia nem önmagában létezik, hanem mindig egy erőtérrel (például gravitációs, elektromos vagy rugalmas) kölcsönhatásban lévő objektumhoz kapcsolódik. Amikor egy objektum egy ilyen erőtérben mozog, a mező munkát végezhet rajta, megváltoztatva a helyzeti energiáját, vagy az objektum végezhet munkát a mező ellen, szintén megváltoztatva a helyzeti energiáját.

A potenciális energia fogalma kulcsfontosságú a fizika számos területén, a klasszikus mechanikától az elektromágnességen át a modern fizikáig. Segítségével leírhatjuk a rendszerek stabilitását, az energiaátalakulásokat és a mozgás törvényeit. A mindennapi életben is gyakran találkozunk a helyzeti energiával, például amikor egy hegy tetején álló kőnek potenciális energiája van a gravitációs mezőben, vagy amikor egy megfeszített rugóban rugalmas helyzeti energia tárolódik.

A Gravitációs Helyzeti Energia: Magyarázat és Képlet

A gravitációs helyzeti energia egy objektum tömegéből és a gravitációs mezőben elfoglalt helyzetéből származó potenciális energia. A Föld felszínének közelében a gravitációs mező közelítőleg homogénnek tekinthető, és a gravitációs helyzeti energia a következő képlettel számítható ki:

\\displaystyle E\_p \= mgh

ahol:

• \\displaystyle E\_p a gravitációs helyzeti energia (joule-ban mérve, J)
• \\displaystyle m az objektum tömege (kilogrammban mérve, kg)
• \\displaystyle g a gravitációs gyorsulás (a Földön körülbelül \\displaystyle 9\.81 \\, m/s^2)
• \\displaystyle h az objektum magassága egy referencia-szinthez képest (méterben mérve, m)

Fontos megjegyezni, hogy a referencia-szint megválasztása önkényes, de a helyzeti energia *változása* független ettől a választástól. Például, ha egy objektumot egy bizonyos magasságról leejtünk, a gravitációs helyzeti energiájának csökkenése mindig ugyanakkora lesz, függetlenül attól, hogy a referencia-szintet a földfelszínen vagy egy annál alacsonyabb ponton vesszük fel.

Példák a Gravitációs Helyzeti Energiára

• Egy polcon álló könyvnek gravitációs helyzeti energiája van a földhöz képest. Minél magasabban van a polc, annál nagyobb ez az energia. Amikor a könyv leesik, ez a helyzeti energia mozgási energiává alakul.
• Egy víztározóban felgyülemlett víznek jelentős gravitációs helyzeti energiája van a völgyben lévő turbinákhoz képest. Amikor a vizet leengedik, ez az energia a turbinákat meghajtva elektromos energiává alakul.
• Egy hegycsúcson lévő síelőnek nagy a gravitációs helyzeti energiája a völgy aljához képest. Leereszkedés közben ez az energia részben mozgási energiává, részben pedig hővé alakul a súrlódás miatt.

A Rugalmas Helyzeti Energia: A Megfeszített Rugók Energiája

A rugalmas helyzeti energia egy rugalmasan deformált objektumban (például egy megfeszített vagy összenyomott rugóban) tárolt potenciális energia. Ez az energia akkor keletkezik, amikor egy külső erő munkát végez a rugón, megváltoztatva annak alakját. A rugalmas helyzeti energia a rugó eredeti alakjába való visszatérésre való törekvéséből származik.

Egy ideális rugó által tárolt rugalmas helyzeti energia a Hooke-törvény alapján számítható ki:

\\displaystyle E\_p \= \\frac\{1\}\{2\}kx^2

ahol:

• \\displaystyle E\_p a rugalmas helyzeti energia (joule-ban, J)
• \\displaystyle k a rugóállandó (newton per méterben mérve, N/m), amely a rugó merevségét jellemzi
• \\displaystyle x a rugó egyensúlyi helyzetétől való elmozdulás (méterben, m)

A képletből látható, hogy a rugalmas helyzeti energia arányos az elmozdulás négyzetével. Ez azt jelenti, hogy a rugó megnyújtásának vagy összenyomásának kétszerese négyszeresére növeli a tárolt energiát.

Példák a Rugalmas Helyzeti Energiára

• Egy megfeszített íjban rugalmas helyzeti energia tárolódik. Amikor az íjhúr elengedik, ez az energia a nyílnak mozgási energiává alakul.
• Egy összenyomott rugóban, például egy autó felfüggesztésében, rugalmas helyzeti energia van. Amikor a rugó kinyílik, ez az energia hatással van az autó mozgására.
• Egy gumiszalag megnyújtásakor rugalmas helyzeti energiát tárolunk benne. Amikor elengedjük, ez az energia más objektumok (például egy papírgolyó) mozgatására használható fel.

Az Elektromos Helyzeti Energia: Töltött Részecskék Kölcsönhatása

Az elektromos helyzeti energia két vagy több elektromosan töltött részecske relatív helyzetéből származó potenciális energia. Ez az energia az elektromos mező által a töltött részecskékre kifejtett erővel kapcsolatos. Két ponttöltés közötti elektromos helyzeti energia a Coulomb-törvényből vezethető le:

\\displaystyle U \= k \\frac\{q\_1 q\_2\}\{r\}

ahol:

• \\displaystyle U az elektromos helyzeti energia (joule-ban, J)
• \\displaystyle k a Coulomb-állandó (\\displaystyle \\approx 8\.9875 \\times 10^9 \\, N \\cdot m^2/C^2)
• \\displaystyle q\_1 és \\displaystyle q\_2 a két ponttöltés nagysága (coulomb-ban, C)
• \\displaystyle r a két töltés közötti távolság (méterben, m)

Az elektromos helyzeti energia pozitív, ha a két töltés azonos előjelű (mindkettő pozitív vagy mindkettő negatív), és negatív, ha ellentétes előjelűek. A nulla helyzeti energia konvenciója általában az, hogy a töltések végtelen távolságban vannak egymástól.

Példák az Elektromos Helyzeti Energiára

• Egy atommag és egy elektron közötti elektromos helyzeti energia felelős az atom stabilitásáért. Az elektron alacsonyabb potenciális energiájú pályákra törekszik.
• Két azonos előjelű töltés közeledése növeli az elektromos helyzeti energiát, mivel munkát kell végezni az elektromos taszítóerő ellen.
• Két ellentétes előjelű töltés közeledése csökkenti az elektromos helyzeti energiát, mivel az elektromos vonzóerő munkát végez a töltéseken.

A Kémiai Helyzeti Energia: Az Atomok Kötéseiben Tárolt Energia

A kémiai helyzeti energia az atomok és molekulák kötéseiben tárolt potenciális energia. Ez az energia az elektronok és az atommagok közötti elektromágneses kölcsönhatásokból származik. Kémiai reakciók során ezek a kötések felbomolhatnak és újak jöhetnek létre, ami energia felszabadulásával vagy elnyelésével járhat.

A kémiai helyzeti energia nem olyan egyszerűen számítható ki, mint a gravitációs vagy a rugalmas helyzeti energia, mivel az atomok és molekulák komplex elektronstruktúrájától függ. Azonban a kémiai reakciók során felszabaduló vagy elnyelt hőmennyiség (entalpiaváltozás) közvetlenül kapcsolódik a kémiai kötésekben bekövetkező energiaváltozásokhoz.

Példák a Kémiai Helyzeti Energiára

• A fa vagy a fosszilis tüzelőanyagok kémiai helyzeti energiát tartalmaznak. Égés során ez az energia hővé és fényé alakul.
• Az élelmiszerekben tárolt kémiai energia a szervezetünk számára biztosítja a működéshez szükséges energiát. A metabolizmus során a komplex molekulák lebomlanak, és energia szabadul fel.
• Az akkumulátorokban tárolt kémiai energia elektromos energiává alakítható kémiai reakciók révén.

A Magasságtól Függő Helyzeti Energia Részletesebben

A magasságtól függő helyzeti energia, ahogy korábban említettük, a gravitációs helyzeti energia speciális esete a Föld felszínének közelében. A \\displaystyle E\_p \= mgh képlet jól közelíti ezt az energiát, feltéve, hogy a magasságváltozás nem túl nagy, és a gravitációs gyorsulás (\\displaystyle g) konstansnak tekinthető.

Ha azonban nagy magasságváltozásokról van szó, vagy ha távolabb kerülünk a Földtől, a gravitációs erő már nem tekinthető konstansnak, és a helyzeti energia képlete is megváltozik. Általánosabban, a két tömeg közötti gravitációs potenciális energia a következőképpen írható le:

\\displaystyle U \= \-G \\frac\{m\_1 m\_2\}\{r\}

ahol:

• \\displaystyle U a gravitációs potenciális energia
• \\displaystyle G a gravitációs állandó (\\displaystyle \\approx 6\.674 \\times 10^\{\-11\} \\, N \\cdot m^2/kg^2)
• \\displaystyle m\_1 és \\displaystyle m\_2 a két tömeg
• \\displaystyle r a két tömeg középpontja közötti távolság

Ebben az esetben a nulla potenciális energia konvenciója az, hogy a két tömeg végtelen távolságban van egymástól. A negatív előjel azt jelzi, hogy a gravitációs erő vonzó, és munkát kell végezni a tömegek szétválasztásához.

Alkalmazások a Csillagászatban

A gravitációs helyzeti energia kulcsszerepet játszik a csillagászatban. Például:

• A bolygók Nap körüli mozgását a Nap gravitációs helyzeti energiája és a bolygók mozgási energiája határozza meg.
• A csillagok kialakulása során a gázfelhők gravitációs összehúzódása helyzeti energia felszabadulásával jár, ami a csillag felmelegedéséhez vezet.
• A fekete lyukak rendkívül erős gravitációs terében a helyzeti energia fogalma relativisztikus korrekciókat igényel.

A Rugóállandó és a Rugalmas Helyzeti Energia Kapcsolata Mélyebben

A rugóállandó (\\displaystyle k) egy mérőszám, amely megmutatja, hogy egy rugó mennyire ellenáll a deformációnak. Nagyobb rugóállandó azt jelenti, hogy nagyobb erőre van szükség a rugó adott mértékű megnyújtásához vagy összenyomásához. A rugóállandó a rugó anyagától, méretétől és alakjától függ.

A rugalmas helyzeti energia (\\displaystyle E\_p \= \\frac\{1\}\{2\}kx^2) közvetlenül arányos a rugóállandóval. Ez azt jelenti, hogy egy merevebb rugó (nagyobb \\displaystyle k) ugyanakkora elmozdulás esetén több rugalmas helyzeti energiát tárol, mint egy lágyabb rugó (kisebb \\displaystyle k).

Energiatárolás Rugókkal

A rugók hatékonyan képesek energiát tárolni rugalmas helyzeti energia formájában. Ezt az elvet számos technológiai alkalmazásban kihasználják:

• A mechanikus órákban egy felhúzott rugó tárolja az energiát, amely a fogaskerekeken keresztül a mutatók mozgatására szolgál.
• A rugós mérlegek a rugó megnyúlásának mértékéből következtetnek a rájuk ható erőre (és így a mérendő tárgy tömegére).
• A járművek felfüggesztésében használt rugók elnyelik az útegyenetlenségekből származ

Mechanikai Energiafajtak

A Mechanikai Energia Fajtái: Átfogó Kézikönyv

A mechanikai energia a fizika egyik alapvető fogalma, amely egy test vagy rendszer mozgásával és helyzetével kapcsolatos energiát írja le. Ez az energiaforma kulcsfontosságú a makroszkopikus világ jelenségeinek megértéséhez, a mindennapi tapasztalatainktól kezdve a komplex mérnöki alkalmazásokig. Ebben a részletes útmutatóban feltárjuk a mechanikai energia különböző fajtáit, azok jellemzőit, megjelenési formáit és a velük kapcsolatos alapvető fizikai törvényeket.

A Mechanikai Energia Alapjai

A mechanikai energia fogalma szorosan kapcsolódik a munkavégzés képességéhez. Ha egy erő egy testet elmozdít, munkát végez rajta, és ez a munka megváltoztathatja a test mechanikai energiáját. A mechanikai energia két fő összetevőre bontható: a kinetikus energiára és a potenciális energiára. Ezek az energiafajták együttesen határozzák meg egy rendszer teljes mechanikai energiáját.

Kinetikus Energia: A Mozgás Energiája

A kinetikus energia egy test mozgásából származó energia. Minden olyan objektum, amely mozog, rendelkezik kinetikus energiával. Ennek az energiának a nagysága függ a test tömegétől és sebességétől. Minél nagyobb a test tömege vagy sebessége, annál nagyobb a kinetikus energiája. A kinetikus energia képlete a következő:

\\mathbf\{E\_k \= \\frac\{1\}\{2\}mv^2\}

ahol \(E_k\) a kinetikus energia, \(m\) a test tömege, és \(v\) a test sebessége.

Példák a Kinetikus Energiára

• Egy száguldó autó: Minél gyorsabban halad az autó, annál nagyobb a kinetikus energiája. Egy nehezebb autó azonos sebességnél szintén nagyobb kinetikus energiával rendelkezik.
• Egy repülő labda: A labda mozgása során kinetikus energiával rendelkezik. A dobás erőssége és a labda tömege befolyásolja ezt az energiát.
• Egy forgó kerék: A forgó kerék részei folyamatos mozgásban vannak, így a kerék rendelkezik kinetikus energiával.

A kinetikus energia nem csak a lineáris mozgáshoz kapcsolódik, hanem a forgó mozgáshoz is. A forgó testek forgási kinetikus energiával rendelkeznek, amely a test tehetetlenségi nyomatékától és szögsebességétől függ.

\\mathbf\{E\_\{rot\} \= \\frac\{1\}\{2\}I\\omega^2\}

ahol \(E_{rot}\) a forgási kinetikus energia, \(I\) a tehetetlenségi nyomaték, és \(\omega\) a szögsebesség.

Potenciális Energia: A Helyzetből Adódó Energia

A potenciális energia egy test helyzetéből vagy konfigurációjából származó tárolt energia. Ez az energia akkor szabadulhat fel, ha a test megváltoztatja a helyzetét vagy konfigurációját. A mechanikában két fő típusa van a potenciális energiának: a gravitációs potenciális energia és a rugalmas potenciális energia.

Gravitációs Potenciális Energia

A gravitációs potenciális energia egy testnek a gravitációs mezőben elfoglalt helyzetéből adódik. A Föld felszínén egy \(h\) magasságban lévő \(m\) tömegű test gravitációs potenciális energiája a következőképpen számítható ki:

\\mathbf\{E\_p \= mgh\}

ahol \(E_p\) a gravitációs potenciális energia, \(m\) a test tömege, \(g\) a gravitációs gyorsulás (a Földön körülbelül \(9.81 \, m/s^2\)), és \(h\) a test magassága egy referencia szinthez képest.

Példák a Gravitációs Potenciális Energiára

• Egy hegy tetején lévő kő: A kőnek magasságából adódóan gravitációs potenciális energiája van. Ha a kő leesik, ez az energia kinetikus energiává alakul át.
• Egy víztározóban lévő víz: A magasabban lévő víz gravitációs potenciális energiával rendelkezik, amelyet a vízerőművek elektromos áram előállítására használnak fel.
• Egy fán lévő alma: Az almának a földfelszínhez viszonyított magassága miatt gravitációs potenciális energiája van. Amikor leesik, ez az energia mozgási energiává alakul.

Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmasan deformálható test (például egy rugó vagy egy gumiszalag) megfeszítéséből vagy összenyomásából származik. A rugalmas erővel szemben végzett munka tárolódik ebben az energiaformában. Egy ideális rugó rugalmas potenciális energiája a következőképpen adható meg:

\\mathbf\{E\_\{elas\} \= \\frac\{1\}\{2\}kx^2\}

ahol \(E_{elas}\) a rugalmas potenciális energia, \(k\) a rugóállandó (amely a rugó merevségét jellemzi), és \(x\) a rugó egyensúlyi helyzetétől való elmozdulása.

Példák a Rugalmas Potenciális Energiára

• Egy megfeszített rugó: Amikor egy rugót megfeszítünk vagy összenyomunk, rugalmas potenciális energiát tárol. Ez az energia szabadul fel, amikor a rugó visszatér eredeti alakjába.
• Egy kilőtt nyíl: A megfeszített íj húrjában tárolt rugalmas potenciális energia alakul át a nyíl kinetikus energiájává.
• Egy trambulin: Amikor valaki ráugrik a trambulinra, a rugók megfeszülnek, rugalmas potenciális energiát tárolva, amely aztán visszalökő erőt fejt ki.

A Mechanikai Energia Megmaradása

Az egyik legfontosabb elv a fizikában az energia megmaradásának törvénye, amely kimondja, hogy egy zárt rendszer teljes energiája állandó marad, feltéve, hogy nincsenek nem-konzervatív erők (például súrlódás vagy légellenállás) munkája. A mechanikai energia esetében ez azt jelenti, hogy egy olyan rendszerben, ahol csak konzervatív erők hatnak, a kinetikus energia és a potenciális energia összege állandó marad:

\\mathbf\{E\_\{mech\} \= E\_k \+ E\_p \= állandó\}

Példák az Energia Megmaradására

• Egy ingamozgás: Amikor az inga a legmagasabb pontján van, a potenciális energiája maximális, a kinetikus energiája pedig nulla. Ahogy az inga lefelé mozog, a potenciális energia kinetikus energiává alakul át. A legalacsonyabb ponton a kinetikus energia maximális, a potenciális energia pedig minimális. Ideális esetben a teljes mechanikai energia (a kinetikus és a potenciális energia összege) állandó marad.

• Egy leeső tárgy: Amikor egy tárgyat elejtünk, a kezdeti magasságban gravitációs potenciális energiával rendelkezik. Ahogy esik, ez az energia fokozatosan kinetikus energiává alakul át. Közvetlenül a földbe csapódás előtt a kinetikus energia maximális, a potenciális energia pedig minimális (a referencia szinttől függően).

Nem-Konzervatív Erők és a Mechanikai Energia Disszipációja

A valóságban gyakran vannak jelen nem-konzervatív erők, mint például a súrlódás és a légellenállás. Ezek az erők munkát végeznek a rendszeren, és ez a munka nem tárolódik potenciális energiaként, hanem általában hővé alakul. Ebben az esetben a teljes mechanikai energia nem marad meg, hanem csökken. Ezt az energiacsökkenést disszipációnak nevezzük.

Példák a Mechanikai Energia Disszipációjára

• Egy csúszó tárgy: Amikor egy tárgy egy felületen csúszik, a súrlódási erő munkát végez, és a mechanikai energia egy része hővé alakul, felmelegítve a tárgyat és a felületet. Ennek eredményeként a tárgy mozgása lelassul és végül megáll.
• Egy fékező autó: Az autó fékezése során a kinetikus energia a fékekben súrlódási hővé alakul, ami lelassítja az autót.

A Mechanikai Energia Átalakulásai

A mechanikai energia különböző formái egymásba alakulhatnak. Láttuk már a potenciális energia kinetikus energiává való átalakulását egy leeső tárgy vagy egy inga esetében, és fordítva, a kinetikus energia potenciális energiává alakulását egy felfelé dobott labda esetében, amely eléri a legmagasabb pontját.

További Példák az Energia Átalakulásaira

• Egy vízerőmű: A víztározóban lévő víz gravitációs potenciális energiája a turbinákon átfolyva kinetikus energiává alakul, amely aztán elektromos generátort hajt meg.
• Egy autó motorja: A benzin kémiai energiája először hővé, majd a mozgó alkatrészek révén mechanikai energiává alakul.
• Egy szélmalom: A szél kinetikus energiája a lapátokat forgatva mechanikai energiává alakul, amelyet aztán különböző célokra lehet felhasználni.

A Mechanikai Energia Jelentősége és Alkalmazásai

A mechanikai energia megértése és hasznosítása alapvető fontosságú számos tudományterületen és technológiai alkalmazásban.

Mérnöki Alkalmazások

• Gépészet: A gépek tervezése és működtetése a mechanikai energia átalakításán és továbbításán alapul.
• Építőmérnökség: Az épületek és hidak stabilitásának és a terhelések elviselésének megértéséhez elengedhetetlen a mechanikai erők és energiák ismerete.

• Repüléstechnika: A repülőgépek mozgása és a felhajtóerő létrehozása a mechanikai elveken alapul.

Mindennapi Élet

• A közlekedési eszközök (autók, vonatok, kerékpárok) mechanikai energiát használnak a mozgáshoz.
• A háztartási gépek (mosógép, turmixgép) működéséhez mechanikai energiára van szükség.
• A sporteszközök (labdák, ütők) használata során a mechanikai energia átalakulásai figyelhetők meg.

Összefoglalás

A mechanikai energia a mozgással és a helyzettel kapcsolatos energia. Két fő fajtája van: a kinetikus energia (a mozgás energiája) és a potenciális energia (a helyzetből adódó tárolt energia, amely lehet gravitációs vagy rugalmas). Egy zárt rendszerben, ahol csak konzervatív erők hatnak, a mechanikai energia megmarad. A valóságban azonban nem-konzervatív erők is jelen lehetnek, amelyek a mechanikai energia disszipációjához vezetnek. A mechanikai energia megértése kulcsfontosságú a természeti jelenségek és a technológiai alkalmazások széles körének megértéséhez.

További Tudnivalók a Mechanikai Energiáról

A mechanikai energia fogalmának mélyebb megértéséhez érdemes megvizsgálni a munka-energia tételt is, amely összekapcsolja a munkát és az energiaváltozást. A tétel kimondja, hogy egy testre ható összes erő által végzett munka egyenlő a test kinetikus energiájának megváltozásával:

\\mathbf\{W\_\{net\} \= \\Delta E\_k \= E\_\{k,f\} \- E\_\{k,i\}\}

ahol \(W_{net}\) a nettó munka, \(\Delta E_k\) a kinetikus energia változása, \(E_{k,f}\) a végső kinetikus energia, és \(E_{k,i}\) a kezdeti kinetikus energia.

A Konzervatív Erők és a Potenciális Energia Kapcsolata

A potenciális energia fogalma szorosan kapcsolódik a konzervatív erőkkel. Egy erő akkor konzervatív, ha az általa végzett munka egy zárt úton nulla, vagy ha a két pont között végzett munka független az útvonaltól. A gravitációs erő és a rugalmas erő tipikus példái a konzervatív erőknek. A potenciális energia definíció szerint a konzervatív erő által végzett munka negatívja:

\\mathbf\{\\Delta U \= \-W\_c\}

ahol \(\Delta U\) a potenciális energia változása, és \(W_c\) a konzervatív erő által végzett munka.

A Mechanikai Energia Mérésének Egységei

A mechanikai energiát (mind a kinetikus, mind a potenciális formában) a Nemzetközi Mértékegységrendszerben (SI) joule-ban (J) mérik. Egy joule egyenlő egy newton méterrel (N·m), vagy alapegységekben \(kg \cdot m^2/s^2\).

Komplexebb Rendszerek Mechanikai Energiája

Több testből álló rendszerek esetében a teljes mechanikai energia az egyes testek kinetikus és potenciális energiáinak összege. Például egy bolygórendszerben a bolygók kinetikus energiájának és a bolygók közötti gravitációs potenciális energiának az összege adja a rendszer teljes mechanikai energiáját.

Molekuláris szintű Mechanikai Energia

Bár a mechanikai energia fogalmát leggyakrabban makroszkopikus objektum

Mechanikai Energia Megmaradas Torvenye

A Mechanikai Energia Megmaradásának Törvénye: A Fizika Egyik Alapköve

A mechanikai energia megmaradásának törvénye a fizika egyik legfontosabb és legszélesebb körben alkalmazható alapelve. Kimondja, hogy egy izolált rendszerben, ahol csak konzervatív erők (mint például a gravitációs erő vagy a rugalmas erő) hatnak, a mechanikai energia – vagyis a kinetikus energia és a potenciális energia összege – időben állandó marad. Ez azt jelenti, hogy az energia nem vész el, hanem csak átalakul egyik formájából a másikba. Ebben a részletes cikkben mélyrehatóan megvizsgáljuk ezt a fundamentális törvényt, feltárjuk a mögötte rejlő elveket, szemléletes példákon keresztül mutatjuk be alkalmazásait, és megvitatjuk a nem konzervatív erők hatását is.

A Mechanikai Energia Definíciója és Összetevői

A mechanikai energia egy rendszer azon képessége, hogy munkát végezzen a mozgása vagy a helyzete miatt. Két fő összetevője van: a kinetikus energia és a potenciális energia. Ahhoz, hogy teljes mértékben megértsük a mechanikai energia megmaradásának törvényét, elengedhetetlen, hogy tisztában legyünk ezen összetevők definíciójával és jelentésével.

A Kinetikus Energia: A Mozgás Energiája

A kinetikus energia egy test mozgásából származó energia. Minél nagyobb egy test tömege és minél gyorsabban mozog, annál nagyobb a kinetikus energiája. Matematikailag a kinetikus energia (E\_k) a következőképpen fejezhető ki:

\\mathbf\{E\_k \= \\frac\{1\}\{2\}mv^2\}

ahol \\mathbf\{m\} a test tömege, \\mathbf\{v\} pedig a sebessége. Ebből az egyenletből is látható, hogy a kinetikus energia négyzetesen függ a sebességtől, ami azt jelenti, hogy a sebesség kétszeresére növelése négyszeresére növeli a kinetikus energiát. A tömeggel pedig egyenesen arányos, tehát kétszer akkora tömeg kétszer akkora kinetikus energiát jelent azonos sebesség mellett.

Gondoljunk csak egy guruló labdára, egy repülő repülőgépre vagy egy futó emberre. Mindegyik rendelkezik kinetikus energiával a mozgásuk miatt. Minél gyorsabban mozognak, annál nagyobb ez az energia. A kinetikus energia kulcsszerepet játszik számos fizikai jelenség megértésében, a mikroszkopikus részecskék mozgásától kezdve a bolygók pályájáig.

A Potenciális Energia: A Helyzetből Származó Energia

A potenciális energia egy test helyzetéből vagy konfigurációjából származó tárolt energia. Többféle formája létezik, attól függően, hogy milyen erőhatás eredményezi ezt az energiát. A mechanikában leggyakrabban a gravitációs potenciális energiával és a rugalmas potenciális energiával találkozunk.

Gravitációs Potenciális Energia

A gravitációs potenciális energia egy testnek a gravitációs térben elfoglalt helyzetéből adódik. A Föld felszínén, egy \\mathbf\{h\} magasságban lévő \\mathbf\{m\} tömegű test gravitációs potenciális energiája (E\_p) a következőképpen számítható ki:

\\mathbf\{E\_p \= mgh\}

ahol \\mathbf\{g\} a gravitációs gyorsulás (a Földön megközelítőleg 9\.81 \\, m/s^2). Ebből az egyenletből láthatjuk, hogy minél magasabbra emelünk egy testet, annál nagyobb lesz a gravitációs potenciális energiája. Ez az energia akkor szabadul fel, amikor a test leesik, és a potenciális energia kinetikus energiává alakul át.

Például egy hegy tetején álló kő nagyobb gravitációs potenciális energiával rendelkezik, mint egy a völgyben fekvő kő. Amikor a kő legurul a hegyről, ez a potenciális energia fokozatosan kinetikus energiává alakul át, miközben a magassága csökken.

Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmasan deformálható testben (például egy megnyújtott rugóban vagy egy meghajlított íjban) tárolt energia. Ha egy rugót \\mathbf\{x\} távolsággal megnyújtunk vagy összenyomunk a nyugalmi helyzetéhez képest, a benne tárolt rugalmas potenciális energia (E\_\{pr\}) a következőképpen adható meg:

\\mathbf\{E\_\{pr\} \= \\frac\{1\}\{2\}kx^2\}

ahol \\mathbf\{k\} a rugóállandó, amely a rugó merevségét jellemzi. Minél nagyobb a rugóállandó vagy a deformáció mértéke, annál nagyobb a tárolt rugalmas potenciális energia.

Egy megfeszített íjban tárolt rugalmas potenciális energia például arra használható fel, hogy egy nyilat nagy sebességgel kilőjön. Amikor az íj elengedik, a rugalmas potenciális energia kinetikus energiává alakul át, ami a nyilat repíti.

A Mechanikai Energia Megmaradásának Törvénye: A Kimondás és Magyarázat

Most, hogy megértettük a kinetikus és a potenciális energia fogalmát, rátérhetünk a mechanikai energia megmaradásának törvényére. Ahogy korábban említettük, ez a törvény azt állítja, hogy egy olyan izolált rendszerben, amelyre csak konzervatív erők hatnak, a mechanikai energia (a kinetikus és potenciális energia összege) állandó marad.

Matematikailag ezt a következőképpen fejezhetjük ki:

\\mathbf\{E\_\{mech\} \= E\_k \+ E\_p \= állandó\}

Vagyis, ha egy rendszer kezdeti állapotában a kinetikus energia E\_\{k1\} és a potenciális energia E\_\{p1\}, a mechanikai energia E\_\{mech1\} \= E\_\{k1\} \+ E\_\{p1\}. Egy későbbi időpontban, ha a kinetikus energia E\_\{k2\} és a potenciális energia E\_\{p2\}, akkor a mechanikai energia E\_\{mech2\} \= E\_\{k2\} \+ E\_\{p2\}. A megmaradás törvénye szerint:

\\mathbf\{E\_\{mech1\} \= E\_\{mech2\}\}

\\mathbf\{E\_\{k1\} \+ E\_\{p1\} \= E\_\{k2\} \+ E\_\{p2\}\}

Ez az egyenlet rendkívül hasznos problémák megoldásában, ahol energiatranszformációk történnek, de nincsenek nem konzervatív erők, amelyek energiát vonhatnak el a rendszerből (például súrlódás vagy légellenállás).

Konzervatív Erők vs. Nem Konzervatív Erők

A mechanikai energia megmaradásának törvénye szigorúan csak olyan rendszerekre érvényes, ahol a ható erők konzervatívak. Fontos megérteni a különbséget a konzervatív és a nem konzervatív erők között.

Konzervatív Erők

Egy erő akkor konzervatív, ha az általa végzett munka egy zárt úton nulla, vagy ha a két pont közötti munka független az úttól. A mechanikában a leggyakoribb konzervatív erők a gravitációs erő és a rugalmas erő. Amikor egy konzervatív erő munkát végez egy rendszeren, az energia potenciális energiaként tárolódik, és később visszanyerhető kinetikus energiaként (vagy más formában).

• Gravitációs erő: A gravitációs erő által végzett munka egy test felemelésekor megegyezik a gravitációs potenciális energia növekedésével. Amikor a test leesik, ez a potenciális energia kinetikus energiává alakul vissza.
• Rugalmas erő: Egy rugó megnyújtásakor vagy összenyomásakor a rugalmas erő munkát végez, amely rugalmas potenciális energiaként tárolódik. Amikor a rugó visszatér nyugalmi helyzetébe, ez az energia kinetikus energiává alakulhat.

Nem Konzervatív Erők

Egy erő akkor nem konzervatív, ha az általa végzett munka függ az úttól, és nem nulla egy zárt úton. A mechanikában a leggyakoribb nem konzervatív erők a súrlódási erő és a légellenállás. Amikor egy nem konzervatív erő munkát végez, az energia általában hővé alakul, és nem tér vissza a rendszer mechanikai energiájába.

• Súrlódási erő: Ha egy test egy felületen csúszik, a súrlódási erő munkát végez, amely hővé alakítja a mechanikai energiát (mind a test, mind a felület felmelegszik). Ez az energia nem nyerhető vissza mechanikai munkaként a rendszerben.
• Légellenállás: Egy levegőben mozgó testre ható légellenállási erő szintén nem konzervatív. Munkája hővé alakítja a mechanikai energiát és a levegő áramlásának energiájává.

A mechanikai energia megmaradásának törvénye csak akkor alkalmazható közvetlenül, ha a rendszerben ható összes erő konzervatív. Ha nem konzervatív erők is jelen vannak, akkor a rendszer teljes energiája (beleértve a hőenergiát is) marad meg, de a mechanikai energia önmagában nem feltétlenül állandó.

Példák a Mechanikai Energia Megmaradására

Számos klasszikus példa illusztrálja a mechanikai energia megmaradásának törvényét a gyakorlatban. Nézzünk meg néhányat részletesen:

Egy Szabadon Eső Test

Képzeljünk el egy \\mathbf\{m\} tömegű testet, amelyet egy \\mathbf\{h\} magasságból elejtünk. Kezdetben a test nyugalomban van, így a kinetikus energiája nulla (E\_\{k1\} \= 0), a potenciális energiája pedig E\_\{p1\} \= mgh. Tehát a kezdeti mechanikai energia E\_\{mech1\} \= 0 \+ mgh \= mgh.

Amint a test esni kezd, a gravitációs erő munkát végez rajta, és a potenciális energiája csökken, miközben a sebessége és ezzel együtt a kinetikus energiája nő. Egy tetszőleges \\mathbf\{y\} magasságban (ahol 0 \\le y \\le h), a potenciális energia E\_\{p2\} \= mgy. A sebességet ebben a pontban a következőképpen számíthatjuk ki a mozgásegyenletekből:

v^2 \= v\_0^2 \+ 2a\(h\-y\)

Mivel a kezdeti sebesség v\_0 \= 0 és a gyorsulás a \= g, ezért:

v^2 \= 2g\(h\-y\)

Így a kinetikus energia ebben a pontban:

E\_\{k2\} \= \\frac\{1\}\{2\}mv^2 \= \\frac\{1\}\{2\}m\(2g\(h\-y\)\) \= mg\(h\-y\)

A mechanikai energia ezen a ponton tehát:

E\_\{mech2\} \= E\_\{k2\} \+ E\_\{p2\} \= mg\(h\-y\) \+ mgy \= mgh

Láthatjuk, hogy E\_\{mech1\} \= E\_\{mech2\} \= mgh, ami azt bizonyítja, hogy a mechanikai energia megmarad a szabadesés során (feltételezve, hogy a légellenállás elhanyagolható).

A földetérés pillanatában (y \= 0), a potenciális energia nulla (E\_\{p3\} \= 0), a kinetikus energia pedig:

E\_\{k3\} \= mg\(h\-0\) \= mgh

Így a mechanikai energia ekkor is E\_\{mech3\} \= mgh \+ 0 \= mgh. Az egész folyamat során a gravitációs potenciális energia folyamatosan kinetikus energiává alakul át, de a kettő összege (a mechanikai energia) állandó marad.

Egy Ideális Ingamozgása

Tekintsünk egy ideális ingát, amely egy \\mathbf\{L\} hosszúságú, súlytalan fonálon függő \\mathbf\{m\} tömegű testből áll, és súrlódás nélkül leng. Amikor az inga a legmagasabb pontján van (valamelyik szélső helyzetben), pillanatnyi sebessége nulla, így a kinetikus energiája is nulla. Ebben a pontban a gravitációs potenciális energiája maximális, a legalacsonyabb ponthoz (egyensúlyi helyzethez) viszonyít