Helyzeti Energia Kiszamitasa

A Helyzeti Energia Kiszámítása: A Potenciális Energia Részletes Megközelítése

A helyzeti energia, más néven potenciális energia, a fizikában egy test vagy rendszer energiájának azon összetevője, amely a test vagy a rendszer helyzetéből vagy konfigurációjából adódik. Ez az energia tárolt formában van jelen, és képes munkát végezni, ha a rendszer megváltoztatja a helyzetét vagy konfigurációját. A helyzeti energia kulcsfontosságú fogalom a mechanikában, az elektromágnességben és más fizikai területeken is. Ebben a részletes útmutatóban mélyrehatóan megvizsgáljuk a helyzeti energia fogalmát, a különböző típusait, a kiszámításának módjait, valamint a gyakorlati alkalmazásait.

A Helyzeti Energia Alapjai

Ahhoz, hogy megértsük a helyzeti energia kiszámítását, először tisztáznunk kell magát a fogalmat. A potenciális energia egy olyan energiaforma, amely egy objektum vagy rendszer relatív helyzetéből, elrendezéséből vagy állapotából származik. Nem mozgással, hanem a potenciállal van összefüggésben, hogy mozgást hozzon létre. Gondoljunk egy magasban tartott kőre: amíg tartjuk, nem mozog, de rendelkezik potenciális energiával, amely felszabadul, ha elengedjük, és a gravitáció hatására leesik.

A Potenciális Energia Különböző Típusai

A potenciális energiának többféle formája létezik, amelyek különböző kölcsönhatásokhoz kapcsolódnak. A leggyakrabban előforduló típusok a következők:

Gravitációs Potenciális Energia

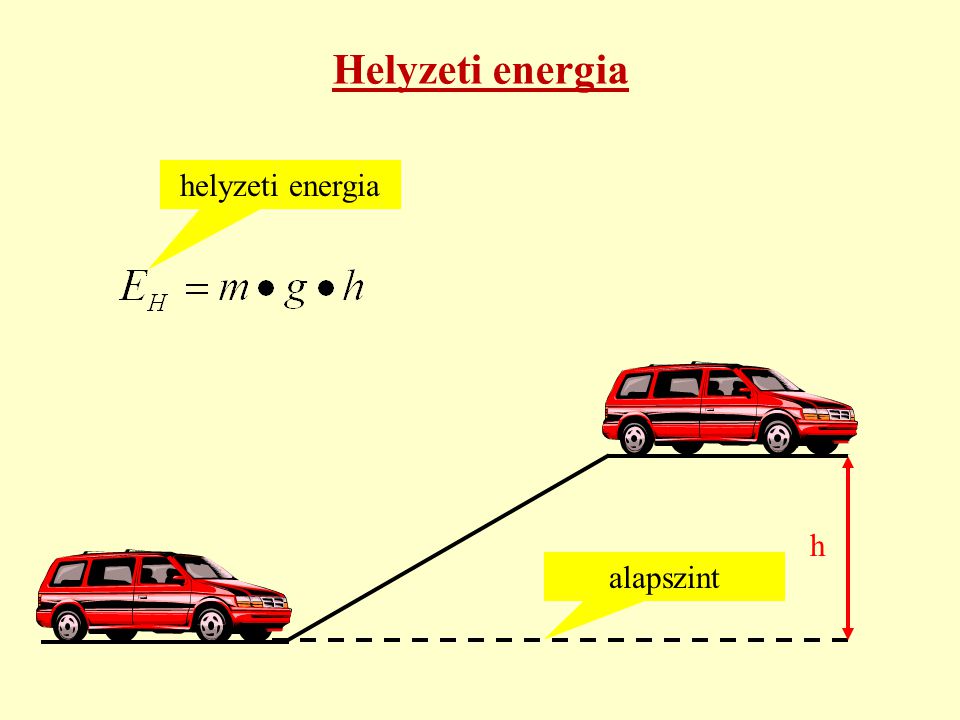
A gravitációs potenciális energia egy objektum tömegéből és a gravitációs mezőben elfoglalt helyzetéből adódik. Minél magasabban van egy objektum a Föld felszínéhez képest (vagy egy másik gravitációs testhez képest), annál nagyobb a gravitációs potenciális energiája. A gravitációs potenciális energia kiszámításának képlete a következő:

\\Large E\_p \= mgh

ahol:

• \(E_p\) a gravitációs potenciális energia (joule-ban mérve)
• \(m\) az objektum tömege (kilogrammban mérve)
• \(g\) a gravitációs gyorsulás (a Földön körülbelül \(9.81 \, m/s^2\))
• \(h\) az objektum magassága egy referencia szinthez képest (méterben mérve)

A referencia szint megválasztása önkényes, de a számítások szempontjából konzisztensnek kell lennie. Gyakran a Föld felszínét választják referencia szintnek, ahol a magasság \(h=0\), és így a potenciális energia is nulla.

Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmasan deformálható objektumban (például egy rugóban vagy egy gumiszalagban) tárolt energia, amelyet az objektum alakjának megváltoztatása okoz. Ha egy rugót megnyújtunk vagy összenyomunk, munkát végzünk rajta, és ez a munka rugalmas potenciális energiaként tárolódik. A rugalmas potenciális energia kiszámításának képlete a Hooke-törvényen alapul:

\\Large E\_p \= \\frac\{1\}\{2\}kx^2

ahol:

• \(E_p\) a rugalmas potenciális energia (joule-ban mérve)
• \(k\) a rugóállandó (newton per méterben mérve), amely a rugó merevségét jellemzi

• \(x\) a rugó egyensúlyi helyzetétől való elmozdulás (méterben mérve)

Minél nagyobb a rugóállandó vagy az elmozdulás, annál nagyobb a tárolt rugalmas potenciális energia.

Elektromos Potenciális Energia

Az elektromos potenciális energia elektromos töltések rendszerében tárolt energia, amely a töltések egymáshoz viszonyított helyzetéből adódik. Két azonos előjelű töltés közelebb hozása növeli az elektromos potenciális energiát, mivel munkát kell végeznünk a taszítóerő ellenében. Két ellentétes előjelű töltés közelebb hozása csökkenti az elektromos potenciális energiát, mivel a vonzóerő munkát végez.

Két ponttöltés \(q_1\) és \(q_2\) elektromos potenciális energiája \(r\) távolságban a következőképpen számítható:

\\Large E\_p \= k\_e \\frac\{q\_1 q\_2\}\{r\}

ahol \(k_e\) a Coulomb-állandó (\(8.9875 \times 10^9 \, N \cdot m^2/C^2\)).

Mágneses Potenciális Energia

A mágneses potenciális energia mágneses mezőben elhelyezkedő mágneses dipólus energiája. Például egy iránytű tűjének mágneses potenciális energiája függ a Föld mágneses mezőjéhez viszonyított orientációjától. A mágneses potenciális energia bonyolultabb képletekkel írható le, amelyek figyelembe veszik a mágneses momentumot és a mágneses mező erősségét.

Kémiai Potenciális Energia

A kémiai potenciális energia az atomok és molekulák közötti kémiai kötésekben tárolt energia. Ez az energia szabadul fel kémiai reakciók során, például égéskor vagy emésztéskor. Bár nem közvetlenül a helyzettel kapcsolatos a makroszkopikus értelemben, mégis potenciális energiának tekintjük, mivel a részecskék konfigurációjában rejlik.

Nukleáris Potenciális Energia

A nukleáris potenciális energia az atommagban lévő nukleonok (protonok és neutronok) közötti kölcsönhatásokból származik. Ez az energia szabadul fel nukleáris reakciók során, például a maghasadáskor vagy a magfúziókor. Hatalmas mennyiségű energia tárolható ebben a formában.

A Gravitációs Helyzeti Energia Részletes Kiszámítása

Mivel a “helyzeti energia kiszámítása” kifejezés a köznapi nyelvben leggyakrabban a gravitációs potenciális energiára utal, most ezt a típust fogjuk részletesebben megvizsgálni.

A Képlet Értelmezése

A gravitációs potenciális energia képlete, \(E_p = mgh\), egyszerű, de mély jelentéssel bír. A képlet azt mutatja, hogy a potenciális energia egyenesen arányos a test tömegével (\(m\)), a gravitációs gyorsulással (\(g\)), és a referencia szinthez viszonyított magasságával (\(h\)).

Tömeg (\(m\))

A tömeg az anyag mennyiségének mértéke egy objektumban. Minél nagyobb egy objektum tömege, annál nagyobb a gravitációs erő, amely hat rá, és annál nagyobb a potenciális energiája egy adott magasságban.

Gravitációs Gyorsulás (\(g\))

A gravitációs gyorsulás a gravitációs tér által egy objektumra kifejtett gyorsulás. A Föld felszínén ez az érték átlagosan \(9.81 \, m/s^2\). Más égitesteken (például a Holdon vagy a Marson) a gravitációs gyorsulás eltérő.

Magasság (\(h\))

A magasság az objektum vertikális távolsága egy kiválasztott referencia szinthez képest. A referencia szint lehet a Föld felszíne, egy épület alapja, vagy bármilyen más kényelmes pont. Fontos, hogy a számítás során következetesen ugyanazt a referencia szintet használjuk.

Példák a Gravitációs Potenciális Energia Kiszámítására

Nézzünk néhány példát a gravitációs potenciális energia kiszámítására, hogy jobban megértsük a képlet alkalmazását.

1. példa: Egy leeső alma

Egy \(0.2 \, kg\) tömegű alma egy \(3 \, m\) magas faágról esik le. Mennyi volt az alma gravitációs potenciális energiája, mielőtt leesett (a Föld felszínéhez képest)?

Adatok:

• Tömeg (\(m\)) = \(0.2 \, kg\)
• Magasság (\(h\)) = \(3 \, m\)
• Gravitációs gyorsulás (\(g\)) = \(9.81 \, m/s^2\)

A képletet alkalmazva:

\\Large E\_p \= mgh \= \(0\.2 \\, kg\) \\times \(9\.81 \\, m/s^2\) \\times \(3 \\, m\) \= 5\.886 \\, J

Tehát az alma gravitációs potenciális energiája a faágon \(5.886 \, joule\) volt.

2. példa: Egy hegy tetején lévő turista

Egy \(70 \, kg\) tömegű turista egy \(1500 \, m\) magas hegy tetején áll. Mennyi a turista gravitációs potenciális energiája a tengerszinthez képest?

Adatok:

• Tömeg (\(m\)) = \(70 \, kg\)
• Magasság (\(h\)) = \(1500 \, m\)
• Gravitációs gyorsulás (\(g\)) = \(9.81 \, m/s^2\)

A képletet alkalmazva:

\\Large E\_p \= mgh \= \(70 \\, kg\) \\times \(9\.81 \\, m/s^2\) \\times \(1500 \\, m\) \= 1,030,050 \\, J \= 1030\.05 \\, kJ

A turista gravitációs potenciális energiája a tengerszinthez képest körülbelül \(1030.05 \, kilojoule\).

3. példa: Egy repülőgép

Egy \(50,000 \, kg\) tömegű repülőgép \(10,000 \, m\) magasan repül a tengerszint felett. Számítsuk ki a repülőgép gravitációs potenciális energiáját.

Adatok:

• Tömeg (\(m\)) = \(50,000 \, kg\)
• Magasság (\(h\)) = \(10,000 \, m\)
• Gravitációs gyorsulás (\(g\)) = \(9.81 \, m/s^2\)

A képletet alkalmazva:

\\Large E\_p \= mgh \= \(50,000 \\, kg\) \\times \(9\.81 \\, m/s^2\) \\times \(10,000 \\, m\) \= 4,905,000,000 \\, J \= 4\.905 \\, GJ

A repülőgép gravitációs potenciális energiája \(4.905 \, gigajoule\>.

A Referencia Szint Fontossága

Fontos megjegyezni, hogy a gravitációs potenciális energia értéke függ a választott referencia szinttől. Ha egy másik referencia szintet választunk, a magasság (\(h\)) értéke megváltozik, és így a potenciális energia értéke is. Azonban a potenciális energia különbsége két pont között független a referencia szint megválasztásától. Például, ha egy objektum \(h_1\) magasságból \(h_2\) magasságba esik, a potenciális energia változása \(mg(h_2 – h_1)\), ami nem függ attól, hogy a \(h=0\) szintet hol vettük fel.

A Rugalmas Helyzeti Energia Részletes Kiszámítása

Most nézzük meg a rugalmas potenciális energia kiszámítását részletesebben.

A Képlet Értelmezése

A rugalmas potenciális energia képlete, \(E_p = \frac{1}{2}kx^2\), azt mutatja, hogy a tárolt energia arányos a rugóállandóval (\(k\)) és az elmozdulás négyzetével (\(x^2\)).

Rugóállandó (\(k\))

A rugóállandó (\(k\)) a rugó merevségének mértéke. Nagyobb \(k\) érték merevebb rugót jelent, amelyhez nagyobb erő szükséges az azonos mértékű megnyújtáshoz vagy összenyomáshoz. A rugóállandót általában newton per méter (\(N/m\)) egységben mérik.

Elmozdulás (\(x\))

Az elmozdulás (\(x\)) a rugó egyensúlyi helyzetétől való távolságot jelenti. Ez lehet megnyúlás vagy összenyomás. A potenciális energia az elmozdulás négyzetével arányos, ami azt jelenti, hogy az elmozdulás kétszeresére növelése négyszeresére növeli a tárolt energiát.

Példák a Rugalmas Potenciális Energia Kiszámítására

Nézzünk néhány példát a rugalmas potenciális energia kiszámítására.

1. példa: Megnyújtott rugó

Egy rugó rugóállandója \(k = 100 \, N/m\). Mennyi a rugalmas potenciális energia, ha a rugót \(0.1 \, m\)-rel megnyújtjuk?

Adatok:

• Rugóállandó (\(k\)) = \(100 \, N/m\)
• Elmozdulás (\(x\)) = \(0.1 \, m\)

A képletet alkalmazva:

\\Large E\_p \= \\frac\{1\}\{2\}kx^2 \= \\frac\{1\}\{2\} \\times \(100 \\, N/m\) \\times \(0\.1 \\, m\)^2 \= \\frac\{1\}\{2\} \\times 100 \\times 0\.01 \\, J \= 0\.5 \\, J

A rugalmas potenciális energia \(0.5 \, joule

Mechanikai Energia Feladatok

Mechanikai Energia Feladatok: Átfogó Gyakorlatok és Megoldások a Sikeres Tanuláshoz

Üdvözöljük a mechanikai energia világában! Ez az átfogó útmutató részletes feladatokon keresztül segít elmélyíteni a kinetikus energia, a potenciális energia, a munka fogalmát és az energiamegmaradás törvényét. Célunk, hogy a legbonyolultabbnak tűnő feladatokat is érthetővé és megoldhatóvá tegyük. Készüljön fel, hogy elsajátítsa a mechanikai energia alapelveit!

A Mechanikai Energia Alapjai: Kinetikus és Potenciális Energia

A mechanikai energia egy rendszer mozgásával vagy helyzetével kapcsolatos energia. Két fő formája létezik: a kinetikus energia, amely a mozgásból származik, és a potenciális energia, amely a test helyzetéből vagy konfigurációjából adódik. Mindkét fogalom kulcsfontosságú a fizikai problémák megértéséhez és megoldásához.

Kinetikus Energia: A Mozgás Energiája

A kinetikus energia (\\\(E\_k\\\)) egy test mozgásának köszönhető energia. Minél nagyobb egy test tömege és sebessége, annál nagyobb a kinetikus energiája. A kinetikus energia képlete a következő:

\\\(E\_k \= \\frac\{1\}\{2\}mv^2\\\)

ahol \\\(m\\\) a test tömege (kilogrammban), és \\\(v\\\) a test sebessége (méter per szekundumban). A kinetikus energia mértékegysége a joule (J).

Gyakorló Feladatok a Kinetikus Energiához

1. Egy 2 kg tömegű test 5 m/s sebességgel mozog. Mekkora a kinetikus energiája?
2. Egy autó kinetikus energiája 100 kJ, tömege 1000 kg. Mekkora a sebessége?
3. Hasonlítsa össze egy 1 kg-os, 10 m/s sebességgel mozgó test és egy 2 kg-os, 5 m/s sebességgel mozgó test kinetikus energiáját.

Megoldások a Kinetikus Energia Feladataihoz

1. \\\(E\_k \= \\frac\{1\}\{2\} \\times 2 \\text\{ kg\} \\times \(5 \\text\{ m/s\}\)^2 \= 1 \\text\{ kg\} \\times 25 \\text\{ m\}^2/\\text\{s\}^2 \= 25 \\text\{ J\}\\\)
2. \\\(100 \\times 10^3 \\text\{ J\} \= \\frac\{1\}\{2\} \\times 1000 \\text\{ kg\} \\times v^2\\\). Ebből \\\(v^2 \= \\frac\{2 \\times 100 \\times 10^3\}\{1000\} \= 200 \\text\{ m\}^2/\\text\{s\}^2\\\), tehát \\\(v \= \\sqrt\{200\} \\approx 14\.14 \\text\{ m/s\}\\\).
3. Az első test kinetikus energiája: \\\(E\_\{k1\} \= \\frac\{1\}\{2\} \\times 1 \\text\{ kg\} \\times \(10 \\text\{ m/s\}\)^2 \= 50 \\text\{ J\}\\\). A második test kinetikus energiája: \\\(E\_\{k2\} \= \\frac\{1\}\{2\} \\times 2 \\text\{ kg\} \\times \(5 \\text\{ m/s\}\)^2 \= 25 \\text\{ J\}\\\). Tehát az első test kinetikus energiája kétszer akkora.

Potenciális Energia: A Helyzetből Származó Energia

A potenciális energia (\\\(E\_p\\\)) egy test helyzetéből vagy konfigurációjából adódó energia. A leggyakrabban tárgyalt potenciális energiafajták a gravitációs potenciális energia és a rugalmas potenciális energia.

Gravitációs Potenciális Energia

A gravitációs potenciális energia egy test magasságától függ a gravitációs térben. A Föld felszínéhez közeli gravitációs potenciális energia képlete:

\\\(E\_p \= mgh\\\)

ahol \\\(m\\\) a test tömege, \\\(g\\\) a gravitációs gyorsulás (kb. \\\(9\.81 \\text\{ m/s\}^2\\\) a Földön), és \\\(h\\\) a test magassága egy referencia szinthez képest.

Gyakorló Feladatok a Gravitációs Potenciális Energiához

1. Egy 0.5 kg tömegű labdát 10 m magasra emelünk. Mekkora a gravitációs potenciális energiája a talajhoz képest?
2. Egy 50 kg tömegű személy egy 30 m magas épület tetején áll. Mekkora a gravitációs potenciális energiája a talajszinthez viszonyítva?
3. Egy 2 kg-os könyv egy polcon van, amely a talajtól 1.5 m magasan található. Mekkora a könyv gravitációs potenciális energiája?

Megoldások a Gravitációs Potenciális Energia Feladataihoz

1. \\\(E\_p \= 0\.5 \\text\{ kg\} \\times 9\.81 \\text\{ m/s\}^2 \\times 10 \\text\{ m\} \= 49\.05 \\text\{ J\}\\\)

2. \\\(E\_p \= 50 \\text\{ kg\} \\times 9\.81 \\text\{ m/s\}^2 \\times 30 \\text\{ m\} \= 14715 \\text\{ J\}\\\)
3. \\\(E\_p \= 2 \\text\{ kg\} \\times 9\.81 \\text\{ m/s\}^2 \\times 1\.5 \\text\{ m\} \= 29\.43 \\text\{ J\}\\\)

Rugalmas Potenciális Energia

A rugalmas potenciális energia egy rugalmasan deformált testben tárolt energia, például egy megnyújtott vagy összenyomott rugóban. A rugalmas potenciális energia képlete:

\\\(E\_p \= \\frac\{1\}\{2\}kx^2\\\)

ahol \\\(k\\\) a rugóállandó (N/m), és \\\(x\\\) a rugó egyensúlyi helyzetétől való elmozdulása (méterben).

Gyakorló Feladatok a Rugalmas Potenciális Energiához

1. Egy rugó rugóállandója 100 N/m. Mekkora a rugalmas potenciális energia, ha a rugót 0.1 m-rel megnyújtjuk?
2. Egy rugalmas katapultot 0.2 m-rel húzunk hátra. A rugóállandó 500 N/m. Mekkora a tárolt rugalmas potenciális energia?
3. Egy rugóban 10 J rugalmas potenciális energia tárolódik, amikor 0.5 m-rel van összenyomva. Mekkora a rugóállandó?

Megoldások a Rugalmas Potenciális Energia Feladataihoz

1. \\\(E\_p \= \\frac\{1\}\{2\} \\times 100 \\text\{ N/m\} \\times \(0\.1 \\text\{ m\}\)^2 \= 0\.5 \\times 100 \\times 0\.01 \\text\{ J\} \= 0\.5 \\text\{ J\}\\\)
2. \\\(E\_p \= \\frac\{1\}\{2\} \\times 500 \\text\{ N/m\} \\times \(0\.2 \\text\{ m\}\)^2 \= 0\.5 \\times 500 \\times 0\.04 \\text\{ J\} \= 10 \\text\{ J\}\\\)
3. \\\(10 \\text\{ J\} \= \\frac\{1\}\{2\} \\times k \\times \(0\.5 \\text\{ m\}\)^2\\\). Ebből \\\(k \= \\frac\{2 \\times 10\}\{0\.25\} \= 80 \\text\{ N/m\}\\\).

A Munka és az Energia Kapcsolata: A Munkatétel

A munka (\\\(W\\\)) az az energia, amely egy testre ható erő hatására megváltozik. Ha egy erő elmozdít egy testet, akkor munkát végez az erő. A munka képlete:

\\\(W \= Fd\\cos\(\\theta\)\\\)

ahol \\\(F\\\) az erő nagysága, \\\(d\\\) az elmozdulás nagysága, és \\\(\\theta\\\) az erő és az elmozdulás közötti szög.

A Munkatétel: A Munka és a Kinetikus Energia Változása

A munkatétel kimondja, hogy egy testre ható összes munka egyenlő a test kinetikus energiájának megváltozásával:

\\\(W\_\{összes\} \= \\Delta E\_k \= E\_\{k,végső\} \- E\_\{k,kezdeti\}\\\)

Gyakorló Feladatok a Munkatételhez

1. Egy 10 kg tömegű test kezdetben nyugalomban van. Egy 20 N-os vízszintes erő hat rá 5 méteren keresztül. Mekkora a test végső kinetikus energiája és sebessége?
2. Egy autó sebessége 20 m/s-ról 30 m/s-ra nő, miközben 500 m-en keresztül gyorsul. A tömege 1500 kg. Mekkora a motor által végzett munka?
3. Egy labdát függőlegesen felfelé dobunk. Kezdeti kinetikus energiája 100 J. A legmagasabb ponton a kinetikus energiája 0 J. Mekkora munkát végzett a gravitációs erő?

Megoldások a Munkatétel Feladataihoz

1. A végzett munka: \\\(W \= Fd \= 20 \\text\{ N\} \\times 5 \\text\{ m\} \= 100 \\text\{ J\}\\\). A munkatétel szerint \\\(\\Delta E\_k \= W\\\), így \\\(E\_\{k,végső\} \- 0 \= 100 \\text\{ J\}\\\), tehát \\\(E\_\{k,végső\} \= 100 \\text\{ J\}\\\). A végső sebességből: \\\(100 \\text\{ J\} \= \\frac\{1\}\{2\} \\times 10 \\text\{ kg\} \\times v^2\\\), \\\(v^2 \= 20 \\text\{ m\}^2/\\text\{s\}^2\\\), \\\(v \= \\sqrt\{20\} \\approx 4\.47 \\text\{ m/s\}\\\).
2. A kezdeti kinetikus energia: \\\(E\_\{k,kezdeti\} \= \\frac\{1\}\{2\} \\times 1500 \\text\{ kg\} \\times \(20 \\text\{ m/s\}\)^2 \= 300000 \\text\{ J\} \= 300 \\text\{ kJ\}\\\). A végső kinetikus energia: \\\(E\_\{k,végső\} \= \\frac\{1\}\{2\} \\times 1500 \\text\{ kg\} \\times \(30 \\text\{ m/s\}\)^2 \= 675000 \\text\{ J\} \= 675 \\text\{ kJ\}\\\). A végzett munka: \\\(W \= \\Delta E\_k \= 675 \\text\{ kJ\} \- 300 \\text\{ kJ\} \= 375 \\text\{ kJ\}\\\).
3. A gravitációs erő lefelé hat, az elmozdulás felfelé. A végzett munka \\\(W \= \\Delta E\_k \= 0 \- 100 \\text\{ J\} \= \-100 \\text\{ J\}\\\). A negatív előjel azt jelzi, hogy a gravitációs erő a mozgás ellenében végez munkát.

Az Energiamegmaradás Törvénye

Az energiamegmaradás törvénye az egyik legalapvetőbb fizikai törvény. Kimondja, hogy egy zárt rendszer teljes energiája állandó marad, bár az energia egyik formájából a másikba alakulhat át. Mechanikai rendszerekben ez azt jelenti, hogy a kinetikus és potenciális energia összege állandó, ha csak konzervatív erők (mint a gravitáció és a rugóerő) végeznek munkát.

\\\(E\_\{mechanikai\} \= E\_k \+ E\_p \= állandó\\\)

Feladatok az Energiamegmaradás Törvényéhez

1. Egy 1 kg tömegű labdát 20 m magasról elejtünk. Mekkora a sebessége, amikor eléri a talajt (elhanyagolva a légellenállást)?
2. Egy 0.2 kg tömegű golyót egy rugó segítségével lőnek ki vízszintesen. A rugóállandó 500 N/m, és a rugót 0.1 m-rel nyomták össze. Mekkora a golyó kilövési sebessége?
3. Egy hullámvasút kocsija egy 40 m magas pontról indul ki nyugalomban. Mekkora a sebessége egy 10 m magas ponton (elhanyagolva a súrlódást)?

Megoldások az Energiamegmaradás Törvénye Feladataihoz

1. A kezdeti mechanikai energia (a legmagasabb ponton): \\\(E\_\{kezdeti\} \= E\_\{k,kezdeti\} \+ E\_\{p,kezdeti\} \= 0 \+ mgh \= 1 \\text\{ kg\} \\times 9\.81 \\text\{ m/s\}^2 \\times 20 \\text\{ m\} \= 196\.2 \\text\{ J\}\\\). A talajon a potenciális energia nulla