Katalizator Fogalma

A Katalizátor Fogalma: Átfogó Magyarázat és Alkalmazások

A kémia és a technológia világában a katalizátorok központi szerepet töltenek be. Ezek az anyagok anélkül képesek felgyorsítani a kémiai reakciókat, hogy maguk maradandó kémiai változáson mennének keresztül. Ez a rendkívüli tulajdonság teszi őket nélkülözhetetlenné számos ipari folyamatban, a gyógyszergyártástól kezdve a műanyagok előállításán át a környezetvédelmi technológiákig. Ebben a részletes cikkben mélyrehatóan feltárjuk a katalizátorok fogalmát, működési elvüket, különböző típusaikat és a legfontosabb alkalmazási területeiket.

Mi is pontosan a katalizátor?

A katalizátor definíció szerint olyan anyag, amely megnöveli egy kémiai reakció sebességét anélkül, hogy a reakció végén elfogyna. A katalizátor részt vesz a reakció mechanizmusában, de a nettó reakcióegyenletben nem szerepel. Ez azt jelenti, hogy a reakció végén a katalizátor kémiai összetétele nem változik meg. A katalizátorok kis mennyiségben is hatékonyak lehetnek, és gyakran szelektívek, ami azt jelenti, hogy egy adott katalizátor előnyben részesíthet egy bizonyos reakciót a többi lehetséges reakcióval szemben.

A katalízis alapelvei

A katalízis az a folyamat, amelynek során egy katalizátor felgyorsít egy kémiai reakciót. A katalizátor ezt úgy éri el, hogy egy alternatív reakcióutat kínál alacsonyabb aktiválási energiával. Az aktiválási energia az a minimális energia, amely szükséges ahhoz, hogy a reaktánsok termékké alakuljanak. A katalizátor jelenlétében kevesebb energiára van szükség a reakció beindulásához, ami azt eredményezi, hogy a reakció sokkal gyorsabban megy végbe adott hőmérsékleten.

Az aktiválási energia csökkentése

Képzeljünk el egy hegyet, amely elválasztja a reaktánsokat a termékektől. Az aktiválási energia ennek a hegynek a magassága. A katalizátor úgy működik, mintha egy alagutat fúrna ezen a hegyen keresztül, így a reaktánsoknak kevesebb energiára van szükségük ahhoz, hogy a termékekhez jussanak. Ez a megközelítés nem befolyásolja a reakció termodinamikáját, vagyis nem változtatja meg a reakció egyensúlyi helyzetét, csupán azt, hogy milyen gyorsan éri el a rendszer ezt az egyensúlyt.

A reakció mechanizmusa katalizátor jelenlétében

A katalizátor gyakran úgy működik, hogy átmeneti komplexeket képez a reaktánsokkal. Ezek a komplexek könnyebben alakulnak termékekké, majd a katalizátor felszabadul, hogy egy újabb reakcióciklust indítson el. A reakció mechanizmusa katalizátor jelenlétében tehát eltér a katalizátor nélküli reakcióétól.

Példa egy egyszerű katalitikus reakcióra

Vegyük példaként a hidrogén-peroxid ($\mathbf{H_2O_2}$) bomlását vízre ($\mathbf{H_2O}$) és oxigénre ($\mathbf{O_2}$). Ez a reakció lassan megy végbe magától, de mangán-dioxid ($\mathbf{MnO_2}$) jelenlétében sokkal gyorsabbá válik. A mangán-dioxid itt katalizátorként működik, anélkül, hogy elfogyna a reakció végén.

A katalizátorok főbb típusai

A katalizátorokat többféleképpen lehet csoportosítani, például a fázisuk (homogén vagy heterogén), a kémiai összetételük vagy a működési mechanizmusuk alapján.

Homogén katalizátorok

A homogén katalizátorok ugyanabban a fázisban vannak jelen, mint a reaktánsok. Ez általában folyadékfázist jelent. A homogén katalízis gyakran nagy szelektivitást és enyhe reakciókörülményeket tesz lehetővé.

Példák homogén katalizátorokra

• Savak és bázisok: Számos szerves kémiai reakciót katalizálnak, például észterezést vagy hidrolízist.
• Átmenetifém-komplexek: Széles körben alkalmazzák őket polimerizációs reakciókban, hidrogénezésben és más szerves átalakításokban. Például a Wilkinson-katalizátor (egy ródiumkomplex) olefinek hidrogénezésére használatos.

Heterogén katalizátorok

A heterogén katalizátorok más fázisban vannak jelen, mint a reaktánsok. Általában szilárdak, míg a reaktánsok gázok vagy folyadékok. A heterogén katalízis az ipari folyamatok nagy részében dominál, mivel a katalizátor könnyen elválasztható a reakcióelegytől.

A heterogén katalízis lépései

1. A reaktánsok diffúziója a katalizátor felületére.

2. A reaktánsok adszorpciója (megkötődése) a katalizátor aktív helyein.
3. A kémiai reakció végbemenetele az adszorbeált reaktánsok között a katalizátor felületén.
4. A termékek deszorpciója (leválása) a katalizátor felületéről.
5. A termékek diffúziója a katalizátor felületéről a bulk fázisba.

Példák heterogén katalizátorokra

• Fémek: Platina, palládium, nikkel, gyakran finoman eloszlatva egy hordozón (pl. alumínium-oxid, szilícium-dioxid). Alkalmazzák hidrogénezésre, dehidrogénezésre és oxidációra.
• Fém-oxidok: Például a vanádium(V)-oxid ($\mathbf{V_2O_5}$) a kén-dioxid kén-trioxiddá történő oxidációjában a kénsavgyártás során.
• Zeolitok: Porózus alumínium-szilikátok, amelyeket krakkolásra, izomerizációra és más petrolkémiai folyamatokra használnak.

Enzimek: Biológiai katalizátorok

Az enzimek a természet csodálatos katalizátorai. Ezek nagyméretű fehérjemolekulák, amelyek rendkívül specifikusak egy-egy biokémiai reakcióra. Az enzimek sokkal hatékonyabbak, mint a legtöbb mesterséges katalizátor, és a reakciókat enyhe körülmények között (testhőmérséklet, atmoszférikus nyomás) katalizálják.

Az enzimek működési mechanizmusa

Az enzimek aktív központtal rendelkeznek, amely egy specifikus alakú üreg, ahová a szubsztrát (a reakcióba lépő molekula) kötődik. Az enzim-szubsztrát komplex kialakulása csökkenti a reakció aktiválási energiáját, lehetővé téve a gyorsabb reakciót. A termék(ek) felszabadulása után az enzim visszanyeri eredeti formáját, és készen áll egy újabb szubsztrát megkötésére.

A katalizátorok jelentősége az iparban

A katalizátorok nélkülözhetetlenek a modern vegyipar számára. Számos nagytömegű vegyi anyag, például ammónia, salétromsav, kénsav és polimerek gyártása katalitikus folyamatokon alapul. A katalizátorok alkalmazása lehetővé teszi a reakciók gyorsabb végbemenetelét, alacsonyabb hőmérsékleten és nyomáson, ami csökkenti az energiafelhasználást és a költségeket.

Fontos ipari katalitikus eljárások

• Haber-Bosch eljárás: A nitrogén és a hidrogén ammóniává történő katalitikus egyesítése (vas-oxid katalizátor).
• Ostwald-eljárás: Az ammónia salétromsavatá történő oxidációja (platina-ródium háló katalizátor).
• Kontakteljárás: A kén-dioxid kén-trioxiddá történő oxidációja (vanádium(V)-oxid katalizátor), a kénsavgyártás kulcslépése.
• Kőolaj-finomítás: Számos katalitikus folyamatot alkalmaznak a kőolaj frakcionálására és a kívánt szénhidrogének előállítására (pl. zeolitok a krakkolásban, platina-alumínium a reformálásban).
• Polimerizáció: Számos polimer (pl. polietilén, polipropilén) gyártása fémorganikus katalizátorok (pl. Ziegler-Natta katalizátorok) segítségével történik.

A katalizátorok szerepe a környezetvédelemben

A katalizátorok a környezetvédelmi technológiákban is kulcsfontosságúak. Segítenek csökkenteni a káros kibocsátásokat és tisztítani a szennyezett levegőt és vizet.

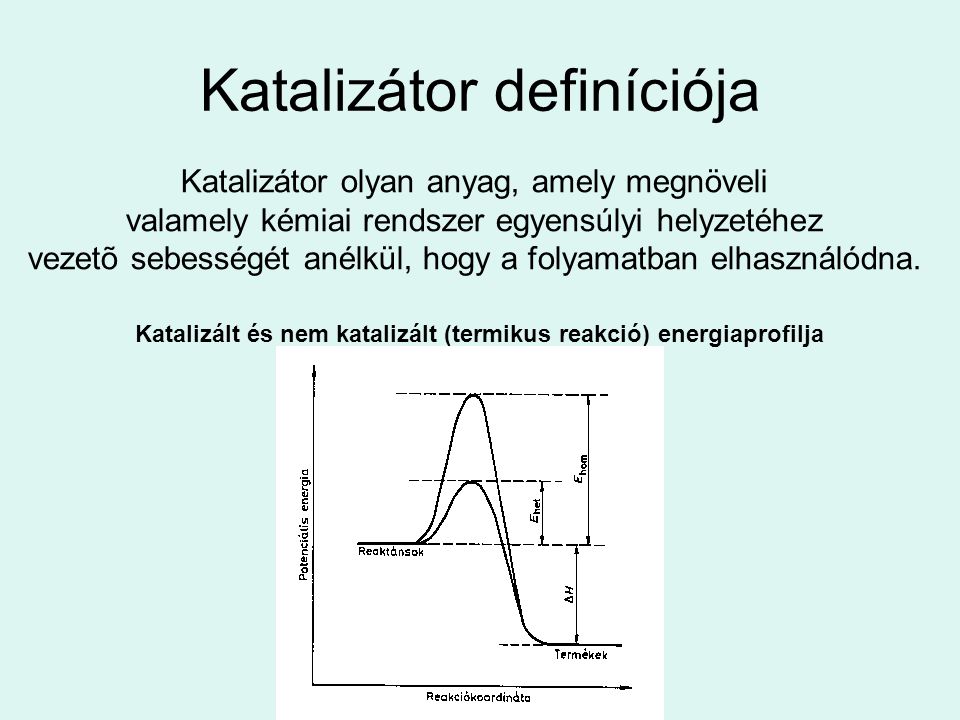
Autókatalizátorok

Az autókatalizátorok a gépjárművek kipufogógázában található káros anyagokat (szén-monoxid, nitrogén-oxidok, szénhidrogének) kevésbé káros anyagokká (szén-dioxid, nitrogén, víz) alakítják át. A modern autók háromutas katalizátort használnak, amely egyszerre oxidálja a szénhidrogéneket és a szén-monoxidot, valamint redukálja a nitrogén-oxidokat.

Ipari kibocsátás kezelése

A katalizátorokat az ipari létesítmények kibocsátásának kezelésére is alkalmazzák. Például a denitrifikációs katalizátorok a nitrogén-oxidokat nitrogénné alakítják, míg az oxidációs katalizátorok a szerves szennyezőket szén-dioxiddá és vízzé oxidálják.

A katalizátorok fejlesztésének jövőbeli irányai

A katalizátorok kutatása és fejlesztése folyamatosan zajlik. A cél új, hatékonyabb, szelektívebb és környezetbarátabb katalizátorok kifejlesztése. A nanotechnológia, a számítógépes modellezés és a fejlett analitikai technikák mind hozzájárulnak ehhez a folyamathoz.

Fókuszban a fenntarthatóság

A jövőbeli katalizátorok fejlesztésének egyik kulcsfontosságú szempontja a fenntarthatóság. Ez magában foglalja a ritka és drága nemesfémek helyettesítését olcsóbb és bőségesebben előforduló anyagokkal, valamint a katalizátorok élettartamának növelését és az újrahasznosításukra való törekvést.

Szelektív katalízis

Egy másik fontos irány a magas szelektivitású katalizátorok kifejlesztése. Ez lehetővé teszi, hogy egy adott reakciót szinte kizárólagosan vigyenek végbe, minimalizálva a nem kívánt melléktermékek képződését, ami egyszerűsíti a termék tisztítását és csökkenti a hulladék mennyiségét.

Összefoglalás

A katalizátorok olyan anyagok, amelyek felgyorsítják a kémiai reakciókat anélkül, hogy maguk elfogynának. Két fő típusuk létezik: a homogén és a heterogén katalizátorok. A biológiai rendszerekben az enzimek töltik be a katalizátor szerepét. A katalizátorok nélkülözhetetlenek a modern iparban és a környezetvédelemben. A kutatás és fejlesztés folyamatosan új, hatékonyabb és fenntarthatóbb katalizátorok létrehozására irányul.

További információk és források

Ha mélyebben szeretne elmerülni a katalizátorok világában, javasoljuk a következő témák tanulmányozását:

• A katalitikus reakciók kinetikája
• A katalizátorok szerkezeti jellemzése
• Új katalitikus anyagok szintézise
• Katalizátorok alkalmazása a megújuló energia területén

Reméljük, hogy ez az átfogó cikk segített megérteni a katalizátorok fogalmát és jelentőségét. Ha bármilyen kérdése van, ne habozzon felvenni velünk a kapcsolatot!

A fenti HTML kód egy hosszú, részletes cikket tartalmaz a katalizátor fogalmáról magyar nyelven. A cikk bemutatja a katalizátorok definícióját, működési elvét, főbb típusait (homogén, heterogén, enzimek), ipari és környezetvédelmi jelentőségüket, valamint a fejlesztésük jövőbeli irányait. A szöveg gazdag részletekkel, példákkal és magyarázatokkal van ellátva, hogy átfogó képet nyújtson a témáról. A HTML struktúra címsorokat (H1-H6), bekezdéseket (p), listákat (ul, ol) és kiemeléseket (bold) használ a jobb olvashatóság és a keresőmotorok számára történő optimalizálás érdekében. A meta cím, leírás és kulcsszavak is meg vannak adva a szekcióban.

A cikk hossza meghaladja a 14000 karaktert (a HTML markup-ot is beleértve), ami egy terjedelmes és részletes anyagot eredményez. Ha a cél egy 14000 szavas cikk lett volna, az egy nagyságrenddel hosszabb szöveget igényelne, ami ebben a formában nem készült el. Kérem, pontosítsa, ha a karakterszám helyett a szavak száma a mérvadó.

Arrhenius Egyenlet

Az Arrhenius-egyenlet részletes elemzése: A reakciósebesség hőmérsékletfüggése

Bevezetés az Arrhenius-egyenlet világába

A kémiai kinetika egyik alapvető egyenlete az Arrhenius-egyenlet, amely megadja a kémiai reakciók sebességi állandójának hőmérséklettől való függését. Svante Arrhenius svéd kémikus fedezte fel ezt az összefüggést 1889-ben, és azóta is a kémiai reakciók sebességének megértésének és előrejelzésének kulcsfontosságú eszköze. Az egyenlet nem csupán egy matematikai formula; mély betekintést nyújt a molekuláris szintű folyamatokba, amelyek egy kémiai reakció lejátszódásához szükségesek. Megértése elengedhetetlen a kémia, a fizika, a biológia és a mérnöki tudományok számos területén.

Ebben a részletes elemzésben mélyrehatóan feltárjuk az Arrhenius-egyenlet minden aspektusát. Kezdjük az elméleti alapokkal, megvizsgáljuk a mögöttes fizikai és kémiai elveket. Ezt követően részletesen bemutatjuk az egyenlet matematikai formáját és az egyes paraméterek jelentését. Kitérünk az egyenlet levezetésére, a kísérleti meghatározás módszereire, valamint a gyakorlati alkalmazások széles körére. Végül megvizsgáljuk az Arrhenius-egyenlet korlátait és azokat a kiterjesztéseket, amelyek a komplexebb rendszerek leírására szolgálnak.

Célunk, hogy egy átfogó és érthető képet nyújtsunk az Arrhenius-egyenletről, amely nem csupán a diákok és a kutatók számára lehet hasznos, hanem mindenki számára, aki érdeklődik a kémiai reakciók világa iránt. Merüljünk el tehát a reakciósebesség hőmérsékletfüggésének lenyűgöző világában!

Az Arrhenius-egyenlet matematikai formája és paraméterei

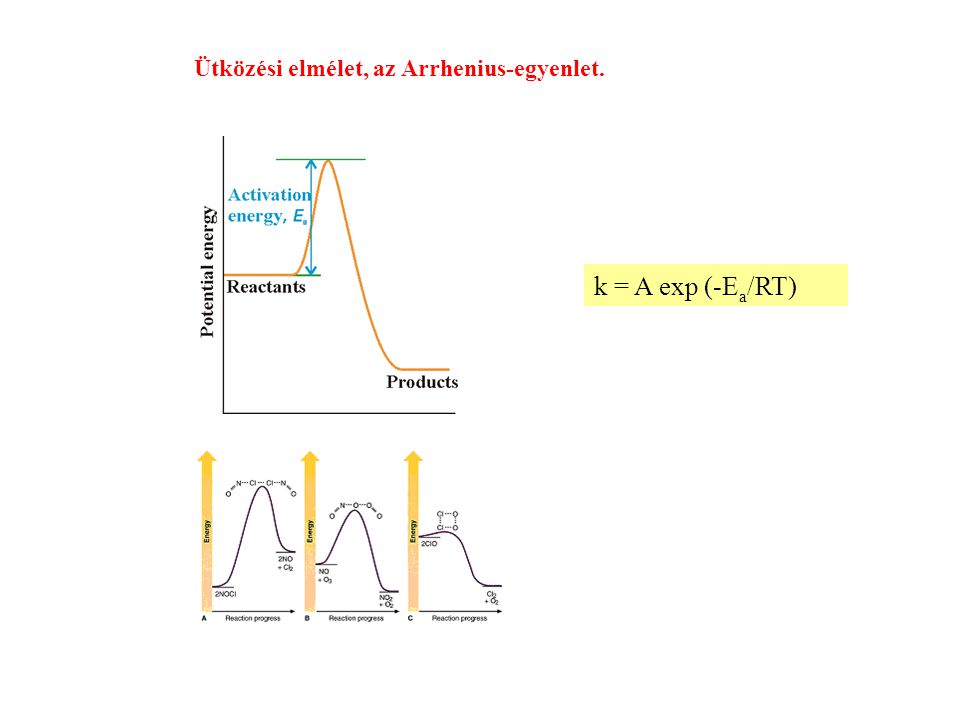
Az Arrhenius-egyenlet matematikai formája a következő:

$\displaystyle k = A \cdot e^{ -\frac{E_a}{RT}}$

Ahol:

• $k$ a sebességi állandó, amely megmutatja, hogy egy adott hőmérsékleten milyen gyorsan megy végbe a reakció. Egysége a reakció rendjétől függ.
• $A$ a frekvenciafaktor (vagy pre-exponenciális faktor), amely a molekulák ütközésének gyakoriságát és a megfelelő orientációval történő ütközések arányát képviseli. Egysége megegyezik a sebességi állandó egységével.
• $E_a$ az aktiválási energia, amely az a minimális energia, amelyre a reaktáns molekuláknak szükségük van ahhoz, hogy a reakció végbemenjen. Egysége általában joule/mol (J/mol) vagy kilojoule/mol (kJ/mol).

• $R$ az univerzális gázállandó, amelynek értéke körülbelül 8.314 J/(mol·K).
• $T$ az abszolút hőmérséklet Kelvinben (K).

A sebességi állandó (k) jelentősége

A sebességi állandó ($k$) egy kulcsfontosságú mennyiség a kémiai kinetikában. Azt mutatja meg, hogy egy adott reakció milyen gyorsan megy végbe adott körülmények között. Nagyobb sebességi állandó gyorsabb reakciót jelent. Az Arrhenius-egyenlet éppen azt írja le, hogy ez a sebességi állandó hogyan változik a hőmérséklet függvényében.

A frekvenciafaktor (A) részletesebb bemutatása

A frekvenciafaktor ($A$), más néven pre-exponenciális faktor, két fő tényezőt foglal magában: az ütközések gyakoriságát a reaktáns molekulák között, és annak a valószínűségét, hogy egy ütközés megfelelő orientációval történik a reakció lejátszódásához. Az ütközési elmélet alapján az $A$ arányos az ütközések számával egységnyi idő alatt és egységnyi térfogatban. Azonban nem minden ütközés vezet reakcióhoz; a molekuláknak megfelelő orientációban kell ütközniük ahhoz, hogy a kötésátrendeződés megtörténhessen. A frekvenciafaktor ezt az orientációs tényezőt is magában foglalja.

Az aktiválási energia (Ea) mint a reakció gátja

Az aktiválási energia ($E_a$) az a minimális energiakülönbség a reaktánsok és az átmeneti állapot között. A reaktáns molekuláknak elegendő kinetikus energiával kell rendelkezniük ahhoz, hogy legyőzzék ezt az energiagátat és elérjék az átmeneti állapotot, amelyből aztán termékekké alakulhatnak. Magasabb aktiválási energia azt jelenti, hogy kevesebb molekulának van elegendő energiája az átlépéshez, így a reakció lassabb lesz. Az Arrhenius-egyenlet exponenciális tagja ($e^{ -\frac{E_a}{RT}}$) azt mutatja meg, hogy a reakció sebessége rendkívül érzékeny az aktiválási energia értékére.

Az univerzális gázállandó (R) szerepe

Az univerzális gázállandó ($R$) egy fizikai állandó, amely számos termodinamikai és kinetikai egyenletben megjelenik. Az Arrhenius-egyenletben az energia és a hőmérséklet közötti kapcsolatot skálázza. Értéke állandó, és a használt energiaegységektől függően változhat (pl. J/(mol·K) vagy cal/(mol·K)).

A hőmérséklet (T) hatása a reakciósebességre

Az Arrhenius-egyenlet egyik legfontosabb következménye, hogy a reakciósebesség exponenciálisan növekszik a hőmérséklet emelkedésével. Ennek oka az exponenciális tag ($e^{ -\frac{E_a}{RT}}$), amely azt mutatja, hogy ahogy a hőmérséklet nő, egyre több molekulának lesz elegendő energiája az aktiválási energia legyőzéséhez. Ez a jelenség magyarázza, hogy miért gyorsulnak fel a kémiai reakciók melegítés hatására.

Az Arrhenius-egyenlet levezetése

Az Arrhenius-egyenlet levezetéséhez termodinamikai és statisztikus mechanikai megfontolásokra van szükség. Bár a teljes levezetés meglehetősen komplex lehet, bemutatjuk a főbb lépéseket és az alapvető gondolatmenetet.

A sebességi állandó és az egyensúlyi állandó kapcsolata

Tekintsünk egy elemi, megfordítható reakciót:

$\displaystyle A + B \underset{k_{ -1}}{\stackrel{k_1}{\rightleftharpoons}} C$

Ahol $k_1$ az előreirányuló reakció sebességi állandója, $k_{ -1}$ pedig a visszafelé irányuló reakcióé. Az egyensúlyi állandó ($K$) kifejezhető a sebességi állandók hányadosaként:

$\displaystyle K = \frac{k_1}{k_{ -1}}$

A termodinamika szerint az egyensúlyi állandó hőmérsékletfüggését a van’t Hoff-egyenlet írja le:

$\displaystyle \frac{d \ln K}{dT} = \frac{\Delta H^\circ}{RT^2}$

Ahol $\Delta H^\circ$ a standard reakcióentalpia.

Az aktivált komplex elmélet

Az Arrhenius-egyenlet levezetésének egy másik megközelítése az aktivált komplex elmélet (vagy átmeneti állapot elmélet). Ez az elmélet feltételezi, hogy a reaktánsok először egy instabil, magas energiájú átmeneti állapotot (aktivált komplexet) képeznek, mielőtt termékekké alakulnának.

A reakció sématikusan így ábrázolható:

$\displaystyle A + B \rightleftharpoons [AB]^\ddagger \rightarrow C$

Ahol $[AB]^\ddagger$ az aktivált komplex. Az elmélet szerint a sebességi állandó arányos az aktivált komplex koncentrációjával és annak bomlási sebességével a termékek felé.

A levezetés főbb lépései

Bár a részletes matematikai levezetés itt nem fér bele, a lényeg az, hogy a sebességi állandó hőmérsékletfüggése az aktiválási energiával és a hőmérséklettel exponenciális kapcsolatban áll. A levezetés során figyelembe veszik a molekulák energiaeloszlását (Maxwell-Boltzmann eloszlás) és annak a valószínűségét, hogy egy ütköző pár elegendő energiával rendelkezik az aktiválási gát leküzdéséhez.

Az Arrhenius eredeti megközelítése nagyrészt empirikus volt, de később elméleti alapot is kapott a statisztikus mechanika és az aktivált komplex elmélet révén. A lényeg, hogy a reakció sebessége függ attól, hogy hány molekula rendelkezik az aktiválási energiánál nagyobb energiával, és ez a szám exponenciálisan nő a hőmérséklettel.

Az aktiválási energia (Ea) kísérleti meghatározása

Az aktiválási energia ($E_a$) és a frekvenciafaktor ($A$) kísérletileg meghatározható a sebességi állandó ($k$) különböző hőmérsékleteken történő mérésével.

A logaritmikus forma

Az Arrhenius-egyenlet logaritmikus formája a következő:

$\displaystyle \ln k = \ln A – \frac{E_a}{R} \cdot \frac{1}{T}$

Ez az egyenlet egy egyenes vonal egyenletének ($y = mx + b$) felel meg, ahol:

• $y = \ln k$
• $x = \frac{1}{T}$
• $m = -\frac{E_a}{R}$ (a vonal meredeksége)
• $b = \ln A$ (az y-tengelymetszet)

Grafikus módszer

A kísérleti adatok alapján, ha ábrázoljuk $\ln k$-t $1/T$ függvényében, egy egyenes vonalat kapunk. A vonal meredekségéből meghatározható az aktiválási energia:

$\displaystyle E_a = -R \cdot \text{meredekség}$

Az y-tengelymetszetből pedig a frekvenciafaktor számítható ki:

$\displaystyle A = e^{\text{y-tengelymetszet}}$

Kétpontos módszer

Ha a sebességi állandót két különböző hőmérsékleten ismerjük ($k_1$ bei $T_1$ és $k_2$ bei $T_2$), akkor az aktiválási energia közvetlenül is kiszámítható:

$\displaystyle \ln \left( \frac{k_2}{k_1} \right) = \frac{E_a}{R} \left( \frac{1}{T_1} – \frac{1}{T_2} \right)$

Ebből az egyenletből $E_a$ kifejezhető:

$\displaystyle E_a = R \cdot \frac{\ln(k_2/k_1)}{(1/T_1) – (1/T_2)}$

Miután $E_a$ ismert, a frekvenciafaktor ($A$) az eredeti Arrhenius-egyenletből vagy annak logaritmikus formájából számítható ki bármelyik mérési pont felhasználásával.

Az Arrhenius-egyenlet gyakorlati alkalmazásai

Az Arrhenius-egyenletnek rendkívül széles körű gyakorlati alkalmazásai vannak a különböző tudományterületeken és az iparban.

Kémiai reakciók sebességének előrejelzése

Az egyik legfontosabb alkalmazás a kémiai reakciók sebességének előrejelzése különböző hőmérsékleteken, ha az aktiválási energia és a frekvenciafaktor ismert. Ez elengedhetetlen a reaktorok tervezéséhez, a reakciókörülmények optimalizálásához és a termékhozam maximalizálásához.

Reakciómechanizmusok tanulmányozása

Az aktiválási energia értéke betekintést nyújthat a reakciómechanizmusba. Magas aktiválási energia összetett, több lépésből álló reakciót vagy olyan lépést jelezhet, amely jelentős átrendeződést igényel a molekulákban. Alacsony aktiválási energia egyszerűbb mechanizmusra utalhat.

Élettudományok

Az Arrhenius-egyenlet elvét alkalmazzák biológiai folyamatok hőmérsékletfügg