Elsrend Reakcio

Az Elsrendű Reakciók Átfogó Tanulmánya: A Kémiai Kinetika Alapjai

A kémiai kinetika a kémiai reakciók sebességével és mechanizmusával foglalkozó tudományterület. Ezen a területen belül az elsrendű reakciók különleges jelentőséggel bírnak egyszerűségük és gyakori előfordulásuk miatt. Ebben a részletes útmutatóban mélyrehatóan megvizsgáljuk az elsrendű reakciók jellemzőit, matematikai leírását, példáit és gyakorlati alkalmazásait.

Mi az az Elsrendű Reakció? Definíció és Alapelvek

Egy kémiai reakció akkor elsrendű, ha a reakciósebesség egyetlen reaktáns koncentrációjával egyenesen arányos. Ez azt jelenti, hogy ha megduplázzuk ennek a reaktánsnak a koncentrációját, a reakció sebessége is kétszeresére nő. Az elsrendű reakciókban a reakciósebesség nem függ más reaktánsok koncentrációjától (ha vannak ilyenek), vagyis a reakció sebessége kizárólag egyetlen komponens mennyiségétől függ.

Az Elsrendű Reakciók Sebességi Törvénye

Az elsrendű reakciók sebességi törvénye matematikailag a következőképpen fejezhető ki:

$$\text{sebesség} = -\frac{d[A]}{dt} = k[A]$$

ahol:

• $-\frac{d[A]}{dt}$ a reaktáns A koncentrációjának időbeli változási sebessége (a negatív előjel azt jelzi, hogy a reaktáns koncentrációja csökken az idővel).
• $[A]$ a reaktáns A pillanatnyi koncentrációja.
• $k$ a sebességi állandó, amely az adott reakcióra és hőmérsékletre jellemző. Mértékegysége $s^{ -1}$.

Az Integrált Sebességi Törvény Elsrendű Reakciókra

A sebességi törvény integrálásával megkaphatjuk az integrált sebességi törvényt, amely megmutatja, hogyan változik a reaktáns koncentrációja az idő függvényében. Elsrendű reakciókra az integrált sebességi törvény a következő:

$$\ln[A]_t – \ln[A]_0 = -kt$$

vagy átrendezve:

$$[A]_t = [A]_0 e^{ -kt}$$

ahol:

• $[A]_t$ a reaktáns A koncentrációja a $t$ időpillanatban.
• $[A]_0$ a reaktáns A kezdeti koncentrációja ($t=0$-kor).
• $k$ a sebességi állandó.
• $t$ az eltelt idő.

Ez az egyenlet lineáris formában is felírható, ha a $\ln[A]_t$-t ábrázoljuk az idő függvényében. Ekkor egy negatív meredekségű ($k$) egyenest kapunk, amelynek y-tengelymetszete $\ln[A]_0$.

Az Elsrendű Reakciók Felezési Ideje

A felezési idő ($t_{1/2}$) az az idő, amely alatt egy reaktáns koncentrációja a kezdeti értékének a felére csökken. Elsrendű reakciókra a felezési idő független a kezdeti koncentrációtól, és a következőképpen számítható ki:

$$t_{1/2} = \frac{\ln(2)}{k} \approx \frac{0.693}{k}$$

Ez a tulajdonság rendkívül hasznos az elsrendű folyamatok, például a radioaktív bomlás sebességének jellemzésére.

Példák Elsrendű Reakciókra a Kémiában és a Természetben

Számos fontos kémiai és fizikai folyamat követ elsrendű kinetikát.

Radioaktív Bomlás

A radioaktív bomlás egy klasszikus példa az elsrendű reakcióra. Egy adott radioaktív izotóp bomlásának sebessége arányos a jelenlévő izotóp mennyiségével. Például a szén-14 bomlása nitrogén-14-re egy elsrendű folyamat, amelyet a radiokarbon kormeghatározásban használnak.

A szén-14 bomlásának sebességi törvénye:

$$\text{sebesség} = -\frac{d[^{14}C]}{dt} = k[^{14}C]$$

A szén-14 felezési ideje körülbelül 5730 év.

Unimolekuláris Izomerizációk

Egyes molekuláris izomerizációs reakciók is elsrendű kinetikát követhetnek. Ilyenkor egyetlen molekula alakul át egy másik izomerré anélkül, hogy más molekulákkal ütközne a sebességmeghatározó lépésben. Például a ciklobután butadiénné történő izomerizációja magas hőmérsékleten elsrendű reakció.

Gázfázisú Bomlások

Bizonyos gázfázisú molekulák bomlása is elsrendű lehet, különösen alacsony nyomáson, ahol a molekulák közötti ütközések ritkák. Ilyenkor a sebességmeghatározó lépés egyetlen molekula aktivációja.

Enzim által katalizált reakciók alacsony szubsztrátkoncentráció mellett

Bár az enzim által katalizált reakciók általában bonyolultabb kinetikát követnek (Michaelis-Menten kinetika), nagyon alacsony szubsztrátkoncentrációk mellett a reakció sebessége megközelítőleg arányos lehet a szubsztrát koncentrációjával, így ilyen körülmények között elsrendűnek tekinthető.

Az Elsrendű Reakciók Grafikus Ábrázolása

Az elsrendű reakciók kinetikájának megértéséhez elengedhetetlen a koncentráció időbeli változásának grafikus ábrázolása.

Koncentráció-Idő Grafikon

Ha egy elsrendű reakcióban a reaktáns koncentrációját ábrázoljuk az idő függvényében, egy exponenciálisan csökkenő görbét kapunk. Ez a görbe tükrözi az $[A]_t = [A]_0 e^{ -kt}$ egyenletet.

Ln[A]-Idő Grafikon

Ahogy korábban említettük, ha az elsrendű reakcióban a reaktáns koncentrációjának természetes logaritmusát ($\ln[A]_t$) ábrázoljuk az idő függvényében, egy egyenes vonalat kapunk. Ennek az egyenesnek a meredeksége $-k$, a y-tengelymetszete pedig $\ln[A]_0$. Ez a grafikon nagyon hasznos annak megállapítására, hogy egy adott reakció elsrendű-e, és a sebességi állandó ($k$) meghatározására.

A Sebességi Állandót Befolyásoló Tényezők

A sebességi állandó ($k$) nem egy állandó minden körülmények között. Értékét befolyásolja néhány kulcsfontosságú tényező.

Hőmérséklet Hatása: Az Arrhenius-egyenlet

A hőmérséklet jelentősen befolyásolja a reakciósebességet, és így a sebességi állandót is. Általánosságban elmondható, hogy a hőmérséklet növelésével a reakciósebesség nő. Ezt a kapcsolatot az Arrhenius-egyenlet írja le:

$$k = A e^{ -E_a/RT}$$

ahol:

• $k$ a sebességi állandó.
• $A$ a pre-exponenciális faktor vagy frekvenciafaktor, amely a molekulák ütközésének gyakoriságával és orientációjával kapcsolatos.
• $E_a$ az aktiválási energia, amely a reakció beindulásához szükséges minimális energia.
• $R$ az univerzális gázállandó.
• $T$ az abszolút hőmérséklet (Kelvinben).

Az Arrhenius-egyenlet logaritmikus formája:

$$\ln(k) = \ln(A) – \frac{E_a}{R} \frac{1}{T}$$

Ha $\ln(k)$-t ábrázoljuk $1/T$ függvényében, egy egyenes vonalat kapunk, amelynek meredeksége $-E_a/R$, és y-tengelymetszete $\ln(A)$. Ezzel a módszerrel kísérleti adatokból meghatározható az aktiválási energia.

Katalizátorok Hatása

A katalizátorok olyan anyagok, amelyek megnövelik a reakciósebességet anélkül, hogy maguk elfogynának a reakció során. A katalizátorok úgy működnek, hogy egy alternatív reakcióutat biztosítanak alacsonyabb aktiválási energiával. Bár a katalizátorok megváltoztatják a reakció sebességét, nem befolyásolják a reakció rendjét (azaz, ha egy reakció eredetileg elsrendű volt, katalizátor jelenlétében is az marad), de megváltoztatják a sebességi állandó értékét.

Elsrendű Reakciók Mechanizmusai

Az elsrendű kinetika gyakran egy elemi lépést tükröz a reakciómechanizmusban, amelyben egyetlen molekula vesz részt a sebességmeghatározó lépésben. Azonban egy összetett reakció is mutathat elsrendű kinetikát bizonyos körülmények között.

Unimolekuláris Elemi Lépések

Ha a reakciómechanizmus egyetlen sebességmeghatározó lépést tartalmaz, amelyben egyetlen molekula alakul át, akkor a teljes reakció elsrendű kinetikát fog mutatni. Például egy molekula izomerizációja vagy bomlása, ha ez a lépés a leglassabb a sorozatban.

Pszeudo-Elsrendű Reakciók

Előfordulhat, hogy egy reakció valójában nem elsrendű, de bizonyos kísérleti körülmények között úgy viselkedik, mintha az lenne. Ezt pszeudo-elsrendű reakciónak nevezzük. Ez akkor következik be, ha egy vagy több reaktáns koncentrációja sokkal nagyobb, mint a többié, így ezeknek a koncentrációknak a változása a reakció során elhanyagolható. Ebben az esetben a sebességi törvény leegyszerűsödik, és úgy tűnik, mintha csak egyetlen reaktáns koncentrációjától függne.

Például, ha egy reakció sebességi törvénye $\text{sebesség} = k[A][B]$, és $[B]$ sokkal nagyobb, mint $[A]$, akkor $[B]$ gyakorlatilag állandónak tekinthető, és a sebességi törvény átírható $\text{sebesség} = (k[B])[A] = k'[A]$ formában, ahol $k’ = k[B]$ egy pszeudo-elsrendű sebességi állandó.

Alkalmazások: Hol Találkozunk Elsrendű Reakciókkal?

Az elsrendű reakciók megértése számos tudományterületen és gyakorlati alkalmazásban kulcsfontosságú.

Radiokarbon Kormeghatározás

Mint korábban említettük, a radiokarbon kormeghatározás az egyik legfontosabb alkalmazása az elsrendű kinetikának. A szén-14 radioaktív bomlása elsrendű folyamat, ismert felezési idővel. A régészeti leletekben található szén-14 és a stabil szén-12 arányának mérésével meg lehet határozni a lelet korát.

Gyógyszerkinetika

A gyógyszerkinetikában gyakran feltételezik, hogy a gyógyszerek eliminációja a szervezetből (például metabolizmus vagy kiválasztás útján) elsrendű kinetikát követ. Ez azt jelenti, hogy a gyógyszer koncentrációjának időbeli csökkenése arányos a pillanatnyi koncentrációval. Ez a modell segít a gyógyszerek adagolásának és hatásának megtervezésében.

Nukleáris Reaktorok

A nukleáris reaktorokban a radioaktív elemek bomlása, amely sok esetben elsrendű kinetikát követ, fontos szerepet játszik a hőtermelésben és a reaktor működésének szabályozásában.

Kémiai Analízis

Bizonyos kémiai analitikai módszerek, például a bomláson alapuló titrálások, az elsrendű kinetika elvén működhetnek a vizsgált anyag mennyiségének meghatározására.

Összefoglalás: Az Elsrendű Reakciók Fontossága

Az elsrendű reakciók a kémiai kinetika alapvető építőkövei. Egyszerű matematikai leírásuk és számos természeti és mesterséges folyamatban való előfordulásuk miatt kiemelkedő jelentőséggel bírnak. A sebességi törvény, az integrált sebességi törvény és a felezési idő fogalmainak megértése elengedhetetlen a kémiai reakciók sebességének és mechanizmusának tanulmányozásához. A hőmérséklet és a katalizátorok hatásának ismerete tovább mélyíti az elsrendű reakciók viselkedésének megértését és alkalmazásuk lehetőségeit.

További Tanulási Lehetőségek

Ha mélyebben szeretne elmerülni az elsrendű reakciók világában, javasoljuk a következő témák tanulmányozását:

• Másodrendű és nulladrendű reakciók kinetikája.
• Összetett reakciók kinetikája (sorozatos és párhuzamos reakciók).
• Reakciómechanizmusok részletes kidolgozása.
• Kinetikai mérések és adatok analízise.

Reméljük, hogy

Arrhenius Egyenlet

Az Arrhenius-egyenlet részletes elemzése: A reakciósebesség hőmérsékletfüggése

Bevezetés az Arrhenius-egyenlet világába

A kémiai kinetika egyik alapvető egyenlete az Arrhenius-egyenlet, amely megadja a kémiai reakciók sebességi állandójának hőmérséklettől való függését. Svante Arrhenius svéd kémikus fedezte fel ezt az összefüggést 1889-ben, és azóta is a kémiai reakciók sebességének megértésének és előrejelzésének kulcsfontosságú eszköze. Az egyenlet nem csupán egy matematikai formula; mély betekintést nyújt a molekuláris szintű folyamatokba, amelyek egy kémiai reakció lejátszódásához szükségesek. Megértése elengedhetetlen a kémia, a fizika, a biológia és a mérnöki tudományok számos területén.

Ebben a részletes elemzésben mélyrehatóan feltárjuk az Arrhenius-egyenlet minden aspektusát. Kezdjük az elméleti alapokkal, megvizsgáljuk a mögöttes fizikai és kémiai elveket. Ezt követően részletesen bemutatjuk az egyenlet matematikai formáját és az egyes paraméterek jelentését. Kitérünk az egyenlet levezetésére, a kísérleti meghatározás módszereire, valamint a gyakorlati alkalmazások széles körére. Végül megvizsgáljuk az Arrhenius-egyenlet korlátait és azokat a kiterjesztéseket, amelyek a komplexebb rendszerek leírására szolgálnak.

Célunk, hogy egy átfogó és érthető képet nyújtsunk az Arrhenius-egyenletről, amely nem csupán a diákok és a kutatók számára lehet hasznos, hanem mindenki számára, aki érdeklődik a kémiai reakciók világa iránt. Merüljünk el tehát a reakciósebesség hőmérsékletfüggésének lenyűgöző világában!

Az Arrhenius-egyenlet matematikai formája és paraméterei

Az Arrhenius-egyenlet matematikai formája a következő:

$\displaystyle k = A \cdot e^{ -\frac{E_a}{RT}}$

Ahol:

• $k$ a sebességi állandó, amely megmutatja, hogy egy adott hőmérsékleten milyen gyorsan megy végbe a reakció. Egysége a reakció rendjétől függ.
• $A$ a frekvenciafaktor (vagy pre-exponenciális faktor), amely a molekulák ütközésének gyakoriságát és a megfelelő orientációval történő ütközések arányát képviseli. Egysége megegyezik a sebességi állandó egységével.
• $E_a$ az aktiválási energia, amely az a minimális energia, amelyre a reaktáns molekuláknak szükségük van ahhoz, hogy a reakció végbemenjen. Egysége általában joule/mol (J/mol) vagy kilojoule/mol (kJ/mol).

• $R$ az univerzális gázállandó, amelynek értéke körülbelül 8.314 J/(mol·K).
• $T$ az abszolút hőmérséklet Kelvinben (K).

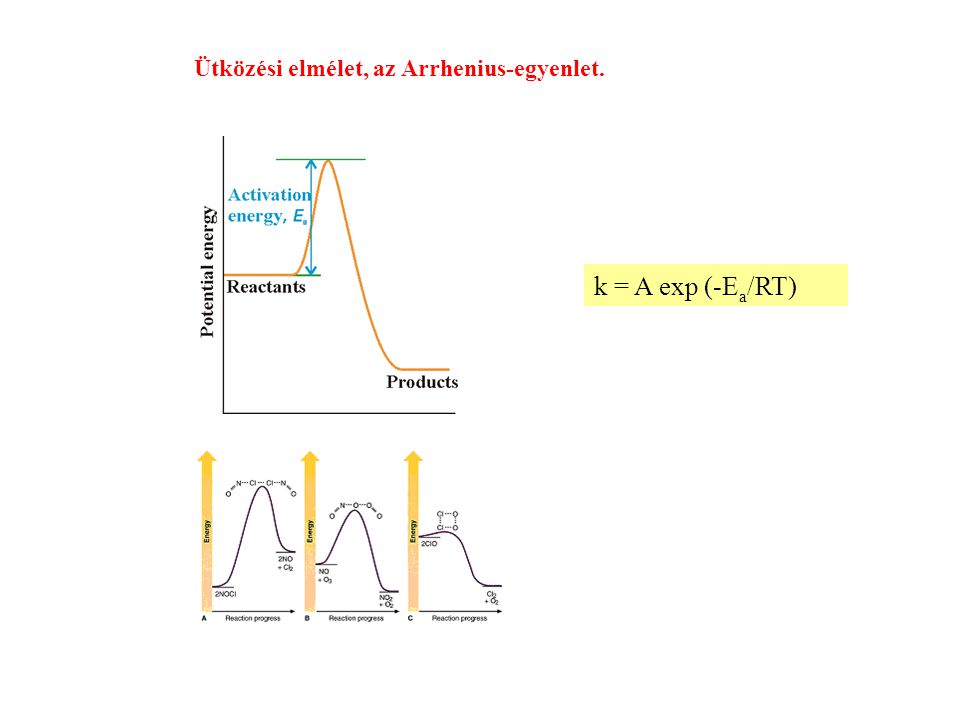
A sebességi állandó (k) jelentősége

A sebességi állandó ($k$) egy kulcsfontosságú mennyiség a kémiai kinetikában. Azt mutatja meg, hogy egy adott reakció milyen gyorsan megy végbe adott körülmények között. Nagyobb sebességi állandó gyorsabb reakciót jelent. Az Arrhenius-egyenlet éppen azt írja le, hogy ez a sebességi állandó hogyan változik a hőmérséklet függvényében.

A frekvenciafaktor (A) részletesebb bemutatása

A frekvenciafaktor ($A$), más néven pre-exponenciális faktor, két fő tényezőt foglal magában: az ütközések gyakoriságát a reaktáns molekulák között, és annak a valószínűségét, hogy egy ütközés megfelelő orientációval történik a reakció lejátszódásához. Az ütközési elmélet alapján az $A$ arányos az ütközések számával egységnyi idő alatt és egységnyi térfogatban. Azonban nem minden ütközés vezet reakcióhoz; a molekuláknak megfelelő orientációban kell ütközniük ahhoz, hogy a kötésátrendeződés megtörténhessen. A frekvenciafaktor ezt az orientációs tényezőt is magában foglalja.

Az aktiválási energia (Ea) mint a reakció gátja

Az aktiválási energia ($E_a$) az a minimális energiakülönbség a reaktánsok és az átmeneti állapot között. A reaktáns molekuláknak elegendő kinetikus energiával kell rendelkezniük ahhoz, hogy legyőzzék ezt az energiagátat és elérjék az átmeneti állapotot, amelyből aztán termékekké alakulhatnak. Magasabb aktiválási energia azt jelenti, hogy kevesebb molekulának van elegendő energiája az átlépéshez, így a reakció lassabb lesz. Az Arrhenius-egyenlet exponenciális tagja ($e^{ -\frac{E_a}{RT}}$) azt mutatja meg, hogy a reakció sebessége rendkívül érzékeny az aktiválási energia értékére.

Az univerzális gázállandó (R) szerepe

Az univerzális gázállandó ($R$) egy fizikai állandó, amely számos termodinamikai és kinetikai egyenletben megjelenik. Az Arrhenius-egyenletben az energia és a hőmérséklet közötti kapcsolatot skálázza. Értéke állandó, és a használt energiaegységektől függően változhat (pl. J/(mol·K) vagy cal/(mol·K)).

A hőmérséklet (T) hatása a reakciósebességre

Az Arrhenius-egyenlet egyik legfontosabb következménye, hogy a reakciósebesség exponenciálisan növekszik a hőmérséklet emelkedésével. Ennek oka az exponenciális tag ($e^{ -\frac{E_a}{RT}}$), amely azt mutatja, hogy ahogy a hőmérséklet nő, egyre több molekulának lesz elegendő energiája az aktiválási energia legyőzéséhez. Ez a jelenség magyarázza, hogy miért gyorsulnak fel a kémiai reakciók melegítés hatására.

Az Arrhenius-egyenlet levezetése

Az Arrhenius-egyenlet levezetéséhez termodinamikai és statisztikus mechanikai megfontolásokra van szükség. Bár a teljes levezetés meglehetősen komplex lehet, bemutatjuk a főbb lépéseket és az alapvető gondolatmenetet.

A sebességi állandó és az egyensúlyi állandó kapcsolata

Tekintsünk egy elemi, megfordítható reakciót:

$\displaystyle A + B \underset{k_{ -1}}{\stackrel{k_1}{\rightleftharpoons}} C$

Ahol $k_1$ az előreirányuló reakció sebességi állandója, $k_{ -1}$ pedig a visszafelé irányuló reakcióé. Az egyensúlyi állandó ($K$) kifejezhető a sebességi állandók hányadosaként:

$\displaystyle K = \frac{k_1}{k_{ -1}}$

A termodinamika szerint az egyensúlyi állandó hőmérsékletfüggését a van’t Hoff-egyenlet írja le:

$\displaystyle \frac{d \ln K}{dT} = \frac{\Delta H^\circ}{RT^2}$

Ahol $\Delta H^\circ$ a standard reakcióentalpia.

Az aktivált komplex elmélet

Az Arrhenius-egyenlet levezetésének egy másik megközelítése az aktivált komplex elmélet (vagy átmeneti állapot elmélet). Ez az elmélet feltételezi, hogy a reaktánsok először egy instabil, magas energiájú átmeneti állapotot (aktivált komplexet) képeznek, mielőtt termékekké alakulnának.

A reakció sématikusan így ábrázolható:

$\displaystyle A + B \rightleftharpoons [AB]^\ddagger \rightarrow C$

Ahol $[AB]^\ddagger$ az aktivált komplex. Az elmélet szerint a sebességi állandó arányos az aktivált komplex koncentrációjával és annak bomlási sebességével a termékek felé.

A levezetés főbb lépései

Bár a részletes matematikai levezetés itt nem fér bele, a lényeg az, hogy a sebességi állandó hőmérsékletfüggése az aktiválási energiával és a hőmérséklettel exponenciális kapcsolatban áll. A levezetés során figyelembe veszik a molekulák energiaeloszlását (Maxwell-Boltzmann eloszlás) és annak a valószínűségét, hogy egy ütköző pár elegendő energiával rendelkezik az aktiválási gát leküzdéséhez.

Az Arrhenius eredeti megközelítése nagyrészt empirikus volt, de később elméleti alapot is kapott a statisztikus mechanika és az aktivált komplex elmélet révén. A lényeg, hogy a reakció sebessége függ attól, hogy hány molekula rendelkezik az aktiválási energiánál nagyobb energiával, és ez a szám exponenciálisan nő a hőmérséklettel.

Az aktiválási energia (Ea) kísérleti meghatározása

Az aktiválási energia ($E_a$) és a frekvenciafaktor ($A$) kísérletileg meghatározható a sebességi állandó ($k$) különböző hőmérsékleteken történő mérésével.

A logaritmikus forma

Az Arrhenius-egyenlet logaritmikus formája a következő:

$\displaystyle \ln k = \ln A – \frac{E_a}{R} \cdot \frac{1}{T}$

Ez az egyenlet egy egyenes vonal egyenletének ($y = mx + b$) felel meg, ahol:

• $y = \ln k$
• $x = \frac{1}{T}$
• $m = -\frac{E_a}{R}$ (a vonal meredeksége)
• $b = \ln A$ (az y-tengelymetszet)

Grafikus módszer

A kísérleti adatok alapján, ha ábrázoljuk $\ln k$-t $1/T$ függvényében, egy egyenes vonalat kapunk. A vonal meredekségéből meghatározható az aktiválási energia:

$\displaystyle E_a = -R \cdot \text{meredekség}$

Az y-tengelymetszetből pedig a frekvenciafaktor számítható ki:

$\displaystyle A = e^{\text{y-tengelymetszet}}$

Kétpontos módszer

Ha a sebességi állandót két különböző hőmérsékleten ismerjük ($k_1$ bei $T_1$ és $k_2$ bei $T_2$), akkor az aktiválási energia közvetlenül is kiszámítható:

$\displaystyle \ln \left( \frac{k_2}{k_1} \right) = \frac{E_a}{R} \left( \frac{1}{T_1} – \frac{1}{T_2} \right)$

Ebből az egyenletből $E_a$ kifejezhető:

$\displaystyle E_a = R \cdot \frac{\ln(k_2/k_1)}{(1/T_1) – (1/T_2)}$

Miután $E_a$ ismert, a frekvenciafaktor ($A$) az eredeti Arrhenius-egyenletből vagy annak logaritmikus formájából számítható ki bármelyik mérési pont felhasználásával.

Az Arrhenius-egyenlet gyakorlati alkalmazásai

Az Arrhenius-egyenletnek rendkívül széles körű gyakorlati alkalmazásai vannak a különböző tudományterületeken és az iparban.

Kémiai reakciók sebességének előrejelzése

Az egyik legfontosabb alkalmazás a kémiai reakciók sebességének előrejelzése különböző hőmérsékleteken, ha az aktiválási energia és a frekvenciafaktor ismert. Ez elengedhetetlen a reaktorok tervezéséhez, a reakciókörülmények optimalizálásához és a termékhozam maximalizálásához.

Reakciómechanizmusok tanulmányozása

Az aktiválási energia értéke betekintést nyújthat a reakciómechanizmusba. Magas aktiválási energia összetett, több lépésből álló reakciót vagy olyan lépést jelezhet, amely jelentős átrendeződést igényel a molekulákban. Alacsony aktiválási energia egyszerűbb mechanizmusra utalhat.

Élettudományok

Az Arrhenius-egyenlet elvét alkalmazzák biológiai folyamatok hőmérsékletfügg